索赔额服从指数分布的聚合模型条件风险价值研究

杜 燕,彭可歌

根据市场特点和投资理论,条件风险价值(Conditional Value-at-Risk,CVaR)在度量短期模型的风险大小中有重要作用[1,2].2003年,Landsma等给出了基于总理赔额正态近似分布的CVaR的计算结果[3].个别索赔额服从指数分布是一类重要的保险模型,在个别风险模型中,总理赔额服从伽马分布.2005年,Landsma等给出了伽马分布的CVaR计算结果[4].笔者通过卷积法计算聚合风险模型中总理赔额,进而得到聚合风险模型的CVaR的计算公式.

定义1[5]损失变量L在置信水平α下的风险价值(Value-at-Risk,VaR)为

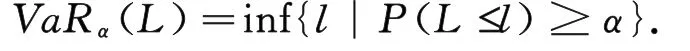
定义2[6]损失变量L在置信水平α下的条件风险价值(CVa R)为

引理[7]损失变量L的分布函数为FL(x),有,其中πα为FL(x)的α分位点.

定理 在短期聚合风险模型中,若个体索赔额服从均值为θ的指数分布,理赔次数,则总理赔额S在置信水平α下的CVa R为

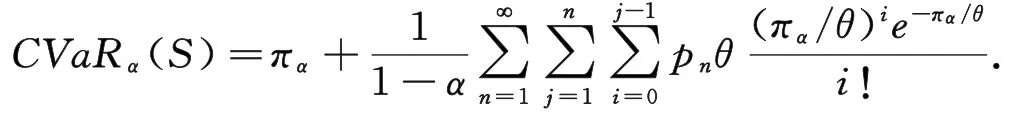
证 根据卷积方法,由全概率公式

其中F*n(x)为个别索赔额X的n重卷积分布函数.

N=n时,X1,X2,...,Xn服从,由伽马分布的可加性,X1+X2+...+Xn的分布为,即X1+X2+...+Xn的分布函数为

根据式(1)、(2),有

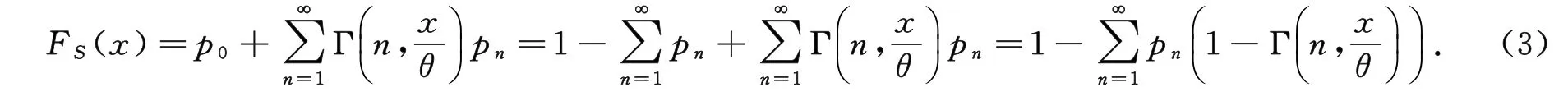
根据伽马函数的性质[8],

下面计算积分

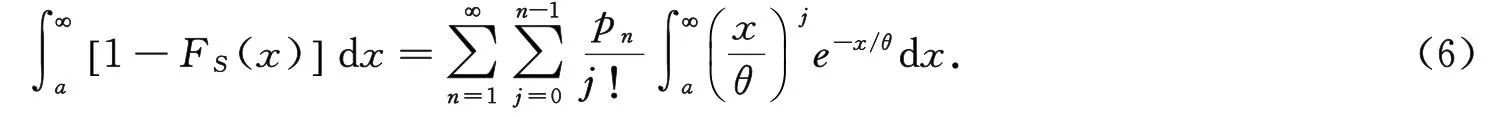
记

有

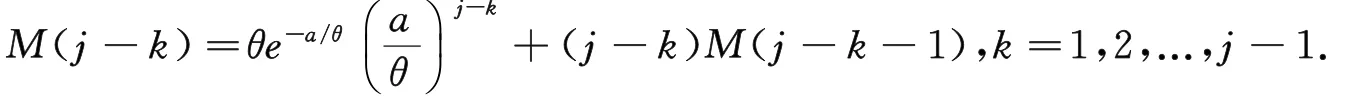
将式(8)代入式(9)得到

又根据伽马函数的性质

将式(11)代入式(9)得

将式(12)代入式(6)得

而根据引理,有

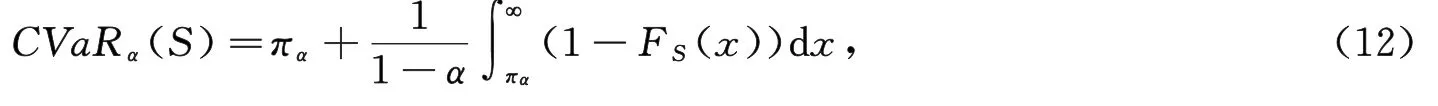
将式(13)代入式(12)得

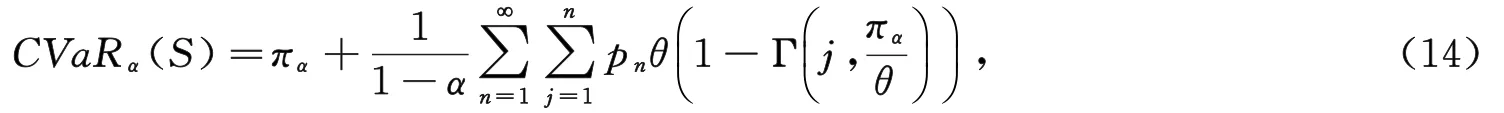
其中,πα为FS(x)的α分位点,根据式(14)和式(5),有

参考文献:

[1]黎子良,邢海鹏.金融市场中的统计模型和方法[M].北京:高等教育出版社,2009.

[2]Hans Follmer,Alexander Schied.Stochastic Finance:An Introduction in Discrete Time[M].Berlin:Walter de Gruyter,2004:177-183.

[3]Landsman Z,Valdez E.Tail Conditional Expectations for Elliptical Distributions[J].North American Actuarial Journal,2003,7(4):55-71.

[4]Landsman Z,Valdez E.Tail Conditional Expectations for Exponential Dispersion Models[J].ASTIN Bulletin,2005,35(1):189-209.

[5]Artzner P,Delhaen F,Eber M,et al.Coherent measures of risk[J].Mathematical Finance,1999(9):203-208.

[6]Acerbi C,Tasche D.On the coherence of expected shortfall[J].Journal of Banking and Finance,2002,26(7):1487-1503.

[7]肖争艳.精算模型[M].北京:中国人民大学出版社,2013.

[8]Stuart A K,Harry H P,Gordon W.Loss Models:From Data to Decisions[M].New Jersey:John Wiley&Sons,1998:84-86.