一类新的预条件SOR迭代法

高树玲,赵苗婵

讨论线性方程组

其中A=(aij)∈Rn×n非奇异,X,b∈Rn.

不失一般性,假定A的对角线元素全是1,设A=I-L-U,其中L和U分别为A的严格下三角和严格上三角矩阵.

考虑预条件系统PAX=Pb,其中P∈Rn×n为非奇异矩阵.常见的预条件矩阵有P=I+S和P=I+R.其中

I是单位矩阵,aij是矩阵(aij)n×n对应位置上的元素.另外还有其他的一些预条件矩阵.本文考虑一种新的预条件因子

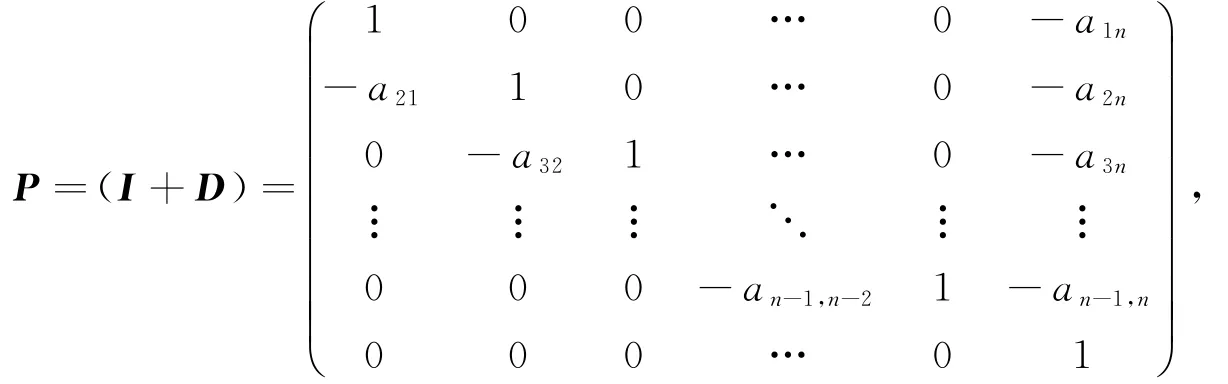
在一定条件下该预条件SOR迭代法为收敛的.古典和该预条件后SOR迭代矩阵分别记为Lω,～Lω.令

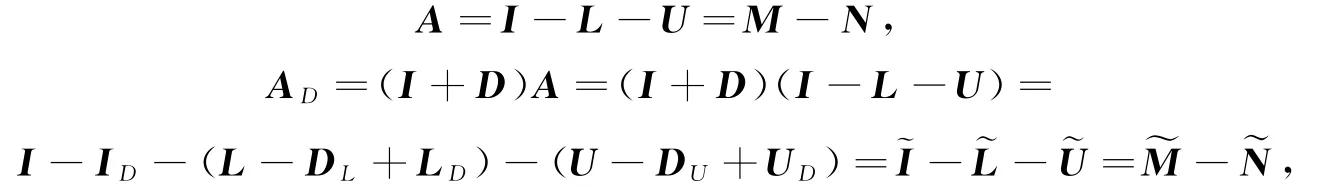
D的严格下和上三角阵,ID,LD,UD分别表示D(L+U)的对角阵和严格下和上三角阵.则

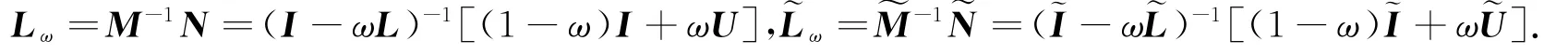
1 相关的定义和引理

定义1[1]设A=(aij)∈Rn×n.若A可表示为A=s I-B,其中B≥0,则当s＞ρ(B)时,称A为非奇异的M-矩阵,简称M-矩阵;若A满足aij≤0(1≤i≠j≤n),aii＞0(i=1,2,…,n),则称A为L矩阵.其中ρ(B)为矩阵B的谱半径.

定义2[2]若M是非奇异n阶矩阵,称A=M-N是A的分裂,若ρ(M-1N)＜1,则称分裂A=M-N是收敛的;若M-1≥0,N≥0,则称分裂A=M-N是正规的;若M-1≥0,M-1N＞0,则称分裂A=M-N是弱正规的.

定义3[2]如果一个n×n矩阵A=(aij)满足:i≠j时,aij≤0,A是非奇异的且A-1≥0,则称A为非奇异的Z-阵.

引理1[2]设A=M-N是A的正规或弱正规分裂,则ρ(M-1N)＜1的充要条件为A-1≥0.

引理2[3]如果A为非负不可约矩阵,则:

1)ρ(A)为A的一正的特征值;

2)A有一正的特征向量x与ρ(A)相对应;

3)A的任意元素增加时ρ(A)也增加.

引理3[4]设A=M1-N1=M2-N2是A的两个弱正规分裂,如果A-1≥0,并且下列条件之一成立:

1)N1≤N2;2)M-11≥M-12,N1≥0;3)M-11≥M-12,N2≥0;

引理4[5]若A是非负矩阵,则:

1)若αx≤Ax对某一非负向量x且x≠0成立,则α≤ρ(A);

2)若Ax≤βx对某一正向量x成立,则ρ(A)≤β,进一步,如果A是不可约矩阵且有0≠αx≤Ax≤βx,αx≠Ax,Ax≠βx对某一非负向量x成立,则:α＜ρ(A)＜β,x是一正向量.

2 主要结论和证明

定理1 如果线性方程组(1)的系数矩阵A为非奇异的Z-阵,且满足

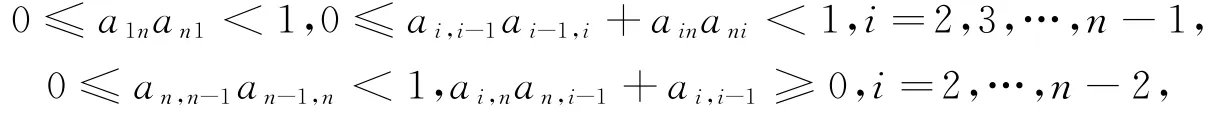
1)则 对于0＜ω≤1,当ρ(Lω)＜1时,有ρ(～Lω)＜1且ρ(～Lω)≤ρ(Lω)＜1.

2)若A是不可约的,且满足题设条件和0＜ω＜1,那么:

(1)若ρ(Lω)＜1,则ρ(～Lω)≤ρ(Lω)＜1;

(2)若ρ(Lω)＞1,则ρ(～Lω)≥ρ(Lω)＞1.

证 因为

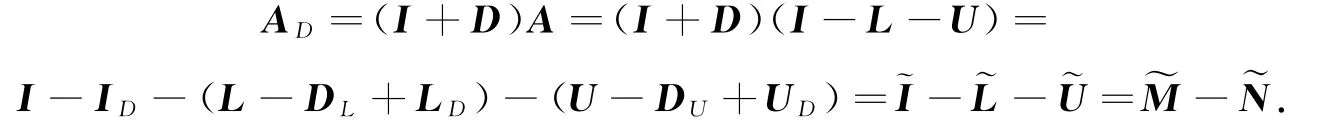
由条件

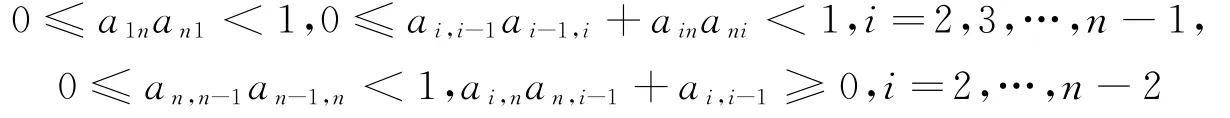
知,-DL+LD≥0且I-ID的主对角元素均大于零,所以

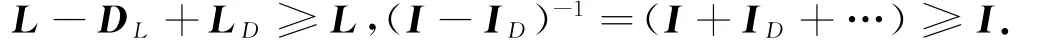
又

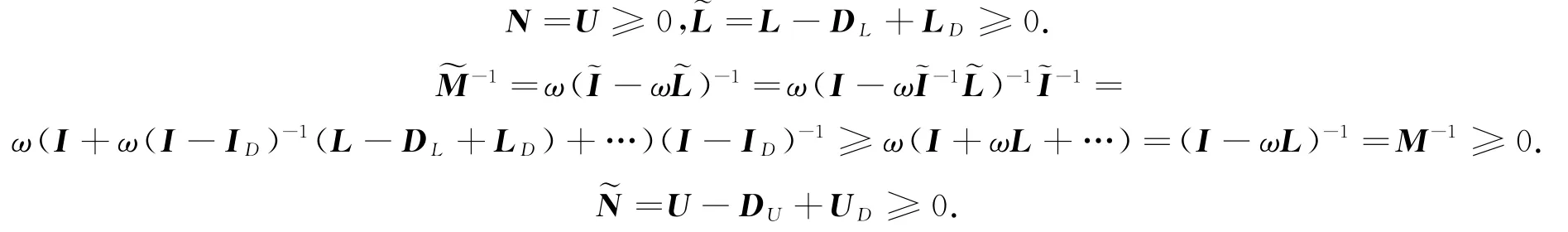
令

则

而

所以A=M-N=M1-N1均为A的弱正规分裂.又

所以M1-1≥M-1,N≥0.又ρ(M-1N)＜1,A-1≥0,ρ(M1-1N1)≤ρ(M-1N),所以ρ(～M-1～N)≤ρ(M-1N)＜1即ρ(～Lω)≤ρ(Lω)＜1.

下面证明2).因为A=I-L-U是不可约的,而

所以Lω也是不可约的.又Lω≥0,由引理2存在一向量x＞0与其相对应.设ρ(Lω)=λ,则有Lωx=λx,即

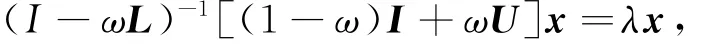
也即

因为

所以当λ-1＞0,即ρ(Lω)＞1时,～Lωx-λx≥0;(λ-1)＜0,即ρ(Lω)＜1时,～Lωx-λx≤0.由引理3可得定理结论(2)成立. ❙

3 数值例子

设线性方程组(1)的系数矩阵为

用ρ(GSS),ρ(GSR),ρ(GSD)分别表示在本文引言中提到的预条件P=I+S,P=I+R,及本文引言中提到的新的预条件P=I+D下SOR迭代矩阵的谱半径,它们的大小比较如下表1.

表1列出具体的计算结果,可以看出新的预条件比已有的预条件收敛速度更有优越性.

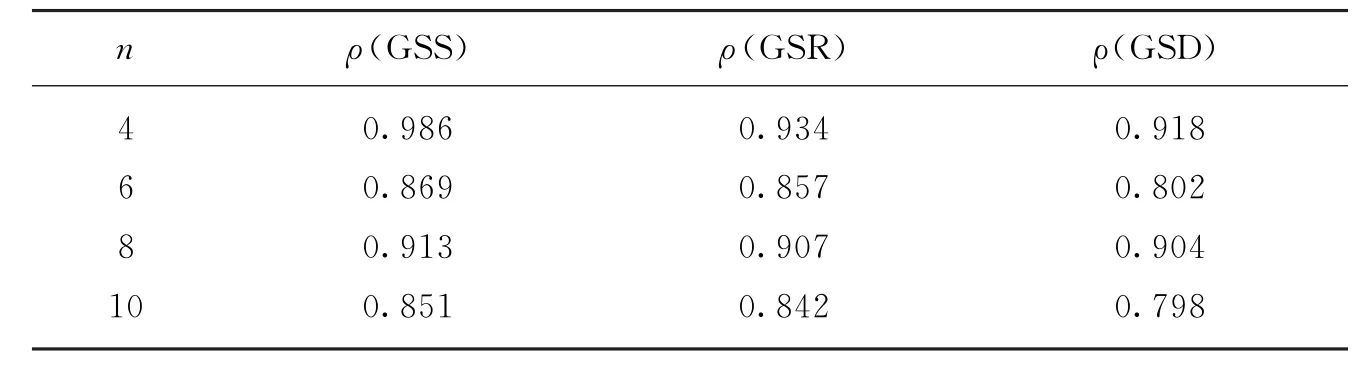
表1 ρ(GSS),ρ(GSR),ρ(GSD)的计算结果

参考文献:

[1]徐树方.矩阵计算的理论和方法[M].北京:北京大学出版社,1995:121-122.

[2]马如云,吴红萍.一类四阶两点边值问题多个正解的存在性[J].数学物理学报,2002,22A(2):244249.

[3]胡家赣.线性代数方程组的迭代解法[M].北京:科学出版社,1997:13-17.

[4]SUN J P,LIW T,ZHAO Y H.Three positive solutions of a nonlinear three-point boundary value problem[J].J Math A-nal Appl,2003,288:708-716.

[5]Berman A,plemmons R J.Nonnegative Matrices in the Mathematical sciences[M].London:Academic press,1979:25-32.