粗糙集预测算法的稳定性分析

张晓霞，陈德刚

(1.华北电力大学 控制与计算机工程学院，北京 102206；2.华北电力大学 数理学院，北京 102206)

0 引言

粗糙集理论[1]作为数据分析及知识发现的重要工具一直备受关注,如今粗糙集已广泛应用于机器学习[2]、数据挖掘[3]、决策分析[4]、专家系统[5]、智能控制等领域[6-7].由于决策信息系统中通常包含重复样本或不一致样本集(相同条件属性不同决策属性)，因此由其诱导的决策规则具有不确定性，自然地规则的测量以及算法的设计就成了粗糙集理论急需解决的问题之一.考虑到不一致决策信息系统的普遍性和重要性，文中主要考虑粗糙集预测算法的泛化能力.

目前，关于粗糙集的研究主要集中于构造预测算法的学习准则[8-10].Dai等[8]利用算法分类一致率提出了一个新的粗糙集算法；Skowron[9]基于一致矩阵和布尔逻辑提出了诱导规则方法；Yasdi[10]基于粗糙集模型设计了提取规则算法.这些算法都有一个共同目标：通过决策信息系统设计一个准则，然后根据这个准则预测新样本的标签.然而这些方法却没有数值刻画算法的预测能力，即度量学习准则的算法的性能-泛化误差.众所周知，算法的稳定性和泛化误差分析是机器学习和数据挖掘领域中最基本的问题，对该问题目前已有很多研究[11-16]，其中最突出的就是算法的扰动性分析[12]，用来测量训练集在微小变动情况下输出结果的变化.根据扰动性可以建立鲁棒性较好的系统，Bousquet等[13]基于扰动性分析定义了算法的稳定性，并且解释了如何根据经验误差和留一误差求得算法的泛化界.Wu等[14]利用留二法研究了学习算法的稳定性，并且定义了几种不同的留二法稳定性并研究了这些稳定性之间的关系.Rudin等[17]利用文献[13]的结果分析了最大置信度最小支持度及调节置信度算法的泛化界，这两种方法可以用来做序列事件预测及监督学习.基于这些考虑，本文利用算法稳定性研究粗糙集预测算法的泛化界.

文中设计了置信度算法，该算法可以预测新样本的标签，其原理就是寻找训练集中与新样本相同的等价类，然后分配与该等价类置信度最高的标签给新样本.首先定义了置信度函数，其次利用最小化算子定义了其损失函数，最后利用算法的稳定性给出了置信度算法的泛化界.结果表明，泛化界主要与决策信息系统中样本的数目及稳定性参数有关.对于大样本机制的决策信息系统，样本越多其诱导的决策规则越多，因此经验误差更逼近泛化误差，同时上界也更小.

1 预备知识

1.1 粗糙集

设S=(U,C,D={d})是一个决策信息系统，其中U={x1,x2,…,xn}为非空有限论域，C={c1,c2,…,cn}为非空有限条件属性集(特征)，D={d}是决策属性(标签).设Vc和Vd是特征c∈C和d的值域，记C(x)=(c1(x),c2(x),…,cn(x))∈Vc和D(x)∈VD分别为x关于特征C和决策属性D的值域.每个样本x可用条件属性和决策属性表示，即x:(C(x),D(x))∈Z=VC×VD，则决策信息系统可表示为

对任意的B⊆C，定义不可区分关系

则由INd(B)诱导的x的等价类为

[x]B={y∈U|c(x)=c(y),∀c∈B}.

对任意的X⊆U，定义X的B下近似集和B上近似集分别为

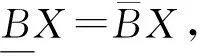
论域U关于IND(C)的划分为U/IND(C)={Φ1,Φ2,…,Φp}，其中Φj(j=1,2,…,p)是x关于IND(C)的等价类,U/IND(D)={Ψ1,Ψ2,…,Ψr}是U关于IND(D)的划分，Ψj(j=1,2,…,r)称为决策类.每个决策类的上下近似可以用来诱导决策规则.

决策规则[18-19]在粗糙集中可以表示为

C(x)→D(x)，

其中

C(x)和D(x)分别称为规则C(x)→D(x)的前件和结论.规则C(x)→D(x)的置信度定义为

其中#(·)表示集合所含元素的个数.若fS,0(C(x),D(x))=1，则决策规则C(x)→D(x)是确定性规则；否则是不确定的.

1.2 稳定性

如文献[5]所述，训练集通常表示为

其中xi∈X称为输入，yi∈Y称为xi的输出，X×Y独立同分布于未知分布D.

l(f,z)=c(f(x),y).

算法的泛化是定义在训练集S上的随机变量，即

由于分布D未知，所以借助经验误差Remp(A,S)和留一误差Rloo(A,S)来近似R(A,S)，即

其中Si={z1,z2,…,zi-1,zi+1,…,zm}.

给定带有m个样本的训练集S，PS[·]表示S关于Dm的概率，ES[·]为S关于Dm的期望.同样地，Px[·]和Es[·]分别为样本x关于D的概率和期望.

2 粗糙集预测的稳定性

粗糙集预测旨在从决策信息系统中学习规则从而对新样本预测标签.本节主要介绍如何基于粗糙集的置信度预测算法，并利用算法稳定性[5]刻画其泛化能力.

2.1 稳定性

给定决策信息系统S={x1=(C(x1),D(x1)),…,xm=(C(xm),D(xm))}.假设每条规则在S中至少出现2次，即样本中每个样本都存在与其具有相同条件和决策属性的其他样本.事实上该假设在大样本机制下是普遍的，当样本数m相对大时，每个样本都会重复出现多次，这也是粗糙集理论独特于其他理论之处.

粗糙集预测的主要任务是构造分类器，这里采用置信度测量规则C(x)→D(x)的可信度，则基于置信度的分类器构造如下：

(1)

gfS,0(x)主要用来寻找前件为C(x)且置信度最高的规则的后件，即

若|gfS,0(x)|>1，则满足最大置信度的标签不唯一，此时随机选一个作为x的标签，该算法称为基于粗糙集的置信度预测算法.

公式(1)表明：如果新样本x与训练集中某一样本y具有相同的特征值，则x的决策值是以C(y)为前件且置信度最大的规则的后件，并不一定与y的结论相同;若x与训练集中任一样本的特征值都不同，则置信度为0,任意的标签都可赋给x.

2.2 置信度预测算法的损失函数

为了讨论算法的稳定性，首先定义损失函数.给定一个带标签的样本x:=(C(x),D(x))，决策规则C(x)→D(x)的置信度fS,0的损失函数l(fS,0,C(x)→D(x))定义为

l(fS,0,C(x)→D(x))=min{1,1-Ω},

其中

称该损失函数为最小边界损失函数.

当间隔Ω≤0时，l(fS,0,C(x)→D(x))=1;若Ω>0时，损失值就是其间隔值的补偿值，即1-Ω.关于损失函数l的经验误差为

泛化误差是损失函数的期望，即

下面考虑用经验误差近似估计泛化误差，即尽可能地最小化

|TrueErr(fS,0)-EmpErr(fS,0)|，

该问题可以转化为:对任意的ε>0，最小化

PS[|TrueErr(fS,0)-EmpErr(fS,0)|>ε].

为方便讨论，首先引入以下记号：

·移除第i个对象，Si={x1,…,xi-1,xi+1,…,xn};

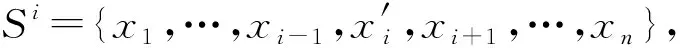
由于假设每条规则至少在训练集中出现2次，所以当移除或替换某个样本后，规则数目不会减少，但置信度会变化，因此留一法的边界损失为

粗糙预测算法的稳定性基于多维随机函数的一阶差分建立，下面定理1对随机变量的方差[20]给出了上界，定理2是指数界[21].

则

粗糙预测算法的稳定性基于多维随机函数的一阶差分建立.

2.3 置信度预测算法的稳定性及泛化界

类似于文献[13]中定理17，下面讨论置信度算法的稳定性.算法稳定性的概念最早提出于20世纪70年代，主要用来测量算法在训练集有微小变动(移除或删除一个元素)时算法的泛化能力.类似于文献[13]中定义15，下面给出置信度算法强稳定性的概念.

定义1置信度算法关于边界损失函数l具有强稳定性β，如果对任意的有

其中∞范数对所有规则适用.

定义1可以诱导得到置信度算法的一致稳定性.根据文献[13]，置信度的点对假设稳定性定义如下：

定义2置信度算法关于边界损失函数l具有点对假设稳定性β，如果对任意的k∈{1,2,…,m}有

当改变某个样本时，训练集中可能会新增一条规则，因此点对假设稳定性考虑了平均边界损失.

引理1若置信度算法关于边界损失函数l具有强稳定性β，则其具有一致稳定性.

证明

其中

其中第一个不等式利用绝对值的三角不等式，第二个不等式利用强稳定性的定义. 】

下面利用点对假设稳定性给出了置信度算法的泛化界，其证明类似于文献[13]的定理11.

定理3设S是一个含有m(m≥2)个元素的决策信息系统，置信度算法关于边界损失函数l具有点对假设稳定性β，则对任意的δ∈(0,1)，以下结果至少以概率1-β成立：

定理3表明置信度算法的泛化界由样本数m和稳定性参数β控制：样本数越多，参数β越小，泛化界越小.事实上当样本数增多时，算法的学习能力也会增强，同时样本数增多会给新样本提供更多参考，因此增加样本数从而提高算法泛化能力的估计是很容易理解的.同样地，当稳定性参数β减小时，改变训练集中的某个样本，边界损失的平均值改变很小，充分说明改变样本对算法的影响不大，反应了算法良好的稳定性.因此β越小，对算法的泛化界的估计越精确.

下面计算定理3中点对假设稳定性的β的具体值.首先引入下列符号：

#k([z]C)表示等价类[z]C的样本个数，其中z∈Sk,[z]C表示删除第k个样本之后论域Sk生成的等价类，即[z]C∈Sk;

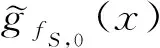
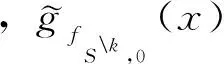
因此

表示除规则C(x)→D(x)之外，在S上生成的所有决策规则C(x)→D(y)的最高置信度与Sk上生成的所有决策规则C(x)→D(y)的最高置信度的差.

定理4设S是一个含有m(m≥2)个元素的决策信息系统，由S生成的规则集为

则对任意规则C(x)→D(x)∈AS,有

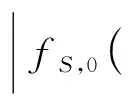
(2)|fS,0(C(x),D(x))-

fSk,0(C(x),D(x))|≤

证明(1)C(x)表示x的特征值，#(C(x))表示与x具有相同特征的样本数目，因此

删除第k个样本，则xk要么属于[x]C要么不属于,所以

首先计算

的上界.根据置信度算法，样本x在Sk诱导的规则C(x)→gfSk,0(x)的置信度超过C(x)→gfS,0(x)的置信度，即

因此

同理，x在S上诱导的规则C(x)→gfS,0(x)的置信度超过C(x)→gSk,0(x)的置信度，即

从而

因此

(2)当xk从S中删除后,

i)若xk∈[x]C∩[x]D，则

因此

由于假设每条规则至少出现2次，因此

易得

从而

ii)若xk∈[x]C∧Ck∉[x]C∩[x]D，则

因此

iii)若xk∉[x]C，则

fS,0(C(x),D(x))-fSk,0(C(x),D(x))=0.

从而

定理4给出了置信度算法强稳定性的β值，定理4(2)刻画了同一条规则在删除样本前后置信度的变化.结果表明置信度算法的强稳定性参数与等价类的大小有关，等价类越粗，稳定性参数越小.

推论1根据引理1和定理3，对任意的C(x)→D(x)∈AS，有

证明利用定理4和三角不等式易得. 】

推论1刻画了置信度算法的一致稳定性，且其稳定性参数与等价类大小有关.

引理2设S是一个含有m(m≥2)个元素的决策信息系统，对任意的等价类[x]C∈S/C，有

其中pC(x)是样本x取特征值C(x)的概率.

由于等价类[x]C服从二项分布，即#([x]C)～B(m,pC(x))，引理2的证明可参考文献[22].

定理5设S是一个含有m(m≥2)个元素的决策信息系统，置信度算法满足点对假设稳定性β，由系统生成的规则集为

则对任意的γ>0及δ>0，不等式

TrueErr(fS,0)≤EmpErr(fS,0)+β1,

至少以概率1-δ成立,其中

证明由于推论1对所有规则都通用，根据引理2，对规则C(xk)→D(xk)，有

对任意的xk∈S,pmin≤pC(xk)，根据引理2，对任意的1≤k≤m有

因此

应用上述参数β于定理4中可得定理5. 】

定理5刻画了点对假设稳定性下置信度算法的泛化界.结果表明置信度算法的泛化界由数据的粒度及样本数决定，大样本机制下粒化越粗，置信度算法的经验误差越接近其泛化误差.

3 结束语

粗糙集预测是粗糙集理论中不确定性学习的关键问题，其下近似诱导确定性规则而上近似诱导不确定规则.通常确定性规则的前件具有唯一的结论，而不确定性规则的结论不唯一，这也是粗糙集理论与其他学习理论的不同之处，即粗糙集理论可以处理这种不确定和不一致决策信息系统.文中采用置信度算法度量这种不确定规则，并且利用稳定性理论刻画了置信度算法的泛化能力.结果表明置信度算法的泛化能力与决策信息系统的样本数目及稳定性参数有关，样本越多，稳定性参数越小，则泛化能力越强.

下一步将讨论基于其他类型粗糙集的预测算法的泛化能力.

:

[1] PAWLAK Z.Rough sets[J].InternationalJournalofComputerandInformationSciences,1982,11(5):341.

[2] ZHANG J B,WONG J S,PAN Y.et al.A comparison of parallel large-scale knowledge acquisition using rough set theory on different map reduce runtime systems[J].InternationalJournalofApproximateReasoning,2014,55(3):896.

[3] CHEN H,LI T,LUO C,et al.A decision-theoretic rough set approach for dynamic data mining[J].IEEETransactionsonFuzzySystems,2015,23(6):1958.

[4] HUANG C H.Medical reasoning with rough-set influence diagrams[J].JournalofComputationalBiologyAJournalofComputationalMolecularCellBiology,2015,22(8):752.

[5] HUANG M J,ZHANG Y B,LUO J H,et al.Evaluation of economics journals based on reduction algorithm of rough set and grey correlation[J].JournalofManagement&Sustainability,2015,5(1):140.

[6] BAI C,SARKIS J.Green supplier development:analytical evaluation using rough set theory[J].JournalofCleanerProduction,2010,18(12):1200.

[7] TAN Z,LIWEI J U,CHEN Z,et al.An environmental economic dispatch optimization model based on rough set theory and chaotic local search strategy differential evolution algorithm[J].PowerSystemTechnology,2014,38(5):1339.

[8] DAI J H,TIAN H W,WANG W T,et al.Decision rule mining using classification consistency rate[J].Knowledge-BasedSystems,2013,43:95.

[9] SKOWRON A.Extracting laws from decision tables:a rough set approach[J].ComputationalIntelligence,1995,11(2):371.

[10] YASDI R..Learning classification rules from database in the context of knowledge acquisition and representation[J].IEEETransactionsonKnowledgeandDataEngineering,1991,3(3):292.

[11] ALON N,BEN D S,CESA B N,et al.Scale-sensitive dimensions,uniform convergence,and learnability[J].JournaloftheACM,1997,44(4):615.

[12] BONNANS J F,SHAPIRO A.Optimization problems with perturbation,a guided tour[J].SIAMReview,1998,40(2):228.

[13] BOUSQUET O,ELISSEEFF A.Stability and generalization[J].JournalofMachineLearningResearch,2002,2:499.

[14] WU J,YU X,ZHU L,et al.Leave-two-out stability of ontology learning algorithm[J].ChaosSolitons&Fractals,2016,89:322.

[15] DEVROYE L,WAGNER T.Distribution-free performance bounds for potential function rules[J].IEEETransactionsonInformationTheory,1979,25(5):601.

[16] VAPNIK V N.EstimationofDependencesBasedonEmpiricalData[M].New York:Springer,1982:186.

[17] RRDIN C,LETHAM B,MADIGAN D.A learning theory framework for sequential event prediction and association rules[J].JournalofMachineLearningResearch,2013,14:3441.

[18] KRYSZKIEWICZ M.Comparative study of alternative types of knowledge reduction in inconsistent systems[J].InternationalJournalofIntelligentSystems,2001,16(1):105.

[19] KRYSZKIEWICZ M.Rules in incomplete information systems[J].InformationSciences,1999,113:271.

[20] STEELE J M.An Efron-Stein inequality for nonsymmetric statistics[J].AnnalsofStatistics,1986,14(2):753.

[21] MCDIARMID C.OntheMethodofBoundedDifferences[M].Surveys in Combinatorics.Cambridge:Cambridge University Press,1989:148.

[22] GRZEGORZ A R.Asymptotic factorial powers expansions for binomial and negative binomial reciprocals[J].ProceedingsoftheAmericanMathematicalSociety,2004,132(1):261.