基于BP神经网络的傅里叶核函数拟合研究
任东红 ,林 鹏 ,袁清萍 ,邢兵锁 ,董国贵
(1.铜陵职业技术学院,安徽 铜陵 244000;2.国网铜陵供电公司,安徽 铜陵 244000)
一、引言
随着人工智能科学的发展,人工神经网络也迅速成为预测领域较常用的智能建模方法,尤其是针对工程中高度非线性的复杂系统,难以用普通的数学方法准确建模,人工神经网络其本身的特点能够学习和分析大量的输入-输出数据,而无需给定输入-输出之间的函数映射关系,因此其可以广泛应用于高阶非线性系统建模,解决复杂系统的黑箱模型问题[1-3]。BP神经网络是经典的人工神经网络模型之一,其运用误差反向传播算法(BP算法)建立多层的前馈神经网络模型,通过对给定大数据的学习,确定各层神经元连接权值,最终建立神经网络模型,拟合复杂系统,从而应用于工程实践。文中针对傅里叶核函数法拟合精度较低的问题,运用BP神经网络进行建模,函数曲线拟合精度较高。
二、建立BP神经网络
BP神经网络是常见的多层前馈神经网络,由输入层、隐含层、输出层组成,图1所示为一个三层的BP神经网络,即输入层、隐含层、输出层分别只有一层,其中x1,x2,…xn为神经网络的n维输入,y1,y2,…ym为神经网络的m维输出,wij表示神经网络输入层第i个神经元到隐含层第j个神经元的连接权值,wjk表示隐含层第j个神经元到输出层第k个神经元的连接权值。若要准确的拟合函数,必须确定隐含层神经元个数以及各神经元之间的连接权值,从而建立精确地神经网络模型。文中将采用试探法确定隐含层神经元个数,通过误差反向传播算法(BP算法)确定各神经元之间的连接权值。其中神经网络的输入层和输出层神经元的作用函数为线性函数,即神经元的输出值等于其输入值;隐含层神经元的作用函数选择常用的Sigmoid函数;隐含层和输出层神经元的输入值分别等于上一层神经元输出值的加权和[4]。
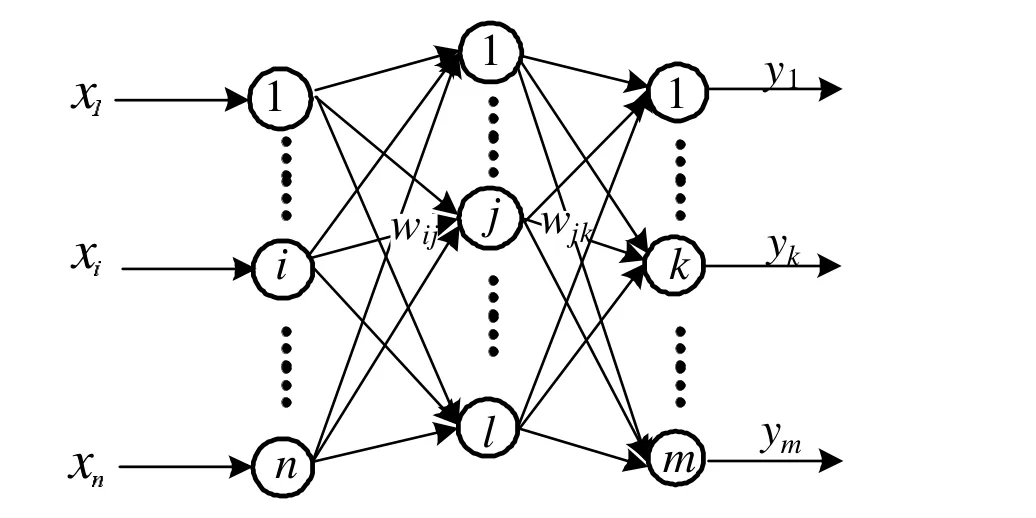
图1 三层BP神经网络
三、BP学习算法
BP学习算法即误差反向传播算法,是一种有导师的学习算法。它的学习过程由两个部分组成:正向传播过程和反向传播过程。正向传播是指将学习的样本数据输入到神经网络的输入层,输入层神经元接受到传播信号,依据神经元的作用函数再将信息传到隐含层(1层或多层),隐含层依据神经元作用函数再将信息输出传入至输出层神经元的输入,最终根据输出层神经元的作用函数计算输出层的输出。反向传播是指将神经网络的实际输出值与期望输出值比较,如果误差不满足设定的要求,将误差向回传播,同时根据误差调整各神经元的连接权值,直至误差满足要求。

图2 BP算法信息传播流程图
图2 是BP学习算法的信息传播流程图,具体过程描述如下:
信息的正向传播:
BP神经网络输入层第i个神经元的输出为:

公式(1)中ui表示输入层第i个神经元的输入值。
隐含层中第j个神经元的输入xjH为:

公式(2)中,wijH表示输入层第i个神经元到隐含层第j个神经元的连接权值。
隐含层中第j个神经元的输出yjH为:

公式(3)中表示隐含层第 j个神经元的作用函数,文中选用Sigmoid函数。
输出层第k个神经元的输入为

公式(4)中,wjkO表示隐含层第j个神经元到输出层第k个神经元的网络连接权值。
输出层第k个神经元的输出ykO为
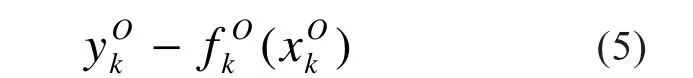
其中表示输出层第k个神经元的作用函数,文中选用线性函数。
信息的反向传播:信息的反向传播目的是调整连接权值,降低误差。设神经网络的实际输出值为y,神经网络的期望输出值为t,则它们之间的误差为e(e=t-y),误差从输出层反向传播,同时在传播过程中通过求导的方式对神经网络中各神经元之间的连接权值不断修正,使神经网络的实际输出值y与期望输出值t之间的误差减小,直至误差达到给定值以下,网络训练结束[5][6]。
神经网络神经元连接权值训练的流程图如下:
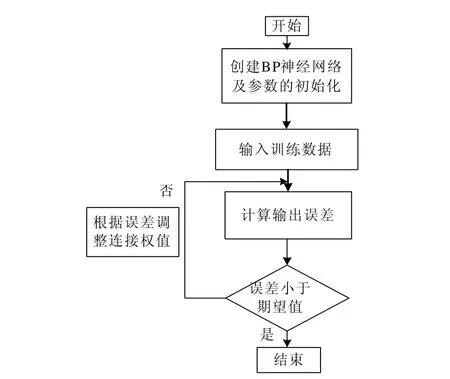
图3 BP神经网络的训练流程图
四、神经网络模型训练及预测结果
本实验的目的是对傅里叶核函数f(x)=sinx/x进行拟合,首先是建立精确的BP神经网络拟合模型。由于文中只是针对一维多个历史数据进行训练,不考虑其他因素对神经网络的影响,因此输入层神经元个数选择1即可,输出层神经元个数也选择1。现在最重要的是确定隐含层神经元个数,本文通过试探法确定。分别选定神经网络的隐含层神经元个数为5,10,20三个数,通过训练结果及测试结果的比较,最终选定合适的隐含层神经元个数。训练及测试结果如下。当隐含层神经元为5时,得到的训练结果如下:
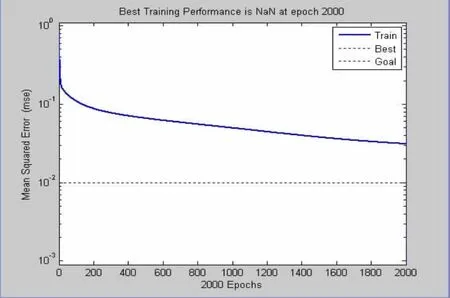
图4 训练步数与训练误差关系图
当隐含层神经元为10时,得到的训练结果如下:
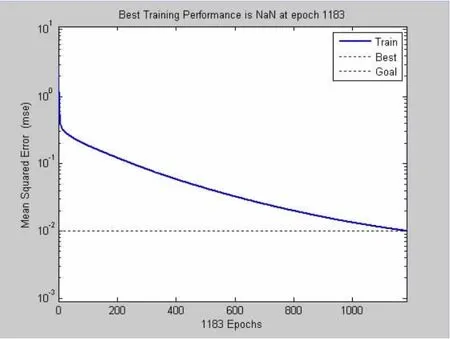
图5 训练步数与训练误差关系图
当隐含层神经元为20时,得到的训练结果如下:

图6 训练步数与训练误差关系图
图4 ,5,6中,蓝色实线表示训练误差与训练步数之间的关系曲线,黑色虚线表示停止误差为0.01。从图4中可以看出,当隐含层神经元数目为5时,训练步数达到最大训练步数2000步时仍然大于给定的允许误差0.01;图5中可以看出,当隐含层神经元数目为10时,训练效果明显优于第一种,当训练步数为1183步时,即可达到误差0.01;图6中可以看出,当隐含层神经元数目为20时,训练效果更优,当训练步数为870时即可达到给定的误差范围之内。
为了得到最优的神经网络,不仅需比较训练效果,同时要考虑测试效果,即模型的精确性。建立的3个模型的测试效果如下。
当隐含层神经元为5时,测试结果如下:
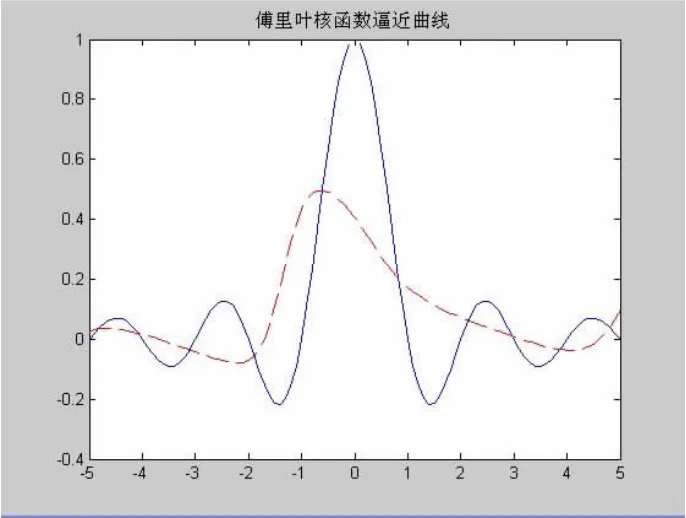
图7 函数拟合曲线(神经元数5)
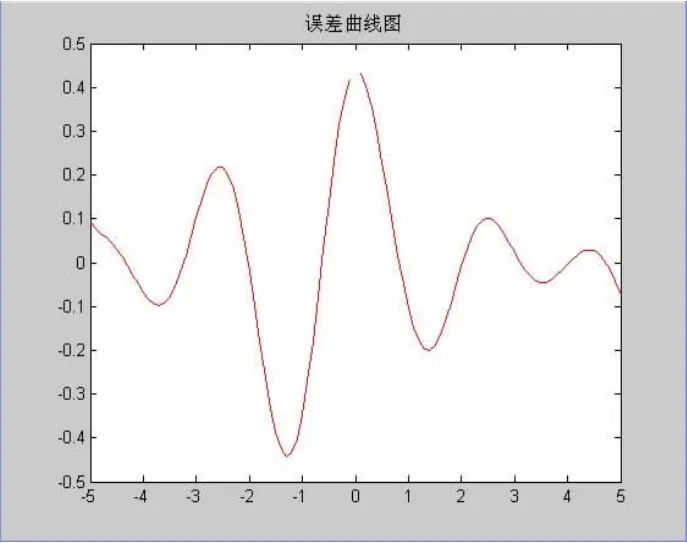
图8 误差曲线图(神经元数5)
当隐含层神经元个数为10时,函数拟合曲线及误差曲线如图下:
图9 函数拟合曲线(神经元数10)

图10 误差曲线图(神经元数10)
(3)当隐含层神经元数目为20时,测试结果如下:
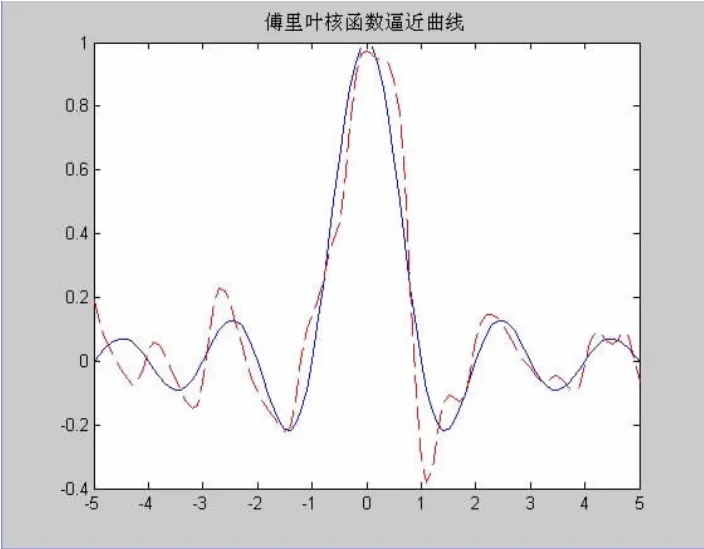
图11 函数拟合曲线(神经元数20)

图12 误差曲线图(神经元数20)
当隐含层神经元数分别为5,10,20时测试结果如下表:

表1 神经网络测试结果比较
图7,9,11为神经网络函数拟合曲线图,其中蓝色实线为模型的期望输出,红色虚线表示模型的实际输出。从图形7,9,11可以直观地看出隐含层神经元个数为10时,函数拟合情况明显优于其他两种模型。图8,10,12为神经网络模型拟合的误差曲线图,表1表示神经网络输出值与实际输出值得比较值,从误差曲线图以及表1中可以看出隐含层神经元个数为10时平均误差为10.03%,优势明显。
五、结论
建立准确的非线性函数模型在工程中具有重要意义,文中通过应用前馈神经网络模型以及BP学习算法建立三层的BP神经网络模型用于傅里叶核函数拟合实验。同时通过试探法确定神经网络隐含层神经元个数,从实验结果可以得出,神经网络隐含层神经元个数并不是越多越好,当隐含层神经元个数过多时会导致训练复杂,函数可能会偏离实际输出。因此通过实验比较确定本神经网络模型隐含层神经元个数为10时,预测效果最佳,此时建立的模型可以较好地应用在非线性函数拟合中。
[1]郝海霞.用粒子群算法优化BP神经网络进行函数拟合[J].山西师范大学学报,2017,31(1):14-16.
[2]徐富强,钱云,刘相国.GA-BP神经网络的非线性函数拟合[J].微计算机信息,2012,28(7):148-150.
[3]乔冰琴,常晓明.改进粒子群算法在BP神经网络拟合非线性函数方面的应用[J].太原理工大学学报,2012,43(5):558-563.
[4]刘俊.BP神经网络在多维非线性函数拟合中的应用[J].商洛学院学报,2014,28(6):19-22.
[5]任东红.基于集成神经网络的污水处理出水水质软测量模[D].北京:北京工业大学,2010:27-28.
[6]RUMELHART D E,HINTON G E,WILLIAM SR J.Learning Internal Representations by Error Propagation[C].Parallel Distributed Proceeding.Cambridge,1986:318-362.

