课堂意外是培养学生数学核心素养的绝佳时机——以一堂函数图像的探究课为例

☉浙江省宁波市北仑中学 毛浙东

自从高中课标修订组提炼出六个数学学科核心素养“数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析”以来，我们广大的一线教师积极响应，在课堂教学设计中，融入了很多核心素养的元素，这是令人欣喜的.

记得章建跃先生曾说：“数学课改的核心任务是提升学生的数学学科核心素养，要把数学学科核心素养的培育落实在数学教育的各个环节.”王尚志教授也指出：“培养并提升核心素养，需要理解、感悟，需要主动、自觉地将‘学生为本’的理念与教学实际有机结合.”

既然要将核心素养的培育落实到教育的各个环节，那我们不能只把目光集中在课堂预设中；既然我们要主动、自觉，将“学生为本”的理念与教学实际有机结合，我们就应该更多地关注课堂中的意外生成.

其实，课堂意外正是培养学生核心素养的绝佳时机.下面，笔者就以自己执教的一堂函数图像的探究课为例，来与各位同行一起探讨一下，如何在课堂意外中捕捉培养学生核心素养的机会，希望能抛砖引玉.

一、课堂实录

（一）踏破铁鞋无觅处——课堂意外，喜得方法

师：我们今天来探究形如的函数的图像和性质.下面我们先来研究特殊情形：即研究函数的图像与性质.

当笔者利用描点法画出了图1，并想继续往下讲解时，忽然听到学生1的笑声.

图1

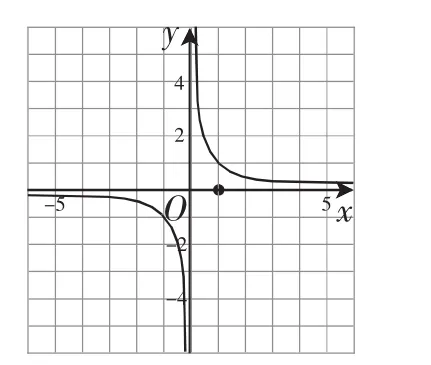
图2

笔者估计生1可能发现了什么，便示意他起身回答.

生1：这不是被挤扁了的反比例函

师：你挺有想象力嘛，不过今天我们研究的这个函数叫做“对勾函数”，和反比例函数还是有所区别的.

生1：没什么区别啊，就是被挤压后的反比例函数嘛.

笔者一听来了兴致，便继续追问.

师：那你说说看，它是怎样被挤压的呢？

生1：函数在平面直角坐标系xOy中的图像如图2所示.如果将x轴逆时针旋转45°，即将平面直角坐标系xOy挤压变形得到新的坐标系x′Oy.那么在新坐标系中，函数的图像其实就是原坐标系xOy中的函数y=.也就是说，要得到函数的图像，只需先画出函数y的图像，然后把x轴逆时针旋转45°，跟着被挤压变形的函数的图像就是的图像.

（二）莫畏浮云遮望眼——适时引导，摸索规律

师：这位同学旋转坐标轴的方法倒是蛮有创意，刚刚他将x轴逆时针旋转了45°，那如果我们将x轴顺时针旋转45°，又会得到什么结论呢？

在教师的启发下，学生展开了探究，不一会就有学生举手.

生2：我按照生1的方法，先作出函数的图像，将x轴按顺时针旋转45°，得到新坐标系x′Oy，则在新坐标系中原函数的图像被拉伸成了新函数，其图像如图3所示，它恰好就是函数的图像.

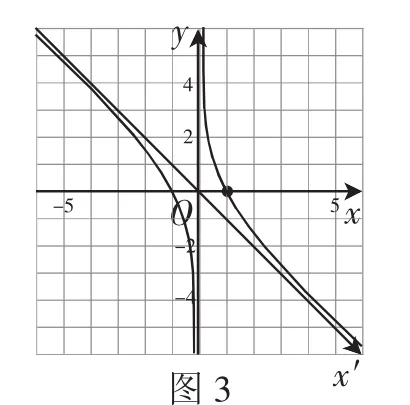
图3

师：很好，对于原函数，若将x轴按照逆时针旋转45°，就能得到的图像，将x轴按照顺时针旋转45°，就能得到的图像.那我们如果将原函数改变一下，比如改成，那刚才的旋转作图是否还有效呢？

生3：如果将x轴逆时针旋转45°，被拉伸后的函数y=的图像就是原坐标系xOy中的函数的图像，如图4所示；如果将x轴顺时针旋转45°，跟着被挤压后的函数的图像就是原坐标系xOy中的函数的图像，如图5所示.

图4

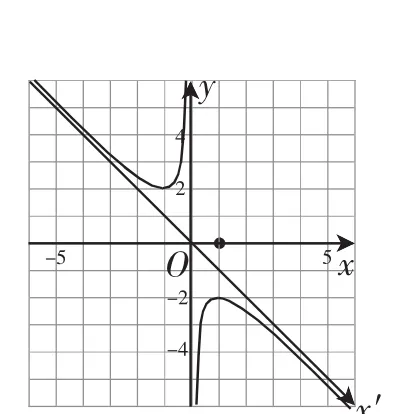
图5

师：很好，看来改变原函数的解析式，这种旋转的规律依然适用，现在不妨换一个角度，我们每次是否只能旋转45°，比如旋转30°行不行呢？大家不妨探究一下.

生4：对原函数将x轴逆时针旋转30°，被挤压后的函数的图像就是在原坐标系xOy中的函数y=的图像，如图6所示.同理，将x轴顺时针旋转30°，被拉伸后的函数图像就是在原坐标系xOy中的的图像，如图7所示.

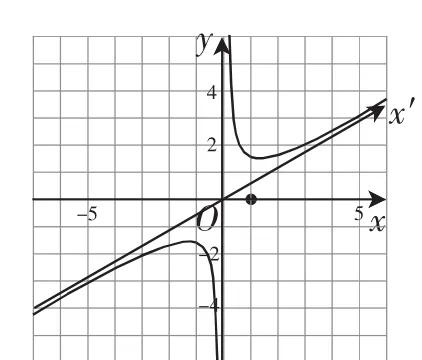
图6

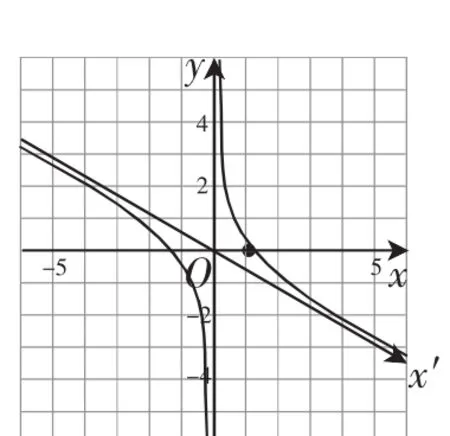
图7

师：你能够验证刚才的猜想吗？

生4：利用计算机画出函数与函数y=的图像，我们发现恰好是函的图像的渐近线，这可以说明将x轴逆时针旋转30°，函数就被挤压成

师：不错，那大家是否能据此归纳出更一般性的结论呢？

经过交流讨论，学生得出了如下的定理.

定理：在平面直角坐标系xOy中，保持y轴不动，将x轴按逆时针旋转α（0°＜α＜90°），则跟着被挤压（或拉伸）后的函数k≠0）的图像就是原坐标系xOy中的函+tanα·x（k≠0，0°＜α＜90°）的图像；将x轴顺时针旋转α，则挤压（或拉伸）后的函数的图像就是原坐标系xOy中的函数-tanα·x（k≠0，0°＜α＜90°）的图像.

（三）宜将剩勇追穷寇——继续探究，扩大战果

经过进一步探究，学生发现，这不仅只是对反比例函数挤压（或拉伸）才有效，对任意的幂函数y=xn，如果将x轴进行旋转，都有类似的结论成立.

推论1：在平面直角坐标系xOy中，保持y轴不动，将x轴逆时针旋转α（0°＜α＜90°），则跟着被挤压（或拉伸）后的函数y=kxn（k∈R，n∈R）的图像就是原坐标系xOy中的函数y=kxn+tanα·x（k∈R，n∈R，0°＜α＜90°）的图像；将x轴顺时针旋转α（0°＜α＜90°），则挤压（或拉伸）后的函数y=kxn（k∈R，n∈R）的图像就是原坐标系xOy中的函数y=kxn-tanα·x（k∈R，n∈R，0°＜α＜90°）的图像.

比如，在平面直角坐标系xOy中，将x轴逆时针旋转45°，则函数y=x2的图像也跟着变形，得到了函数y=x2+x的图像，如图8所示.

其实，对任意的函数f（x），也有这样的结论，见推论2.

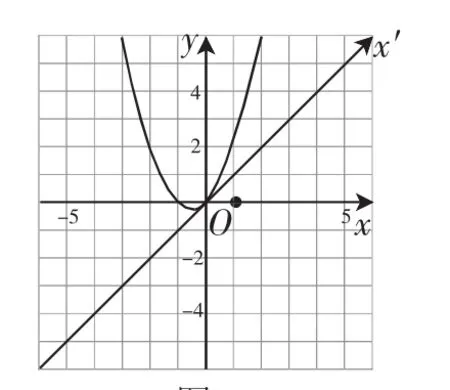
图8

图9

推论2：在平面直角坐标系xOy中，保持y轴不动，将x轴逆时针旋转α（0°＜α＜90°），则跟着被挤压（或拉伸）后的函数y=f（x）的图像就是原坐标系xOy中的函数y=f（x）+tanα·x（0°＜α＜90°）的图像；将x轴顺时针旋转α（0°＜α＜90°），则挤压（或拉伸）后的函数y=f（x）的图像就是原坐标系xOy中的函数y=f（x）-tanα·x（0°＜α＜90°）的图像.

比如，在平面直角坐标系xOy中，画出函数y=sin x的图像，现将x轴逆时针旋转45°，则原函数y=sin x的图像也跟着变形，得到了函数y=sin x+x的图像，如图9所示.

（四）吹尽狂沙始到金——深入思考，发现本质

师：保持y轴不动，对x轴旋转角度α（0°＜α＜90°），其实质是将原坐标平面内的每一个点（x，y）进行了怎样的变换呢？

生：其实就是把点（x，y）变成了点（x，y+tanα·x）.

师：同学们，那我们能否据此给坐标轴的旋转下一个定义呢？

经过提炼与修正，学生最终得出了如下的定义.

坐标轴旋转：在平面直角坐标系中，保持y轴不动，对x轴旋转角度α（-90°＜α＜90°），等价于将坐标平面内的任意一个点P（x，y）对应成新的点P′（x，y+tanα·x）.

根据此定义，我们就不难理解刚才得到的定理与推论了.

此时课堂已近尾声，但学生的探究热情未减，于是笔者干脆让同学们在课后继续分组研究，下面是其中一个小组极具创意的成果.

（五）喜看稻菽千重浪——课后研究，再结硕果

A小组的研究成果：

我们把情况从二维跨越到三维，想象现在眼前有一个空间直角坐标系，其中O为原点，x轴，y轴，z轴两两垂直，那么空间中的每一个点都能被准确定位.在日常生活中，这已满足我们的需要.但在不同的环境下，一些超强的引力兴许会扭曲这个时空，地球也不例外.

比如，在地球中，物体都会受到地球的万有引力的影响.

如图10，这是一座钟塔，一开始，两个钟被调到相同的时间.但过了几十年、几百年，会发现上面的时间与下面所显示的相差了几秒.钟当然没有问题，问题出在两个钟所在的时空受地球引力的影响而发生了扭曲，从而导致经过的时间存在了差异.

若在某三维空间附近存在一强引力（比如，较大的恒星或黑洞），那么此三维空间便不再正常，即时空会出现扭曲.现以O为原点建立空间直角坐标系，则空间的扭曲可看作是将某个（或某几个）坐标轴进行了旋转，于是我们可以用到之前得出的结论，即变化量分别为tanα·x或tanα·y或tanα·z.此时，若要求在强引力附近某物体的运动轨迹，我们就可以用坐标轴旋转的定义来解决.

图10

举个例子，假设某物体初始时是呈直线运动的，为了简单起见，我们假设其运动轨迹为直线y=x，在经过强引力附近时，若x轴发生了扭曲，设扭曲角为α（-90°＜α＜90°），则我们就可以计算出物体的实际运动轨迹为y=x+tanα·x.

二、教学感悟

本堂课笔者本希望能与学生共同研究函数y=（ab≠0）的图像与性质，却止步于画图环节，真可谓是意外.但失之东隅却收之桑榆，本课虽然没有完成预设的教学任务，却更好地培养了学生的数学核心素养，而且站在整个高中教学的视野下看，这样的课堂意外，少了刻意的雕琢，多了灵气的原生态，反而对学生的学习品质的养成更为有利.

（一）顺水推舟，培育学生的直观想象能力

直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的过程.它主要包括：借助空间认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系等.

在本课中，教师原本预设了用描点作图的方法来得到函的图像，但学生却意外地提出了旋转法，此处的课堂生成是非常有价值的.我们知道，描点法虽然可以做到精细化作图，但缺少了图像动态变化的过程，失去了培育学生直观想象力的大好机会.空间想象可分为静态图形的想象和动态图形的想象，其中动态图形的想象更为复杂，对思维要求更高，学生舍弃了相对“静态”的描点法，采用了更为“动态”的旋转法，不失为一种上乘的选择.同时，教师在课堂中顺水推舟，营造民主的学习氛围，让学生放开手脚大胆探索，让学生的想象力得以自由释放，从而探究出林林总总旋转后的图形，极大地培育了学生的直观想象能力.

（二）适时引导，提升学生的数学抽象能力

数学抽象是指舍去事物的一切物理属性，得到数学研究对象的思维过程.它主要包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并且用数学符号或者数学术语予以表征.

在本课中，教师不断改变函数的解析式，并适时引导学生从一个个具体的函数中抽象出最本质的属性，最终发现了图形的旋转与函数解析式之间的内在关联，从而得到了一般性的结论.这个过程就是数学抽象的过程，在这个抽象过程中，既有对图形的抽象提炼，也有对代数解析式的抽象提炼，更有图形和代数解析式之间关联性的抽象提炼，可谓是把抽象思维的培育做到了淋漓尽致.

比如，从旋转45°，到旋转30°，再到旋转α，这些是对图形特征进行抽象提炼；而从具体的反比例函数到一般的反比例函数再到函数y=kxn，最后推广到函数y=（f x），则是对代数解析式的抽象提炼；至于将x轴逆时针旋转45°，对应着函数解析式值增加了x，从而抽象出将x轴逆时针旋转α，对应着函数解析式增加了tanα·x，则是对图形和代数解析式之间关联性的抽象提炼，而坐标轴旋转定义的形成更是将这种形与数之间关联性的提炼推向了高潮.

（三）搭建平台，发展学生的数学建模能力

数学建模是指对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程.它主要包括：在实际情境中从数学的视角发现问题、提出问题、分析问题、构建模型、求解结论、验证结果并改进模型，最终解决实际问题.

由于课堂时间有限，教师鼓励学生在课后继续进行分组探究，教师搭建了平台，学生则登台唱戏.每个研究小组都获得了各自的研究成果，以A小组的研究成果为例，学生从实际问题出发，将课堂中二维坐标系的旋转升级为了三维空间坐标系的旋转，并给出了扭曲的时空中运动物体的定位方法，虽然观点略显稚嫩和粗糙，但难能可贵的是，学生已经学会了运用数学的眼光来看待实际问题，用数学的方法来分析实际问题，用数学的模型来刻画实际问题.学生的数学建模能力在合作研究中得以发展，学生的数学视野也在交流碰撞中得以开阔.

1.水菊芳.基于数学核心素养的课堂数学意识的构建［J］.数学通报，2016（11）.

2.任伟芳.为培育核心素养，凸显概念教学过程而设计［J］.中学数学教学参考，2016（11）.

3.毛浙东.把握动态生成，构建和谐课堂［J］.中学数学教学参考，2008（9）.

4.毛浙东.数学概念课我们如何上得精彩［J］.中学数学，2010（6）.F