求解椭圆球面波函数以及改进措施研究

郝海玲

(晋中职业技术学院 车辆工程系，山西 晋中 030600)

PSWF椭圆球面波函数是一种以频域能量聚集性、近似时限带限、时域双正交、频谱可控等性能为开发方向的计算模型。Pollak与Slepian等早在1962年便提出了椭圆球面波函数的集合算法构思，并在此后的几十年中相继发表了众多研究成果[1]。本研究在众多研究成果之上借鉴了PSWF椭圆球面波函数的采样定理模型，优化配置了运算模型的可行性求解方案。现做如下分析。

1 研究背景

1.1 PSWF椭圆球面波函数的应用优势

目前，PSWF椭圆球面波函数被广泛应用于小波信号的分析作业中，并发挥出比sinc函数更为突出的时间分辨率。而且在应用此函数之后，可以将数字与图像信号进行优化处理，进而解决空间与时间分辨率低的相关问题。同时在无线通讯的相关研究中表明，PSWF椭圆球面波函数能够优化高速移动通信效果，进而规避视频选择性较低的问题。通过加强信号设计便可以有效控制频谱，并达到提升频谱功率的最佳效果[2]。尤其在利用了PSWF椭圆球面波函数的高能量聚集性以及正交性之后，可以有效调节非正弦时域的正交调制，较OFDM调制效果更佳，能够将高频带利用率提升至2 Baud/Hz以上，具备了提升功率利用率，同时相对系统结构较为简单的优势。

1.2 求解椭圆球面波函数的关键问题

目前PSWF椭圆球面波函数的求解精准度始终是关注度最高的研究焦点，而且也并无极为精准的解析表达方式，严重限制了其广泛应用的推广条件。PSWF椭圆球面波函数目前仅能提供近似求解方法，主要分为两中求解路径，分别为数值求解算法，以及重构求解算法。

一方面，Legendre多项式求解算法，是PSWF函数中最为经典的重构算法之一，能够改进PSWF微分方程，并通过迭代运算以及矩阵特征值进行重构求解[2]。但是利用此类算法必须经过矩阵和过迭运算的复杂流程，虽然相对提升了求解精度，但是在运算量较大时，其运算效率相对过低，无法作为优化PSWF椭圆球面波函数求解算法的主要方式。

另一方面，Halpern等针对椭圆球面波函数积分方程的定义进行了数值求解方法的优化，利用PSWF椭圆球面波函数的纯数值进行求解。数值求解方法将积分方程的特征函数解析问题转化为Toeplitz矩阵的特征向量求解，运用矩阵向量解析PSWF椭圆球面波函数的离散采样值。具备求解便捷性较高的特征，并不需要采集大量基础数据能够有效提升运输效率，因此被广泛应用于UWB脉冲波形的优化设计方案中[3]。但是数值求解方法只能解析PSWF椭圆球面波函数的离散采样值，并不具备广泛应用的求解价值。此后，Kedar等提出了基于PSWF椭圆球面波函数特征的重构解析思路，在求解离散采样值的基础上，依据采样定理进行近似值的求解。但是仍然仅能完成近似值的解析，而且需要构建大量矩阵模型，相对的运算量较大，且运算效率较低。

2 PSWF椭圆球面波函数的重构求解运算模型

通过采样定理可知，在任意带的有限信号中，带通信号与基带信号均属于不产生混叠效果的信号频谱类型，一旦采样信号出现了失真现象并无法快速划分其原始信号。而PSWF椭圆球面波函数作为时限带限函数的特殊类型，具备了较强的运算效果[4]。通过PSWF椭圆球面波函数ψ(t)所具备的近似带限特征，可以满足离散采样的重构需求。首先需要设定ψ(t)的中心频谱为f0，并设定带宽为B。在对于的等间隔T中，其运算模型为：

公式一：

在此公式中采样信号的频谱可以设定为运算模型：

公式二：

而该公式中的信号采样频率为：f=1/T

依据次采样定理可以明确ψ(t)的最低频率必须控制在(f0～B/2)之间，且必须为带宽B的整数倍，因此中心频率与相应带宽必须满足f0=(Q+1/2)B的等价关系成立[5]。而其中Q≧1以及无限接近于Z时，则代表采样频率的最小取值空间可以保证2B的已知条件。并在不发生混叠信号频率的情况下进行运算。如果将Ψ(ω)的频谱取值空间设定在{f0-B/2}到{f0+B/2}的范畴之列，则可以利用带通频率的滤波器进行频谱采样，其理论模型为：

公式三：

而在进一步运算中可以明确时间卷积定理的运算条件，并通过以下运算流程求得：

公式四：

在此公式中g(t)代表了带通滤波其的时域冲击响应条件，如果最低频率出现了大于带宽B的非整数条件，则会出现B’≧B的情况，此时f0=(Q+1/2)B’的条件较为充分。假设取值采样频率为2B’时，采样信号不发生混叠现象，且能够保持一定的频谱间隙。则可以将{f0-B’/2}到{f0+B’/2}的取值空间作为滤波其的无失真恢复信号源，其运算模型为：

公式五：

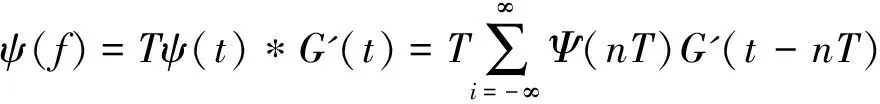
对比公式四与公式五可知，在其重构函数中虽然存在一定差异，但是基于采样定理的考量维度，信号波的选择空间与椭圆球面波函数的求解本质相同，也可以作为PSWF椭圆球面波函数的求解通式。

3 椭圆球面波函数的改进措施

PSWF椭圆球面波函数作为时限带限函数的特殊类型，具备了较强的运算效果，但是并无法直接快速求解相似值。而依据采样定理将sinc基函数的相关时域性融入椭圆球面波函数之中，能够重构基函数G(t)的精准度，并优化PSWF椭圆球面波函数的重构求解效率。因此，可以根据采样定理分析PSWF椭圆球面波函数的运算机理，并设计相应的运算流程。以G(t)函数模型从时域到频域的构建次序，可以首先考量函数的基本运行条件，并圣地函数的取值空间，在频率处于全新的正交基函数模型中并获得相应频谱条件后便可以推导出G(f)的时域冲击相应函数，其运算模型为：

公式六：

而在B=2kHz的情况下，满足sin(t)=sinπt/πt的已知条件，因此在sin(2Bt)的波形图中能够发现基函数的具体特征，并在其函数时域中体现为加强的收敛性能。而求解基函数的过程中，可以在[-B，B]的椭圆球面波函数重构条件下完成，因此相应的收敛特征可以支持运算精度。同时也可以在获取信号x0(t)中表示为载波低通信号x(t)的运算模型，通过等价条件约束f0的带通中心频率，其运算模型为：

公式七：x0(f)=1/2[x(f-f0)+x(f+f0)]

因此即便在统一的频谱取值空间[-B0/2,B0/2]内，相应的基带信号x(t)在经过转化之后，也会产生完全不同的频谱形状，而频谱取值范围也可以定义为：[f0-B0/2,f0+B0/2]。那么PSWF椭圆球面波函数在实际运算过程中，由于提高了根本的收敛性能，因此也可以快速求得近似值，其运算效率与运算精度均可有效提升。

4 结语

虽然依次罗列了重构基函数的具体步骤，但是在实际运算中，必须充分考察其收敛速度与收敛频次，否则也无法优化椭圆球面波函数的求解效果。反之，在公式六与公式七的运算条件下，椭圆球面波函数运算模型的具体细则相对清晰，且具备了快速收敛特征，因此可以作为提高椭圆球面波函数运算精准度的必要措施。而且PSWF椭圆球面波函数本身的重构求解流程中，可以适当引入仿真模型作为考察结果，可以通过理论分析与仿真分析获取PSWF函数在实际应用过程中的求解便捷性。那么PSWF椭圆球面波函数在实际运算过程中，由于提高了根本的收敛性能，因此也可以快速求得近似值，其运算效率与运算精度均可有效提升。因此，可以在获取基函数时域收敛性能的基础上提升其运算精准度，完善那么PSWF椭圆球面波函数的求解过程。

[参考文献]

[1]刘晓,王红星,刘传辉,张磊.椭圆球面波函数时频能量聚集性研究[J].中国电子科学研究院学报,2015,10(03):237-244.

[2]康家方,王红星,刘传辉,赵志勇,刘锡国.基于IDFT的椭圆球面波函数重构产生方法[J].上海交通大学学报,2014,48(03):357-362.

[3]钟佩琳,王红星,赵志勇,陈昭男.椭圆球面波函数微分系统求解及仿真[J].吉林大学学报(工学版),2013,43(06):1675-1679.

[4]潘耀宗,孙小东,钟佩琳,刘传辉,王红星.一种新的基于椭圆球面波函数的非正弦短波通信的均衡方案[J].电子与信息学报,2012,34(12):2862-2868.

[5]钟佩琳,王红星,赵志勇,刘锡国,刘传辉.基于状态转移矩阵逼近的椭圆球面波函数求解方法[J].电子与信息学报,2012,34(10):2427-2431.