离散时间代数Riccati矩阵方程对称解的双迭代算法
刘 敏
(忻州师范学院 五寨分院,山西 忻州 034000)
1 引言
Riccati矩阵方程及其解法的应用很广,尤其是在线性二次优化和振动控制等领域有广泛应用。
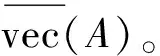
时间离散代数Riccati矩阵方程DTARME(Discrete Time Algebraic Riccati Matrix Equation)可以表示为式1-1:
ATXA-X-(ATXB+L)(R+BTXB)-1(BTXA+LT)+G=O
(1-1)
上式中,A,G∈Rn×n,R∈Rm×n,B,L∈Rn×m,并且rank(B)=m,R和G-L-LR-1LT是对称的正定矩阵。方程1-1在最优控制系统以及状态评估领域发挥着非常重要的作用,例如最大成本估算、最优调节器设计以及过滤器设计等方面的实用价值非常强大。为了书写和表达的简便,取LT=O,R=I,获得DTARME的标准表达形式,即式1-2:
ATXA-X-ATXB(I+BTXB)-1BTXA+G=O
(1-2)
2 DTARME标准方程对称解的牛顿算法
为了方便本文的计算和书写,引入ψ(X)和φX(Y),其中:
ψ(X)=ATXA-X-ATXB(I+BTXB)-1BTXA+G
(1-3)
φX(Y)=ATYA-Y-ATYB(I+BTXB)-1BTXA
-ATXB(I+BTXB)-1BTYA+ATXB(I
+BTXB)-1BTYB(I+BTXB)-1BTXA
(1-4)
假设上式中BTYB(I+BTXB)-1的谱半径小于1,那么可以推导出:
ψ(X+Y)=ψ(X)+φX(Y)+γ(Y),其中γ(Y)可以表示为式(1-5):
γ(Y)= -ATYB(I+BTXB)-1BTYA+ATXB(I
+BTXB)-1BTYB(I+BTXB)-1BTYA-
(BTYB(I+BTXB)-1)K)BT(X|+Y)A
+ATYB(I+BTXB)-1BTYB(I
+BTXB)-1BT(X+Y)A
(1-5)
此处,φX(Y)是指ψ(X)中的点x沿着Y的方向求得的Frechet倒数。
引理1 假设X∈Ω是DTARME方程(1-2)的近似解,那么方程的对称解可以表示为X*=X+Y,即等价与求证值Y∈Ω满足ψ(X+Y)=O,根据可线性化方式求的Y∈Ω,满足φX(Y)=-ψ(X)。
证明:假设有X∈Ω为方程(1-2)的近似解,设X*=X+Y,则求解X*∈Ω的过程相当于求证Y∈Ω满足ψ(X+Y)=O,即未知矩阵Y相关的非线性矩阵方程。根据牛顿算法的原理,如果Y范数比较小,那么Ψ(X+Y)=Ψ(X)+φX(Y)+γ(Y)中的非线性部分γ(Y)可以舍去,则Ψ(X+Y)=Ψ(X)+φX(Y)+γ(Y)的近似表达式为:
Ψ(X+Y)≈Ψ(X)+φX(Y)
(1-6)
因此,求解对称解X*∈Ω的过程可以近似转化为求解φX(Y)+Ψ(X)=O的过程,所以,需要求得满足φX(Y)=-Ψ(X)的Y∈Ω,证毕。
在引理1中,一般来说,φX(Y)=-Ψ(X)的解并不是方程Ψ(X+Y)=O的精确解,所以X*∈Ω也并不是方程Ψ(X)=O的精确解,但是可以将这个解看作是近似解。修改矩阵的类型,得到求解方程(1-2)对称解的牛顿算法,求解过程可以表示为以下三个步骤:
第一步:确定初始矩阵X(1)∈Ω,设k:=1;
第二步:假设Ψ(X(k))=O,求解结束;否则,求解Y(K)∈Ω,确保:
φX(k)(Y(k))=-Ψ(X(k))
(1-7)
第三步:计算X(k+1)=X(k)+Y(k),设k:=k+1,则继续执行第二步。
需要特别指出的是,在牛顿算法中,如果线性矩阵方程没有满足条件的对称解Y(k),那么可以用对称的Ls解来替代,这也是双迭代算法的一个关键特征。
3 求解线性矩阵方程对称解与对称Ls解的MCG算法
首先建立求解线性矩阵方程对称解和对称Ls解的MCG算法,线性矩阵方程的一般形式可以表示为:
(1-8)
上式中,Ai,Y,BiF∈Rm×n。
待求解问题1:当线性矩阵方程(1-8)有对称解,那么求解满足方程(1-8)的Y∈Ω。
待求解问题2:当线性矩阵方程(1-8)无对称解,那么求解Y∈Ω,使:
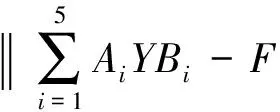
(1-9)
3.1 问题1的MCG求解算法
记
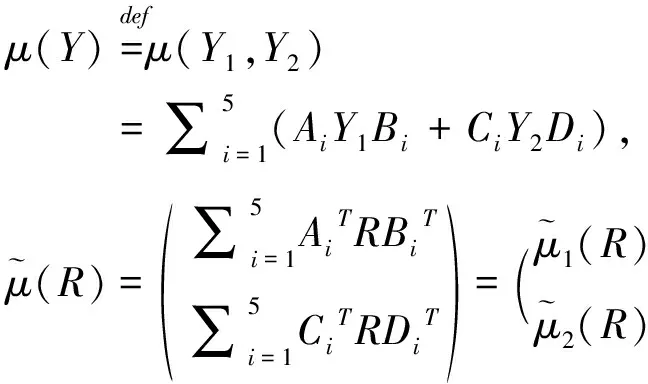
第一步:给定两个初始化矩阵,分别表示为Y1(1),Y(2)∈SRn×n,设置k:=1,计算
Rk=F-μ(Y(k))
(1-10)
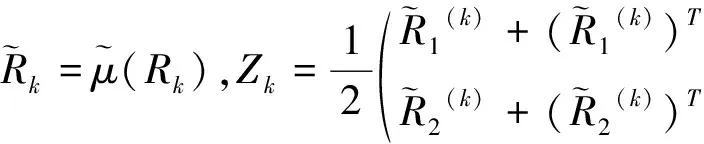
(1-11)
第二步:如果Rk=O或者Rk≠O,Zk=O那么计算结束;
否则计算:

k:=k+1时,继续进行第二步。
计算结果表明算法1中的矩阵满足下列收敛定理:
定理1:假设问题1相容,那么对于任意的初始化矩阵Y1(1),Y2(2)∈SRn×n来说,算法1都可以在有限的计算中获得线性矩阵方程(1-8)的对称解。
定理2:假设问题1相容,选择初始矩阵Y1(1),Y2(2),使其满足下列条件:

(1-12)
那么算法2可以在有限计算之后获得问题1的唯一且极小范数解。
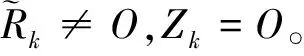
3.2 求解问题2的MCG算法
记:

(1-13)
定理4:问题2的求解等价与求f(Y)=Q的对称解,并且一定存在对称解。
证明:求解问题2等价与存在Y1,Y2∈SRn×n满足
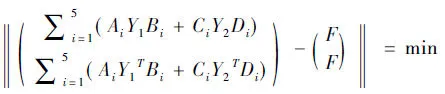
(1-14)
等于求解矩阵方程组
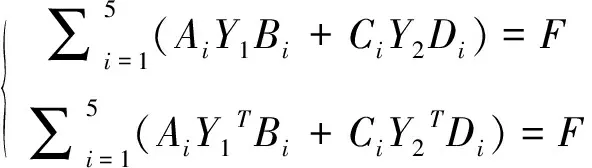
可以表示为线性代数方程组:

(1-15)

求解问题2的MCG算法可以表示为:
第一步:给定两个初始化矩阵,分别表示为Y1(1),Y2(2)∈SRn×n,设置k:=1,计算


第四步:k:=k+1时,继续进行第二步。
由此可以得出,算法2中的矩阵满足Y1k,Y2k,P1(k),P2(k)∈SRn×n,对于算法2有和算法1类似的收敛性定理。
4 总结
采用牛顿算法求解DTARME(1-2)方程的对称解,利用MCG算法求解每一步迭代计算导出方程的对称解,建立求解矩阵方程的对称解双迭代计算方法,结果表明这种双迭代算法有效。若修改初始矩阵的类型,那么这种双迭代算法可以应用于其他DTARME(1-2)方程特殊解的求解中。
[参考文献]
[1]李书连,张凯院,刘晓敏. 一类矩阵方程异类约束解与Ls解的迭代算法.高校应用数学学报[J].2012,27(3):313-324.
[2]廖福成,刘贺平.带有状态时滞的多采样率线性离散时间系统的最优预见控制器设计[J].北京科技大学学报,2008,30(40:452-460.
[3]朱寿升,张凯院.一类双变量Riccati矩阵方程组对称解的迭代算法[J].工程数学学报,2014(1):93-102.
[4]王成,朱经浩.一类随机Riccati矩阵代数方程的线性迭代解法[J]. 山东理工大学学报(自然科学版)》,2006,20(1):32-35.
[5]李学俊.离散时间代数Riccati方程的解法研究[D]. 西安:西北工业大学,1999.

