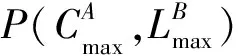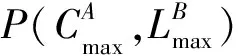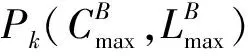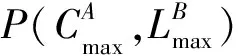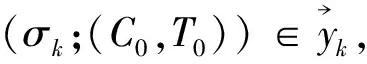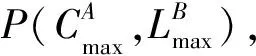具有一致性的双代理有界序列分批排序问题
何 程,韩鑫鑫
(河南工业大学 理学院,河南 郑州 450001)
1 引言
多代理排序问题是Baker和Smith[2]最先引入的。 有几个代理,每个代理有一个工件集和一个目标函数。这些代理的工件必须在一个共同的加工资源(例如,一台机器)上被加工,并且每个代理都希望最小化各自的目标函数,每个代理的目标函数只与他自己工件的完工时间相关。我们的问题是找到一个满足每个代理的目标函数要求的排序。
多代理排序问题起源于需要多方协商解决问题的情形。它在工业管理、电信服务等方面应用广泛 (见[4]和[9])。 现在多代理排序问题已被广泛研究。Agnetis等人[1]研究了单机多代理排序问题,他们考虑的目标函数是正则函数(单调非减函数)的最大值,误工工件数和加权总完工时间。Cheng等人[3]和原晋江[10]也研究了单机上的多代理排序问题。Leung等[8]研究了两个代理的一致平行机排序问题。
本文考虑序列分批模型,该模型中,工件被分批加工,并且同一批工件具有相同的开工时间和完工时间,每批工件的加工时间等于该批中所有工件的加工时间和,且加工每一批工件前,机器都有一个安装时间。对于同时最小化A代理的时间表长和B代理的最大延迟的无界序列分批排序问题,冯琪等[5]给出了一个多项式时间算法来找到该问题的所有Pareto最优解。对于Pareto最优排序问题1|s-batch,b (3.1) (3.2) 因此我们有下列引理。 由上述算法,我们可以通过下面的算法POP找到所有的Pareto最优点。 算法POP [参考文献] [1]A. Agnetis, D. Pacciarelli, A.Pacifici, Multi-agent single machine scheduling[J]. Ann. Oper. Res.,2007,(150) :3-15. [2]K.R. Baker, J.C. Smith, A multiple-criterion model for machine scheduling[M]. Journal of Scheduling, 2003,(6) :7-16. [3]T.C.E. Cheng, C.T. Ng, J.J. Yuan. Multi-agent scheduling on a single machine with max-form criteria[J]. Eur. J. Oper. Res., 2008,(188):603-609. [4]I. Curiel, G. Pederzoli, S. Tijs, Sequencing games[J]. Eur.J. Oper. Res., 1989, (40)344-351. [5]Q. Feng, Z.Y. Yu, W.P. Shang, Pareto optimization of serial-batching scheduling problems on two agents[C]. ICAMechS, ISBN 978-1-4577-1698-0. [6]R.L. Graham, E.L. Lawler, J.K. Lenstra, A.H.G. Rinnooy Kan, Optimization and approximation in deterministic sequencing and scheduling: A survey[J]. Annals of Discrete Mathematics, 1979, (5):287-326. [7]C. He, H. Lin, Y.X. Lin, Bounded serial-batching scheduling for minimizing maximum lateness and makespan[J]. Discr. Opti., 2015,(16): 70-75. [8]J. Y. -T. Leung, M. Pinedo, G. Wan, Competitive two-agent scheduling and its applications[J]. Oper. Res. 2010,(58):458-469. [9]D. Schultz, S. H. Oh, C. F. Grecas, M. Albani, J. Sanchez,C. Arbib, V. Arvia, M. Servilio, F. Del Sorbo, A. Giralda, G.Lombardi, A QoS concept for packet oriented SUMTS services[M]. In: Proceedings of the 1st Mobile Summit, Thessaloniki, Greec (2002). [10]J.J. Yuan, Complexities of some problems on multi-agent scheduling on a single machine[J].J. Oper. Res. Soc. China, 2016,(4):379-384.2 预备知识
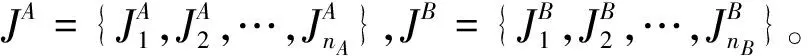







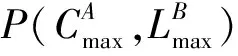
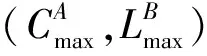
3 Pareto最优算法