一类有限区间上Kuramoto Sivashinsky方程的初边值问题
王宏伟,贺怡婷,杨彩凤,宗 慧
(安阳师范学院 数学与统计学院 河南 安阳455000)
1 引言
Kuramoto[1]在研究三维反应扩散系统的角相位湍流时,导出了如下一类四阶非线性方程
ut+uxxxx+uxx+uux=0
(1)
同时, Sivashinsky[2]在研究二维空间微热扩散不稳定性问题时也导出了相同的数学模型. 因此, 方程(1)被称为KS方程. 该方程Cauchy问题的研究, 已有很多结论[3,4]. 本文将在有限区间[0,L]上研究如下一类线性KS方程的初边值问题
{ut+uxxxx+uxx=f,0≤x≤L,t≥0
u(0)=φ(x),
u(0,t)=g0(t),ux(0,t)=g1(t),
u(L,t)=h0(t),u(L,t)=h1(t)
(2)
根据近年来由Fokas[5-7]创立的UTM方法, 我们给出这个方程的一个显式解公式, 该公式将为这类方程适定性问题和数值计算的研究提供新的研究思路.
2 显式解的推导过程
利用Fourier变换易知, 方程(1)的象征是ω(k)=k4-k2.假设e-ikx+ω(k)tu是方程(2)的一个解, 则
(e-ikx+ω(k)tu)t=e-ikx+ω(k)tf-[e-ikx+ω(k)t(uxxx+ikuxx-(k2-1)ux-(ik3-ik)u)]x.
在区域D={0≤x≤L,0 ∬D(e-ikx+ω(k)tu)tdtdx- ∬D[e-ikx+ω(k)tfdtdx =-∬D[e-ikx+ω(k)t(uxx+ikuxx-(k2-1)ux-(ik3 -ik)u)]xdtdx. 使用格林公式, 有 -(ik3-ik)u)dt 即 -1)ux(0,s)-(ik3-ik)u(0,s))dt -1)ux(L,s)-(ik3-ik)u(0,s))dt 定义空间变量在区间[0,L]上的函数u(x,t)的Fourier变换为 另外, 记 则下列等式成立 =-m3(ω(k),T)-ikm2(ω(k),T)+(k2-1)m1(ω(k),T)+(ik3-ik)m0(ω(k),T) +eikL[n3(ω(k),T)+ikn2(ω(k),T)-(k2-1)n1(ω(k),T)-(ik3-ik)n0(ω(k),T)] 将上式中的T替换为t, 并令 M(k,t)=m3(ω,t)+ikm2(ω,t)-(k2-1)m1(ω,t)-(ik3-ik)m0(ω,t), (3) N(k,t)=n3(ω,t)+ikn2(ω,t)-(k2-1)n1(ω,t)-(ik3-ik)n0(ω,t). (4) 则有 (5) 根据方程(2)的初始条件和边界条件, 在(5)式中, 只有m3,m2,n3,n2是未知项, 其他各项均可以用已知条件来表示. 下面我们来计算m3,m2,n3,n2. 解方程λ4-λ2=k4-k2,有四个根, 分别是 将λj(j=1,2,3,4)依次替换(5)中的k, 令 得到方程组 {m3+iλ1m2-e-iλ1L[n3+iλ1n2]=μ1, m3+iλ2m2-e-iλ2L[n3+iλ2n2]=μ2, m3+iλ3m2-e-iλ3L[n3+iλ3n2]=μ3, m3+iλ4m2-e-iλ4L[n3+iλ4n2]=μ4. 解这个方程组, 得到 其中 在复平面上定义区域G={k|Re(ω(k))<0}, 如果k=x+yi,则区域G可以表示为 {(x,y)|x4-6x2y2+y4-x2+y2<0}. (6) 由复变函数中的Cauchy定理知, (7) (8) 就可以得到本文的主要结论. 定理1 初边值解问题(1)的显式解是 [参考文献] [1]KURAMOTO Y, TSUZUKI T. On the formation of dissipative structures in reaction-diffusion systems[J]. Theor. Phys, 1975, 54: 687-699. [2]SIVASHINSKY G I. Nonlinear analysis of hydrodynamic instability in laminar flames-I Derivation of basic equations[J]. Acta Astronaut, 1977, 4: 1177-1206. [3]TADMOR E. The well-posedness of the Kuramoto Sivashinsky equation[J]. SIAM J. Math. Anal, 1986, 17:884-893. [4]COLLET P, ECKMANN J P, EPSTEIN H, STUBBE J. A global attracting set for the Kuramoto Sivashinsky equation[J]. Comm. Math. Phys, 1993, 152: 203-214. [5]FOKAS A S. A unified transform method for solving linear and certain nonlinear PDEs[J]. Proc. Roy. Soc. London Ser. A, 1997, 453: 1411-1443. [6]HIMONAS A A, MANTZAVINOS D. The “good”Boussinesq equation on the half-line[J]. J. Differential Equations, 2015, 258(9): 3107-3160. [7]FOKAS A S. HIMONAS A A, MANTZAVINOS D, The Korteweg de Vries equation on the half-line[J]. Nonlinearity, 2016, 29(2): 489-527.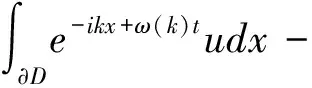
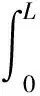






3 结论



