基于Julia分形的多涡卷忆阻混沌系统∗

肖利全 段书凯 王丽丹

1)(西南大学电子信息工程学院,重庆 400715)

2)(非线性电路与智能信息处理重庆市重点实验室,重庆 400715)

1 引 言

1971年,Chua首次提出忆阻器[1];2008年,惠普实验室率先研发出忆阻器实物模型[2].自此,忆阻器在非易失存储[3]、联想记忆[4]、非线性电路与系统[5]等众多领域有了广泛的应用.

分形[6−8]与混沌是紧密联系的,虽然分形与混沌的起源不同,发展过程也不相同,但它们的研究内容在本质上有着很大的相似性,混沌主要在于研究过程的行为特性,分形更着重于研究吸引子自身的结构.混沌吸引子也是分形集,而分形集便是动力学系统中那些不稳定轨迹的初始点的集合.对混沌和分形这两个领域的研究已硕果累累[9−14],Bouallegue[15]通过复杂的分形网络及变换产生混沌吸引子,作为联系如此紧密的两个学科,将分形与混沌系统相结合的研究是有意义的.

基于此,本文探索分形与混沌系统的结合,将经典的Julia分形过程及其变形应用于忆阻混沌系统中,数值仿真结果表明,它能产生多涡卷混沌吸引子,而且它的涡卷数可通过参数很好地进行控制.在已有的产生多涡卷混沌吸引子的方法中,如分段线性函数[16]、阶跃函数[17]、正弦函数[18]、开关流形[19−21]、时滞饱和序列[22−25],这些使用功能函数产生多涡卷混沌吸引子的方法,使混沌系统变得不光滑,而将分形过程应用于混沌系统产生多涡卷混沌吸引子的方法,则弥补了这一不足.

本文第2部分构建了一个新的忆阻混沌系统,并对它的动力学特性进行了分析,验证了系统的混沌特性;第3部分将Julia分形过程、带系数的Julia分形过程、高阶Julia分形过程和多项式Julia分形过程分别应用到本文提出的忆阻混沌系统中,得到了复杂多变的混沌吸引子,如环形多涡卷混沌吸引子,还讨论了分形过程中一个复常数的影响,通过改变复常数的取值,能够得到多种形状的混沌吸引子,如趋于分离状的多涡卷混沌吸引子;第4部分是本文的总结.

2 新忆阻混沌系统及其动力学性质

2.1 新忆阻混沌系统的提出

本文构建了一个新的忆阻混沌系统,可由以下方程描述:

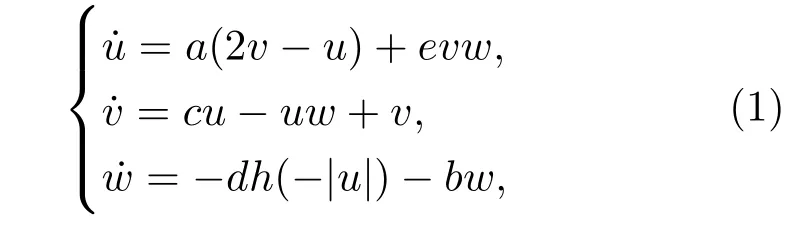
其中,a,b,c,d,e为系统参数;u,v,w为状态变量.h(·)满足二氧化钛忆阻器的磁通与电荷之间的关系,可表示为[12]

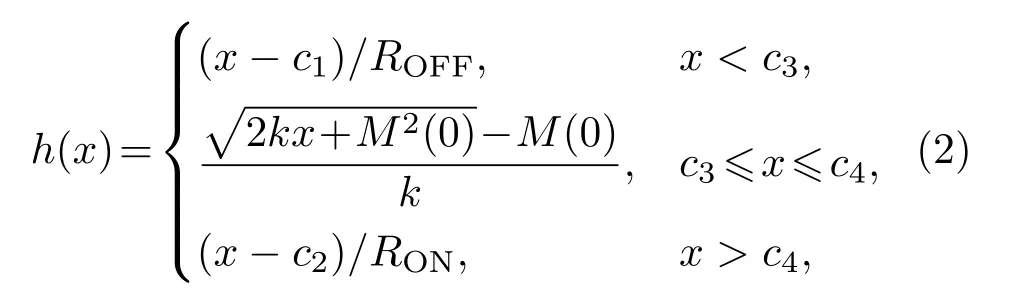
2.2 动力学特性

2.2.1 对称性和不变性

观察系统方程(1)不难发现,在坐标变换(u,v,w)→(−u,−v,w)下,系统(1)的微分方程保持不变.也就是系统(1)关于w轴对称.

2.2.2 耗散性

将系统(1)改写成下面的矢量形式:

向量场F(X)在R3上的散度为

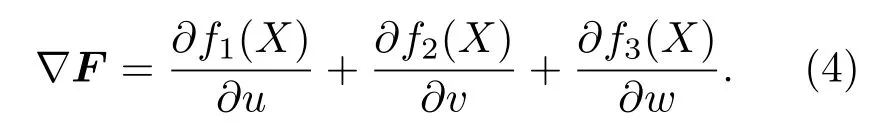
图1 系统(1)的混沌吸引子 (a)三维图;(b)u-v平面;(c)u-w平面;(d)v-w平面Fig.1.Attractor of system(1):(a)Three-dimensional view;(b)u-v plane;(c)u-w plane;(d)v-w plane.

对于系统(1),它的散度可以计算为∇F=1−a−b.当1−a−b<0时,∇F0.体积(V)的收缩速率为

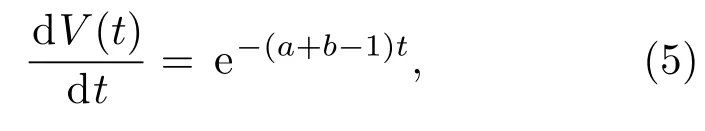
求解可得

系统的体积元以指数形式快速缩减到0.本文所选取的参数a=8,b=5,则∇F=1−a−b=−12<0,故系统(1)是耗散的.当t→∞时,每个体积元组成的系统轨道以指数(1−a−b)缩小到0.因此,系统的所有轨迹被限制在一个包含零体积的有限集内,且收敛到一个零体积的吸引子上.

2.2.3 系统平衡点

为了得到系统(1)的平衡点,令方程(1)中的可得

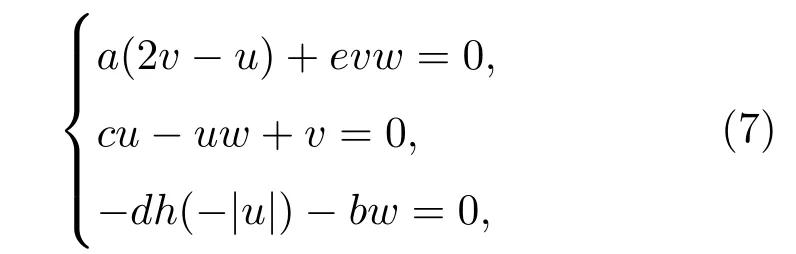
求得系统(1)在参数a=8,b=5,c=3,d=100000,e=12时,有三个平衡点S1(0,0,0),S2(3.9129,0.4053,5.1036)和S3(−3.9129,−0.4053,5.1036).

系统(1)线性化的Jacobian矩阵为

将平衡点S1代入(8)式,得到系统(1)在平衡点S1处的特征值λ1=−13.5125,λ2=6.5152,λ3=−3.λ1和λ3为负实根,λ2为正实根,故平衡点S1是不稳定的鞍点.

在平衡点S2(3.9129,0.4053,5.1036)处,求得其特征值为λ1=−10.4769+10.1340i,λ2=−10.4769−10.1340i,λ3=10.9537.λ1和λ2为一对共轭复根,λ3为正实数,故平衡点S1是不稳定的鞍焦点.

同理,可求出在S3(−3.9129,−0.4053,5.1036)处的特征值为λ1=−10.4769+10.1340i,λ2=10.4769−10.1340i,λ3=10.9537.平衡点S3和S2具有相同的特征值,故S3也是不稳定的鞍焦点.

2.2.4 Lyapunov指数和分数维

众所周知,Lyapunov指数是分析动力系统非线性行为的一种方法,实际上它测量了相空间中运动轨迹的收敛或发散的指数率.如果系统至少有一个Lyapunov指数是正的,那么该系统可以被视为混沌系统.当初始状态为(u,v,w)=(1,1,1),且系统参数a=8,b=5,c=3,d=100000,e=12时,得到如图2所示的系统(1)的Lyapunov指数谱,相应的Lyapunov指数值分别是LE1=1.3078,LE2=−0.0011028,LE3=−11.3067.

图2 系统(1)的Lyapunov指数谱Fig.2.Lyapunov exponent spectrum of system(1).

此外,在Lyapunov指数谱的基础上,可以得到Lyapunov维数.Lyapunov维数的定义为

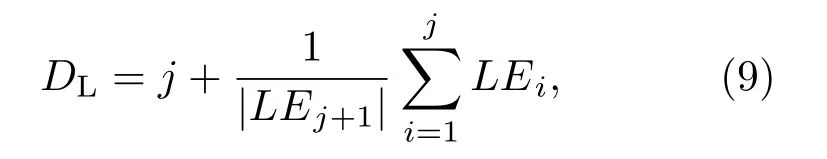
其中j是满足的最大整数.Lyapunov维数用来衡量混沌吸引子的几何标度性质或复杂性.在系统(1)中,在误差允许的范围内,LE1>0,LE2≈0,LE3<0且|LE1|<|LE3|,所以有j=2且代入(9)式,可得DL=2.1156,混沌吸引子的Lyapunov维数大于2且小于3.吸引子的分数维性质,不仅意味着该系统具有非周期轨道,而且说明了不同条件下的轨迹处于分离状态.

2.2.5 功率谱

图3为系统(1)的功率谱图,从图中可以看出,功率谱是连续的,且伴随有尖峰出现,可判定运动处于混沌状态.

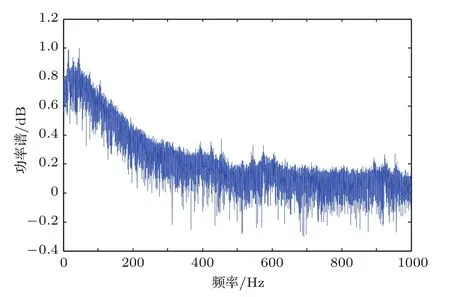
图3 系统(1)的频谱图Fig.3.Power spectrum of system(1).

3 新忆阻混沌系统在分形中的应用

本节将忆阻混沌系统与分形相结合,得到能产生多涡卷的忆阻混沌系统.数值仿真结果表明,该方法是可行的和有效的.与其他产生多涡卷混沌吸引子的方法相比,通过分形过程产生的多涡卷混沌吸引子的方法,能较好地调整混沌系统的涡卷数.

3.1 通过Julia分形产生的多涡卷混沌系统

在Julia分形式中,Zn=xn+iyn,Zn+1=xn+1+iyn+1和Z0=x0+iy0都是复数,Z0是复常数.这里先不讨论Z0,本文将在3.5节统一讨论复常数Z0.则有

在三维坐标系(u,v,w)的u和v之间加入分形过程,即在映射(x,y,z)→(x2−y2,2xy,z)中,令u=x2−y2,v=2xy,w=z,则有

得到关于x,y,z的系统方程为

将方程(1)代入(12)式中,有

得到产生多涡卷混沌系统方程为

图4为系统参数a=8,b=5,c=3,d=100000和e=12时系统(14)的相图.

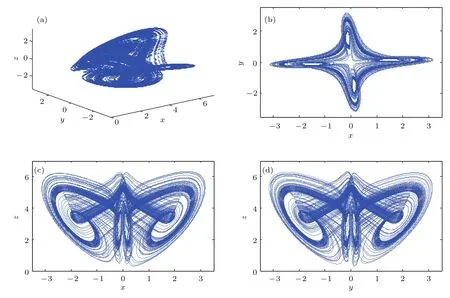
图4 系统(14)的混沌吸引子 (a)三维图;(b)x-y平面;(c)x-z平面;(d)y-z平面Fig.4.Attractor of system(14):(a)Three-dimensional view;(b)x-y plane;(c)x-z plane;(d)y-z plane.

3.2 带系数的变形Julia分形产生的多涡卷混沌系统

现在,考虑给Julia分形表达式的项乘以一个系数k,得到一个变形的Julia分形:

此时,映射矩阵为

采用与3.1节相同的方法,得到新的混沌系统方程:

图5为系统参数a=8,b=5,c=3,d=100000和e=12,k取不同值时,系统(17)在x-y平面的相图.此时,k均取正实数.从图5可以看出,k的不同取值只会改变混沌吸引子的尺寸大小,不会改变吸引子的形状,且k越大时,系统(17)相图的尺寸越小,吸引子越聚合.

3.3 高阶Julia分形产生的多涡卷混沌系统

在Julia分形修改为得到广义高阶Julia分形

考虑m>3,则3.1节中的映射变为(x,y,z)→(Re[(x+iy)m],Im[(x+iy)m],z),且有u=Re[(x+iy)m],v=Im[(x+iy)m],w=z,故产生多涡卷混沌吸引子的系统方程为

这里分别为

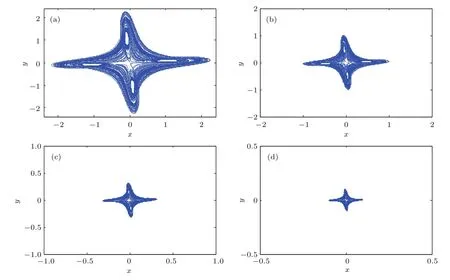
图5 k取不同值时系统(17)在x-y平面的相图 (a)k=2;(b)k=10;(c)k=100;(d)k=1000Fig.5.Chaotic attractors at x-y plane of system(17)at the different parameter k:(a)k=2;(b)k=10;(c)k=100;(d)k=1000.

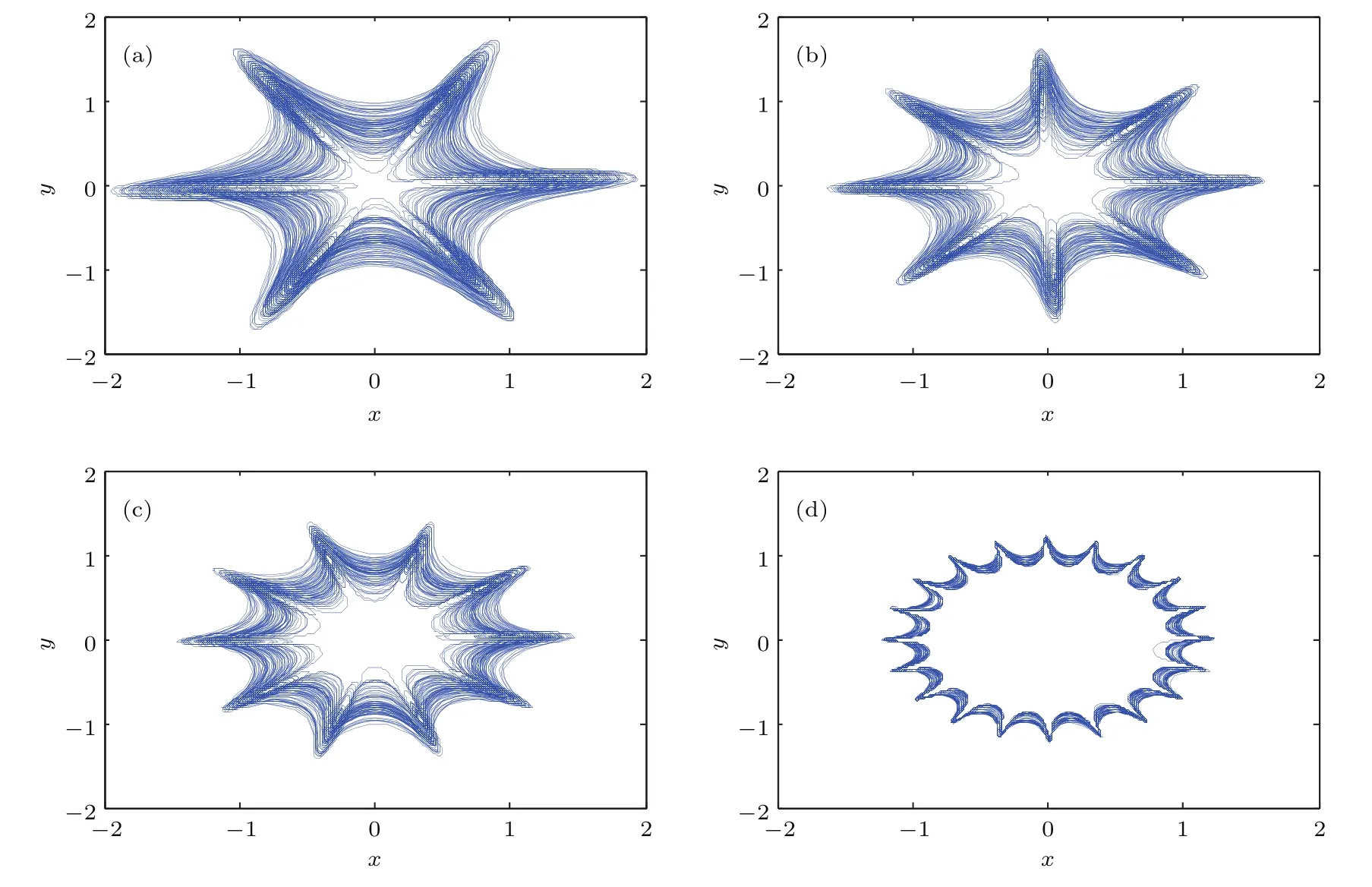
图6 多涡卷混沌系统的吸引子 (a)m=3时,6涡卷混沌系统;(b)m=4时,8涡卷混沌系统;(c)m=5时,10涡卷混沌系统;(d)m=10时,20涡卷混沌系统Fig.6.Attractors of multi-scroll chaotic system:(a)m=3,a 6-scroll chaotic system;(b)m=4,a 8-scroll chaotic system;(c)m=5,a 10-scroll chaotic system;(d)m=10,a 20-scroll chaotic system.

u和v的完整表达式为大量的仿真结果表明,当m取大于1的正整数时,都能得到多涡卷混沌系统.图6为系统参数a=8,b=5,c=3,d=100000和e=12时,m分别取3,4,5,10时,(19)式所表示的混沌系统在x-y平面的吸引子图.

3.4 多项式Julia分形产生的多涡卷混沌系统

在Julia分形的基础上,把分形迭代式更改为多项式形式:

其中运用相同的方法,将此迭代关系式应用于系统(1)中.为了更好地研究项在迭代式中的作用,进而影响通过(24)式所产生的多涡卷混沌系统,简单起见,取pj=1/L,即p1=p2=···pL=1/L.与前面3.1节、3.2节和3.3节的讨论类似,先不考虑Z0对系统的影响,即令Z0=0.关于Z0对系统的影响,统一在3.5节中讨论.下面对L取不同值时的新混沌系统进行仿真,图7为L取不同值时的多涡卷混沌吸引子在x-y平面相图.

仔细观察上面的迭代(24)式,不难发现,pj的取值也对产生的多涡卷混沌系统有较大影响.当p1=1时,对于2jL,都有pj=0,通过分形产生的混沌系统即为原始系统(1).当p2=1时,对于1jL且j2都有pj=0,通过分形产生的系统就是3.1节中的系统(14).当3kL,k∈N+,pk=1时,对于1jL且jk,都有pj=0,这就和3.3节系统(19)相同(此时,3.3节中的参数m就相当于这里的参数k).

3.5 复常数Z0对系统的影响

前文主要讨论了Julia分形中指数项的作用,让Z0=0.本节着重讨论复常数Z0取不同值时,对混沌系统的影响.考虑Z0=x0+iy00,将它代入u和v的表达式中,更新u和v的值.

对于3.1节的u和v,有

对于3.2节的u和v,有

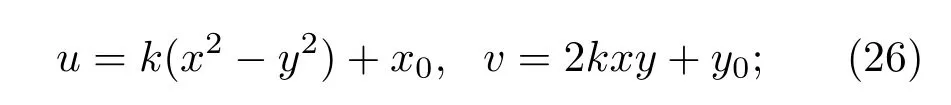
在3.3节中,就有

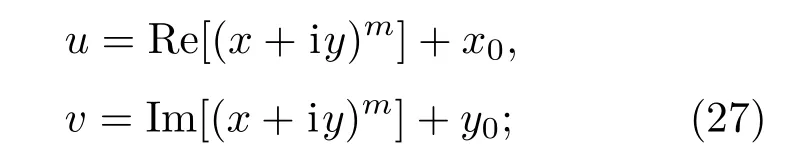
同理,对于3.4节中的u和v,有

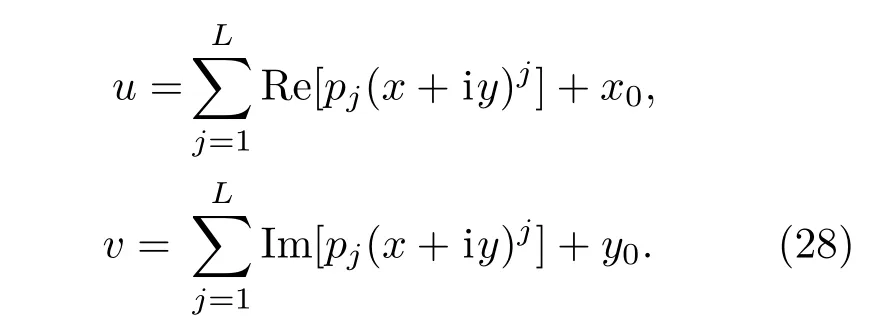
这里,同样取pj=1/L,j=1,2,···,L.图8反映了Z0取不同值时,对混沌系统的影响.

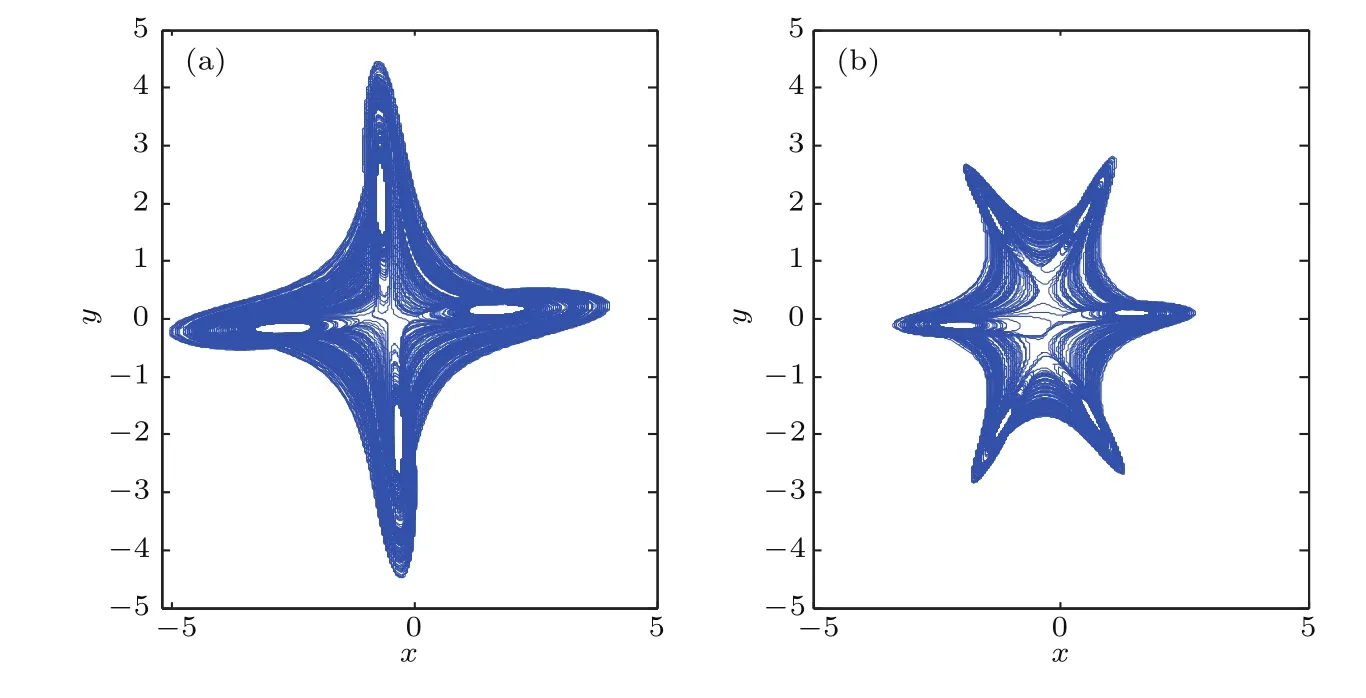
图7 L取不同值时的混沌吸引子 (a)L=2;(b)L=3Fig.7.The chaotic attractors at x-y plane with different L:(a)L=2;(b)L=3.

图8 Z0取不同值时,系统在x-y平面的相图 (a)(25)式,Z0=1+0.5i;(b)(26)式,k=2,Z0=3−0.1i;(c)(27)式,m=3,Z0=−3.5−1.2i;(d)(28)式,L=3,p=1/3,Z0=−1+0.5iFig.8.Chaotic attractors at x-y plane with different Z0:(a)Eq.(25),Z0=−1+0.5i;(b)Eq.(26),k=2 and Z0=3−0.1i;(c)Eq.(27),m=3 and Z0=−3.5−1.2i;(d)Eq.(28),L=3,p=1/3,Z0=−1+0.5i.

4 结 论

忆阻器作为一种体积小、功耗低的新型元件,在混沌电路中有着较高的应用价值.本文新构建了一个基于磁控二氧化钛忆阻器的三维忆阻混沌系统,通过分析系统的对称性、耗散性、平衡点稳定性、功率谱、Lyapunov指数和分数维,对系统动力学特性进行了分析,从而验证了系统的混沌特性.此外,本文还尝试着将经典的Julia分形过程及其变形应用于混沌系统中,产生了丰富的多涡卷混沌吸引子,不仅弥补了通过功能函数产生多涡卷混沌吸引子的不足,而且其涡卷数能随着某些参数的变化而变化.改变Julia分形及其变形中复常数的值,能得到不同形状的混沌吸引子.这也为进一步研究分形与混沌系统的结合提供了参考.

参考文献

[1]Chua L O 1971IEEE Trans.Circ.Theor.18 507

[2]Strukov D B,Snider G S,Stewart D R,Williams R S 2008Nature453 80

[3]Zhou J,Huang D 2012Chin.Phys.B21 048401

[4]Wang L D,Li H F,Duan S K,Huang T W,Wang H M 2016Neurccomputing171 23

[5]Min G Q,Wang L D,Duan S K 2015Acta Phys.Sin.64 210507(in Chinese)[闵国旗,王丽丹,段书凯 2015物理学报64 210507]

[6]Mandelbrot B B 1967Science156 636

[7]Mandelbrot B B 1975Fractals:Form,Chance and Dimension(San Francisco:WH Freeman and Company)pp35–37

[8]Li H Q,Wang F Q 1999Fractal Theory and Its Application in Molecular Science(Beijing:Science Press)p33(in Chinese)[李后强,汪富泉1999分形理论及其在分子科学中的应用(北京:科学出版社)第33页]

[9]Lorenz E N 1963J.Atmos.Sci.20 130

[10]Chua L O,Komuro M,Matsumoto T 1986IEEE Trans.Circ.Syst.33 1072

[11]Chen G R 1999Int.J.Bifurcat.Chaos9 1465

[12]Wang L D,Drakakis E,Duan S K,He P F,Liao X F 2012Int.J.Bifurcat.Chaos22 1250205

[13]Muthuswamy B,Kokate P P 2009IETE Tech.Rev.26 417

[14]Zhou Z W,Su Y L,Wang W D,Yan Y 2017J.Petrol.Explor.Prod.Technol.7 487

[15]Bouallegue K 2015Int.J.Bifurcat.Chaos25 1530002

[16]Chua L O,Roska T 1993IEEE Trans.Circ.Syst.I40 147

[17]Yalcin M,Suykens J,Vandewalle J,Ozoguz S 2002Int.J.Bifurcat.Chaos12 23

[18]Tang W K S,Zhong G Q,Chen G,Man K F 2001IEEE Trans.Circ.Syst.I48 1369

[19]Zarei A 2015Nonlinear Dyn.81 585

[20]More C,Vlad R,Chauveau E 2010Nonlinear Dyn.59 45

[21]Huan S M,Li Q D,Yang X S 2012Nonlinear Dyn.69 1915

[22]Lü J H,Yu X H,Chen G R 2003IEEE Trans.Circ.Syst.I50 198

[23]Yalcin M,Suykens J,van de Walle J 2005Chaos Modeling and Control Systems Design(Singapore:World Scienti fic)p59

[24]Lü J H,Chen G R,Yu X H,Leung H 2004IEEE Trans.Circ.Syst.I51 2476

[25]Lü J H,Yu S M,Leung H,Chen G R 2006IEEE Trans.Circ.Syst.I53 149