具有早期后除极化现象的可激发系统中螺旋波破碎方式研究∗

韦宾 唐国宁 邓敏艺

(广西师范大学物理科学与技术学院,桂林 541004)

1 引 言

螺旋波是各种反应扩散系统中普遍存在的一种非平衡斑图[1],例如在各种生物系统[2−4]、物理系统[5,6]、化学系统[7]都观察到螺旋波.与靶波不同,螺旋波不需要持续的外部刺激来维持,它是一种自维持波.由于心脏中螺旋波的频率比自然心跳的频率要高很多,所以心脏出现螺旋波电信号会导致心室心动过速,如果心脏中螺旋波破碎形成时空混沌,心室心动过速将发展为心室纤维性颤动,危及生物体的生命[3],因此心脏系统中螺旋波动力学、螺旋波破碎机制及螺旋波控制的研究已成为斑图动力学研究的热点问题[8−10].

研究表明:心脏的螺旋波有多种破碎机制,如陡峭的动作电位恢复曲线、2:1响应(两次刺激有一次响应)、超常的传导速度等[11],这些破碎机制没有涉及心脏中的重要现象——早期后除极化,因此是不够全面的.早期后除极化是心肌细胞跨膜电位在复极阶段出现多次振荡的现象,早期后除极化在心室心动过速到心室纤维性颤动的转变过程中扮演重要角色[12],所以早期后除极化也会导致螺旋波破碎[13].由于在长QT综合征和心力衰竭情况下早期后除极化是一种重要的引起致命性心律失常的原因[14],所以早期后除极化的产生机制及其如何引起心颤已引起人们极大的关注[15−19].研究发现,早期后除极化能在波向前传播的过程中产生向后传播的波[16],我们把这种现象称为回火效应,所产生的波称为回火波.到目前为止,早期后除极化如何导致螺旋波破碎仍缺乏足够研究,而这些研究有助于掌握致命性心律失常产生机制.

本文采用可激发Greenberg-Hasting(GH)元胞自动机模型[20],研究了早期后除极化如何导致螺旋波的破碎.数值模拟结果表明:早期后除极化既可以产生向前传播的波,也可以产生向后传播的波,因此对稳定螺旋波有重要的影响.这些影响包括:早期后除极化使螺旋波漫游、漂移、波臂发生形变、波臂发生折断以及导致螺旋波破碎和消失等.在某些情况下,早期后除极化起到避免螺旋波破碎的作用,甚至还能使即将消失的螺旋波得以恢复,而在另一些情况下,早期后除极化则促使螺旋波发生各种方式的破碎,总结为8种方式.这些破碎方式由于与早期后除极化的激发有关,所以与目前已经发现的螺旋波破碎方式都不相同,并得到了螺旋波破碎比率与医学调查结果基本一致的结果.下面先介绍本文使用的模型,然后介绍模拟结果与分析,最后是结论.

2 模 型

在本文采用的二维可激发GH元胞自动机模型中,可激发元胞均匀分布在正方点阵上形成可激发介质,相邻元胞间距为1,系统大小为N×N=300×300个格点,元胞在正方点阵上的位置用坐标(i,j)来表示,其t时步状态用ui,j(t)表示,采用扩展Moor邻居,元胞邻域半径为r,元胞状态总数为n,元胞(i,j)的状态ui,j(t)在集合{0,1,···,n−1}中取值,ui,j(t)=0表示静息态,ui,j(t)=1表示激发态,ui,j(t)=2,3,···,n−1表示不应态.元胞状态的演化规则如下[20]:

式中mod表示求余,Mi,j表示处于静息态的元胞(i,j)的邻域内有Mi,j个元胞处在激发态(包括发生早期后除极化的态),k表示激发阈值.为了引入早期后除极化,本文考虑两种元胞:一种是正常元胞,用于代表正常细胞,其状态数固定取n=7;一种是老化元胞,用于代表老化细胞.考虑到细胞老化后其体型会出现肥大,导致心脏肥大,心室肥大又会引起细胞出现早期后除极化和动作电位的延长[21],因此将老化元胞的状态数固定取n=12.老化元胞与正常元胞不同之处是:当老化元胞处于早期后除极化状态ui,j(t)=m>3(m表示早期后除极化态)时发生早期后除极化,元胞处于早期后除极化态ui,j(t)=m与处于激发态ui,j(t)=1同样具有激发其他元胞的能力,两种元胞的演化规则都是方程(1),计算Mi,j时都要考虑邻域半径内元胞处于早期后除极化态的数目.

在下面的数值模拟中,老化元胞被均匀地分布在正方点阵上,老化元胞与总元胞之比ρ称为老化元胞密度.心脏老化程度越高,老化细胞密度就越大,细胞老化程度越高,其激发性就越低.本文将老化元胞密度ρ、元胞邻域半径r、激发阈值k、早期后除极化态m视为可调参数:分别取ρ=1/4,1/2和3/4;邻域半径r在[3,5]范围变化;激发阈值k在[1,19]范围变化;关于早期后除极化态m,考虑两种类型的早期后除极化,即相II型和相III型早期后除极化,它们分别对应动作电位处于II期和III期阶段时细胞出现早期后除极化,这时分别取m等于4和9与之对应,m=4表示在细胞处于动作电位第II期(元胞处于4态)出现一次除极化,m=9表示在细胞处于动作电位第III期(元胞处于9态)出现一次除极化.在实际中也可能存在细胞在动作电位II期复极化过程中膜电位出现多次振荡,这种情况用在元胞分别处于4态和6态各出现除极化来表示,记为m=4,6,因此当这种元胞处于4态和6态都可以对中心细胞有激发作用.所有数值模拟采用无流边界条件,在边界附近元胞邻域半径逐渐降为1,相应的激发阈值等比例减少.

3 数值模拟结果

在下面的数值模拟中,都是首先在只考虑正常元胞和给定r和k下,在系统中产生初态螺旋波,然后考虑早期后除极化(即引入老化元胞),同时认为两种元胞的r和k值相同.图1给出了在不同m和ρ的情况下k-r参数平面上的相图,图中空白处表示不能产生初态螺旋波.从图1可以看出,存在早期后除极化对螺旋波不产生影响和对螺旋波产生各种影响两种情况,各种影响包括较轻的影响(只导致螺旋波漫游、漂移、波臂发生形变等)和较严重影响(导致螺旋波破碎和消失),在333组参数中有88组参数螺旋波不受早期后除极化影响,不受影响比率约为26.4%.螺旋波不受影响的原因是:一种元胞维持的螺旋波可以正常传播且动力学行为没有发生任何变化,而另一种元胞维持的波不能独立传播,这时系统只有一个螺旋波,不出现双螺旋波.

当只有相II型早期后除极化(m=4,6)时,在波传播过程中,早期后除极化一般只会产生回火波,因为两种元胞同时被激发后,当老化元胞处于早期后除极化态时,正常元胞还没有回到静息态,所以只有当两种元胞不同时被激发,正常元胞已经处于静息态并遇到老化元胞的后除极化态,才能产生向前传播的波.但是相III型早期后除极化的激发作用既可以产生向前传播的波,也可以产生向后传播的波,因为这种情况下,老化元胞回到静息态所需时间是正常元胞的近两倍,因此早期后除极化会对螺旋波产生各种影响,例如引起螺旋波漫游、漂移、波臂发生形变以及导致螺旋波破碎和消失等,如图1所示.另一方面,老化元胞的早期后除极化也有维持螺旋波的作用,例如图1(h)中参数(k=7,r=3)对应着螺旋波破碎为无规则的波,但在老化元胞密度增大后的图1(i)中参数(k=7,r=3)却对应着螺旋波不发生破碎,显然增加具备早期后除极化作用的元胞数量起到了维持螺旋波的作用,可见早期后除极化一方面会破坏螺旋波的稳定性,另一方面也起到维持螺旋波的作用,这一维持作用的机制是:增大的老化细胞密度减少了元胞状态数的离散性,从而能维持螺旋波不破碎.

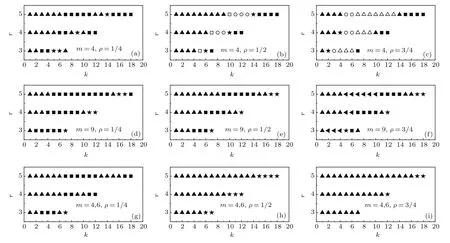
图1 不同m和ρ值下r-k参数平面上的相图(代表螺旋波几乎不受早期后除极化影响;代表螺旋波受早期后除极化的影响较轻;⋆代表螺旋波已经破碎成无规波或多螺旋波;?代表螺旋波先停止旋转,在螺旋波转变为反靶波后消失;◦代表螺旋波波臂先出现断裂,在螺旋波转变为反靶波后消失;△代表螺旋波由于传导障碍直接消失;代表整体传导障碍导致螺旋波破碎成螺旋状波)Fig.1.Phase diagram in the r-k parameter plane for different values of m and ρ.Black square,spiral wave is not a ff ected by early afterdepolarization(EAD);black up-triangle,spiral wave is a ff ected by EAD slightly;black star,spiral wave breaks up into irregular wave or multiple spiral waves;hollow square,spiral wave first stops its rotation and then disappears after phase transition from spiral wave to anti-target wave;hollow circle,spiral arm first breaks and then disappears after phase transition from spiral wave to anti-target wave;hollow up-triangle,spiral wave disappears because of conduction block;black left triangle,global conduction block causes spiral waves to break up into an un-rotated spiral wave.

通常,早期后除极化对螺旋波影响包括以下6种情况:1)回火波的干扰使螺旋波波臂变形或波臂局部出现折断;2)间歇式出现双螺旋波,它们分别由老化元胞和正常元胞维持,因为两种元胞的状态数不同,有些情况还伴随回火波和早期后除极化激发产生向前传播的波的干扰;3)在老化元胞密度比较小的情况下,正常元胞维持的螺旋波不受影响,而老化元胞维持的螺旋波发生破碎,形成无规波形;4)在老化元胞密度比较大的情况下,老化元胞维持的螺旋波不受影响,而正常元胞维持螺旋波发生沿对角线断开;5)导致螺旋波漫游或漂移,图2显示螺旋波沿对角漂移,从图2可以看出,初态螺旋波的周期大于老化元胞的状态数,使得两种元胞始终同时被激发,所以早期后除极化不会导致双螺旋波的出现,由于螺旋波存在小幅度漫游,间歇出现u=1的等高线与u=4的等高线相交情况,这时早期后除极化参与激发作用,增加了螺旋波波头的旋转速度,从而使螺旋波沿对角线来回漂移;6)导致螺旋波消失.下面重点探讨早期后除极化导致的螺旋波消失和破碎情况.

图2 在ρ=1/4,m=4,r=3,k=7的情况下不同时刻元胞状态斑图 (a)t=0;(b)t=1000;(c)t=2100;(d)t=3100Fig.2.Patterns of cellular states at different time moments for ρ=1/4,m=4,r=3 and k=7:(a)t=0;(b)t=1000;(c)t=2100;(d)t=3100.

图3 在ρ=1/2,m=4,r=3,k=5的情况下不同时刻元胞状态斑图 (a)t=0;(b)t=17;(c)t=96;(d)t=240Fig.3.Patterns of cellular states at different time moments for ρ=1/2,m=4,r=3 and k=5:(a)t=0;(b)t=17;(c)t=96;(d)t=240.

图1中符号“⋆”和对应螺旋波破碎情况,可以看出:在各种老化元胞密度下,系统都可能会出现螺旋波破碎,333组参数中有46组参数(符号“⋆”和“”对应的参数)发生破碎,螺旋波发生破碎的总比率约为13.8%.从图1还可以看出,在给定老化元胞密度和早期后除极化态的情况下,螺旋波破碎的比率一般是比较低的,在37组参数中一般只有1到5组参数出现螺旋波破碎,破碎比率介于2.7%—13.5%之间,但是在特定的老化元胞密度和早期后除极化态的情况下,如图1(f)和图1(h)所示,螺旋波破碎的比率会大为增加:图1(f)的37组参数中有15组参数会出现螺旋波破碎,破碎比率达到40.5%;图1(h)的37组参数中有9组参数出现螺旋波破碎成无规则斑图,破碎比率达到24.3%.图1(f)和图1(h)给出的螺旋波破碎比率平均约为32.4%,而且螺旋波破碎的速度都很快,人的心脏中出现这种快速破碎情况将会危及生命.

Andreoli等[23]调查了70个具有自发蛛网膜下腔出血病例,他们发现91%的病例存在心律失常,其中41%的病人有严重的心律失常,在这些严重的心律失常病人中有10.34%出现室颤.图1(a)和图1(e)给出了螺旋波破碎比率为4/37=10.8%,接近Andreoli等[23]的调查结果.Reinelt等[24]调查了心律失常的发病率,他们发现心律失常死亡率约为30.8%.Huikuri等[25]调查了心律失常导致的突然死亡,他们发现,若病人有心梗和心室心动过速病史,猝死率达到约31.6%.本文得到在图1(f)和图1(h)给出的后除极化和老化元胞的密度情况下,螺旋波的平均破碎比率约为32.4%,与这些调查结果基本一致.这些结果说明,本文提出的模型是合理的.在特定情况下,螺旋波破碎比率高,可以解释心律失常导致死亡率高的现象,因此用简单的模型探讨早期后除极化导致螺旋波破碎的方式,有助于人们了解早期后除极化如何导致室颤以及怎样的早期后除极化危害较大.下面通过元胞状态斑图介绍在早期后除极化作用下螺旋波的不同破碎方式,给出的所有元胞状态斑图都为灰度图,元胞状态值越大,对应的点就越明亮.

第1种螺旋波破碎方式是:螺旋波从中心区开始破碎,但不是纯多普勒效应(螺旋波波头漫游)引起的,还与早期后除极化的激发有关.图1(a)中符号“⋆”就是指这种方式的螺旋波破碎.图4给出了在ρ=1/4,m=4,r=3,k=5的情况下不同时刻的元胞状态斑图,可以看出,由于两种元胞的状态数不同,正常元胞回到静息态时,老化元胞还没有回到静息态,导致老化元胞间歇被激发,使得螺旋波波头位置的激发性不足,螺旋波出现间歇性停止旋转,波头发生漂移,使得螺旋波中心区域的波比较稀疏.由于老化元胞间歇被激发,老化元胞维持的螺旋波会破碎,出现正常元胞与老化元胞不同步激发现象,这时不断出现处于静息态的正常元胞遇到老化元胞的后除极化态而被激发,图4(c)显示的圆形波就是这样产生的.圆形波与原螺旋波波臂碰撞,导致螺旋波破碎成多螺旋波,而且螺旋波破碎时间较长.如果取图1(a)中(r,k)=(3,6),(4,9),(5,14)这3组参数及图1(d)中(r,k)=(3,7)这组参数和图1(f)中(r,k)=(3,5)这组参数去模拟,也可观察到螺旋波从中心开始破碎.

图4 在ρ=1/4,m=4,r=3,k=5的情况下不同时刻元胞状态斑图 (a)t=0;(b)t=26;(c)t=58;(d)t=86;(e)t=262;(f)t=1000Fig.4.Patterns of cellular states at different time moments for ρ=1/4,m=4,r=3 and k=5:(a)t=0;(b)t=26;(c)t=58;(d)t=86;(e)t=262;(f)t=1000.

第2种螺旋波破碎方式是:螺旋波从外围开始破碎,但这种破碎不是爱克豪斯失稳引起的.图5给出了在ρ=1/4,m=9,r=4,k=11的情况下不同时刻的元胞状态斑图,可以看出,首先在边界出现回火波向介质中心传播,它们与原螺旋波波臂碰撞,进而导致早期后除极化产生环状波,使螺旋波从其外围开始破碎,并向中心扩散,最后导致整个螺旋波破碎.在图1(d)和图1(i)中取r>3的螺旋波破碎参数,在图1(b)中取(r,k)=(4,10)这组参数和在图1(c)中取(r,k)=(3,2),(4,4)这两组参数去模拟,都观察到了螺旋波从外围开始破碎.

第3种螺旋波破碎方式是:非对称破缺导致螺旋波破碎.图6给出了在ρ=1/2,m=4,r=3,k=6的情况下不同时刻的元胞状态斑图,其中第一排图的初态螺旋波是顺时针旋转,第二排图的初态螺旋波是逆时针旋转.从图6可以看出,由于介质激发性不足,螺旋波首先停止旋转,之后螺旋波发生非对称破缺,对于不同的初态螺旋波旋转方向,螺旋波波臂断开的位置不同,在螺旋波残臂向边界运动的过程中,回火波与之碰撞,最后都形成多螺旋波.

图5 在ρ=1/4,m=9,r=4,k=11的情况下不同时刻螺旋波斑图 (a)t=0;(b)t=33;(c)t=146;(d)t=704Fig.5.Patterns of cellular states at different time moments for ρ=1/4,m=9,r=4 and k=11:(a)t=0;(b)t=33;(c)t=146;(d)t=704.

图6 在ρ=1/2,m=4,r=3,k=6的情况下不同时刻元胞状态斑图 (a),(d)t=0;(b),(e)t=15;(c),(f)t=200Fig.6.Patterns of cellular states at different time moments for ρ=1/2,m=4,r=3 and k=6:(a),(d)t=0;(b),(e)t=15;(c),(f)t=200.

第4种螺旋波破碎方式是:对称破缺导致螺旋波破碎.图7给出了在ρ=1/2,m=4,r=5,k=14的情况下不同时刻的元胞状态斑图,可以看出:初态螺旋波波长比较长,但是波前与波后距离为三个时步内波传播的距离,由于两种元胞状态数不同,所以经过3个时步,出现老化元胞维持的波遇到不应态元胞,导致老化元胞无法被激发;在第6时步,空间出现两块静息态区,一块只有正常元胞处于静息态,称为A区,该区域与老化元胞的第7态至10态重叠,对应为图7(b)中的亮区域,另一块区是只有老化元胞处于静息态,称为B区,该区域与正常元胞的第3态重叠,对应图7(b)中的暗区域,正常元胞的激发态与老化元胞的第11态重叠,对应图7(b)的最亮区域;在第7时步正常元胞激发B区内的元胞,A区只有轴线附近的元胞被激发,这些被激发的元胞形成向外传播的波;由于介质的各向异性,正常元胞维持的螺旋波沿对角线方向的波臂逐渐变细,如图7(c)所示;在第15时步出现回火波,回火波与向外传播的波相碰,导致螺旋波沿轴线折断,这些折断的波臂不会演变为螺旋波而是重新接上,在第二次出现回火波后,螺旋波开始沿对角线折断,折断处部分形成新的螺旋波,它们最终使螺旋波破碎成多螺旋波,如图7(d)所示.如果取图1(e)中(r,k)=(3,7)这组参数和图1(h)中(r,k)=(3,6),(4,10),(5,15)这3组参数去模拟,同样观察到了螺旋波对称破缺导致的破碎,如图8所示.

图7 在ρ=1/2,m=4,r=5,k=14的情况下不同时刻元胞状态斑图 (a)t=0;(b)t=6;(c)t=14;(d)t=35;(e)t=52;(f)t=344Fig.7.Patterns of cellular states at different time moments for ρ=1/2,m=4,r=5 and k=14:(a)t=0;(b)t=6;(c)t=14;(d)t=35;(e)t=52;(f)t=344.

图8 在ρ=1/2,m=9,r=3,k=7的情况下不同时刻元胞状态斑图 (a)t=0;(b)t=26;(c)t=302;(d)t=917Fig.8.Patterns of cellular states at different time moments for ρ=1/2,m=9,r=3 and k=7:(a)t=0;(b)t=26;(c)t=302;(d)t=917.

第5种螺旋波破碎方式是:早期后除极化激发不断同时产生两个沿相反方向传播的波,最终导致螺旋波破碎,我们称这种破碎为同时激发双波导致的破碎,如图9所示.从图9可以看出,初态螺旋波的波长很长,表明元胞停留在静息态的时间很长,加入老化细胞后,出现每9个时步早期后除极化激发同时产生沿相反方向传播的两个波,向前传播的波由正常元胞维持(由于被老化元胞维持的波掩盖而看不清),向后传播的波则由两种元胞维持(图9中与亮区相邻的暗区就是刚产生的回火波),激发态激发的波与早期后除极化激发的波相互作用,最后导致螺旋波破碎成无规则波.取图1(e)和图1(f)中r>3下螺旋波破碎参数去模拟,都观察到了这类破碎.

第6种螺旋波破碎方式是:早期后除极化在非对称位置产生向边界传播的波,这些波与原螺旋波相互作用导致螺旋波破碎,我们称这种破碎方式为非对称激发导致的破碎,如图10所示.图10显示,初态螺旋波呈方形,说明初态螺旋波沿轴线方向传播速度快;最初早期后除极化在右侧和下方分别不断产生了向外传播的小波,与原螺旋波波臂发生碰撞导致螺旋波的波臂折断,在经过29个时步后,在螺旋波中心区域,早期后除极化在各个方向上不断产生向外传播的小波,它们与元胞激发态激发的波碰撞,最后导致螺旋波破碎.在螺旋波最初的演化中,早期后除极化没有产生回火波的原因是:回火波是向中心传播,波长会缩短,从而导致激发不足而无法传播.

在数值模拟中发现,改变初态螺旋波的朝向和初态螺旋波旋转方向,都会改变早期后除极化产生小波的位置,这表明在螺旋波态下,早期后除极化的激发作用导致的螺旋波破碎与初态螺旋波旋转方向和初态螺旋波朝向都有关.

图9 在ρ=3/4,m=9,r=5,k=18的情况下不同时刻螺旋波斑图 (a)t=0;(b)t=15;(c)t=114;(d)t=348Fig.9.Patterns of cellular states at different time moments for ρ=3/4,m=9,r=5 and k=18:(a)t=0;(b)t=15;(c)t=114;(d)t=348.

图10 在ρ=1/4,m=4,6,r=3,k=7的情况下不同时刻螺旋波斑图 (a)t=0;(b)t=21;(c)t=75;(d)t=360Fig.10.Patterns of cellular states at different time moments for ρ=1/4,m=4,6,r=3 and k=7:(a)t=0;(b)t=21;(c)t=75;(d)t=360.

第7种螺旋波破碎方式是:整体传导障碍导致螺旋波破碎成不旋转的螺旋波,如图11所示,图11(b)—(d)会持续交替出现.从图11可以看出,初态螺旋波是稠密螺旋波,波长短,加入老化元胞后,老化元胞维持的螺旋波传播遇到不应态老化元胞,导致老化元胞不被激发,斑图开始变暗.但是正常元胞维持的螺旋波可正常传播.在第10时步,处于静息态的老化元胞遇到处于激发态的正常元胞,老化元胞被再次激发,但是这时在螺旋波波头附近出现两块分离的静息态区,这些区域的元胞被激发后干扰了螺旋波波头附近波的传播,导致正常元胞维持的螺旋波从中心开始破碎,最终导致其完全破碎.当老化元胞维持的螺旋波再次出现传导障碍后,螺旋波开始变暗,直到早期后除极化在螺旋波中心区的激发作用恢复螺旋波的传播,这时螺旋波中心区逐渐变亮,而其外围仍为暗区.当中心处的波传播到外围时,螺旋波外围开始变亮,同时螺旋波中心区开始变暗(传导障碍导致),直到早期后除极化在螺旋波中心区的激发作用恢复螺旋波传播.老化元胞维持的螺旋波区域明暗交替的过程周而复始地进行.由于这个螺旋波是早期后除极化产生的,因此螺旋波是不旋转的,就出现图11所示的现象,图1(f)中符号“”所指的破碎就是这种破碎.这些结果表明,早期后除极化的激发作用也有避免螺旋波消失的作用.

第8种螺旋波破碎方式是:初期出现双螺旋波,其中一个螺旋波的波臂出现沿对角线折断,之后在早期后除极化激发的波与激发态激发的波相互作用下,螺旋波整体快速破碎,如图12所示,图1(h)中符号“⋆”所指的螺旋波破碎基本就是这种破碎方式(除3组与符号“”相邻的参数外),我们称这种破碎为整体快速破碎.

从上述螺旋波破碎方式的机制可以看出,对于不同早期后除极化态和不同老化元胞密度,在适当的元胞激发阈值下都会导致螺旋波破碎,而且虽然破碎方式不尽相同,但是所有螺旋波破碎方式都与早期后除极化的激发作用有关,这表明早期后除极化有促进螺旋波破碎的作用,这与文献[12]的结论一致.同时也可看到,在m=9和ρ=3/4的情况下,早期后除极化也起到维持螺旋波的作用.

图11 在ρ=3/4,m=9,r=4,k=6的情况下不同时刻螺旋波斑图 (a)t=0;(b)t=74;(c)t=80;(d)t=86Fig.11.Patterns of cellular states at different time moments for ρ=3/4,m=9,r=4 and k=6:(a)t=0;(b)t=74;(c)t=80;(d)t=86.

图12 在ρ=1/2,m=4,6,r=3,k=7的情况下不同时刻螺旋波斑图 (a)t=0;(b)t=13;(c)t=21;(d)t=30Fig.12.Patterns of cellular states at different time moments for ρ=1/2,m=4,6,r=3 and k=7:(a)t=0;(b)t=13;(c)t=21;(d)t=30.

4 结 论

采用二维可激发GH元胞自动机模型,研究了早期后除极化引起的螺旋波破碎方式.数值模拟结果显示,早期后除极化的激发作用既可以激发向前传播的波,也可以激发向后传播的波,因此早期后除极化不仅可以促进螺旋波的破碎,在m=9和ρ=3/4的情况下还能避免螺旋波的消失.早期后除极化对螺旋波不产生影响的比率约为26.4%,其他大部分情况都会对螺旋波产生影响.当早期后除极化对螺旋波有较小影响时,早期后除极化只是导致螺旋波漫游、漂移和波臂发生形变等;当早期后除极化对螺旋波有严重影响时,早期后除极化会导致螺旋波消失和破碎.螺旋波消失方式有两种,即通过传导障碍直接消失或转变为反靶波后消失,消失总比率约为7.8%.本文观察到8种新的螺旋波破碎方式,包括始于螺旋波中心的破碎、始于螺旋波外围的破碎、非对称破缺导致的破碎、对称破缺导致的破碎、同时激发双波导致的破碎、非对称激发导致的破碎、整体传导障碍导致的破碎、整体快速破碎.分析发现,这8种新的螺旋波破碎方式都与早期后除极化激发产生的回火波有关;此外,还发现在某些老化元胞密度值和早期后除极化态的情况下,早期后除极化导致螺旋波破碎的比率比较小,介于2.7%—13.5%之间,但在适当选择参数(m,ρ,r,k)的情况下,螺旋波破碎的比率比较大,平均比率可高达32.4%,这表明螺旋波破碎与系统老化元胞密度、早期后除极化类型都有密切关系.由于在m=9和ρ=3/4以及m=4,6和ρ=1/2的情况下,所得到的螺旋波破碎比率与有关心律失常致死的医学调查结果基本符合,因此本文数值模拟结果能够为医务人员正确判断早期后除极化致死率并采取有效措施提供有用信息.

参考文献

[1]Cross M C,Hohenberg P C 1993Rev.Mod.Phys.65 851

[2]Lee K J,Cox E C,Goldstein R E 1996Phys.Rev.Lett.76 1174

[3]Davidenko J M,Pertsov A V,Salomonsz R,Baxter W,Jalife J 1992Nature355 349

[4]Huang X,Xu W,Liang J,Takagaki K,Gao X,Wu J 2010Neuron68 978

[5]Plapp B B,Egolf D A,Bodenschatz E,Pesch W 1998Phys.Rev.Lett.81 5334

[6]Larionova Y,Egorov O,Cabrera-Granado E,Esteban-Martin A 2005Phys.Rev.A72 033825

[7]Müller S C,Plesser T,Hess B 1985Science230 661

[8]Liu G Q,Ying H P,Luo H L,Liu X X,Yang J H 2016Int.J.Bifurcat.Chaos26 1650236

[9]Chen J X,Guo M M,Ma J 2016EPL113 38004

[10]Chen J X,Zhang H,Qiao L Y,Liang H,Sun W G 2018Commun.Nonlinear Sci.Numer.Simulat.54 202

[11]Fenton F H,Cherry E M,Hastings H M,Evans S J 2002Chaos12 852

[12]Ashihara T,Yao T,Namba T,Kawase A,Ikeda T,Nakazawa K,Ito M 2002Circ.J.66 505

[13]Wei H M,Tang G N 2011Acta Phys.Sin.60 030501(in Chinese)[韦海明,唐国宁 2011物理学报 60 030501]

[14]Weiss J N,Gar finkel A,Karagueuzian H S,Chen P S,Qu Z L 2010Heart Rhythm.7 1891

[15]Zimik S,Vandersickel N,Nayak A R,Pan filov A V,Pandit R 2015PLoS ONE10 e0130632

[16]Vandersickel N,Kazbanov I V,Nuitermans A,Weise L D,Pandit R,Pan filov A V 2014PLoS ONE9 e84595

[17]Wang X Y,Wang P,Tang G N 2017Acta Phys.Sin.66 068201(in Chinese)[王小艳,汪芃,唐国宁2017物理学报66 068201]

[18]Vandersickel N,Nieuwenhuyse E V,Seemann G,Panfilov A V 2017Front Physiol.8 404

[19]Dutta S,Mincholé A,Zacur E,Quinn T A,Taggart P,Rodriguez B 2016Prog.Biophys.Mol.Biol.120 236

[20]Greenberg J M,Hastings S P 1978SIAM J.Appl.Math.34 515

[21]Yan G X,Rials S J,Wu Y,Liu T X,Xu X P,Marinchak R A,Kowey P R 2001Am.J.Physiol.Heart Circ.Physiol.281 H1968

[22]Du ffH J,Mitchell L B,Gillis A M,Sheldon R S,Chudleigh L,Cassidy P,Chiamvimonvat N,Wyse D C 1993Circulation88 1056

[23]Andreoli A,Di P G,Pinelli G,Grazi P,Tognetti F,Testa C 1987Stroke18 558

[24]Reinelt P,Karth G D,Geppert A,Heinz G 2001Intensive Care Med.27 1466

[25]Huikuri H V,Gastellanos A,Myerburg R J 2001N.Engl.J.Med.345 1473