基于宽带立体超透镜的远场超分辨率成像∗

高强 王晓华 王秉中

(电子科技大学应用物理研究所,成都 610054)

1 引 言

超分辨率最早应用于光学亚波长成像,即在物体近场范围内探测物体本身包含的精细结构特征所对应的高频分量来实现超分辨率[1−4].Wolf等根据光学成像过程得出如下结论:一束光入射到一个具有超精细结构(精细尺度小于半个波长)的物体上,其必然被转换成传播波和凋落波.其中,入射波既可以是传播波也可以是凋落波,传播波分量能够传播到探测器,凋落波分量只能存储在结构表面.前者与物体本身对应的低频分量相关联,后者与物体包含的精细结构对应的高频分量(亚波长信息)相关联.亚波长信息通过凋落波向外传播,而凋落波分量的幅度呈指数衰减而无法传播到远场参与成像,导致远场成像缺少大量精细结构信息,无法获得超分辨率.因此,如何获取亚波长信息(高频分量)是实现超分辨率成像的关键.在1984年,Pohl等[5]提出了利用近场探针扫描物体表面来实现亚波长成像,缺点是近场扫描光学显微镜需要消耗较长的时间来逐点扫描,因此,无法实时高效成像.随后,同时具有负介电常数和负磁导率的完美透镜被提出来,该透镜可以将凋落波幅度进行放大,然后在透镜的出射面扫描成像[6−9].其局限性是成像范围依旧处于近场范围,因为凋落波离开透镜后仍呈指数衰减.为了实现远场超分辨率成像,一种可行的方法是将凋落波转换为传播波辐射到远场.文献[10]提出了一种在近场超级透镜基础上发展出来的远场超级透镜(far- field superlens,FSL),它可以将放大后的凋落波通过紧邻的耦合元件转换成传播波,传播到远场参与成像,获得亚波长远场像.然而,该透镜局限性体现在:首先,物体必须在FSL的近场范围内,在凋落波衰减之前将其放大并耦合成传播波;其次,耦合元件的光学传递函数需要严格设计,确保凋落波信息准确重建参与成像.此外,传播波的频率范围有限,只能让一部分凋落波分量转化成传播波,因此该远场成像透镜的超分辨率能力也很有限.另一种方法是基于Pendry圆柱透镜理论提出的双曲透镜(hyperlens)[11,12],通过坐标变化将各向异性平板透镜的色散曲线变换到圆柱坐标系下,在各向异性介质中则形成双曲线色散关系,根据角动量守恒原理横波分量被不断压缩,凋落波被转化为传播波到达远场,可实现理想的远场超分辨率成像.然而,这些光学领域的特殊材料限制了其在微波领域的应用.在微波频段,Fink团队提出了由亚波长周期阵列构成的谐振超透镜,该周期结构可将凋落波转换为传播波,并将目标的空间信息包含在频谱分量中,用于超分辨率图像的重构[13,14],类似的还有利用磁耦合作用的磁透镜[15−17].此类结构的局限性在于工作频带较窄,在宽带领域应用受限.宽带成像系统具有功耗低、分辨率高和复杂性低等优点,在实际应用中具有诸多优势.在宽带超分辨率成像领域,文献[18]通过不同尺寸线谐振器的组合,设计了一种具有较宽工作频率范围的一维平面超透镜(planar-metalens,P-ML),对点源实现了超分辨率聚焦与成像,但是一维结构会受限于实际应用.文献[19]则利用非谐振超材料设计了一种圆柱坐标系下的宽带椭圆透镜,类似于双曲透镜,该透镜可在较宽的频带范围实现椭圆空间色散关系,将凋落波转换为传播波,从而实现超分辨率成像,缺点是需要通过扫描方式进行图像重构.

基于立体超材料概念,本文提出了一种具有较宽工作频带的透镜用于实现二维目标远场超分辨率成像,这里称之为立体超透镜(stereo-metalens,S-ML).该S-ML结构单元具有两个谐振频率,且这两个谐振频率具有一定的间隔,周期排列时体现出宽频带特性.由于阵列中存在的Bloch模式可将目标凋落波转换为传播波,使目标的亚波长细节信息传播到远场,因此远场接收的信号可重构出目标图像.本文分别从频域和时域对借助S-ML的目标进行了超分辨率特性验证,仿真结果证明可借助所提出的S-ML实现目标远场超分辨率成像,并且结合时间反演技术,验证了带宽提升对空间超分辨率聚焦特性带来的优势.

2 原理及结构设计

在化学学科中,立体化学的一个重要组成部分就是同分异构体,即具有相同化学式但原子空间排布不同的物质,且原子相对位置对化学物质的性质具有很大的影响.类似于化学中的同分异构体,纳米光子学中的立体超材料指的是具有相同组成单元但却有不同空间分布的超材料[20].基于这种概念,本文提出了一种立体超材料透镜,该透镜由两个方螺旋谐振器构成,两个谐振器呈上下摆放,通过调整相互之间的旋转角度达到不同组合的效果.此时,每种组合都存在两个谐振频点(ω−和ω+),这种现象称之为等离子体的混合作用,是由两个单元的相互靠近引起的[21−23].谐振器单元印制在一块相对介电常数为2.65、厚度为1 mm的介质板的两侧,如图1所示.金属条带的宽度和相邻条带之间的间距均为0.5 mm,沿x方向最外面的条带长度为8.5 mm,沿y方向最外面条带的长度为8 mm,工作频率为1.33 GHz.

为了研究这个模型的谐振频率随角度的变化,利用CST Microwave Studio中的本征求解器(Eigenmode Solver)进行分析.在保持上层单元不变的情况下,以下层单元对上层单元的旋转角度θ为变量,如图1(b),令θ从0◦到180◦变化,通过本征模求解可得到相应的本征频率.图1(c)给出了求解得到的两个本征频率与旋转角度θ之间的关系,可以看到,每种组合都会产生两个谐振,且两个谐振之间有一定的频率间隔.我们知道,当亚波长谐振器进行周期排列时,相互之间的耦合作用会使阵列在谐振频率附近产生很多分裂的谐振频点.基于这个原理,将所提出的立体超材料模型拓展为20×20的阵列,选择θ为90◦时的情形形成S-ML进行验证.这里选择θ为90◦主要是进行原理性的验证,其他旋转角度也是可行的.为了验证S-ML的近远场模式转换效果,选择一个臂长为1 mm的小偶极子作为一个点源放置在透镜上方2 mm处来激励该透镜,并在透镜的近场和远场区记录接收到的频谱信息.同时,选择与S-ML对应的P-ML作为对比,其为仅由单层金属条带(图1中的黑色部分)和介质板构成的周期阵列结构.将得到的频谱幅度以最大值做归一化处理,图2中黑色实线显示的是有S-ML时仿真记录到的近远场频谱,在1.06—1.53 GHz范围内发生了明显的谐振,而P-ML仅在1.2—1.4 GHz工作,如图3所示,可见S-ML可大幅提升工作频带.另外,图2中红色虚线表示的则是无S-ML时记录的近远场频谱,将其幅度以有S-ML时的近远场频谱峰值幅度做归一化处理,如图2中右边刻度所示,可以发现并没有谐振的产生,且幅度也远远小于有S-ML时的幅度,从而验证了S-ML可将目标凋落波转换为传播波并辐射到远场的能力,这为远场超分辨率成像奠定了基础.S-ML实现远场超分辨率成像的机理是基于文献[12]提出的谐振超透镜.利用周期排列的亚波长谐振器阵列,成像目标激励起的凋落波和传播波都将被转换为阵列结构中的Bloch模式,该模式同时携带着目标的亚波长细节信息和大空间尺寸信息,其为传播波模式,因此可以通过阵列的谐振特性辐射到远场.色散关系的存在则将这些Bloch模式携带的空间信息与频率联系起来,通过放置在远场的天线接收频谱信息进而实现远场超分辨率成像.

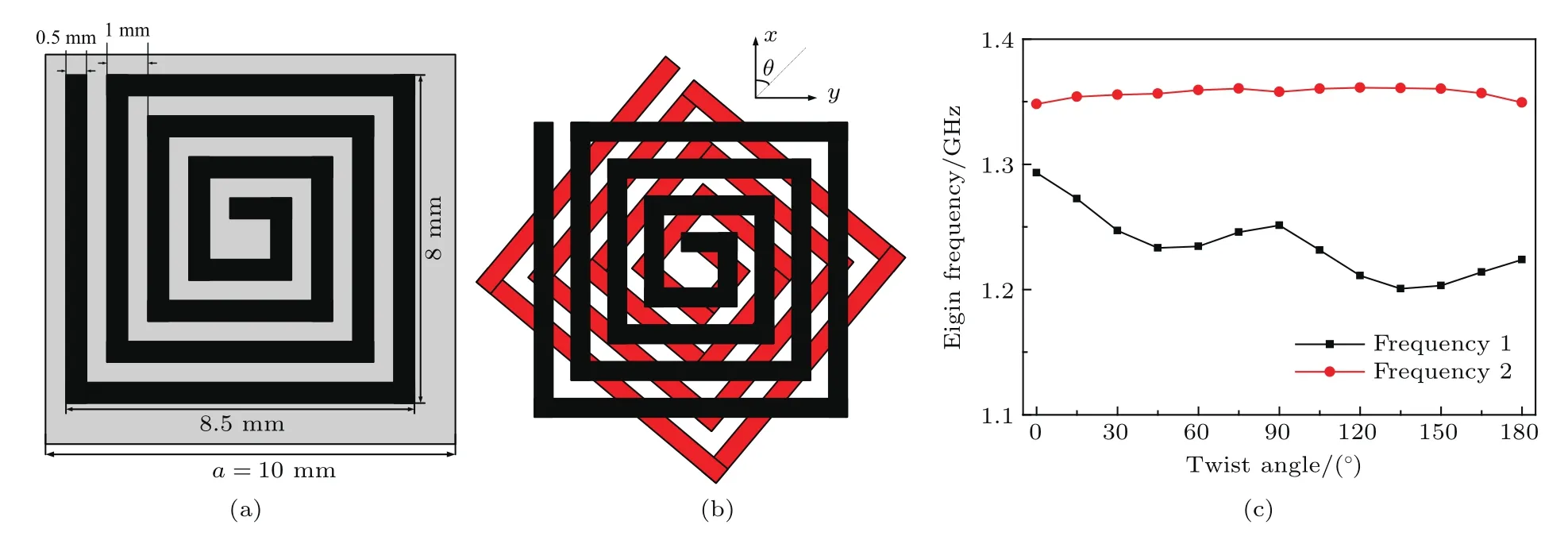
图1 S-ML的单元物理尺寸、几何模型以及本征频率与旋转角度之间的关系 (a)物理尺寸;(b)几何模型;(c)本征频率与旋转角度之间的关系Fig.1.Physical dimensions and geometric model of the S-ML:(a)Physical dimensions;(b)geometric model;(c)the relationship between eigen frequency and twist angle.

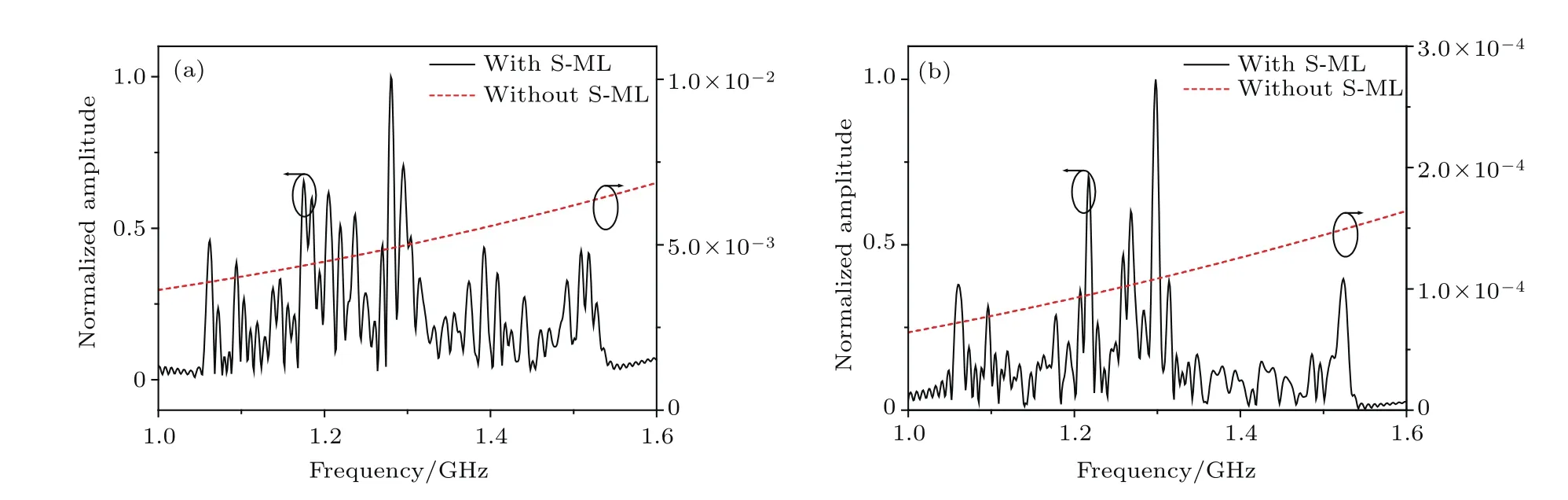
图2 有无S-ML时的近远场频谱 (a)近场区域;(b)远场区域Fig.2.Numerical simulation results of frequency spectra with and without the S-ML:(a)Near- field;(b)far- field.

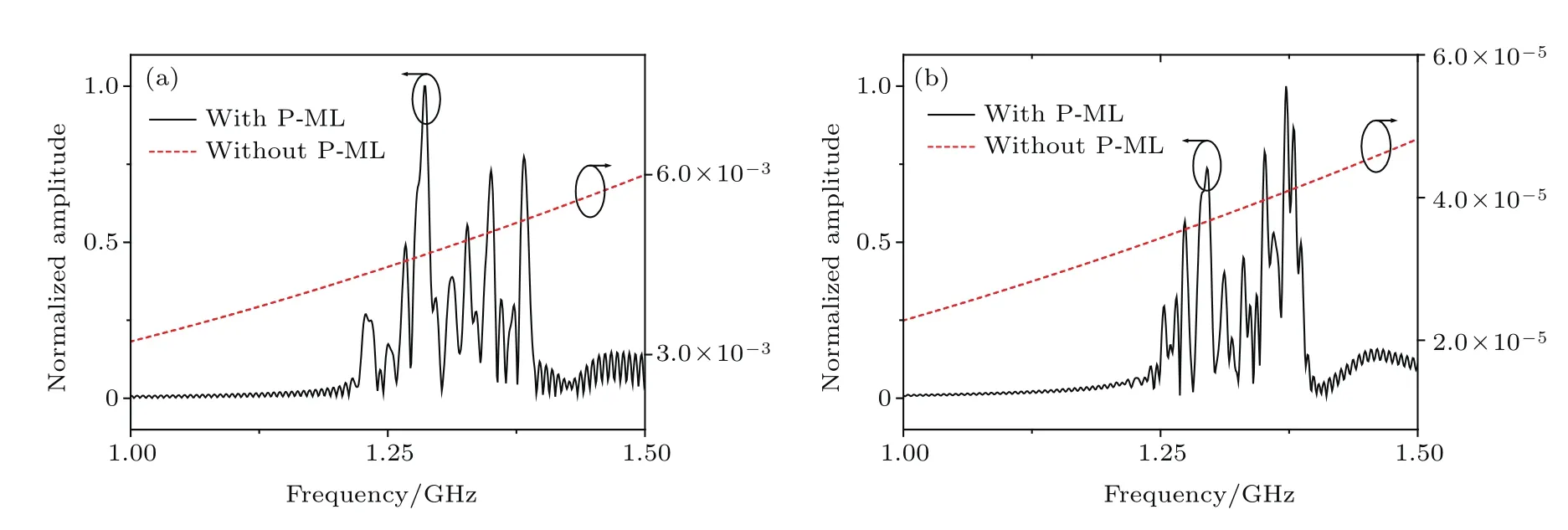
图3 有无P-ML时的近远场频谱 (a)近场区域;(b)远场区域Fig.3.Numerical simulation results of frequency spectra with and without the P-ML:(a)Near- field;(b)far- field.

3 远场超分辨率特性验证与分析

针对所提出的S-ML,利用该透镜进行拓展目标的超分辨率成像,模型如图4所示.成像目标为两根半径5 mm、长度为70 mm的金属圆柱,两根圆柱放置在透镜上方10 mm处.这里采用14个工作频率为1.3 GHz的偶极子天线作为收发天线,天线放置在距离透镜5λ处,λ为自由空间中的工作波长,采用三维全波仿真软件CST Microwave Studio进行成像仿真,仿真频率范围设为0.8—1.6 GHz.成像步骤如下:

步骤1在仅存在S-ML时,在成像目标所在平面设置频域电场监视器记录该平面上的电场E(幅度和相位),每隔0.1 GHz取一个频率采样点.当每个天线依次作为发射天线时,该平面上记录的场可视为天线与该平面之间的格林函数G,此时其他天线都作为接收天线,由此会得到一个14×14的散射矩阵,该矩阵表示天线间的频域响应关系,记为KS;

步骤2在透镜和成像目标同时存在时,重复步骤1的操作,得到另一个14×14的散射矩阵,记为KO;

步骤3计算散射矩阵K=KS−KO,其包含着成像目标的空间信息;

步骤4利用散射矩阵K和格林函数G通过多重信号分类算法进行成像[24,25].

图5(a)为1.3 GHz时的二维成像结果,取沿x=0轴上的数据可得到图5(b)的能量密度分布.若以半峰宽度作为分辨率的定义标准,其为19 mm,相当于λ/12,远远小于瑞利判据的极限,实现了远场超分辨率成像.作为对比,还进行了无S-ML存在时的成像,步骤同上,结果如图6所示,此时分辨率大于340 mm,相当于1.5λ,远小于S-ML存在时的结果,证明借助S-ML可显著提高目标成像分辨率.

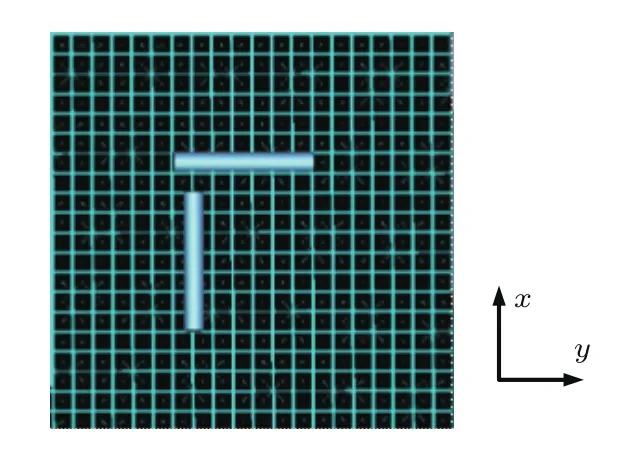
图4 拓展目标超分辨率成像模型Fig.4.Super-resolution imaging model of extended target.

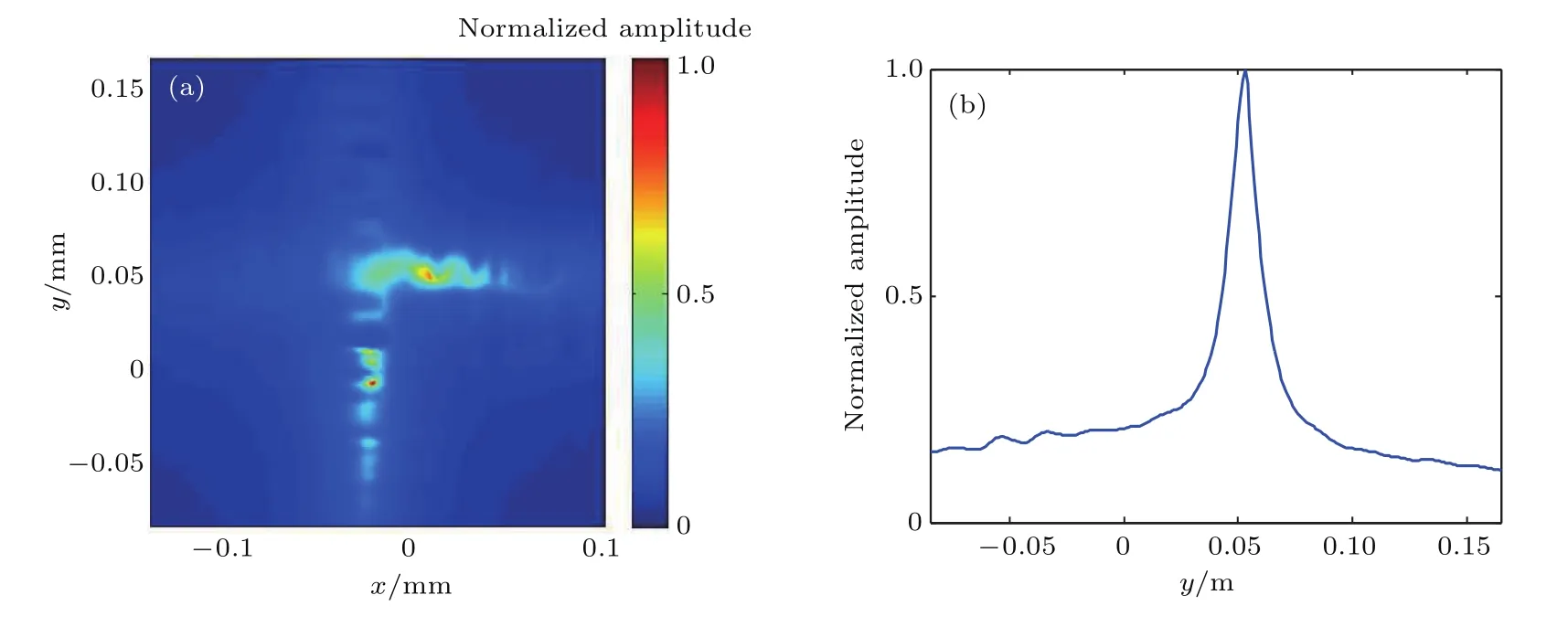
图5 利用S-ML的二维成像结果 (a)二维成像结果;(b)沿线x=0的能量密度分布Fig.5.Imaging result with the S-ML:(a)Two-dimensional imaging result;(b)intensity distribution along the line of x=0.

利用时间反演技术从时域上来验证带宽提升带来的空-时聚焦优势[26,27].仿真模型如图7所示,3个点状的小偶极子(A1,A2和A3)作为聚焦目标,位于透镜上面2 mm处,间距为9 mm,相当于λ/24,8个工作在1.3 GHz的半波偶极子天线(D1—D8)放置在离透镜10λ处作为时间反演镜在远场的接收信号.

仿真步骤如下:

步骤1选择A2作为聚焦目标来发射激励信号x(t);

步骤28个半波偶极子天线(D1—D8)接收信号,记为yn,2(t)(n=1,2,···,8);

步骤3将信号yn,2(t)(n=1,2,···,8)利用计算机在时域上进行反转得到时间反演信号yn,2(−t)(n=1,2,···,8);

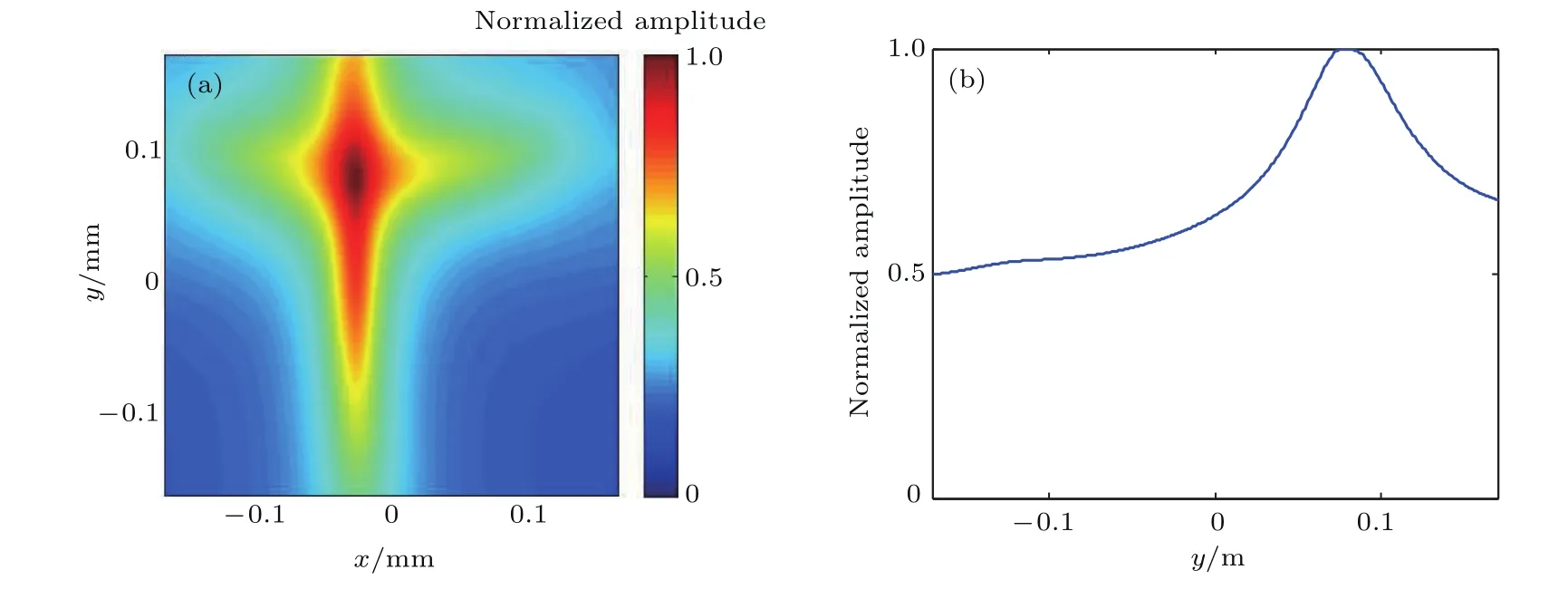
图6 无S-ML的二维成像结果 (a)二维成像结果;(b)沿线x=0的能量密度分布Fig.6.Imaging result without the S-ML:(a)Two-dimensional imaging result;(b)intensity distribution along the line of x=0.

步骤4将信号yn,2(−t)(n=1,2,···,8)再通过D1—D8重新发射,此时A1—A3会接收到时间反演聚焦信号

聚焦信号结果如图8所示,可以看出作为目标天线的A2接收到的聚焦信号峰值幅度远大于A1和A3的聚焦信号峰值幅度,将A1—A3聚焦信号的峰值幅度做归一化处理,如图8中黑色方块标识所示.可以看出,在S-ML的帮助下,能够明显分辨间距为λ/24的目标.作为对比,对P-ML情形进行同样的时间反演聚焦仿真,如图9中红色圆形标识所示,可以看出黑色方块曲线比红色圆形曲线具有更好的区分度,即聚焦效果具有更好的区分度,说明更宽工作频带的S-ML可展示出更好的空间超分辨率特性.相对于文献[18]中的一维结构和文献[19]中的扫描成像方式,所提出的S-ML具有良好的二维超分辨率特性,因此该成像方法更具有实际应用价值.

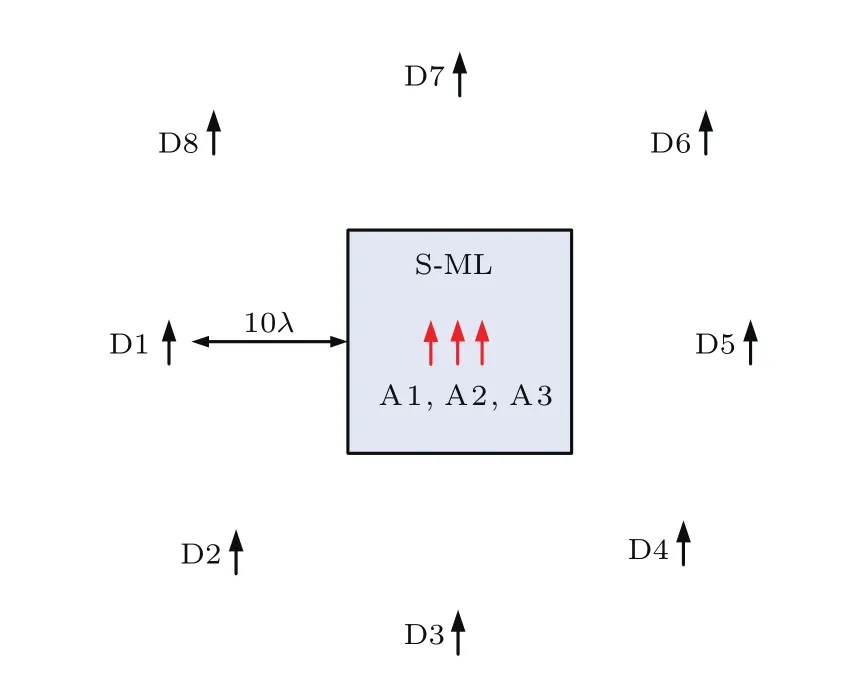
图7 时间反演仿真模型示意图Fig.7.Time reversal simulation model diagram.

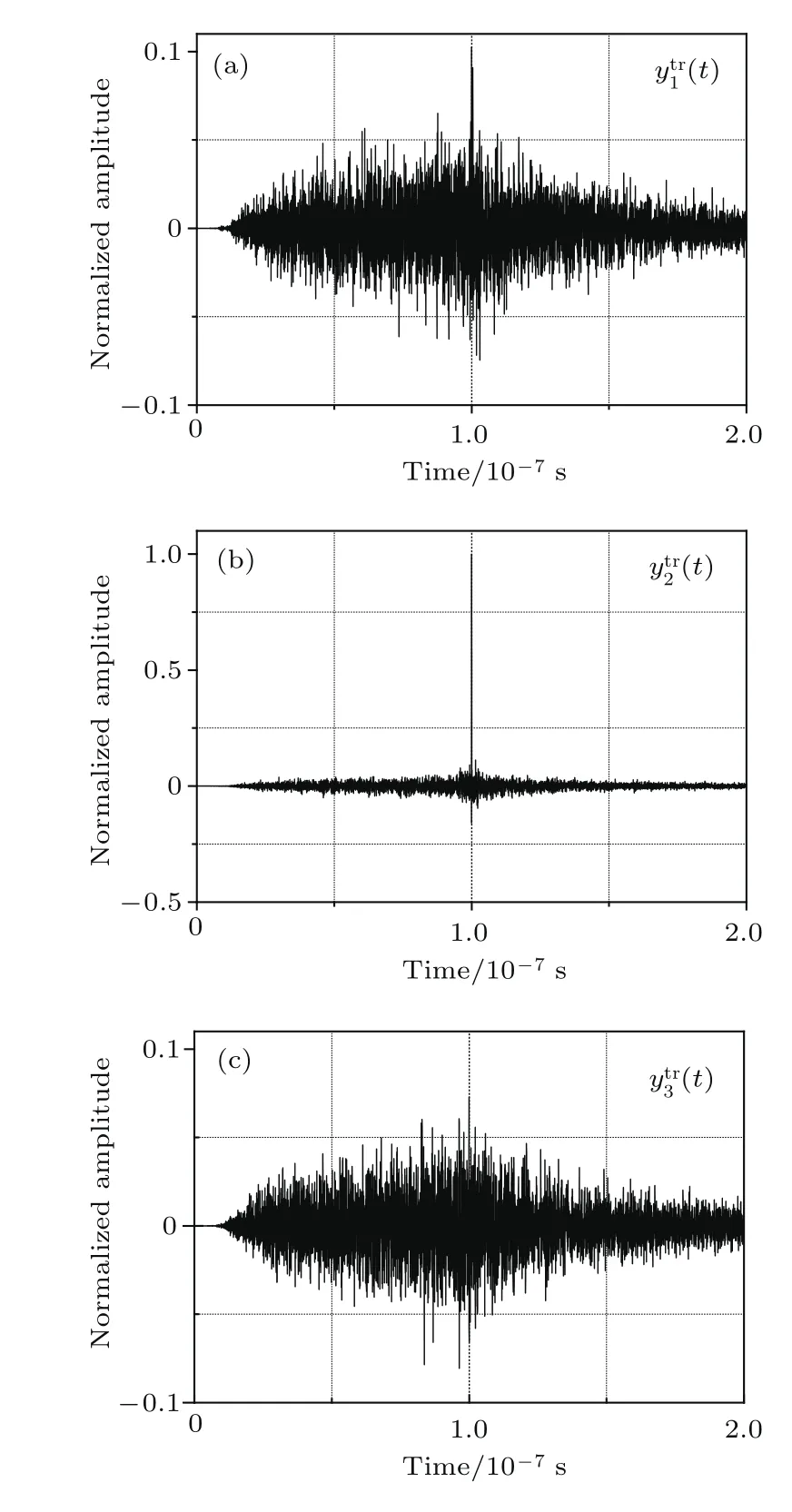
图8 时间反演聚焦信号(a)A1接收到的聚焦信号(b)A2接收到的聚焦信号(c)A3接收到的聚焦信号Fig.8.Time reversal focusing signals:(a)Focusing signalreceived by A1;(b)focusing signalreceived by A2;(c)focusing signalreceived by A3.

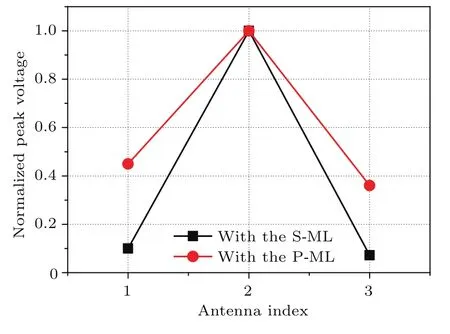
图9 时间反演空间超分辨率聚焦特性Fig.9.Spatial super-resolution characteristic of time reversal focusing.

4 结 论

本文提出了一种宽带S-ML用于实现目标的远场超分辨率成像.基于立体超材料的概念,设计了具有一定频率间隔单元模型,利用该单元模型组成了具有宽带特性的S-ML.近远场频谱的对比验证了该透镜可将凋落波转换为传播波,从而可应用于远场超分辨率成像.相对于P-ML,本文提出的S-ML具有更宽的工作频率范围.从频域和时域两方面验证了该透镜的超分辨率成像能力,对提升传统成像系统的性能具有重要价值.

参考文献

[1]Merlin R 2007Science317 927

[2]Grbic A,Jiang L,Merlin R 2008Science320 511

[3]Grbic A,Merlin R 2008IEEE Trans.Antennas Propag.56 3159

[4]Zhu S X 2000Opt.Instrum.22 34(in Chinese)[祝生祥2000光学仪器22 34]

[5]Pohl D W,Denk W,Lanz M 1984Appl.Phys.Lett.44 651

[6]Pendry J B 2000Phys.Rev.Lett.85 3966

[7]Pendry J B,Ramakrishna S A 2003J.Phys.:Condens.Matter15 6345

[8]Nicholas F,Lee H,Sun C,Zhang X 2005Science308 534

[9]Yang C,Zhang H X,Wang H X,Xu N,Xu Y Y,Huang L Y,Zhang K X 2012Acta Phys.Sin.61 164101(in Chinese)[杨晨,张洪欣,王海侠,徐楠,许媛媛,黄丽玉,张可欣2012物理学报61 164101]

[10]Liu Z W,Durant S,Lee H,Pikus Y,Fang N,Xiong Y,Sun C,Zhang X 2007Nano Lett.7 403

[11]Liu Z W,Lee H,Xiong Y 2007Science315 1686

[12]Lü C,Li W,Jiang X Y,Cao J C 2014Europhys.Lett.105 28003

[13]Lemoult F,Lerosey G,de Rosny J,Fink M 2010Phys.Rev.Lett.104 203901

[14]Lemoult F,Fink M,Lerosey G 2011Waves Random and Complex Media21 614

[15]Ourir A,Lerosey G,Lemoult F,Fink M,de Rosny J 2012Appl.Phys.Lett.101 111102

[16]Jouvaud C,Ourir A,de Rosny J 2014Appl.Phys.Lett.104 243507

[17]Wang R,Wang B Z,Gong Z S,Ding X 2015Sci.Rep.5 11131

[18]Gao Q,Wang B Z,Wang X H 2015IEEE Trans.Antennas Propag.63 5586

[19]Zheng B,Zhang R R,Zhou M,Zhang W B,Lin S S,Ni Z H,Wang H P,Yu F X,Chen H S 2014Appl.Phys.Lett.104 073502

[20]Liu N,Liu H,Zhu S,Giessen H 2009Nat.Photon.3 157

[21]Prodan E,Radlo ffC,Halas N J,Nordlander P 2003Science302 419

[22]Wang H,Brandl D W,Le F,Nordlander P,Halas N J 2006Nano Lett.6 827

[23]Nordlander P,Oubre C,Prodan E,Li K,Stockman M I 2004Nano Lett.4 899

[24]Cheney M 2001Inverse Prob.17 591

[25]Gruber F K,Marengo E A,Devaney A J 2004J.Acoust.Soc.Am.115 3042

[26]Fink M 1992IEEE Trans.Ultrason.Ferroeletr.Freq.Control39 555

[27]Lerosey G,de Rosny J,Tourin A,Derode A,Montaldo G,Fink M 2004Phys.Rev.Lett.92 193904