坐标空间中构造的Breit夸克势与介子和夸克偶素的质量劈裂∗

吉日木图 敖登 薛康

(内蒙古医科大学计算机信息学院,呼和浩特 010110)

1 引 言

夸克间的相互作用是复杂的,表示这种相互作用的理论模型也比较多见[1−5],到底何种模型能够准确无误地表达这种相互作用,至今尚未定论.这其中比较流行且常用的是非相对论夸克势模型,如常见的Breit势函数[1,2,6−8].这种夸克势模型认为强子内夸克的运动是非相对论的,因此它(夸克的运动)可以用薛定谔方程很好地描述.虽然这种模型对轻夸克的描述不尽合理,但它对强子束缚态和散射方面的计算都取得了较大的成功[1,6−17],因此人们一直用非相对论性夸克势模型来描述包括轻夸克在内的夸克之间的相互作用[5,10,16−21],并且与其他方法相比,这种模型在束缚态的计算方面显现得更加优越[22].这些实事和成功促使人们对它进行更为广泛和深入的研究,使之变得更加完善精确,从而构造出新的势函数[10,16−21].

由于在微观的强相互作用中,势函数的厄米性和非定域性(含两变量坐标和动量)是一个不可忽视的重要特征.因此构造新势函数不能简单随意删改现有势函数中的某几项[10−15,18]来实现,不恰当的删改就会破坏势函数应有的完整性、厄米性和非定域性.

众所周知Breit势中包含r−3的奇异项[2,20],要构造一个有效稳定的势函数,其出发点应该是要消除Breit势的奇异性.文献[10,15,17—19]直接在坐标空间中通过简单的删改或替代方法不同程度地消除Breit势中的奇异因子来实现构造势函数.

在微观领域中原子尺寸范围内极小程度地提高精度都很艰难.文献[19]中,ηc的实验质量和理论质量分别是2.979和3.025 GeV,J/ψ的实验质量和理论质量分别是3.097和3.052 GeV,相应的屏蔽质量µ值为0.894 GeV,这也是π-ρ劈裂时的µ值.在宏观领域,此种情况可认为理论和实验值严格相等,但在微观领域,想缩小这微小的差距并非易事.首先保证构造势有效,然后是合理有效地构造屏蔽质量µ的解析式.若构造势有效,但数值计算技能不恰当的情况下,也就无法证明构造势有效.因此每一环节都非常重要且艰难,且缺一不可.对于文献[19],经过一系列的计算发现,几个重要夸克偶素ηc,J/ψ,χc0,χc1,χc2之间无法质量劈裂.由此断定文献[19]构造的势函数(16)式的有效度并不高.

在先前研究基础上如何重新组合、怎样有效合理搭配各项,是构造有效势函数的关键,也是难点,还需保证势函数的整体形式从前没有出现过.文献[19]中(16)式不能计算劈裂除了(16)式的各项选取和搭配并非合理外,还有一个原因是文献[19]中(3)式的自旋-自旋耦合项(σi·σj)的系数是2/3(势函数直接取自文献[2]),而在本文中这个系数是3/3(势函数是从动量空间得到),这个系数的不同对计算劈裂影响较大.

鉴于上述,本文是在文献[19]的基础上重新合理选取并有效搭配各项而构造形成势函数.通过一系列的分析讨论可知,并非每一种构造方法都可以得到有效势函数.

本文对完整的坐标空间中的Breit势的各项进行逐项替代处理,这样重新得到的势函数在坐标空间中不再含r−3的奇异项.计算结果表明,用本文的替代方案可以消除Breit势的奇异性,得到比以往更加稳定和高精度的介子质量谱,从而构造出一个有效的夸克势模型(函数).

2 坐标空间中的Breit势

用傅里叶变换把动量空间中的Breit势函数[1,6−8,20,21]变换到坐标空间中,得到的势函数与直接在坐标空间中给出的Breit势函数[2]有所出入,所以我们对Breit势的改进还是从动量空间开始.把动量空间中的Breit势函数稍加整理(合并同类项)得到

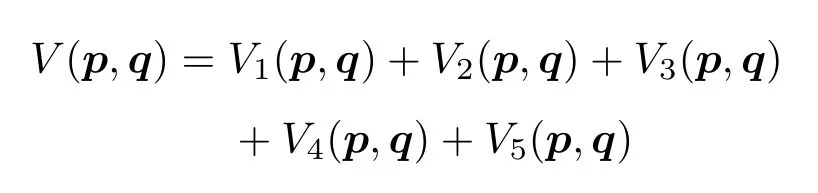
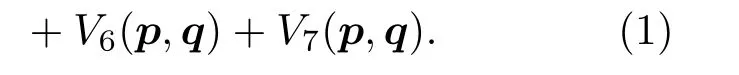
(1)式中各项的具体表达式如下:

其中,是散射道色矩阵[10];αs是量子色动力学耦合常数;mi和mj是夸克i和夸克j的组分质量;σi是夸克i的Pauli矩阵;最后一项V7(p,q)是常数项势,用以求解薛定谔方程时调整介子质量而增加的项[10,20];p和q的意义与文献[20]相同.

然后用傅里叶变换公式

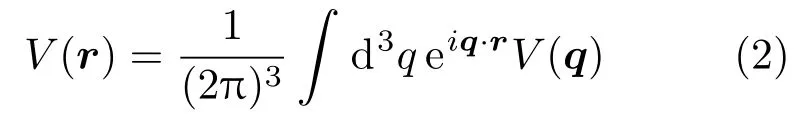
把势函数(1)的每一项变换到坐标空间中,再加到一起,就得到坐标空间中的Breit势函数:

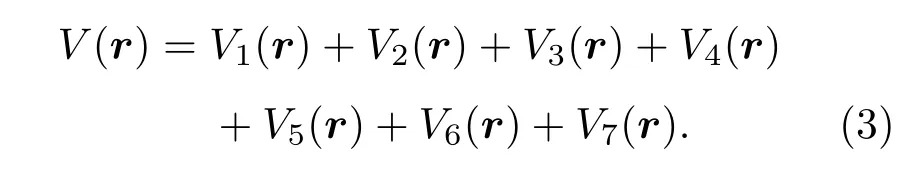
(3)式中各项的具体表达式如下:

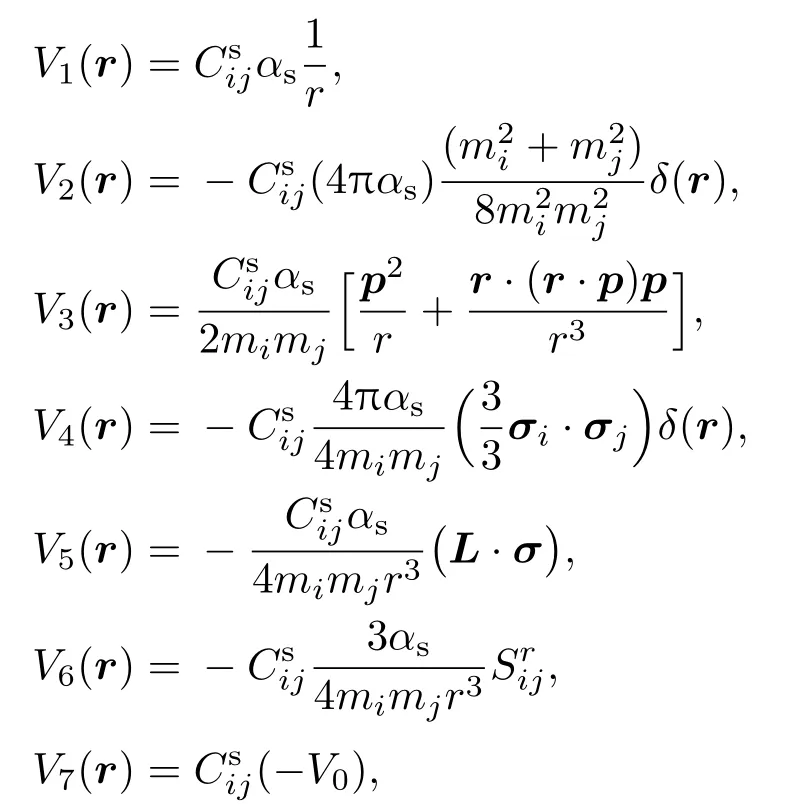
其中,L=r×p是介子轨道角动量算符,是张量力算符.

3 在坐标空间中构造新的Breit势

根据文献[23],在坐标空间中势函数的某一项关于r的渐近行为如果是r−3,那么该项就是奇异项.由文献[20]可知,δ(r)函数及动量p的渐近行为是δ(r)∼r−3和p∼r−1.由此势函数(3)式各项的渐近行为如下:V1(r)∼r−1,V2(r)∼r−3,V3(r)∼r−3,V4(r)∼r−3,V5(r)∼r−3,V6(r)∼r−3,所以V2(r)至V6(r)项都是奇异项,需要修改重新构造.

为了兼顾计算精度和稳定度,并结合文献[19]的方法,除了势函数(3)式的第一项库仑势V1(r)和第七项常数项势V7(r)外,对其他的各项都得进行如下的不同的逐项替代.把Vi(r)(i=2,3,4,5,6)进行替代后得到的项记作则新构造的势函数各项的具体表达式如下:

由于V2(r)∼δ(r),该式表示介子内两夸克只有当距离很近(r→0)时才有作用,并且无限大(绝对值),否则就无作用.这显然不符合物理量随距离的增大而逐渐衰减的普遍原理,需要修改.已知

并结合文献[5,10,17,19]的方法及数值计算精度,把势函数(3)式中的δ(r)函数用如下的变换来替代:

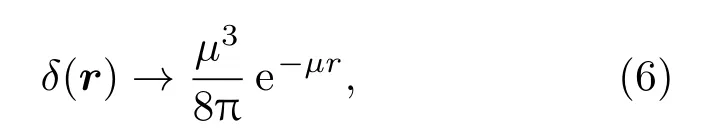
得到坐标空间中新的V2(r),

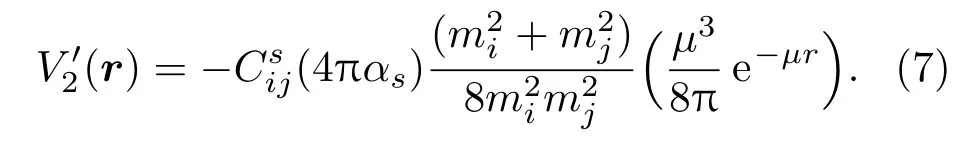
由(7)式可直接看出r=0已不再是奇异点,从而消除了奇异.第(7)式中出现的参量µ是可调参量,也称屏蔽质量.根据文献[20,21,24],µ并非一个简单的常数,而应该是与夸克质量mi,mj有关,这将在后面详细讨论.

由(7)式可知,当屏蔽质量µ>0时随距离的增大而逐渐衰减,最后变成零.r=0时作用最大µ3/(8π)(绝对值),并且屏蔽质量µ越大此作用越大.同理,在后面讨论的V4(r)的替代与V2(r)相同,相关的讨论结果也相同.

把势函数(3)式中的第三项稍加改写为

(对重复脚标k求和),很容易看到,如果能消除因子1/r的奇异性,那么第三项V3(r)为非奇异项.

势函数(3)的第三项V3(r)有奇异点,当r=0时发散.所以修改的出发点应该是当r=0时使之收敛.有如下的渐近行为:

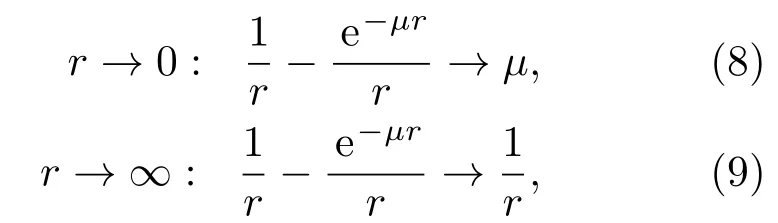
因此做如下替代:

这样无论r→0还是r→∞,变换(10)式能消除奇异点.考虑到势函数的厄米性,把势函数(3)式的第三项V3(r)重新构造如下:

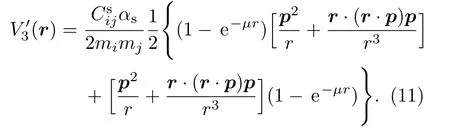
重新构造出的是非奇异项.

综上可知,当屏蔽质量µ=0时对任意的r直接有1/r→0,当屏蔽质量µ<0时1/r−e−µr/r直接发散,因此必须有µ>0,这已表明构造两种不同方法之下所引进的屏蔽质量µ(认为在各个环节中µ是同一的)的性质很自然地统一到一起,也在一定程度上证实了所构造的的正确性.

第四项V4(r)的改进方法同第二项V2(r)的改进方法,用到变换(6)式,得到

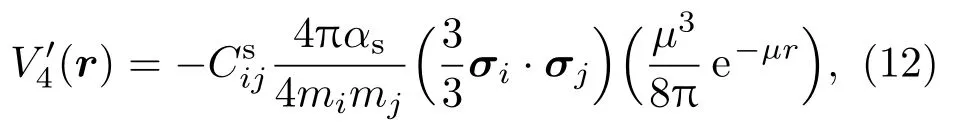
势函数(3)式的第五、六项V5(r),V6(r)也是奇异项.第五项V5(r)的改进方法要结合第三项V3(r)的改进方法.由(10)式得到如下替代公式:

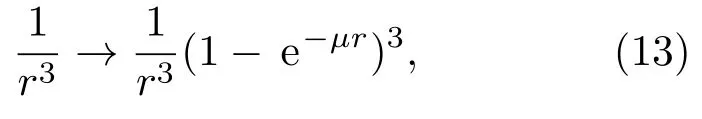
而有

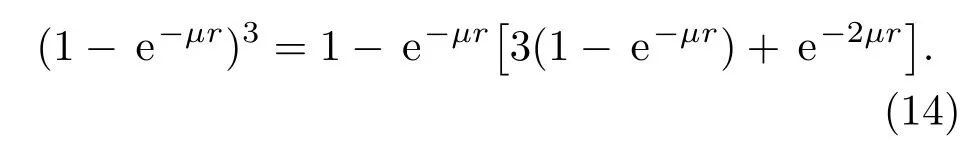
因为要求势函数只含e−µr的一次幂,所以把(14)式中的因子3(1−e−µr)+e−2µr进行级数展开,并忽略µr的二次幂及以上的高阶项,得到近似公式:

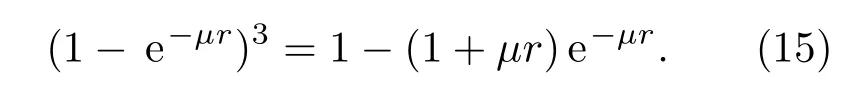
把(15)式代入(13)式,得到替代公式:

将V5(r)和V6(r)中的1/r3用(16)式替代,得到新的第五项和第六项,

由(17)和(18)式可知,V5(r)与V6(r)变换前后关于r的空间部分相同的性质不变,因此(17),(18)式是合理的.

下面分析(17)或(18)式是否消除了奇异.因为其中已代入e−µr的级数展开式,由此可知表明或是非奇异项.

把(4),(7),(11),(12),(17),(18)式进行相加,得到一个重新组合的非奇异的、有效的夸克势模型在坐标空间中的形式:

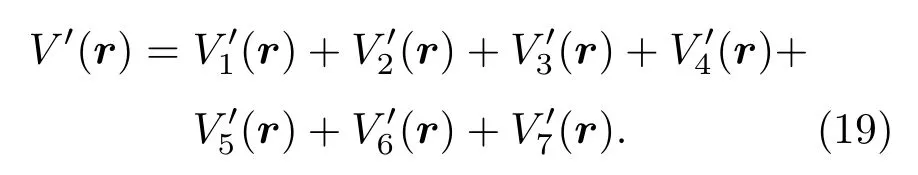
禁闭势采用文献[10,20]线性禁闭势,

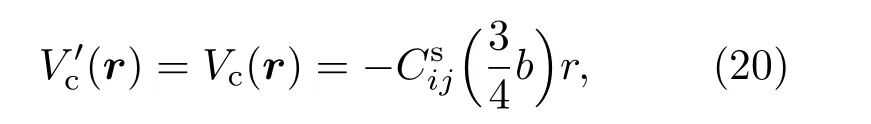
将(19)和(20)式相加得到总势函数

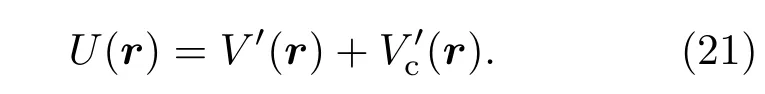
4 新构造势的矩阵元

计算矩阵元时直接采用文献[21]给出的一般公式第(26)和(27)式,并只给出l=0,1和l′=l时的矩阵元,其中出现的参量wn,Al的定义与文献[21]中的第(31)和(33)式相同,可通过计算得到势函数(19)式的各项矩阵元,其中第一项库仑势矩阵元第七项常数项势矩阵元和禁闭势矩阵元分别由文献[21]中的第(34),(40)和(41)式给出,在这里不一一列出.

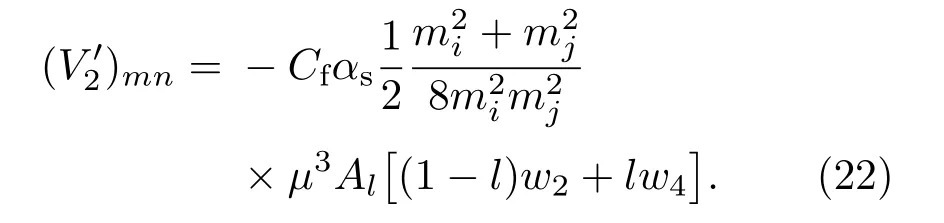
第三项是轨道-轨道耦合项:

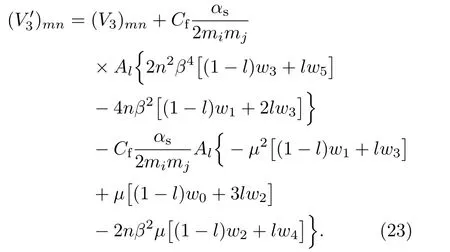
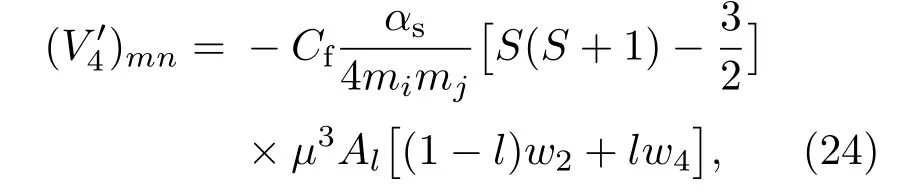
第五项是自旋-轨道耦合项:

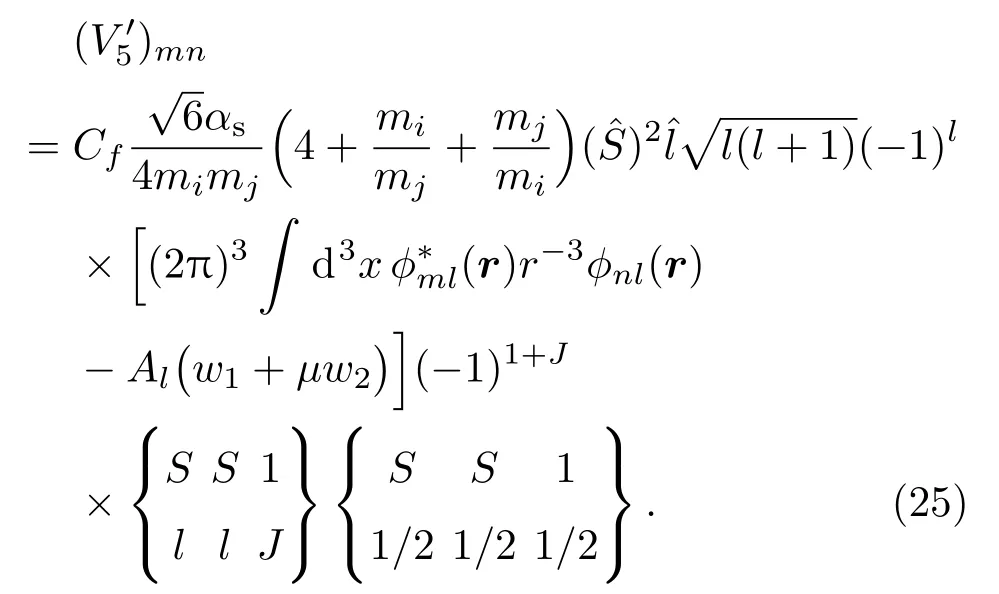
第六项是张量力项:

(23)式中出现的矩阵元(V3)mn,(25)和(26)式中出现的空间积分分别由文献[21]中的第(42)和(44)式给出,在这里不一一列出.至此把势函数(19)的每一项矩阵元一一计算完毕.

5 屏蔽质量µ与夸克质量mi,mj有关

屏蔽质量µ到底与哪些量有关,可从势函数(19)或(21)式所含的可调参量出发研究,包括弦张力系数b,常数项势V0,五种夸克质量mu(mu=md),ms,mc,mb以及屏蔽质量µ.如果问题中µ并非常数(也可以是各个介子µ值相同的常数),是变量(各个介子µ值不同)的话,它不可能与b,V0有关,因为b,V0并非势函数常含量,所以只能说µ应该与夸克质量mi,mj有关,这是最早的思路[20,24].

夸克质量有两个mi,mj,即两个变量,此时µ是关于mi,mj的二元函数,此时使用极不方便.因此可将mi,mj先进行简单组合构造一个新自变量,然后用这个新自变量再表达µ,可实现µ是一元函数的构想,这些都是当时的思路.

组合这个新自变量时需满足如下要求:新变量对mi,mj的交换是对称的.常用的新自变量有折合质量µr=mimj/(mi+mj),平均质量µa=(mi+mj)/2,应该还有其他形式的新自变量,这里不予以给出.

文献[5,24]中取µ与折合质量µr成正比的特简单的形式,即µ=cµr.如果计算数目庞大的一组介子质量,那么此关系式应该远不是这么简单的形式,并且自变量不一定是µr.所以文献[5,24]中提到的势函数所附带的屏蔽质量µ的正确形式是另外一种,只有计算数目庞大的一组介子质量时才能找到,仅凭物理意义很难找到关系式.

本课题组相关工作[20,21]中都取µ是折合质量µr的函数,并且形式远不是成正比这么简单,是通过计算来确定的.不同的势函数所需要的µ不同,不但函数形式不同,而且有可能自变量也不同.对于本文计算,首选自变量为折合质量µr,但无论怎么计算,数值计算精度都很差,因此改用平均质量µa作为自变量构造屏蔽质量µ,计算精度比以往更高,相关数据列于表1.

构造屏蔽质量µ的有效表达式是比构造势函数还要艰难且难度极大的问题,根据以往的推导和数值计算,对于一般的势函数,不可能简单地成正比关系.除了势函数有效和特定的µ值外,还需要较高的数学技能和数值计算能力,这也是个新问题.

需要说明的是,构造屏蔽质量µ的有效表达式时注重数学技能和数值计算,兼顾物理意义.如果单凭物理意义只会找到成正比这样简单的关系,无法找到复杂的关系式.

6 构造屏蔽质量µ的解析式

求解文献[21]给出的薛定谔方程(29)式之前还需构造(19)式中的屏蔽质量µ的表达式.根据以往的分析计算[20,21],当µ值小时,ηc-J/ψ等重介子不劈裂,而当µ值大时π-ρ(与重介子一起计算,计算结果未列入表1中,下同)等一系列轻介子都发散.因此要想使π-ρ,ηc-J/ψ和ηb-Υ(1s)等重要介子之间质量劈裂,屏蔽质量µ并非一个简单的常数,而应该是与夸克质量mi,mj有关的变量,势函数(19)式也不例外.

由上面的分析讨论,不同的势函数所需要的µ不同[20,21,24],对于(19)式构造µ是比构造势函数还要艰难且难度极大的问题.再好的势函数如果未能找到一个合适的µ与之相互匹配,从而就不能算出更高精度的质量谱,那么也就无法证实该势函数的有效性.因此能否找到一个合理、有效的µ的解析式为关键所在,它直接关系到一个势函数的有效性.

对于Breit势函数,介子之间要质量劈裂或要达到更高精度的质量时,各个介子所需的µ值不同,结构相同的介子µ值相同.其中π-ρ和ηc-J/ψ劈裂时其µ值为确定值,其他介子的µ值在一定范围内变化.

在µ为常数的情况下计算得到,π-ρ和ηc-J/ψ等精确劈裂时所需的µ值分别为0.932和3.677 GeV.除此之外,对于(19)式,几个D介子的µ值有一定的限制,在5.050 GeV左右波动.根据这几个特定值构造µ的表达式,并经过一系列大量的前期化简给出以夸克平均质量µa=(mi+mj)/2(mi,mj为同一个介子中的两个夸克质量)作为变量的µ的形式为

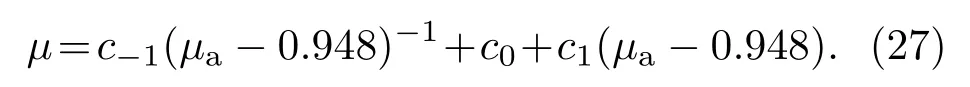
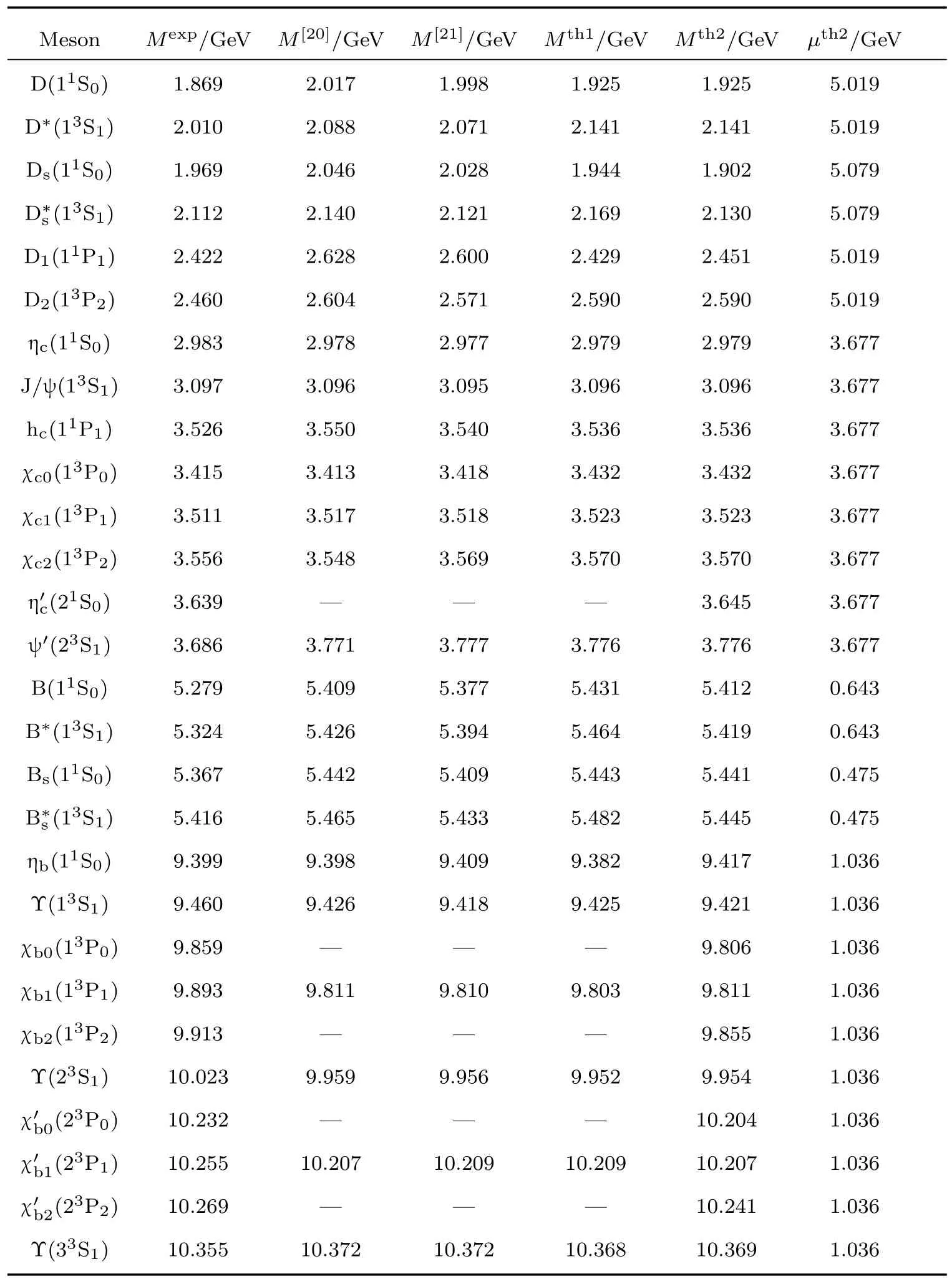
表1 本文计算结果与实验值的比较Table 1.Results of meson masses.

虽然由(27)式能够精确算出上述重要介子之间质量劈裂时所需的µ值,并且形式相对较简单,但不足的是用它无法控制几个B介子的µ值上涨到4.700 GeV左右,从而其质量精度不高,如表1所列.为了控制几个B介子的µ值,对(27)式推导步骤进行大量修正,其主要依据是几个B介子的µ值必须降低,同时保证维持其他介子现有的µ值.这样经过一系列的调整再仿照(27)式前期化简步骤进行化简之后得到

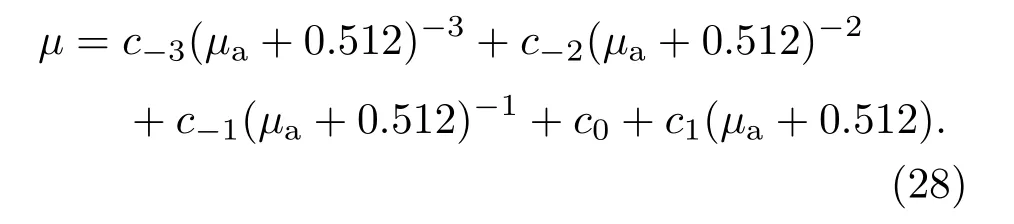
用(28)式计算得到几个B介子的µ值已经直接降到0.550 GeV左右,相应的质量精度也都有所提高,如表1所列.(27)式中的展开系数c−1,c0,c1和(28)式中的展开系数c−3,c−2,c−1,c0,c1是不同的,它们并非单一的可调参量,仅凭运算程序无法确定,一定要结合(27)和(28)式的前期化简过程和数值计算程序才能确定下来,并必须精确到小数点后五位,具体数值已列在表1的表注.

7 结 语

最后解文献[21]中给出的介子束缚态薛定谔方程(29)式Ha=EBa,通过运算程序先调节确定其中的可调参量弦张力系数b,常数项势V0,五种夸克质量mu(mu=md),ms,mc,mb的最佳值,然后分别用屏蔽质量µ的表达式(27),(28)式使π-ρ,ηc-J/ψ和ηb-Υ(1s)等重要介子之间进行质量劈裂,得到尽可能逼近实验值的介子质量数值解,从而检验势函数(19)式的有效性,同时调节出夸克质量等可调参量的更精确值.

直接计算验证,对于势函数(19)式,耦合常数αs和波函数中的宽度系数β仍采用文献[21]中使用的αs和β.

只计算少数介子或重介子或结构相同的夸克偶素[3,4]质量,远不足以证明势函数的有效性,因为此时各个参量的任意调节自由度很大,当然较容易实现劈裂或提高计算精度.因此要计算的一组数目较多的介子结构必须涉及五种夸克u,d,s,c,b,并含夸克偶素,此时的计算才真正考验新构造势(函数)的有效性.

为便于对比,表1列出了一些计算结果,其中,第1列数据Mexp是取自文献[10]的实验质量,第2列M[20]和第3列M[21]分别是文献[20,21]计算结果.第4列Mth1和第5列Mth2是本文在同一势函数(19)式情况下分别用(27)和(28)式计算的结果,第6列µth2是质量Mth2相应的µ值.从表1可容易看到,只有第5列Mth2的计算结果是更精确的,重要介子之间实现了精确劈裂,这恰是本文之精髓.

感谢内蒙古民族大学物理与电子信息学院特木尔巴根教授的有益探讨.

参考文献

[1]Barnes T,Black N 1999Phys.Rev.C60 045202

[2]Rújla A D,Georgi H,Glashow S L 1975Phys.Rev.D12 147

[3]Ebert D,Faustov R N 2000Phys.Rev.D62 034014

[4]Chen Y Q,Kuang Y P 1992Phys.Rev.D46 1165

[5]Zhou P,Deng C R,Ping J L 2015Chin.Phys.Lett.32 101201

[6]Chen J X,Su J C 2001Phys.Rev.C64 065201

[7]Wang H J,Yang H,Su J C 2003Phys.Rev.C68 055204

[8]Zhao G Q,Jing X G,Su J C 1998Phys.Rev.D58 117503

[9]Lucha W,Schoberl F F,Gromes D 1991Phys.Rep.200 127

[10]Wong C Y,Swanson E S,Barnes T 2001Phys.Rev.C65 014903

[11]Godfrey S,Kokoski R 1991Phys.Rev.D43 1679

[12]Godfrey S,Isgur N 1985Phys.Rev.D32 189

[13]Godfrey S 1985Phys.Rev.D31 2375

[14]Capstick S,Isgur N 1986Phys.Rev.D34 2809

[15]Wong C Y,Swanson E S,Barnes T 2000Phys.Rev.C62 045201

[16]Wang L,Ping J L 2007Chin.Phys.Lett.24 1195

[17]Zhang W N,Wong C Y 2003Phys.Rev.C68 035211

[18]Wong C Y 2004Phys.Rev.C69 055202

[19]Jirimutu,Wang H J,Zhang W N,Wong C Y 2009Int.J.Mod.Phys.E18 729

[20]Jirimutu,Zhang W N 2009Eur.Phys.J.A42 63

[21]Jirimutu,Aodeng,Bao tmurbagan 2016Acta Phys.Sin.65 041201(in Chinese)[吉日木图,敖登,包特木尔巴根2016物理学报65 041201]

[22]Crater H,Vanalstine P 2004Phys.Rev.D70 034026

[23]Landau L D,Lifshitz E M 1958Quantum Mechanics(London:Pergamon Press)

[24]Vijande J,Fernandez F,Valcarce A 2005J.Phys.G31 481