忆阻器、忆容器和忆感器的Simulink建模及其特性分析∗

王晓媛 俞军 王光义

(杭州电子科技大学,现代电路与智能信息研究所,杭州 310018)

1 引 言

1971年,Chua[1]根据电路的完备性提出了与电阻、电容和电感相并列的第四种电路元件——忆阻器;2008年12月,在伯克利大学举办的“忆阻器及忆阻系统专题报告会”上,Chua[2]再次指出,具有记忆特性的元件并不应该只局限于忆阻器,还应该推广至电容器和电感器.2009年,文献[3]中给出了对忆容器和忆感器两个元件的正式定义.同时指出,二者虽然也是记忆元件,但它们与忆阻器有着本质的不同,即它们是储能元件.三种记忆元件的符号如图1所示.

2008年5月,惠普(HP)实验室[4]首次成功地对忆阻器进行了物理实现,此举掀起了世界范围内对忆阻器研究的热潮.作为一种新型电路元件,忆阻器在非易失性存储[5]、人工神经网络[6,7]以及非线性电路[8,9]等多个领域表现出巨大的应用前景.但由于HP忆阻器受限于纳米工艺和严格的实验条件,目前尚不能走出实验室,而忆容器和忆感器目前还未被物理成功实现.因此,建立有效的记忆元件等效模型,以促进对记忆元件及其系统的仿真研究和应用研究是非常必要的.

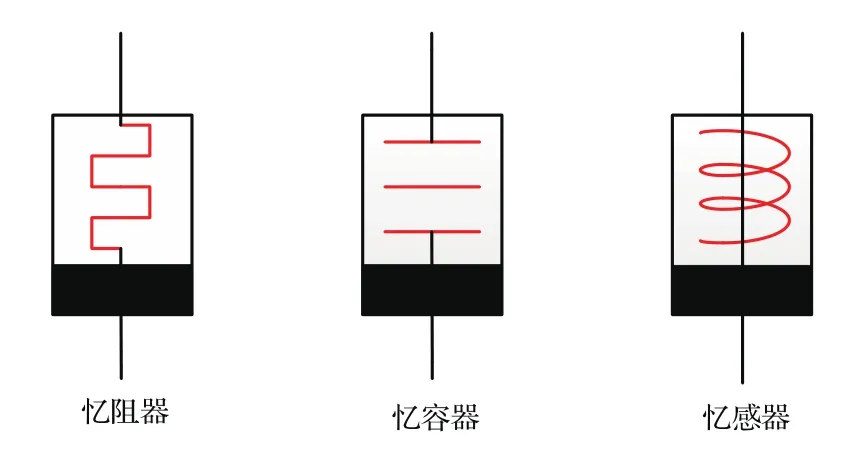
图1 忆阻器、忆感器和忆容器的电路符号Fig.1.Circuit symbols of memristor,memcapacitor,and meminductor.

近年来,关于记忆元件的理论模型及SPICE(simulation program with integrated circuit emphasis)模型相继被提出[10−15],随着对记忆元件应用研究的逐步深入,记忆元件的等效电路模型的建立也成为了一个研究热点.文献[16—18]对忆阻器、忆容器和忆感器的模拟电路仿真器进行了实现,基于这些仿真器的建立,一系列的应用研究也随之展开并取得了一定成果[19,20].在记忆元件的Simulink模型的研究中,目前主要取得以下成果.在忆阻器方面,2011年,胡柏林等[21]通过研究HP忆阻器模型,在理想HP线性忆阻器模型的基础上,构建了HP忆阻器的Simulink模型;2014年,宋卫平等[22]建立了基于受控源的双端口的HP忆阻器的Simulink仿真模型;2015年,段飞腾和崔宝同[23]对文献[21]中给出的HP忆阻器的数学模型进行了优化,通过引入窗函数将HP忆阻器的非线性特性加以表征,并构造了相应的Simulink模型.在忆容器方面,2011年,何朋飞等[24]依据文献[3]中给出的忆容器的数学方程,对忆容器的Simulink模型进行了构建,但没有对该数学模型中的阶跃函数进行分析和实现,导致该模型无法正确反映忆容值与其历史状态有关的记忆特性.类似地,2012年,张金铖等[25]从电路学的基本原理出发,推导了适用于忆感器的数学表达,并在此基础上建立了与其对应的忆感器的Simulink模型.

本文基于忆阻器、忆感器和忆容器的通用定义,通过对给定数学模型有效性的进一步研究,分别建立了三者的Simulink模型,所建立的模型均能体现记忆元件对系统状态变量以及历史状态的依赖性,通过对各模型在不同激励下的特性分析以及仿真实验验证,证实了所建立的模型具有记忆元件的典型特性以及各模型的有效性.

全文共分成6部分:第1部分介绍了记忆元件的发展历程,综述了在模型建立方面的背景和现状;第2部分对忆阻器、忆容器和忆感器的提出、通用数学定义以及它们的基本电路特性进行了系统的介绍;第3—5部分分别介绍了忆阻器、忆容器和忆感器Simulink模型的建立,并讨论了不同参数和不同激励对所建立的各类记忆元件模型的特性影响;第6部分对本文的内容进行了总结.

2 忆阻器、忆容器和忆感器的提出及其基本特性

2.1 忆阻器、忆容器和忆感器的提出

1971年,Chua[1]依据电路理论的完备性,首次提出了忆阻器的概念,并指出忆阻器作为第四种电路元件,可用于直接描述电荷q与磁通量φ之间的某种关系.基于此概念,忆阻器的数学定义即为

且当(1)式仅由电荷的单值函数来表示时,称为电荷控制型忆阻器,对应的数学表达式如下:

当(1)式仅由磁通的单值函数来表示时,称为磁通控制型忆阻器,其数学表达为

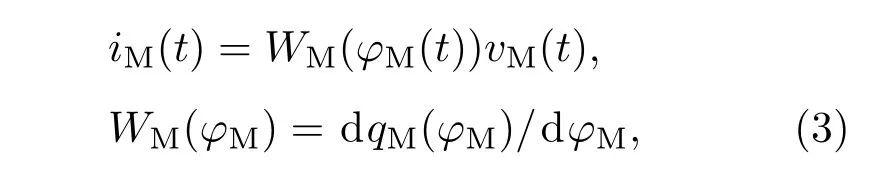
式中RM为忆阻值;WM为忆导值;iM(t),qM(t)为流经器件的电流量和电荷量;vM(t),φM(t)为器件两端的电压量和磁通量;M下标表示与忆阻器有关的变量.

2009年,Chua及其团队[26]通过定义以下两个新的变量,将有记忆特性的元件由忆阻器延伸至了忆阻系统,从而使有记忆特性的元件和传统电路元件一样,形成了一个完备的体系,如图2所示.

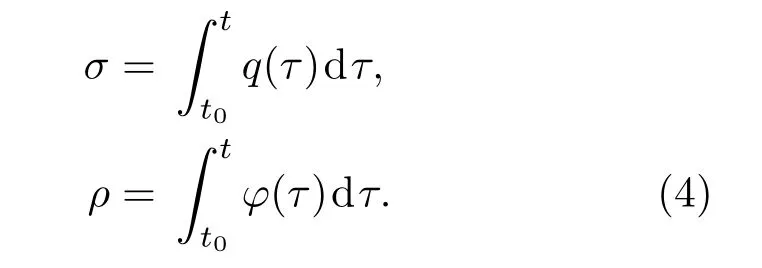
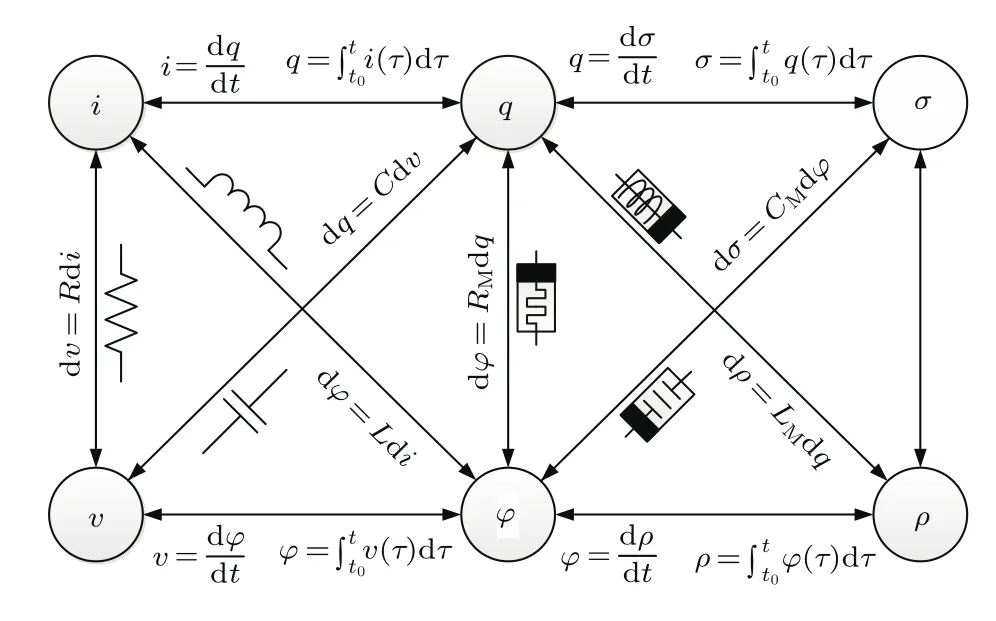
图2 传统电路元件与记忆元件间的关系Fig.2.Relationship between traditional circuit elements and the memory elements.

与忆阻器的分类相似,依据忆容器控制量的不同,可将其分为磁通控制型忆容器和电荷控制型忆容器,分别可由(5)和(6)式进行表示:

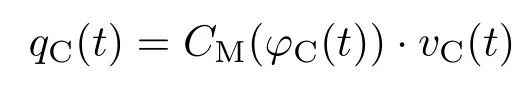
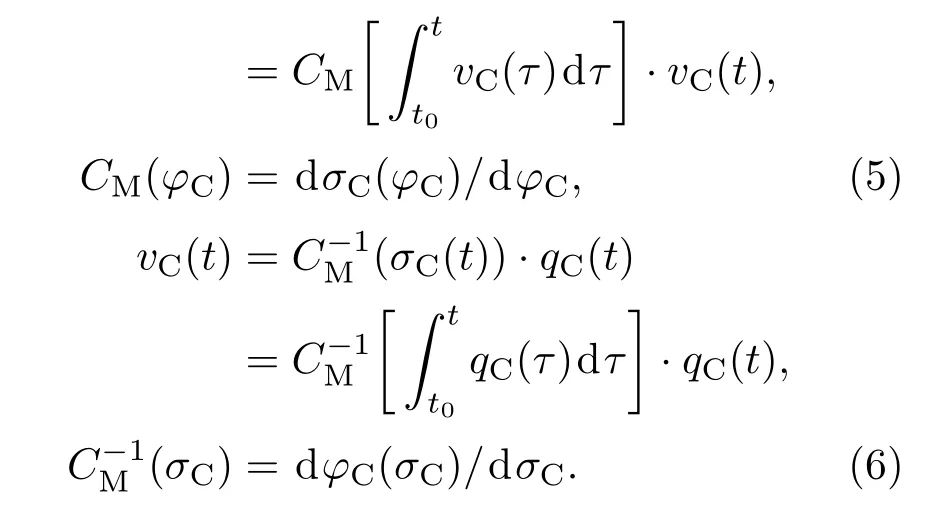
忆感器也可表示为(7)和(8)式所示的电流控制型和磁通控制型:

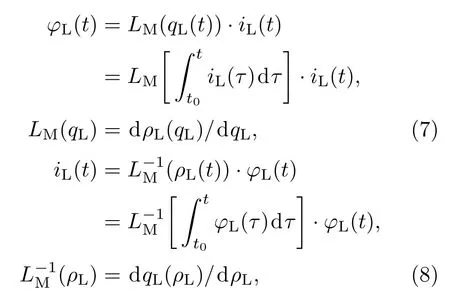
其中CM为忆容值;为忆容器的容纳值;qC(t)为流经忆容器的电荷量;vC(t),φC(t)为忆容器两端的电压量和磁通量;LM为忆感值;为忆感器的感纳值;qL(t),iL(t)为流经忆感器的电荷量和电流量;φL(t)为忆感器两端的磁通量;下标C和L分别代表忆容器和忆感器对应的变量.

2.2 忆阻器、忆容器和忆感器的通用数学模型

2009年,Di Ventra等[3]提出有记忆特性的元件不仅仅局限于忆阻器,实际上可以推广至忆容器和忆感器,并指出如果用x表示某个记忆元件的一组n维状态变量的集合,用u(t)和y(t)表示任意两个互补的本构变量(即电流、电荷、电压或磁通)且作为该系统的输入和输出,用g表示一个广义的响应函数,则可由(9)和(10)式定义一个通用的n阶记忆元件:

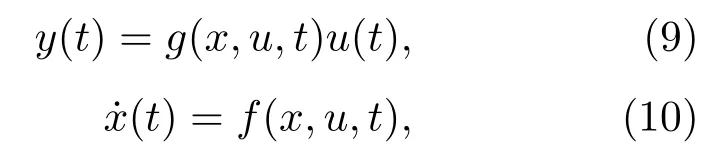
其中f是一个连续的n维向量函数,从物理意义上讲,若在t0时刻给定一个初始的状态u(t=t0),则(10)式具有唯一的解.依据上述理论,当u(t)和y(t)取作不同的互补变量时,可得到忆阻器、忆容器和忆感器的通用数学表达式如下.

1)忆阻器的通用数学定义

电流控制型忆阻器:

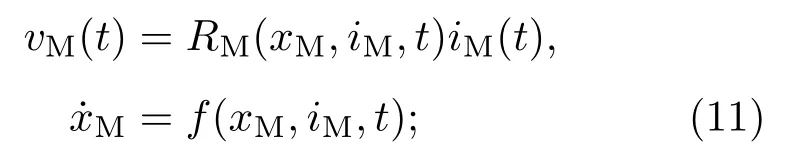
电压控制型忆阻器:

2)忆容器的通用数学定义

电压控制型忆容器:

电荷控制型忆容器:

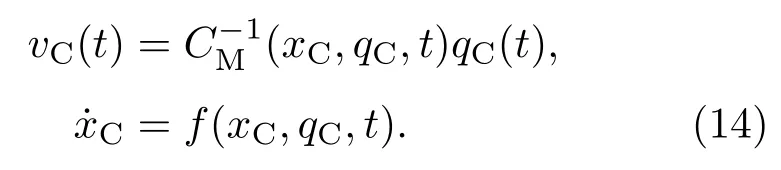
3)忆感器的通用数学定义

电流控制型忆感器:

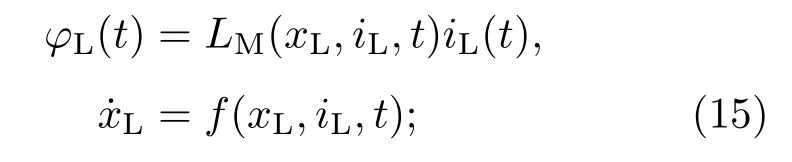
磁通控制型忆感器:

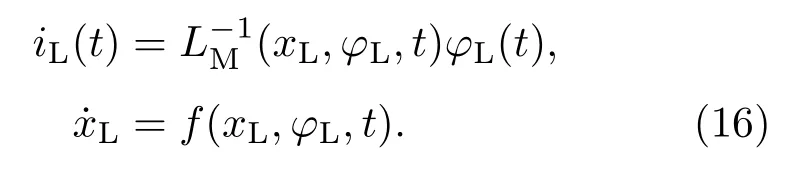
这里,xM,xC和xL分别表示忆阻器、忆容器和忆感器系统的无量纲状态变量.

2.3 忆阻器、忆容器和忆感器的基本电路特性

忆阻器、忆容器和忆感器共有如下的典型电路特性[2]:在正弦信号输入时,均存在各自固有内部变量间的滞后环关系,这种独特关系具体表现为忆阻器的vM-iM关系、忆容器的qC-vC关系以及忆感器的iL-φL关系.

此外,由上述定义(1)—(8)式可知,忆阻器、忆容器和忆感器各自的等效阻值、容值和感值均与其各自内部变量磁通、电荷以及它们对时间的积分有关,即与加在其两端的电压、磁通以及流过它们的电流、电荷的历史状态有关.且从以上定义式中可以得出,任何一种忆阻元件均应具有过零特性.以忆阻器为例,当iM(t)=0时,无论RM(qM(t))为何值,必然有vM(t)=0;对于忆容器,当vC(t)=0时,必然有qC(t)=0;类似地,忆感器也具有iL(t)=0,φL(t)=0的性质.因此,当记忆元件的输入信号为一定频率的过零周期信号时,其对应的特性曲线一定为经过坐标原点的滞回环曲线.

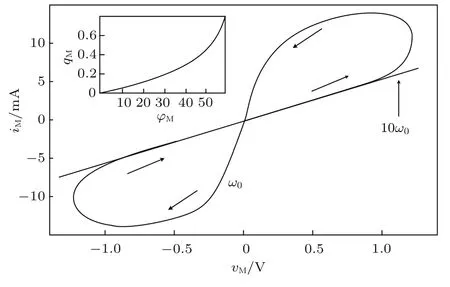
图3 HP忆阻器电压电流滞后环特性Fig.3.The vM-iMpinched loop characteristic of HP memristor.

2008年,HP实验室[4]借助于现代纳米技术的突破性成果,第一次成功地对忆阻器进行了物理实现,且通过实验对上述特性加以证实,得到了HP忆阻器具体的电路特性如下:当将一定幅值的正弦信号施加于忆阻器一段时间后,流过忆阻器的电流与施加于其上的电压间的关系,表现为如图3所示的紧致滞后环关系,且该滞后环的宽度依赖于输入电压的频率,当正弦信号的频率增加时,滞后环的宽度变窄,直至一条直线.

3 忆阻器Simulink模型的建立

3.1 忆阻器的Simulink模型设计

基于电压控制型忆阻器的通用数学定义(12)式,给定且令˙xM=f(xM,vM,t)表示为

函数时,可通过如图4(b)所示的电路对该模型进行仿真验证,得到该忆阻器在正弦电压作用下,其两端电压和流经忆阻器的电流呈现如图4(b)所示的滞后环特性,根据忆阻器特性的判定原则可知,该数学模型符合忆阻器的定义.这里,R1和R2分别代表忆阻器的下限饱和度和上限饱和度;α,β和VT是常数;θ函数表示单位阶跃函数.图4(a)所示为(17)式所表示的vM与f函数间的关系.

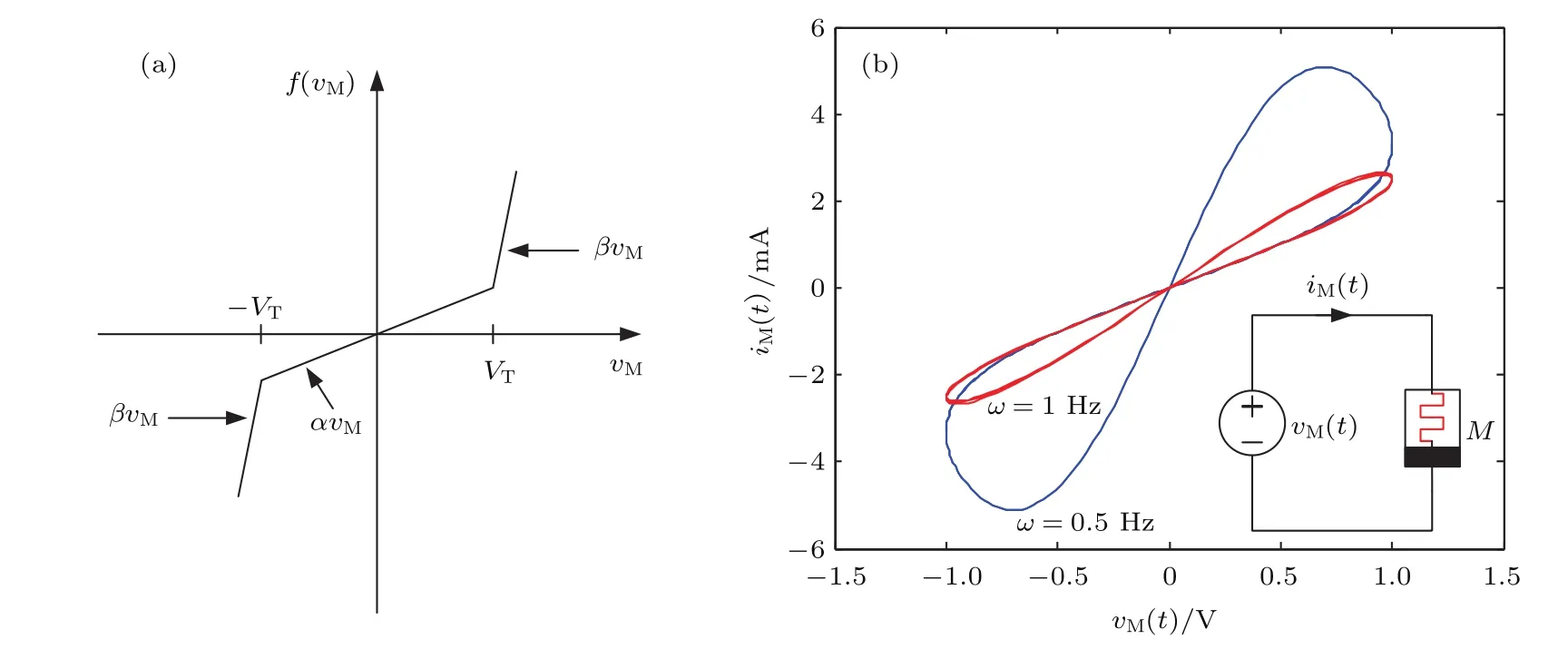
图4 (a)f函数与输入电压间的关系以及(b)基于f函数的忆阻器数学模型的验证Fig.4.(a)Curve of vM-f and(b)veri fication of memristor mathematical model based on f function.

基于以上关系,本文建立了忆阻器的Simulink仿真模型,如图5所示.其中θ函数所表示的单位阶跃函数通过两个开关比较模块(开关1和开关2)和4个常数模块进行实现,其中,常数模块5—8中的0和1分别表示阶跃函数的两个0和1状态.由图5可知,乘法器3的输出是(17)式中的˙xM,积分器的输出为xM,而开关1和开关2的输出是将xM的值与其内部设定的阈值进行比较,且当xM大于开关2所设定的忆阻器的上限饱和度R2时其输出为0,否则为1;而当xM小于开关1所设定的忆阻器的下限饱和度R1时其输出为0,否则为1.这样不仅实现了单位阶跃函数在等式中起到的作用,而且还正确地反映了忆阻器的等效忆导值与历史状态有关的特性,即表现出记忆元件具有的独特记忆特性,是该模型能够正确表征忆阻器性能的关键所在.

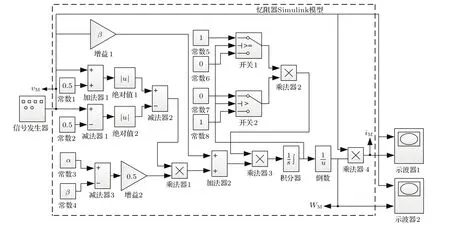
图5 忆阻器的Simulink模型及其验证电路Fig.5.Simulink model of the memristor and its veri fication circuit.

采用图5的实验电路验证上述模型的有效性,实验中所采用的具体参数如下:VT=0.5 V,α=500 Ω/(V·s),β=2α=1000 Ω/(V·s),R1=20 Ω,R2=500 Ω.信号发生器作为忆阻器等效电路的输入信号给定的参数为vM(t)=v0sin(2πωt),图5中示波器1显示的是忆阻器输入电压vM与流经其电流iM之间的关系,示波器2用于显示输入电压vM与等效忆导值WM间的变化关系.下面将根据给定输入信号的不同情况,讨论输入信号幅值、频率和波形对忆阻器特性的影响.

3.2 不同输入信号对忆阻器特性的影响

3.2.1 正弦输入信号的幅值变化对忆阻器特性的影响

当给定正弦输入信号频率f为0.5 Hz,幅值v0分别为0.5,0.8,1.0 V时,可得到该忆阻器模型的电压-电流曲线如图6所示,结果显示,随着输入信号幅值的增大,其电压-电流滞回曲线的轮廓也随之增大.

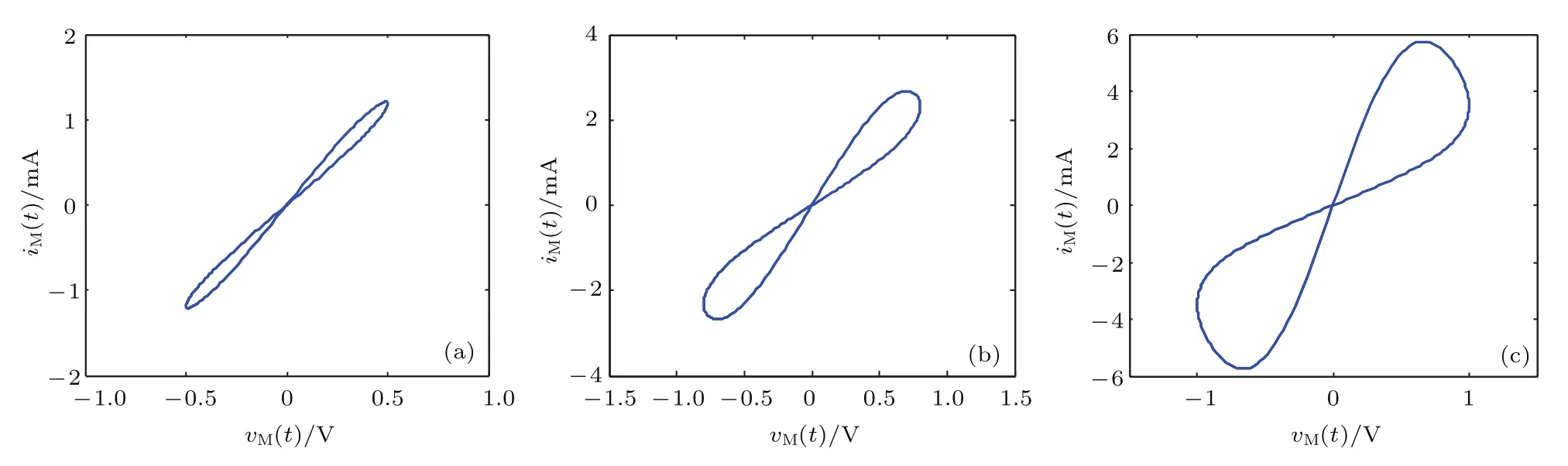
图6 输入正弦信号幅值的变化对忆阻器电压-电流特性的影响 (a)v0=0.5 V;(b)v0=0.8 V;(c)v0=1.0 VFig.6.In fluence of the change of input sinusoidal signal’s amplitude on the voltage and current characteristics of the memristor:(a)v0=0.5 V;(b)v0=0.8 V;(c)v0=1.0 V.

3.2.2 正弦输入信号的频率变化对忆阻器特性的影响

现给定忆阻器的正弦输入信号幅值v0=1.0 V时,考察改变该信号的频率f分别为0.5,1,3 Hz时忆阻器的电压-电流曲线.由图7可知,随着输入信号频率的不断增加,电压-电流滞回曲线越来越窄,当频率较大时该滞回曲线近似演变为一条直线.

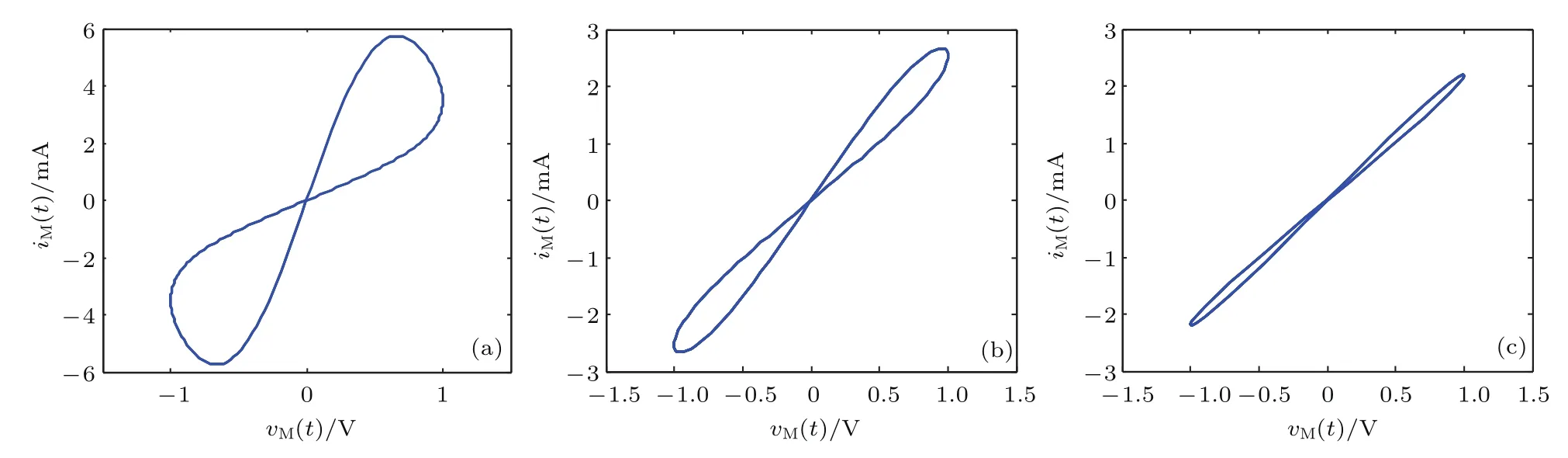
图7 输入信号频率的变化对忆阻器电压-电流特性的影响 (a)f=0.5 Hz;(b)f=1 Hz;(c)f=3 HzFig.7.In fluence of the change of input signal’s frequency on the voltage and current characteristics of the memristor:(a)f=0.5 Hz;(b)f=1 Hz;(c)f=3 Hz.

3.2.3 不同种类输入信号下忆阻器的电路特性

图8(a)—(c)所示分别为忆阻器等效模型在幅值v0=1 V,频率f=0.5 Hz的正弦波、方波和三角波为激励信号时对应的电压-电流特性曲线,图8(d)—(f)分别为各激励下对应的电压-忆导曲线.由图8的结果可以得出,任意过零的周期波作为激励时,该忆阻器模型的电压-电流关系均表现为经过原点的滞回曲线特性.

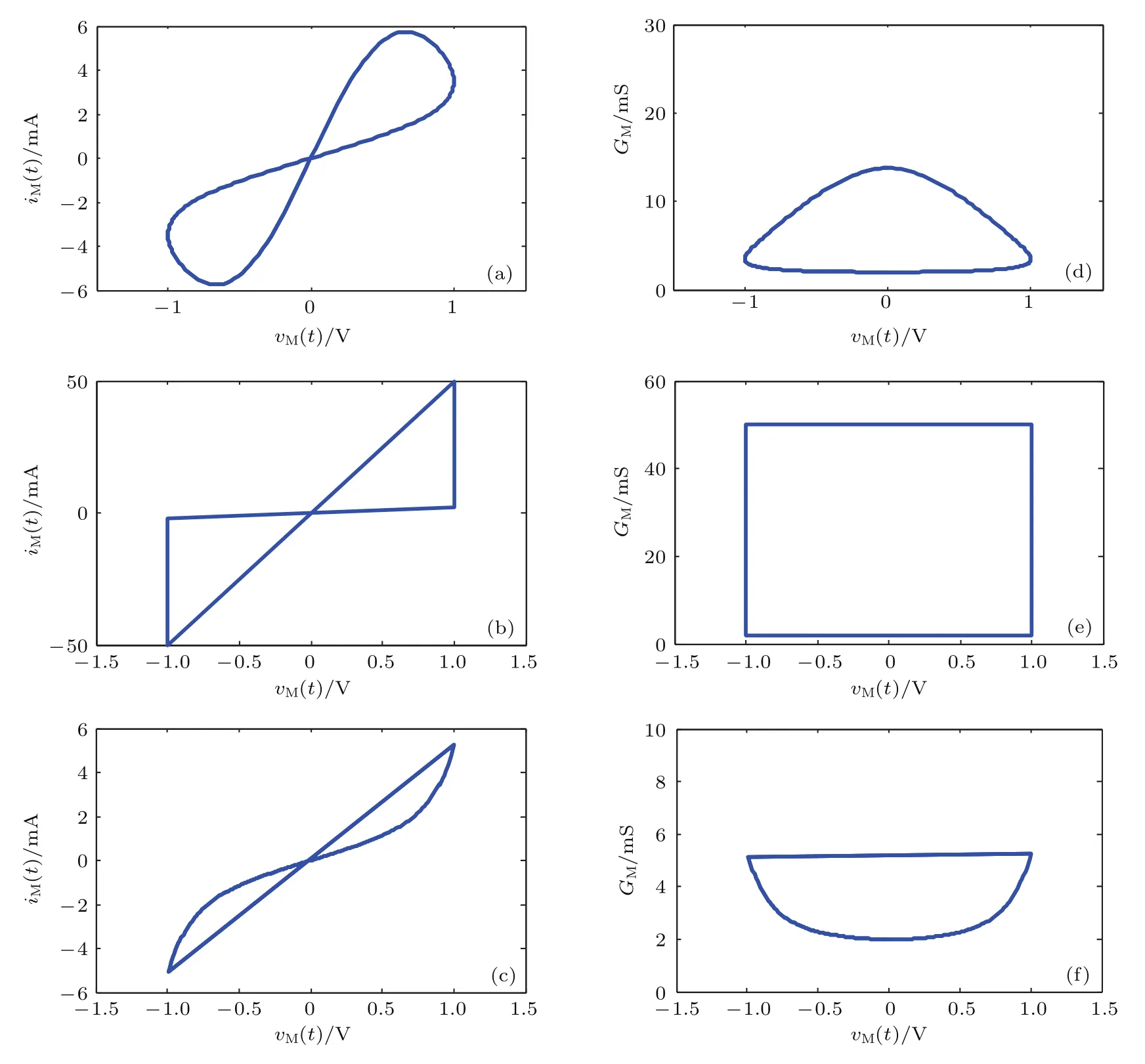
图8 不同种类输入信号下忆阻器的电路特性 (a)—(c)和(d)—(f)分别为正弦波、方波和三角波激励下的vM-iM和vM-GM特性曲线Fig.8.Circuit characteristics of memristor under different kinds of input signals:(a)–(c)and(d)–(f)The vM-iMand vM-GM relations under sinusoid,square and triangle waves.

4 忆容器的Simulink模型建立

4.1 忆容器的Simulink模型设计

根据n阶电压控制忆容系统的通用数学定义(13)式,令CM(xC,vC,t)=xC,同时给定C=f(xC,vC,t)为

函数(图9(a))时,通过如图9(b)中内嵌的电路对该模型进行仿真验证,得到该忆容器在该正弦电压作用下,其两端电压和流经忆容器的电荷量呈现出如图9(b)所示的滞后环特性,根据忆容器特性的判定原则可知该数学模型符合忆容器的定义.这里,C1和C2分别代表忆容器的下限饱和度和上限饱和度;α′,β′和是常数.

基于(13)和(18)式以及上述指定关系,可建立如图10所示的忆容器Simulink等效模型.模型中的θ函数采用了与忆阻器等效模型中相同的功能设计模块,目的在于实现忆容器作为记忆元件的独特的记忆特性,体现忆容器的等效忆容值与历史状态变量以及系统内部构成变量间的关系.图10中的仿真参数分别为β′=2α′=100 µF/(V·s),开关1 和开关2分别设定为1µF和20µF,积分器的初值为1µF,接下来进行Simulink仿真以验证该模型的有效性.

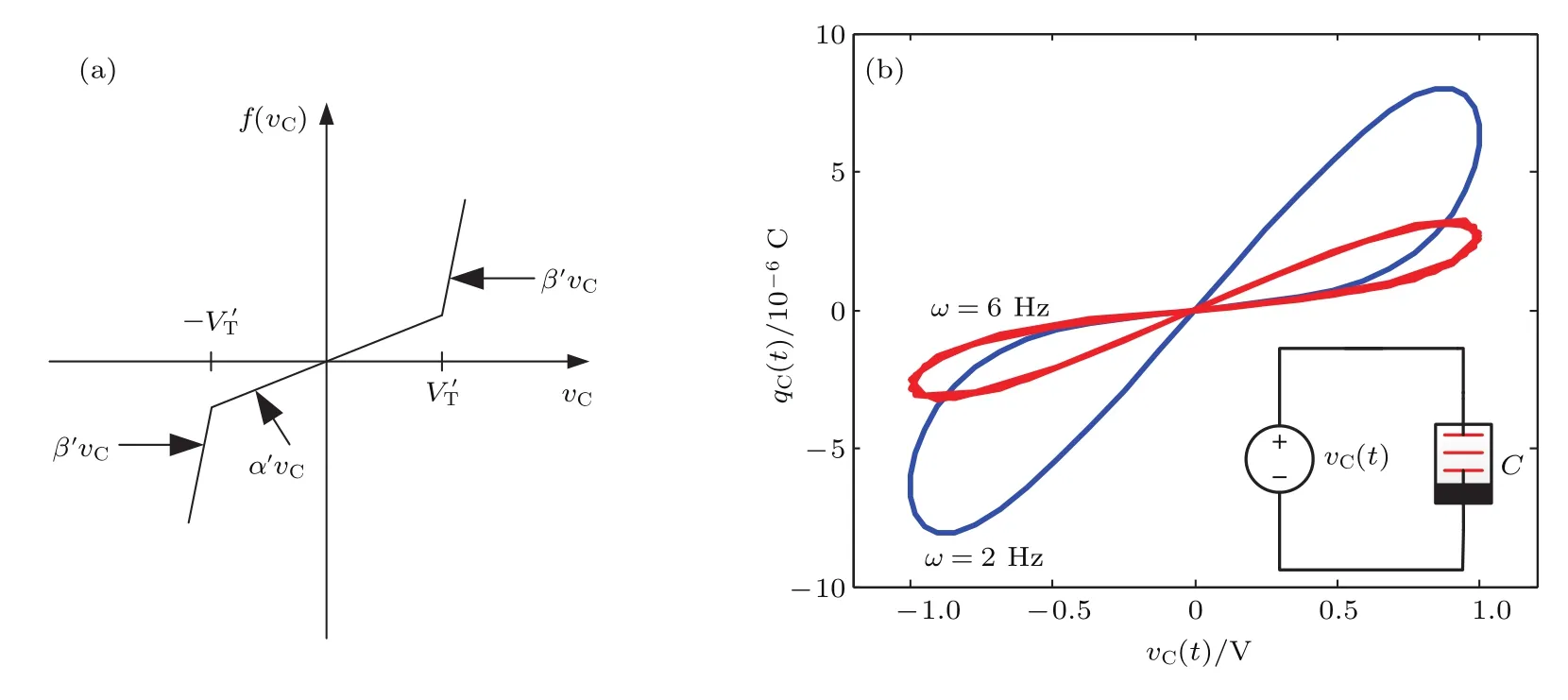
图9 (a)忆容器的f函数与输入电压间的关系以及(b)基于f函数的忆容器数学模型的验证Fig.9.(a)Curve of vC-f and(b)the veri fication of memcapacitor mathematical model based on f function.

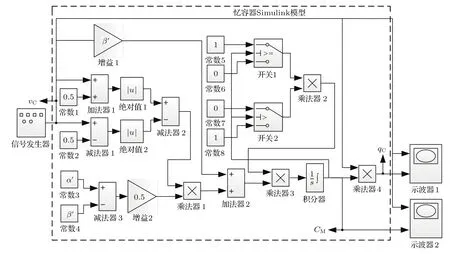
图10 忆容器的Simulink模型及其验证电路Fig.10.Simulink model of the memcapacitor and its veri fication circuit.

4.2 不同输入信号对忆容器特性的影响

采用图10中所示的验证电路对该电压控制型忆容器进行特性验证,基于忆容器表示的滞后环为其两端电压与流经忆容器电荷间的关系,本文采用的输入正弦电压为vC(t)=v0sin(2πωt),这样,根据(13)式即可通过中间变量xL,即系统等效的忆导值CM,计算得到电路中的电荷变量qC,从而绘制出忆容器的滞回特性曲线.

4.2.1 正弦输入信号的幅值变化对忆容器特性的影响

在仿真实验中,取输入正弦信号的幅值分别为0.8,1.0和1.2 V,并令t=0时,C=1µF,可得到忆容器在相应各幅值下的电压-电荷曲线如图11所示.可以从图11看出,随着幅值的增大,忆容器的电压-电荷滞回曲线的边界增大.

4.2.2 正弦输入信号的频率变化对忆容器特性的影响

与忆阻器的特性相类似,当给定忆容器两端电压vC(t)=v0sin(2πωt)的频率分别为0.2,2和10 Hz,考查幅值v0=1.0 V前提下的电压-电荷曲线如图12所示.由图12结果可知,随着输入信号频率的增加,其电压-电荷紧致滞后曲线会越来越窄,直到接近于一条直线,即表明了忆容器在输入信号频率接近无穷大时表现为一个线性电容,在低频率输入信号作用下,其显现为一个非线性的电容.

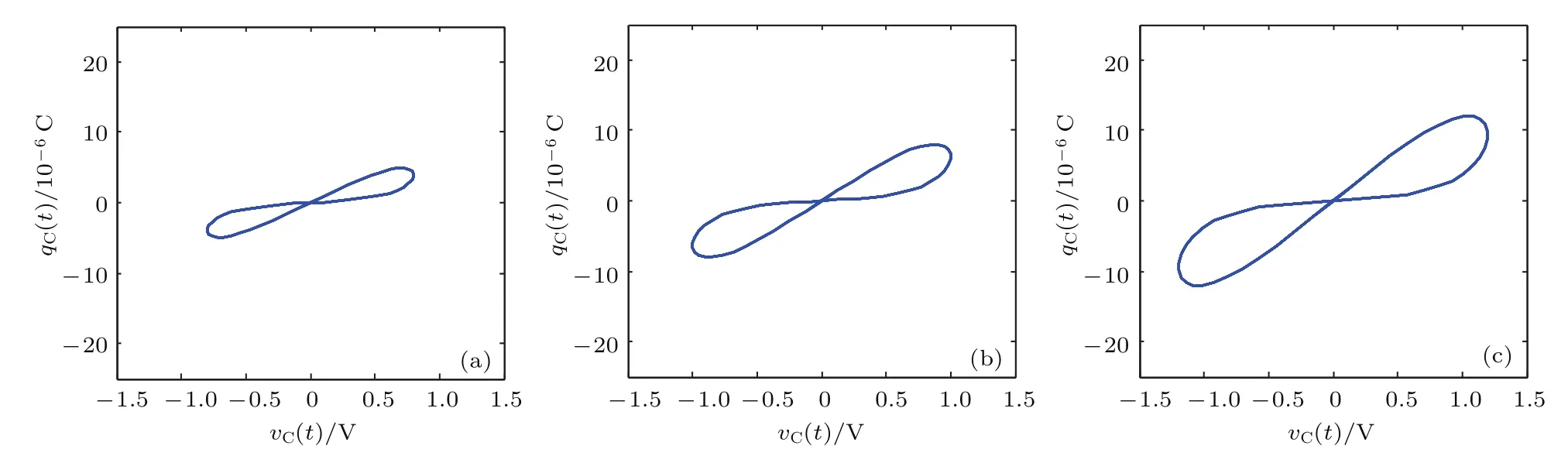
图11 正弦输入信号的幅值变化对忆容器特性的影响 (a)—(c)对应的输入信号幅值分别为0.8,1.0和1.2 VFig.11.In fluence of the change of input sinusoidal signal’s amplitude on the characteristics of the memcapacitor:(a)–(c)The characteristics under 0.8,1.0 and 1.2 V respectively.

图12 正弦输入信号的频率变化对忆容器特性的影响 (a)—(c)对应的输入信号频率分别为0.2,2和10 HzFig.12.In fluence of frequency variation of sinusoidal input signal on the characteristics of memcapacitor:(a)–(c)The characteristics under 0.2,2 and 10 Hz respectively.

4.2.3 不同种类输入信号下忆容器的电路特性

图13为给定忆容器输入电压分别为幅度v0=1 V,频率为2 Hz的正弦波、方波和三角波时所得到电压-电荷以及电压-忆容曲线.其中,图13(a)—(c)分别对应不同输入波形下的电压-电荷曲线,图13(d)—(f)分别各波形对应的电压-忆容曲线.

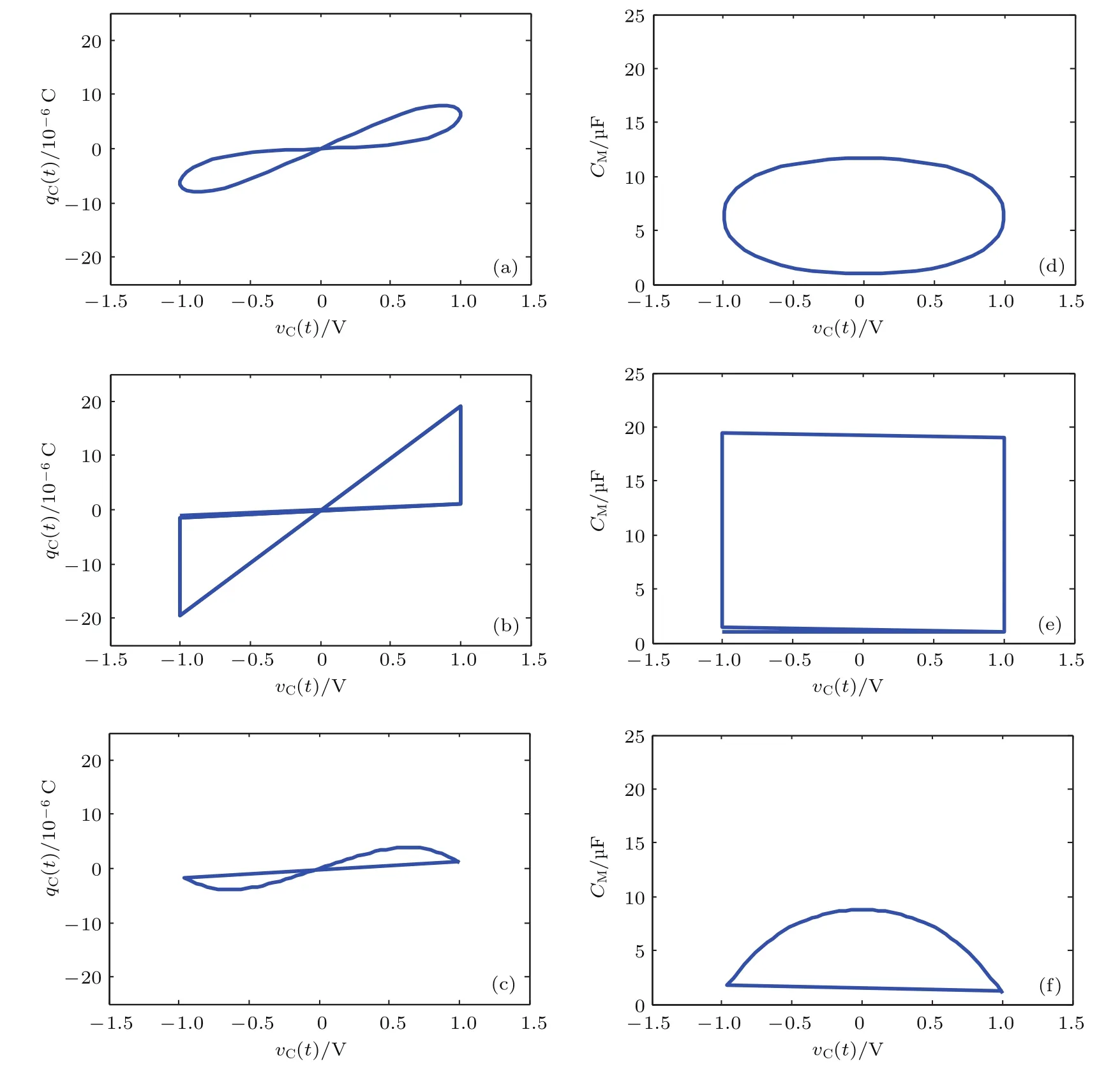
图13 不同种类输入信号下忆容器的电路特性 (a)—(c)和(d)—(f)分别为正弦波、方波和三角波激励下的vC-qC和vC-CM特性曲线Fig.13.Circuit characteristics of memcapacitor under different kinds of input signals:(a)–(c)and(d)–(f)The vC-qCand vC-CMrelations under sinusoid,square and triangle waves.

5 忆感器的Simulink模型建立

5.1 忆感器的Simulink模型设计

文献[3]虽然给出了n阶磁通控制型忆感系统的定义如(19)式所示,但并没有给出具体表征忆感器的具体数学模型,本文中遵循以上两类记忆器件等效数学模型的建立方式,首次给出了基于忆感器通用数学定义的忆感器的数学模型.

首先,令同时给定状态变量xL与输入磁通信号之间的关系如下:

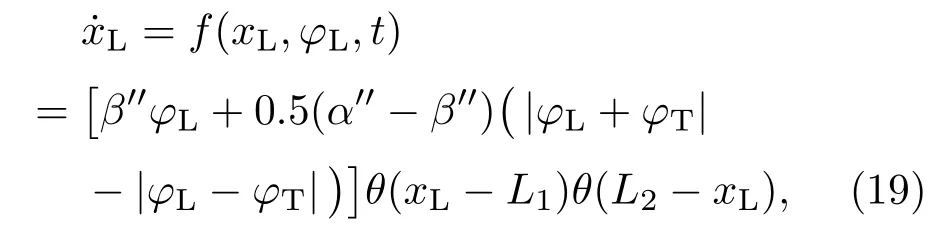
其中,L1和L2分别代表忆感器的下限饱和度和上限饱和度;α′′,β′′和φT均是常数.由于忆感器与忆阻器和忆容器类似,它的等效电感值与状态变量以及历史状态有关,因此,(19)式中也应包含θ函数,用以实现并体现其独有的记忆特性.应用图14(b)中的内嵌电路,现对该忆感器等效模型进行仿真验证,仿真中采用正弦磁通信号作为该等效电路的输入,考查流经其电流与输入磁通信号的关系曲线,得到了如图14(b)所示的磁通-电流滞回曲线,依据忆感器特性的判定规则,可得出该数学模型符合忆感器的定义及基本电路特性,其中,图14(a)所示为f函数所表示的状态变量对时间的导数与其内部磁通间的关系.

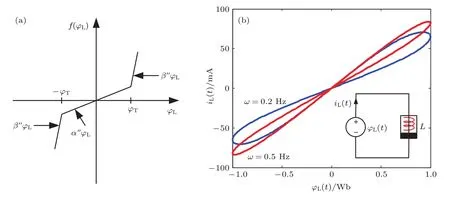
图14 (a)忆感器的f函数与输入磁通间的关系以及(b)基于f函数的忆感器数学模型的验证Fig.14.(a)Curve of φL-f and(b)the veri fication of meminductor mathematical model based on f function.

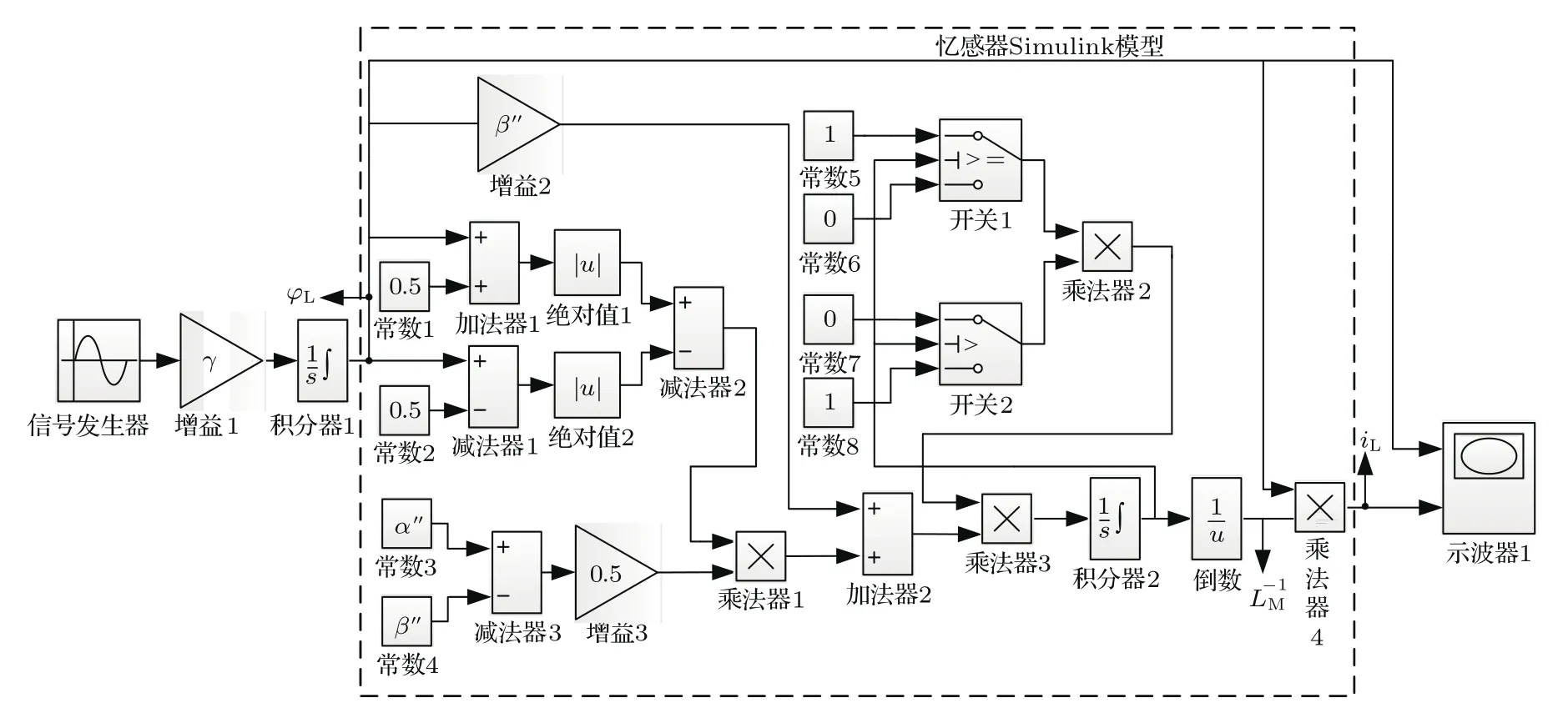
图15 忆感器的Simulink模型及其验证电路Fig.15.Simulink model of a meminductor and its veri fication circuit.

基于以上关系,本文建立了通用忆感器的Simulink模型,如图15所示.为测试该模型的有效性,依据忆感器的本构关系,需要以磁通作为忆感器的输入信号,验证周期过零磁通经过忆感器时,其电流与磁通间的关系是否表现为过零的i-φ滞回曲线特性.为此,这里将信号发生器的输出设置为vL(t)=v0cos(2πωt),以使得信号发生器后面连接的一个增益和积分器输出满足测试忆感器特性的磁通输入信号φL(t)=v0sin(2πωt),即一个周期的交变信号.仿真参数具体如下:φT=0.5 Wb,α′′=5 H/(V·s),β′′=2α′′,L1=10 H,L2=100 H,这样,在积分器2的输出端得到的即为系统状态变量的等效值xL,为得到系统的等效电流iL,需要对xL取倒数,以得到的等效值,再通过乘法器4实现这样就得到了忆感器的等效电流iL,将其与忆感器输入磁通量分别输入至示波器1,即可得到忆感器的两个构成变量间的变化关系,从而实验对该模型有效性的验证.

5.2 不同输入信号对忆感器特性的影响

5.2.1 输入信号幅值对忆感器特性的影响

当给定忆感器输入电压vL(t)=v0cos(2πωt)时,给定γ=2πω=0.4π,即f=0.2 Hz时,等同于给定忆感器的磁通输入信号为φL(t)=v0sin(2πωt),设定初始值t=0时,L=80 H,可在图15示波器1上得到v0分别取为0.8,1.0和1.2 V时的磁通-电流曲线,如图16(a)—(c)所示.可以看出,随着输入信号幅值的增大,磁通-电流的滞回曲线的变化幅度也随之增大.

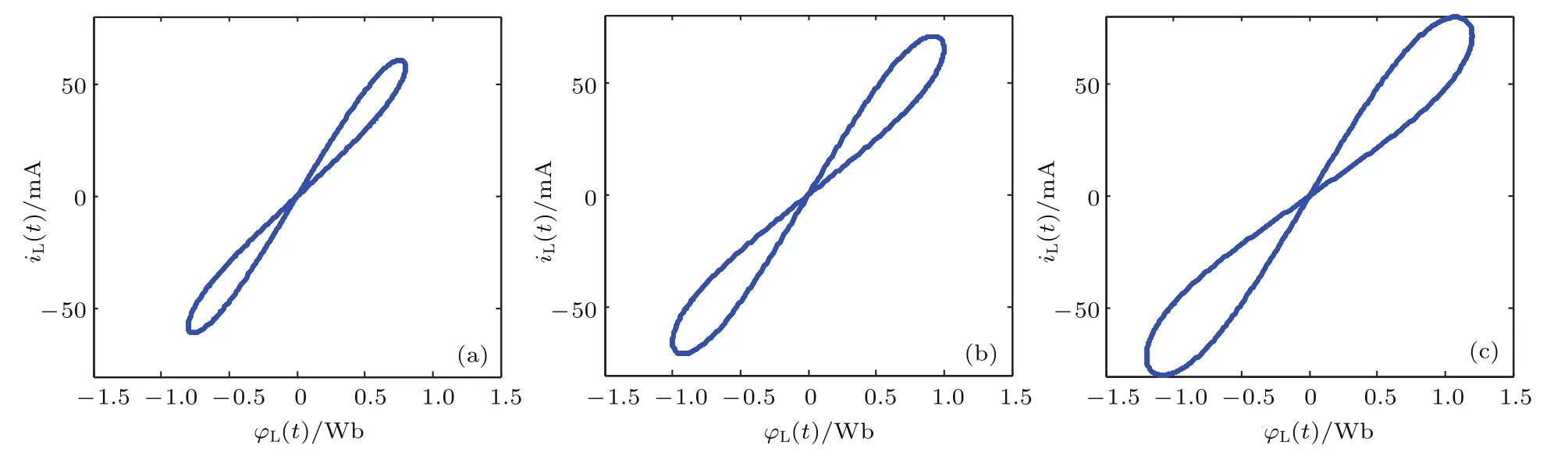
图16 输入信号幅值对忆感器特性的影响 (a)v0=0.8 V;(b)v0=1.0 V;(c)v0=1.2 VFig.16.In fluence of the input signal amplitude on the meminductor characteristic:(a)v0=0.8 V;(b)v0=1.0 V;(c)v0=1.2 V.

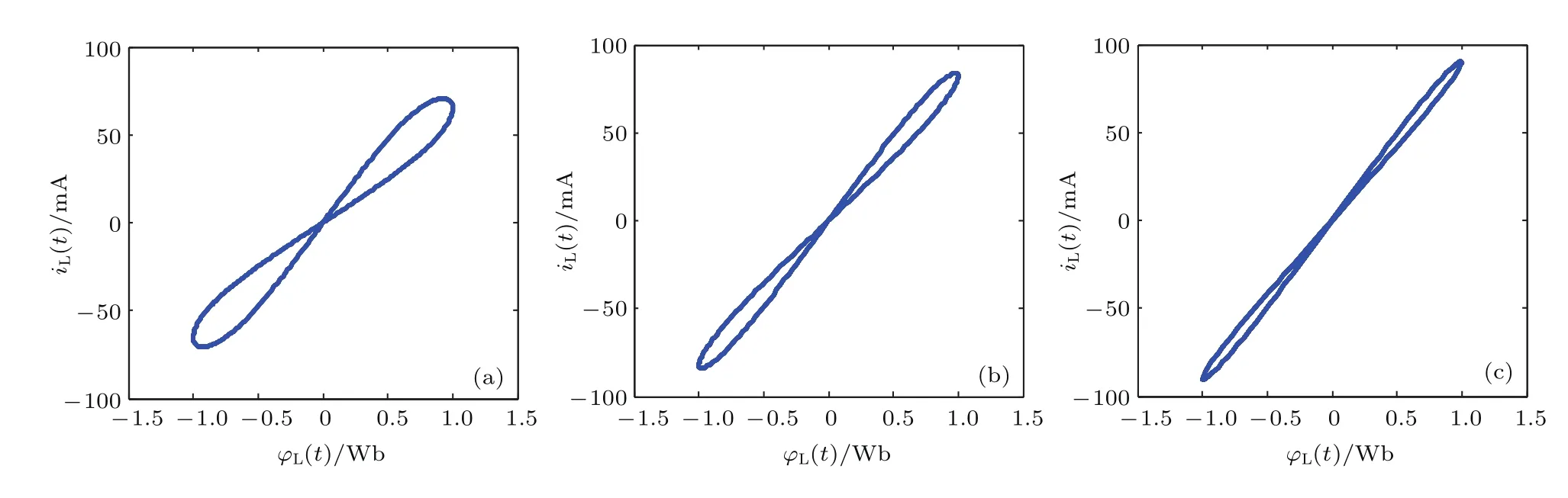
图17 输入信号频率对忆感器特性的影响 (a)f=0.2 Hz;(b)f=0.5 Hz;(c)f=1 HzFig.17.In fluence of the input signal frequencies on the meminductor characteristic:(a)f=0.2 Hz;(b)f=0.5 Hz;(c)f=1 Hz.

5.2.2 输入频率对忆感器特性的影响

给定忆感器输入电压vL(t)=v0cos(2πωt),令v0=1.0 V,分别将给定γ=2πω设定为给定0.4π,π和2π,即可得f分别为0.2,0.5和1 Hz的输入磁通输入信号为φL(t)=v0sin(2πωt),初始状态设定为t=0时,L=10 H,可在图15示波器1上得到f分别取为0.2,0.5和1 Hz时的磁通-电流曲线,如图17(a),(b),(c)所示.可以看出,随着输入信号频率的增大,磁通-电流的滞回曲线变得越来越窄,直到一条斜线.

以上两组实验结果表明,该模型符合忆感器的定义,且完全满足忆感器的电路特性,证实了该模型的有效性.

6 结 论

本文介绍了忆阻器、忆感器和忆容器的通用数学模型,并在此基础上,对三者的Simulink仿真模型进行了精确的搭建.模型中首次引入两个开关比较模块用以实现阶跃函数,并借助于此功能模块正确地使三种记忆元件的Simulink模型能够真实反映记忆元件等效值与各自内部变量的历史状态有关的特性,即表现出记忆元件具有的独特记忆特性.通过对模型进行了不同参数和不同激励的仿真,得到了三种记忆元件独有的电路特性,验证了模型的有效性和可实用性,为今后基于忆阻器、忆容器和忆感器Simulink的仿真研究和应用研究奠定基础.

参考文献

[1]Chua L O 1971IEEE Trans.Circuit Theory18 507

[2]Chua L O 2008Memristor and Memristive System SymposiumBerkeley,USA,November 21,2008

[3]Di Ventra M,Pershin Y V,Chua L O 2009Proc.IEEE97 1717

[4]Strukov D B,Snider G S,Stewart D R,Williams R S 2008Nature453 80

[5]Faruque K A,Biswas B R,Rashid A B 2017Circuits Syst.Signal Process.36 1

[6]Ali M S,Saravanan S 2017Chin.J.Phys.55 1953

[7]Di Marco M,Forti M,Pancioni L 2017IEEE Trans.Cybernetics47 2970

[8]Wang X Y,Iu H H C,Wang G Y,Liu W 2016Circuits Syst.Signal Process.35 4129

[9]Njitacke Z T,Kengne J,Fotsin H B,Negou A N,Tchiotsop D 2016Chaos Solitons Fractals91 180

[10]Pershin Y V,Di Ventra M 2010IEEE Trans.Circuits Syst.I57 1857

[11]Biolek D,Biolek Z,Biolkova V 2011Radioengineering20 228

[12]Sah M P,Budhathoki R K,Yang C,Kim H 2014J.Semiconductor Technol.Sci.14 750

[13]Biolek D,Biolek Z,Biolkova V 2009European Conference on Circuit Theory and DesignAntalya,Turkey,August 23–27,2009 p249

[14]Biolek D,Biolek Z,Biolkova V 2010Electron.Lett.46 520

[15]Biolek D,Biolek Z,Biolkova V 2011Analog Integeated Circuit Signal Process.66 129

[16]Wang X Y,Fitch A L,Iu H H C,Sreeram V,Qi W G 2012Chin.Phys.B21 108501

[17]Yu D S,Zhou Z,Iu H H C,Fernando T,Hu Y H 2017IEEE Trans.Circuits Syst.II63 1101

[18]Sah M P,Budhathoki R K,Yang C,Kim H 2014Circuits Systems Signal Process.33 2363

[19]Wang X Y,Fitch A L,Iu H H C,Qi W G 2012Phys.Lett.A376 394

[20]Liang Y,Yu D S,Chen H 2013Acta Phys.Sin.62 158501(in Chinese)[梁燕,于东升,陈昊 2013物理学报62 158501]

[21]Hu B L,Wang L D,Huang Y W,Hu X F,Zhang Y Y,Duan S K 2011J.Southwest Univ.33 50(in Chinese)[胡柏林,王丽丹,黄艺文,胡小方,张宇阳,段书凯2011西南大学学报33 50]

[22]Song W P,Ding S C,Ning A P 2014J.Taiyuan Univ.Sci.Technol.35 23(in Chinese)[宋卫平,丁山传,宁爱平2014太原科技大学学报35 23]

[23]Duan F T,Cui B T 2015Res.Prog.Solid State Electron.3 231(in Chinese)[段飞腾,崔宝同 2015固体电子学研究与进展3 231]

[24]He P F,Wang L D,Duan S K,Li C D 2011J.Univ.Electron.Sci.Technol.China40 648(in Chinese)[何朋飞,王丽丹,段书凯,李传东2011电子科技大学学报 40 648]

[25]Zhang J C,Li C D,Li C B 2012Res.Prog.Solid State Electron.32 239(in Chinese)[张金铖,李传东,李超辈2012固体电子学研究与进展32 239]

[26]Ventra M D,Pershin Y V,Chua L O 2009Proc.IEEE97 1371