基于金属狭缝阵列的各向异性偏振分束器∗

马婧 刘冬冬 王继成3) 冯延

1)(江南大学理学院光电科学与工程系,无锡 214122)

2)(徐州工程学院数学与物理科学学院,徐州 221018)

3)(东南大学,毫米波国家重点实验室,南京 210096)

1 引 言

类似金属结构的超材料具有独特的电磁特性,例如突破衍射极限的光收集性能[1]、超强传输性能[2]、等离子体彩色滤波[3]、调控反射或透射光束的传播方向[4,5]等.三维超材料与二维超表面成为光子学领域的研究热点.对于二维超表面结构,由于谐振特性的存在,需要精确地布置其谐振天线的方向和形状才可获得所需的梯度折射率等重要研究参数.对于多层三维超材料,其制造工序复杂,可利用的带宽窄,金属的固有损耗致使光学效率不高[6,7].因此,设计具有良好性能的高密度光栅元件对于光信息处理系统是至关重要的[8].

在光学系统中往往需要对极化偏振态进行控制,利用传统的偏振分束器(polarization beam splitter,PBS),如Wollaston棱镜和波片等,可以使两个入射的正交偏振光的传播方向分离.但是传统PBS的结构复杂且无法满足宽带特性的要求[9−11].随着光栅矢量理论的发展,基于高空间频率且周期与入射波长相当的微纳金属-介质光栅逐渐成为偏振衍射理论方向的研究热点[12−14].通过金属-介质光栅可将横电(TE)和横磁(TM)偏振光分离成方向和衍射级次均不同的两束反射光,展现出了纳米光学材料结构的极化负反射(negative re flection,NR)和镜面反射(specular re flection,SR)特性[15].该光栅具有体积小、效率高以及带宽宽等优点,在不依赖于谐振耦合机制的情况下,灵活易调谐,有着较为广泛的发展前景[16,17].

本文主要提出了一种基于金属狭缝阵列的各向异性PBS.讨论了入射角从20◦—70◦变化的NR光谱特性,可知入射的TM光发生了强烈的NR,而TE光的NR很弱,并随着波长的增加而急剧下降.研究了偏振分束光栅的理想NR现象和完美对称响应,得到了理想NR点的取值范围并加以验证.通过计算不同偏振光入射时的NR和SR光谱反射率和比值,得到了两种情形下的消光比,其最高可达106.

2 理论与结构设计

基于表面等离子体激元的偏振分束器结构如图1所示,首先通过纳米压印的工艺技术在硅衬底上放置了聚甲基丙烯酸甲酯(polymethyl methacrylate,PMMA)光栅,光栅周期P为750 nm,狭缝宽w1为300 nm,光栅高度h1为200 nm.而后,通过电子束蒸镀(E-beam)法在纳米压印的光栅上沉积厚度为h2=50 nm的金(Au)膜,除了在PMMA的顶部和凹槽中形成厚度为50 nm金膜之外,PMMA阵列的侧壁涂覆厚度为w3=35 nm的金.当以不同偏振态和不同角度的光入射时,理想情况下,会出现NR和SR两种不同的情形.

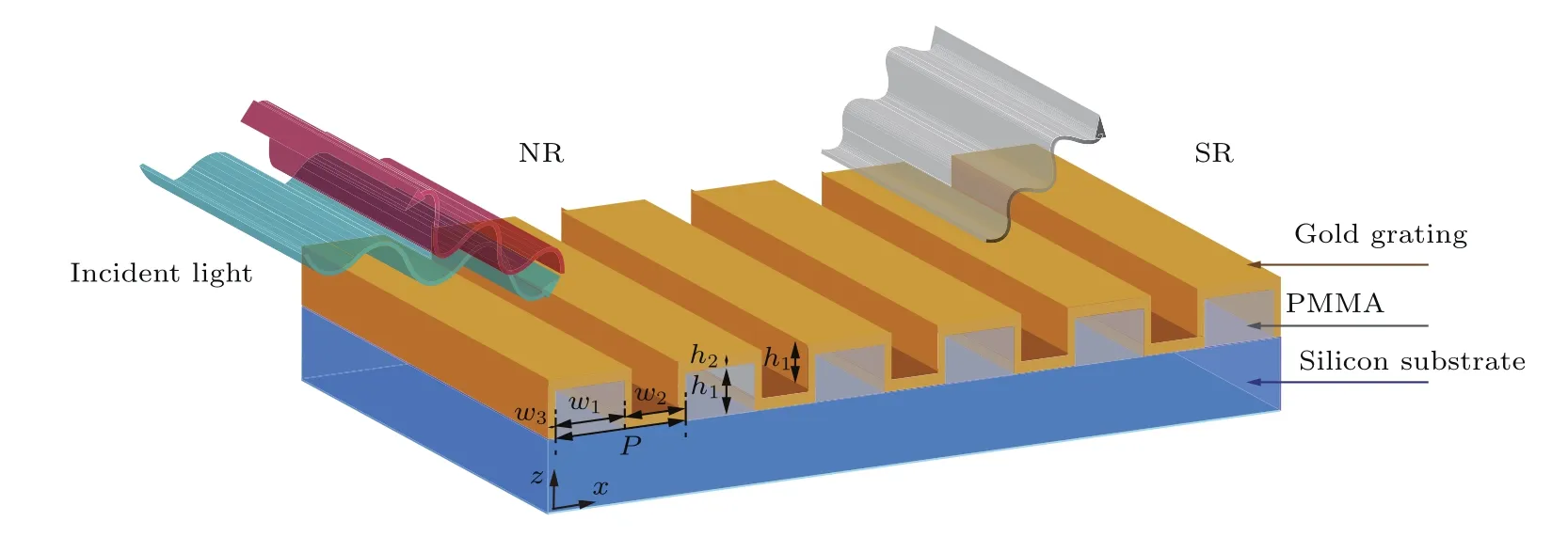
图1 基于金属聚合物阵列结构的PBS示意图(结构参数:P=750 nm,h1=200 nm,h2=50 nm,w1=300 nm,w2=450 nm,w3=35 nm)Fig.1.Schematic diagram of polarization beam splitter based on metal-polymer array structure(structure parameter:P=750 nm,h1=200 nm,h2=50 nm,w1=300 nm,w2=450 nm,w3=35 nm).

图2为产生两种不同反射现象的原理图.这里,将反射为负的第一衍射级定义为NR,反射为零的衍射级定义为SR,入射光波长λ均为1µm保持不变.图2(a)中TM光以等离子体波导模式进入狭缝,由于界面的不均匀产生的横向动量,TM光被底部金膜剧烈反射(NR),反射光线与入射光线位于法线同侧,如红色箭头所示.同时基于等离子体共振原理会产生相较于NR强度较弱的SR,如灰黑色箭头所示.图2(b)中TE光不能进入狭缝,原因在于金属表面自由电子发生振荡时,电场方向与光栅方向平行的TE光能够激发电子沿光栅方向引起振荡,从而主要发生SR;电场方向与光栅方向垂直的TM光因不规则表面和周期性结构无法激发自由电子振荡,从而主要发生透射[18,19].

为了有效地描述反射光束,提出了超表面所支持的局部反射系数解析表达式,以便在平面x-z中提高入射角度θ0的反射效率,沿与表面垂直的方向:

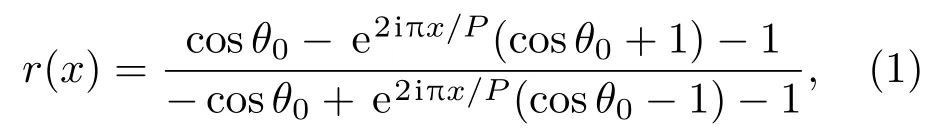
其中P是光栅周期,θ0是光束的入射角.一般而言,光栅表面的最佳反射系数也会影响局部振幅的调制.然而,入射光束和散射光束之间的精确阻抗匹配保证了光栅结构中100%的光波转换效率.

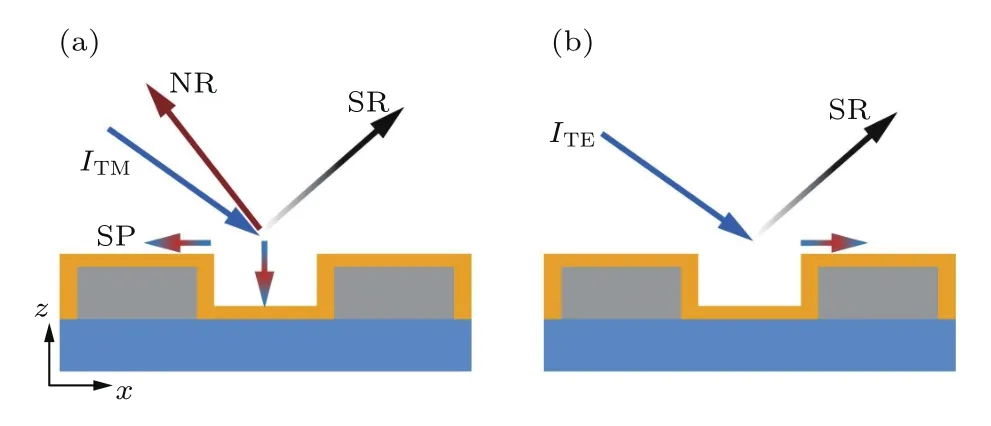
图2 PBS工作原理图 (a)由于不均匀界面导致的横向动量,大部分入射的TM偏振光ITM在法线同侧产生NR,少部分经表面等离子共振(suface plasmon resonance,SPR)产生SR;(b)由于界面处的动量守恒,TE偏振光ITE产生理想的SRFig.2.Schematic of polarization beam splitter:(a)Due to the lateral momentum caused by the uneven interface,most incident TM polarized light ITM produces NR on the same side of the normal,and a small part of the SPR produces SR;(b)due to the momentum conservation at the interface,TE polarization ITEproduces the ideal SR.

衍射区域的不同边界线表示不同入射角度下光栅的最大负一级衍射波长,即λG=P×(1+sinθ0),当入射角增大时,衍射区向长波方向移动,进而可以根据需要调谐波长.而NR角的大小会随着入射角变化呈现出非线性变化,两者间的变化关系可用一阶衍射光栅方程表示:

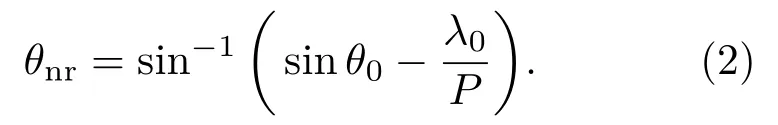
该设计结构采用Drude模型来描述金的介电损耗[20],即

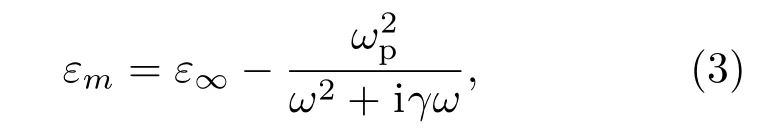
其中ε∞=9,ωp=1.3673×1016Hz,γ=1.0027×1014Hz.x和y方向看作是周期性边界条件.

3 数值模拟与结果分析

为了探讨理论的可行性,首先通过改变不同偏振光下的入射角大小,拟合出入射角从20◦—70◦变化的NR光谱,如图3所示,不同的颜色表示不同的入射角,圆点连线和实线分别表示TM和TE光入射时的模拟结果.可明显看出,入射的TM光将沿原路发生NR,且最大反射率大于0.9,而TE光的NR很弱,且随着波长的增加而急剧下降.根据负一级衍射波长公式λG=P×(1+sinθ0)可知,当θ0=20◦时,衍射波长近似为1µm.θ0增大,衍射波长增大,光谱呈现出红移的趋势,且θ0越大,TM光的反射率越低,NR效果越弱[21].

图3 TM和TE入射时的NR光谱图Fig.3.NR spectra of TM and TE incidence.

对于不同入射角下的TM偏振光,−1级衍射产生的阵列表面角度色散曲线如图4所示.在入射角范围(20◦<θ0<70◦)内,拟合曲线随入射角的增大而趋于平缓,即在远离正入射的宽角度范围上实现了NR.这种宽角度响应出现的原因在于:表面动量不随入射角变化,且趋于负无穷,确保了反射光束的角度在宽角度范围内实现反相.通常,所设计的分束器入射角越接近45◦,NR效果越明显.而接近入射角的下限截止值(θ0=18◦)时近乎无NR,因此在实际应用中可根据需要进行设计调整.图中两垂直虚线的交点(41.84◦,−41.84◦),(−41.84◦,41.84◦)恰好满足P=λ/(2sinθ0),即为理想的NR点,此时的耦合效率达到100%.

图4 TM偏振光入射时阵列表面的NR角度色散曲线Fig.4.NR angle dispersion curve of the array surface with the TM polarized light.

图5(a)所示为反射面的完美对称响应,若将入射光(θ0)的NR率设定为x%,则必定能确保镜面方向(θsr=θ0)可产生(100−x)%的耦合效率.当入射光翻转并且沿镜面方向照亮时,(100−x)%的效率恰好可以被耦合到θ0方向,剩余x%则必须通过惟一的散射通道散射.考虑到该周期不受入射方向的影响,并且结构仅允许两个衍射级,所有剩余能量(x%)将耦合到反射光束上.本文将金属光栅看作是能够实现双功能的反射镜元件,即可用于TE偏振和TM偏振的双端口高效分束器.为了更直观地分析TM和TE偏振光对两类反射效果的影响,图5(b)给出了入射角与反射峰值波长的关系曲线.基于TE和TM模式分裂的特性,当入射光角度(θ0)增大,TM光入射时所产生的两类反射峰波长变化很小,且与入射光波长大小近似.而TE光入射时所产生的两类反射峰波长会产生明显的红移(蓝移),两条反射峰彼此分离,更有利于对光与光栅结构相互作用的调谐.

基于偏振结构的设计,利用严格耦合波法仿真了不同偏振光入射时的NR和SR光谱图,并通过计算得到了两种情形下的消光比,分别如图6和图7所示.其中,颜色代表入射光与反射光的功率之比.在NR(图6)和SR(图7)的光谱图中均存在一条明显的色度分界线,分别表示衍射区(右下方)与非衍射区(左上方)的边界和SPR的共振波长.相较于图3可知,NR光谱图中随着入射角度的增加,衍射区延伸到近红外区域,且当TM偏振光入射角大于70◦时,可以在整个可见光范围内实现高效NR效果,见图6(a);TM偏振光在Au和空气的交界面处产生由SPR引起的单峰,只有具有比SPR峰值波长更长的TM光才能被强烈反射,而位于较大入射角处的TE光在可见光和近红外区域主要发生SR,见图7(a)和图7(b).

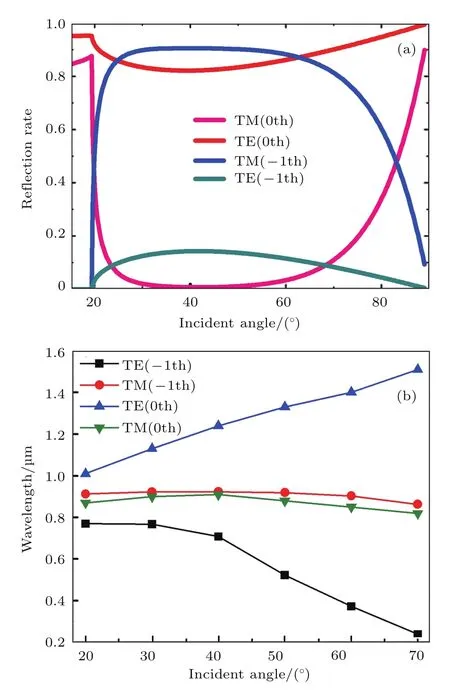
图5 (a)TM和TE偏振光入射时,反射效率与入射角关系曲线;(b)TM和TE偏振光入射时,入射角与反射峰值波长关系曲线Fig.5.(a)Re flection rate versus incident angle curve for TM and TE polarized incident light;(b)wavelengths of light re flection peaks at different incident angles for TM and TE polarized incident light.

例如,选取波长为1µm,入射角为40◦的TE和TM偏振光,NRTM和NRTE的反射效率分别为88%和20%;而SRTE和SRTM的反射效率分别为78%和1%.图6(c)和图7(c)所示为利用两偏振光的反射率之比求得的消光比谱图,可以直接反映反射光的偏振度.在0◦—90◦全角度范围内,NRTM大于NRTE,而在局域范围内SRTE大于SRTM.其中,位于10◦—60◦的入射光内,可以产生200 nm的带宽,其SRTE/SRTM的极端消光倍率比最大可达到106,利用这种性质能够直观地描述金属光栅结构偏振性能的强弱.

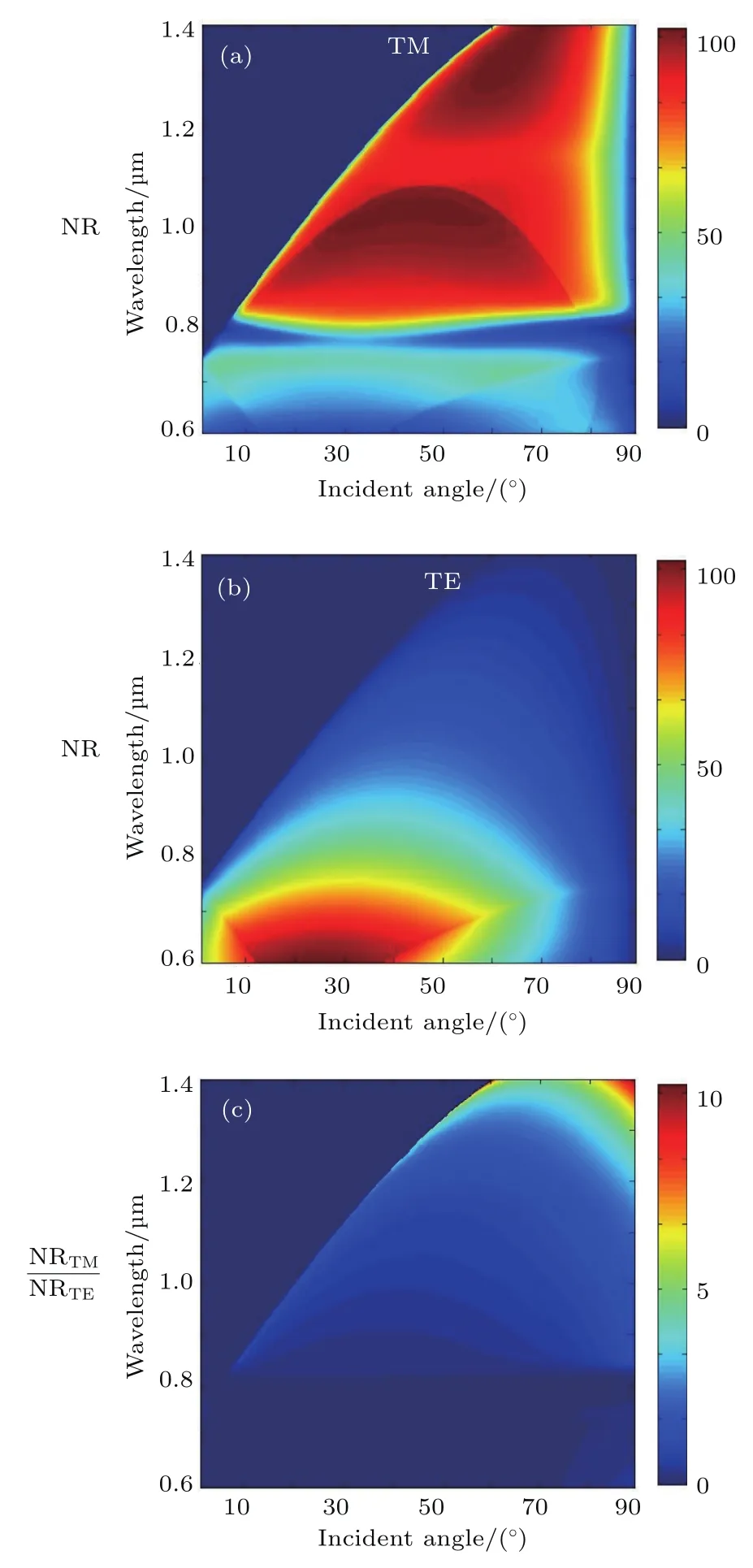
图6 不同偏振光入射时的NR光谱图 (a)TM光入射;(b)TE光入射;(c)消光比Fig.6.NR spectra of different polarized light:(a)TM polarized light;(b)TE polarized light;(c)extinction ratio.

为了进一步验证图4中理想NR点(41.84◦,−41.84◦)所满足的NR和SR的特性,并清晰地再现超表面PBS的分光效果,利用有限元法对16个周期的光栅结构进行了仿真实验,如图8为θ0=41.84◦入射时x-z平面的近场区域分布图.其中,图8(a)所示为TM偏振光入射时y方向的磁场分布图.由图8(a)可知,入射光和NR光在θ0=41.84◦方向的磁场叠加增强,而镜面发射方向θsr=41.84◦的磁场强度极其微弱,因而可忽略不计.图8(b)所示为TE偏振光入射时y方向的电场分布图,SR光与入射光电场强度相等,且关于法线对称.经多次仿真实验发现,随着TM光入射角增大,NR与入射光叠加的磁场强度先增后减,而SR恰恰相反[22−24].

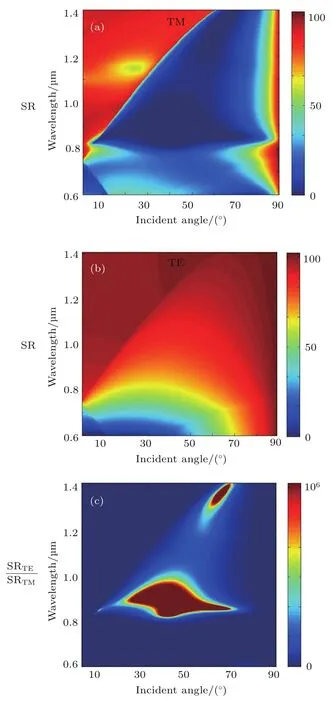
图7 不同偏振光入射时的SR光谱图 (a)TM光入射;(b)TE光入射;(c)消光比Fig.7.SR spectra of different polarized light:(a)TM polarized light;(b)TE polarized light;(c)extinction ratio.

图8 (a)TM光入射(θ0=41.84◦)的磁场模式Hy;(b)TE 光入射(θ0=41.84◦)的电场模式EyFig.8.(a)Magnetic field pattern Hy of TM polarized light(θ0=41.84◦);(b)electric field pattern Ey of TE polarized light(θ0=41.84◦).

4 结 论

本文设计了一种基于金属周期阵列的PBS.对于TM光入射会沿原路反射,且最大NR率大于0.9,当入射角越接近45◦时,NR效果越明显,且在特定情况下可达到理想NR效果,而TE光的NR很弱,并随着波长的增加而急剧下降.本文探讨的金属-介质阵列的截止效应不仅会阻止TE光的透射,还会使得TE光的衍射消失.相比之下,TM光被保留下来,且能产生较为明显的衍射甚至超过狭缝的衍射极限.基于这一现象,高达106的极端消光比的分光器件才得以产生,同时诸多独特的性能特征得以研究和应用.此外,为达到实际所需器件的应用性能,在考虑TE光截止效应的同时,应合理地设置狭缝宽度和光栅周期来确定波长极限;采用合适的狭缝高度,有助于进一步改善反射偏振的消光比.该理论设计结构简单,通过整合衍射、波导和等离子激元效应,成为实用型光束分离装置的理想选择,在全息成像和太阳能电池中具有较好的应用前景.

参考文献

[1]Ebbesen T W,Lezec H J,Ghaemi H F,Thio T,Wol ffP A 1998Nature391 667

[2]Pala R A,Liu J S,Barnard E S,Askarov D,Garnett E C,Fan S,Brongersma M L 2013Nat.Commun.4 2095

[3]Xu T,Wu Y K,Luo X G,Guo L J 2010Nat.Commun.1 59

[4]Monticone F,Estakhri N M,Alu A 2013Phys.Rev.Lett.110 203903

[5]Valentine J,Zhang S,Zentgraf T,Ulin A E,Genov D A,Bartal G,Zhang X 2008Nature455 376

[6]Yu N F,Genevet P,Kats M A,Aieta F,Tetienne J P,Capasso F,Gaburro Z 2011Science334 333

[7]Yin X B,Ye Z L,Rho J,Wang Y,Zhang X 2013Science339 1405

[8]Zhang W G,Zhang Y X,Geng P C,Wang B,Li X L,Wang S,Yan T Y 2017Acta Phys.Sin.66 070704(in Chinese)[张伟刚,张严昕,耿鹏程,王标,李晓兰,王松,严铁毅2017物理学报66 070704]

[9]Jofre M,Anzolin G,Steinlechner F,Oliverio N,Torres J P,Pruneri V,Mitchell M W 2012Opt.Express20 12247

[10]Assemat E,Picozzi A,Jauslin H R,Sugny D 2012J.Opt.Soc.Am.B29 559

[11]Zhang X,Liao Q H,Chen S W,Hu P,Yu T,Liu N H 2011Acta Phys.Sin.60 104205(in Chinese)[张旋, 廖清华,陈淑文,胡萍,于天宝,刘念华 2011物理学报 60 104205]

[12]Luo D,Sun X W,Dai H T,Demir H V 2011Appl.Opt.50 2316

[13]Wang Y P,Wang M P,Huang X Q 2011Opt.Express19 25535

[14]Nguyen H N,Lo Y L,Chen Y B,Yang T Y 2011Appl.Opt.50 415

[15]Wu Y R,Hollowell A E,Zhang C,Guo L J 2013Sci.Rep.3 1194

[16]Chen X,Yang F,Zhang C,Zhou J,Guo L J 2016ACS Nano10 4039

[17]Zheng J,Ye Z C,Sheng Z M,Zhang J 201511th Conference onLasers and Electro-Optics Paci fic RimBusan,South Korea,August 24–28,2015 p1

[18]Ye Z C,Zheng J,Sun S,Guo L D,Shieh H P D 2013IEEE J.Sel.Top.Quant.19 4800205

[19]Ni X J,Emani N K,Kildishev A V,Boltasseva A,Shalaev V M 2012Science335 427

[20]Ordal M A,Long L L,Bell R J,Bell S E,Bell R R,Alexander R W J,Ward C A 1983Appl.Opt.22 1099

[21]Liu M L,Liu R J,Deng X B,Wang Y W,Lei H N 2010Acta Phys.Sin.59 4030(in Chinese)[刘明礼,刘仁杰,邓晓斌,王亚伟,雷海娜2010物理学报59 4030]

[22]Pors A,Albrektsen O,Radko I P,Bozhevolnyi S I 2013Sci.Rep.3 2155

[23]Deng Z L,Zhang S,Wang G P 2016Nanoscale8 1588

[24]Deng Z L,Li X,Wang G P 2017 arXiv:170510171[physics.optics]