马赫-曾德尔干涉仪频谱特性及入射视场展宽技术研究

夏玉宁,王钊,张云,沈法华,2*,仇成群,2*,徐华,2

(1盐城师范学院物理与电子工程学院,江苏省智能光电器件与测控工程研究中心,江苏 盐城 224002;2江苏省大气探测激光雷达技术军民融合创新平台,江苏 盐城 224002)

0 引言

马赫-曾德尔干涉仪(MZI)以分振幅法产生双光束从而实现干涉。与基于多光束干涉原理的法布里-珀罗干涉仪(FPI)相比,MZI干涉频谱的锐度较低,但是也有其独特的优势。首先,在忽略吸收损耗的情况下,MZI能够方便地实现对入射光能的全部利用,光学效率高。其次,它的结构简单,易于通过对其中一个干涉臂调控以实现各种物理量测量。由于传感臂(光程受待测物理量调控的干涉臂)中的光相比参考臂(光程固定干涉臂)中的光产生新的相位差,可以通过观察干涉条纹的移动来确定待测物理量的变化。目前,基于MZI的干涉型传感器已经被广泛应用于温度、压力等物理量测量。此外,MZI便于进行视场展宽,从而放宽对入射光束准直性的要求。由于MZI具有光学效率高、结构简单、便于视场展宽等优势,其不仅在传统的光学通信、传感和检测等领域的应用越来越广泛,而且被作为重要的光学鉴频器之一应用于高光谱分辨率激光雷达和多普勒激光雷达系统中。Bruneau[1,2]于2001和2002年先后提出了基于MZI的边缘技术和条纹成像技术的多普勒激光雷达技术,并于2013年搭建了一套基于MZI的多纵模测风激光雷达系统[3]。Wang等[4-7]对上述技术做了进一步研究,并于2018年研制出了基于光纤MZI的多普勒激光雷达[8]。Hong等[9,10]也对该技术做了理论跟踪研究和视场展宽实验。2015年至2017年,Jin等[11,12]和Ristori等[13]提出了基于可调谐MZI多纵模高光谱分辨率激光雷达技术。2018年至2019年,华灯鑫课题组对该技术做了进一步研究[14,15]。

随着MZI的应用越来越广泛,对其频谱特性的深入研究就显得十分必要。目前一般教科书中仅给出了在理想的单色平行光入射条件下MZI的频谱理论公式。而实际应用中,入射光源是具有一定发散角和谱宽的,这必然会造成MZI的实际频谱特性与理想条件下得到的结果有较大偏差。Bruneau[1]在对MZI频谱特性的理论分析中考虑了入射光谱宽的影响,但没有做深入的定量研究;Hong等[10]将发散角对MZI条纹干涉对比度的影响用附加干涉对比度表示,但没有给出该附加干涉对比度与发散角的定量关系式。因此,为了更好地设计和应用MZI,有必要对此时的MZI实际频谱特性进行深入研究。

本文首先从理论上严格导出了在考虑入射光发散角和谱宽情况下MZI干涉频谱的解析表达式;然后,以干涉条纹对比度为主要评价指标,利用依据解析式编写的软件程序进行仿真并详细分析了入射光发散角和谱宽对MZI干涉频谱的影响;其次,为减小入射光发散角对MZI频谱的影响,深入研究了传统的棱镜式视场展宽技术并分析指出了其在大发散角情况下的补偿效果不佳,提出了依据不同光束发散角选取不同最佳棱镜厚度的视场展宽方法,与传统的棱镜式视场展宽技术相比明显提升了在大发散角情况下的视场补偿效果。

1 理想情况下的MZI干涉频谱函数

如图1所示,假定入射光为理想的单色平行光,忽略反射镜M1、M2以及分束棱镜BS1、BS2的表面缺陷和吸收损耗,并且BS1和BS2的透反比为50/50,则MZI两个通道的干涉频谱可分别表示为

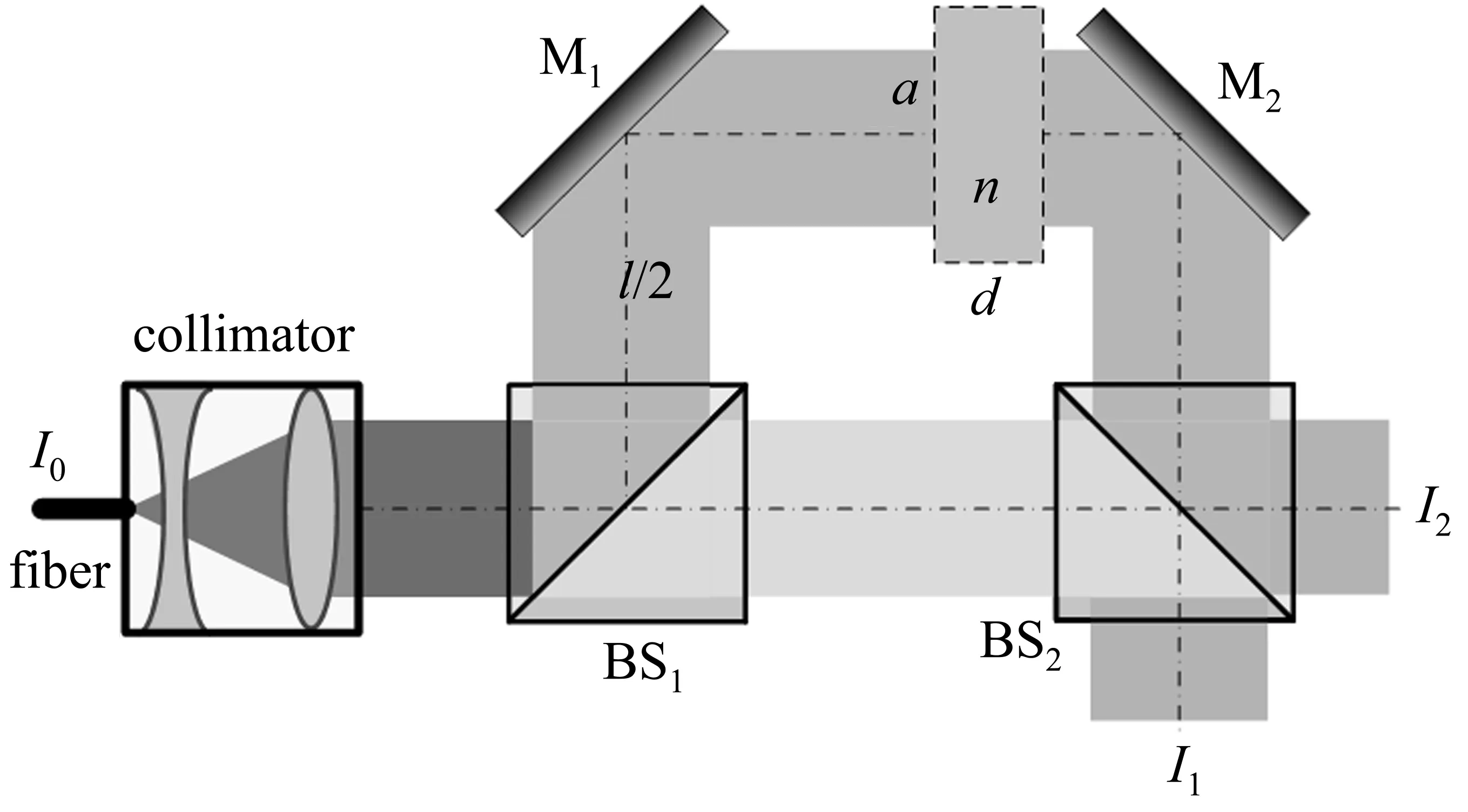
图1 马赫-曾德尔干涉仪双光束干涉原理图Fig.1 Principle diagram of MZI double beam interference

式中:I0、I1和I2分别入射光强、通道1出射光强和通道2出射光强,ν=c/λ为入射光频率,c为真空中光速,λ为入射光波长,l为MZI两干涉臂的光程差。MZI的两个出射通道干涉互补。

2 考虑入射光谱宽和发散角后的MZI干涉频谱函数

2.1 考虑入射光谱宽

在实际应用中,特别是在高光谱分辨激光雷达和多普勒激光雷达应用中,通常采用单纵模激光作为MZI的入射光源(即使采用多纵模激光,其频谱也可等效为多个单纵模激光谱的叠加,下述分析同样有意义),而单纵模激光不是严格的单色光源,有一定谱线宽度。单纵模激光谱通常可近似为高斯分布谱,可表示为

其中:Δνe=Δν/(4ln2)1/2,Δν为入射光谱宽(FWHM)。由此,中心频率为ν的高斯光谱入射MZI后两个出射通道频谱函数为

式中符号“⊗”表示卷积。将(1)～(3)式代入(4)式计算得到

2.2 考虑入射光发散角

在实际应用中,入射至MZI的光束无论是激光器直接发出还是通过光纤耦合等方式得到,都要先经过准直镜准直再进入MZI。然而,经过准直镜准直后的光束仍存在一定的发散角(一般为几至几十mrad),需要考虑其对MZI干涉频谱的影响。假定入射到MZI的光束为光强分布均匀且半发散角为θ0,则MZI的干涉频谱函数为

式中:H1,2(ν,θ)为光束入射角为θ时两个出射通道频谱函数,可由(5)式将l替换为l/cosθ得到。将H1,2(ν,θ)代入 (6)式积分得

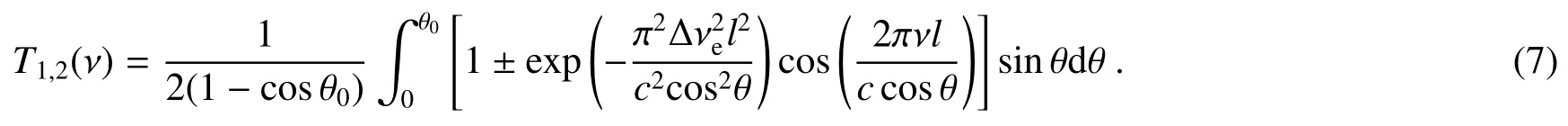
深入分析可以发现由于θ0很小,(7)式中exp指数项可不参与积分,同时有sinθ≈θ和1/cosθ≈1+θ2/2,所以有

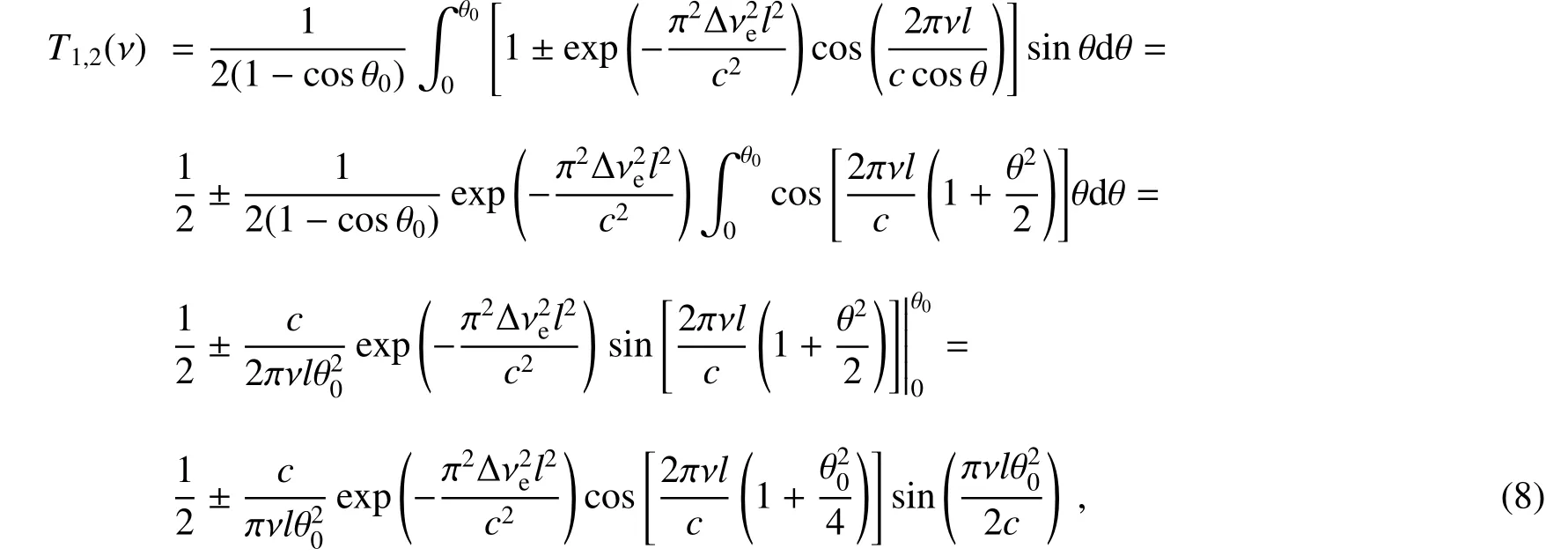
即

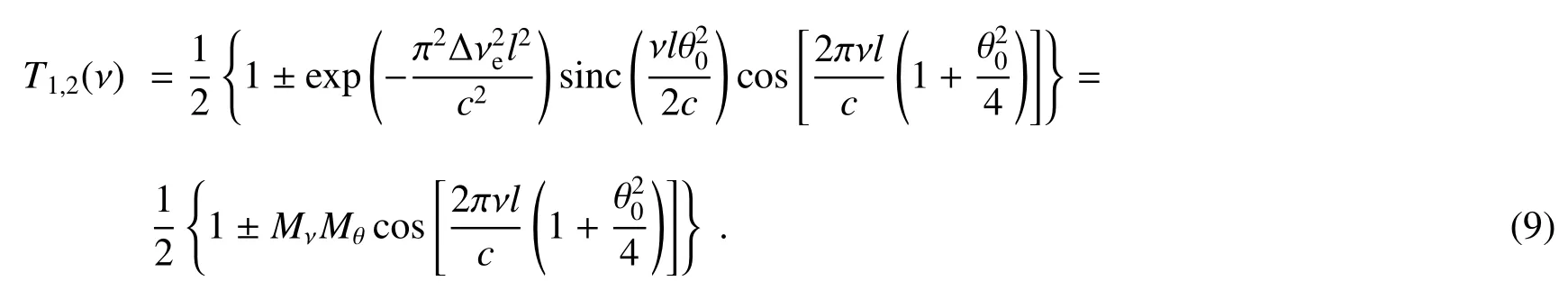
3 入射光谱宽和发散角对MZI干涉频谱的影响分析

为了更好地分析入射光谱宽和发散角对MZI干涉频谱的影响,定义MZI干涉条纹频谱对比度为

此外,为了仿真结果更具参考价值,以文献[1,2]得到的基于MZI分子散射多普勒激光雷达最优参数(λ=355 nm,l=3 cm)和文献[13]给出的基于MZI多纵模高光谱分辨率激光雷达参数(λ=532 nm,l=59 cm)作为两组工作波长和MZI光程差参数值进行仿真,并分别记为(a)组和(b)组。

3.1 入射光谱宽的影响

利用(7)式并假定θ0=0,采用(a)组(λ=355 nm,l=3 cm)参数值得到入射光谱宽分别为0、1、2 GHz的MZI干涉频谱曲线如图2(a)所示;采用(b)组(λ=532 nm,l=59 cm)参数值,得到入射光谱宽分别为0、100、200 MHz的MZI干涉频谱曲线,如图2(b)所示。可以看出:随着入射光谱宽增大,干涉条纹频谱对比度K逐渐减小。此外,由Mν=exp(-π2Δν2el2/c2)可知,光程差l越大,干涉频谱曲线受入射光谱宽增大的影响越明显。图3(a)、(b)分别给出了取(a)组和(b)组参数时,干涉条纹频谱对比度K随入射光谱宽的变化曲线。由图3(a)可见,当入射光谱宽增大至10 GHz时,K将降至2.8%;由图3(b)可见,当入射光谱宽增大至500 MHz时,K将降至3.2%。

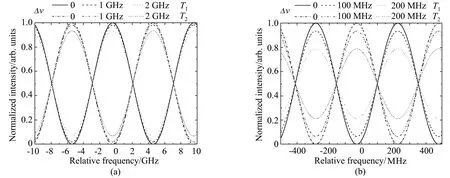
图2 不同光谱宽度入射光的MZI干涉光谱曲线。 (a)θ0=0,λ=355 nm,l=3 cm;(b)θ0=0,λ=532 nm,l=59 cmFig.2 The interference spectrum curve of MZI with different spectral widths of incident light when(a)θ0=0,λ =355 nm and l=3 cm;(b)θ0=0,λ =532 nm and l=59 cm

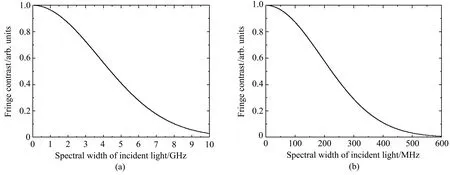
图3 MZI干涉条纹对比度随入射光谱宽度变化曲线。(a)θ0=0,λ=355 nm,l=3 cm;(b)θ0=0,λ=532 nm,l=59 cmFig.3 Variation curve of MZI interference fringe contrast with incident spectral width when(a)θ0=0,λ =355 nm and l=3 cm;(b)θ0=0,λ =532 nm and l=59 cm

3.2 入射光发散角的影响

利用(7)式并假定Δν=0,采用(a)组(λ=355 nm,l=3 cm)参数值,得到入射光半发散角分别为0、2、4 mrad的MZI干涉频谱曲线,如图4(a)所示;采用(b)组(λ=532 nm,l=59 cm)参数值,得到入射光半发散角分别为0、0.5、1 mrad的MZI干涉频谱曲线,如图4(b)所示。可以看出:随着入射光发散角增大,干涉条纹频谱对比度K逐渐减小,同时干涉条纹也逐渐向低频偏移。此外,由Mθ=sinc(lθ20/2λ0)可知,光程差l与λ0的比值越大,干涉频谱曲线受入射光发散角增大的影响越明显。图5(a)、(b)分别给出了取(a)组和(b)组参数时K随入射光半发散角的变化曲线。由图5(a)可见,当入射光半发散角增大至4.5 mrad时,K将降至16.3%;由图5(b)可见,当入射光谱宽增大至1.25 mrad时,K将降至15.0%。同时,从图5(a)、(b)还可以看出,随着入射光半发散角增大,K出现了振荡现象,且振荡幅度越来越小。

图4 不同入射光发散角下的MZI干涉光谱曲线。 (a)Δν=0,λ=355 nm,l=3 cm;(b)Δν=0,λ=532 nm,l=59 cmFig.4 The interference spectrum curve of MZI with different divergence angles of incident light when(a)Δν=0,λ=355 nm and l=3 cm;(b)Δν=0,λ=532 nm and l=59 cm

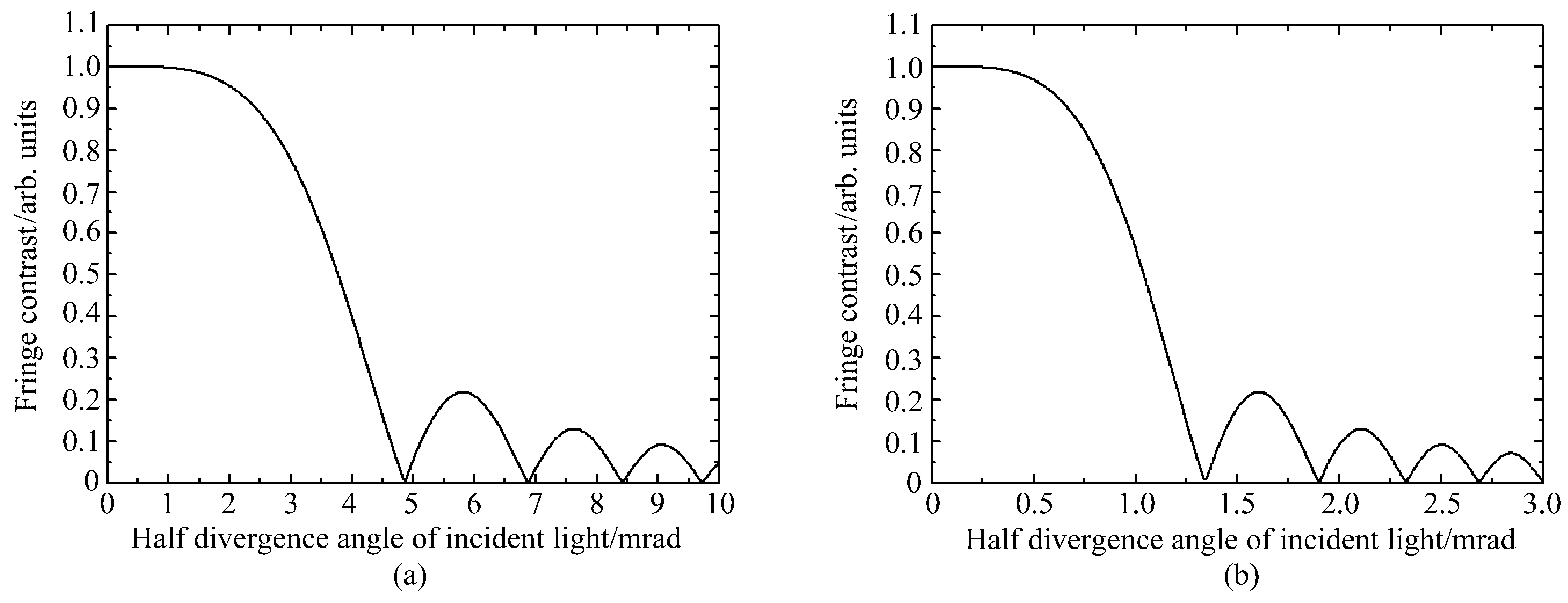
图5 MZI干涉条纹对比度曲线随入射光半发散角变化曲线。(a)Δν=0,λ=355 nm,l=3 cm;(b)Δν=0,λ=532 nm,l=59 cmFig.5 Variation curve of MZI interference fringe contrast with semi divergence angle of incident light when(a)Δν=0,λ=355 nm and l=3 cm;(b)Δν=0,λ=532 nm and l=59 cm

4 视场展宽技术

通过3.2节的分析,可以发现入射光发散角对MZI干涉频谱的影响非常大。为了减小发散角对MZI频谱的影响,需要对MZI进行视场展宽,此处对棱镜式视场展宽技术进行了深入研究。棱镜式视场展宽方案的原理图如图1所示,即在MZI干涉臂中的长臂插入一个折射率为n、厚度为d的补偿棱镜。此时,入射角为θ的光线经过MZI的两个干涉臂后的光程差为

式中:θr为光线进入棱镜后的折射角,有sinθ=nsinθr,因此

由于θ很小,故对(12)式进行泰勒展开得到

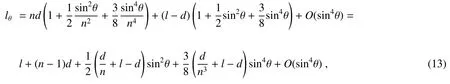
由(13)式可见,忽略sin4θ项及更高阶项,若要lθ与θ无关,需满足d/n+l-d=0,即

此式即为棱镜式视场展宽条件,此时不同θ入射角光线的光程差将相同。若补偿棱镜采用石英玻璃材料,而石英的折射率与波长的关系近似为

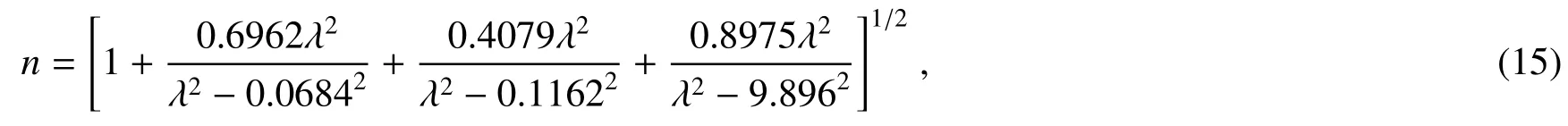
式中波长λ的单位取μm。根据(14)、(15)式,可以求得补偿棱镜厚度d与入射波长λ的关系。图6给出了d与λ的关系曲线,图中假定光程差l=3 cm。

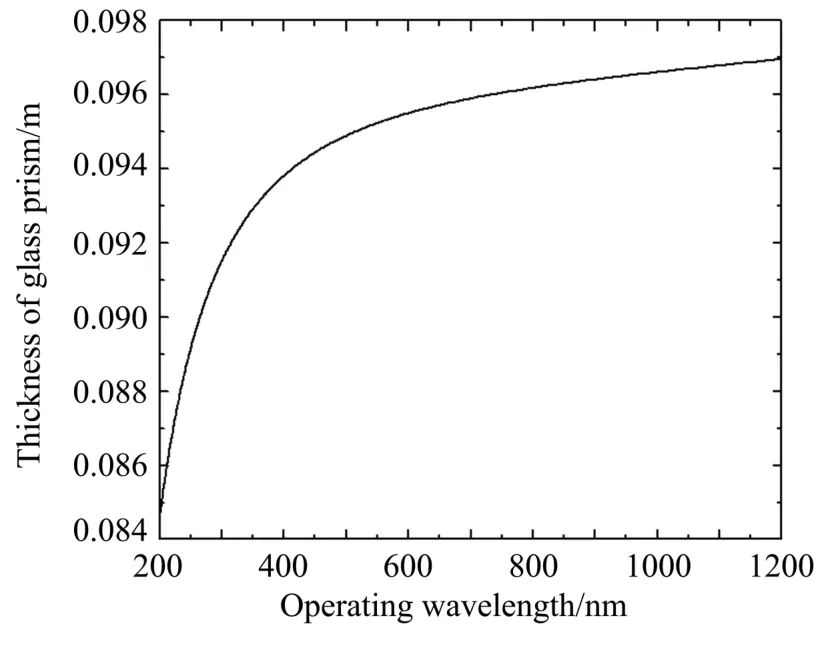
图6 补偿棱镜厚度曲线随工作波长变化曲线Fig.6 Variation curve of compensation prism thickness with operating wavelength

用(12)式lθ表达式替换(5)式中的l,并进一步代入(6)式,得到加入补偿棱镜后MZI两个出射通道干涉频谱函数为

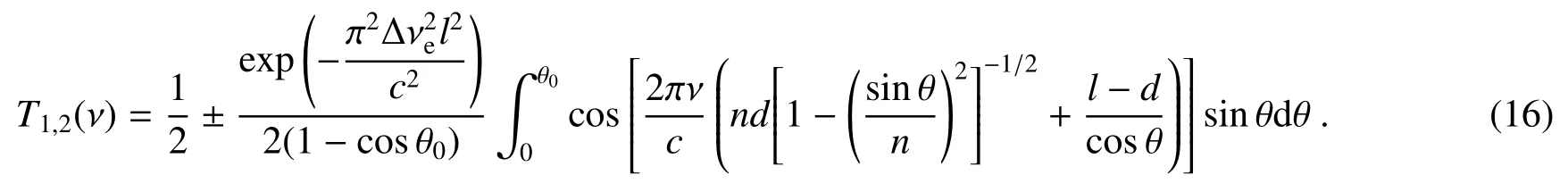
假定补偿棱镜采用石英玻璃材料,采用(a)组(λ=355 nm,l=3 cm)参数值和n=1.4761@355 nm,代入(14)式得补偿棱镜厚度d=0.093 m;采用(b)组(λ=532 nm,l=59 cm)参数值和n=1.4607@532 nm,代入(14)式得补偿棱镜厚度d=1.8707 m(仅为理论分析结果,实际上此厚度的补偿棱镜加工难度很大,可采用高折射率材料或结合使用直角反射棱镜增加穿过棱镜的次数等方法加以实现)。将上述两组参数 (a)组 (λ=355 nm,l=3 cm,n=1.4761,d=0.093 m)和 (b)组(λ=532 nm,l=59 cm,n=1.4607,d=1.8707 m)代入(16)式及(10)式,不考虑入射光谱宽,得到满足(14)式的视场展宽条件时的视场展宽效果曲线分别如图7(a)、(b)所示。由图7(a)可见:取(a)组参数,当入射光半发散角增大至50 mrad时,K仍能保持在93.1%;当入射光半发散角增大至70 mrad时,K将降至33.3%。由图7(b)可见,当取(b)组参数,入射光半发散角增大至25 mrad时,K仍能保持在94.0%;当入射光半发散角增大至35 mrad时,K将降至37.6%。

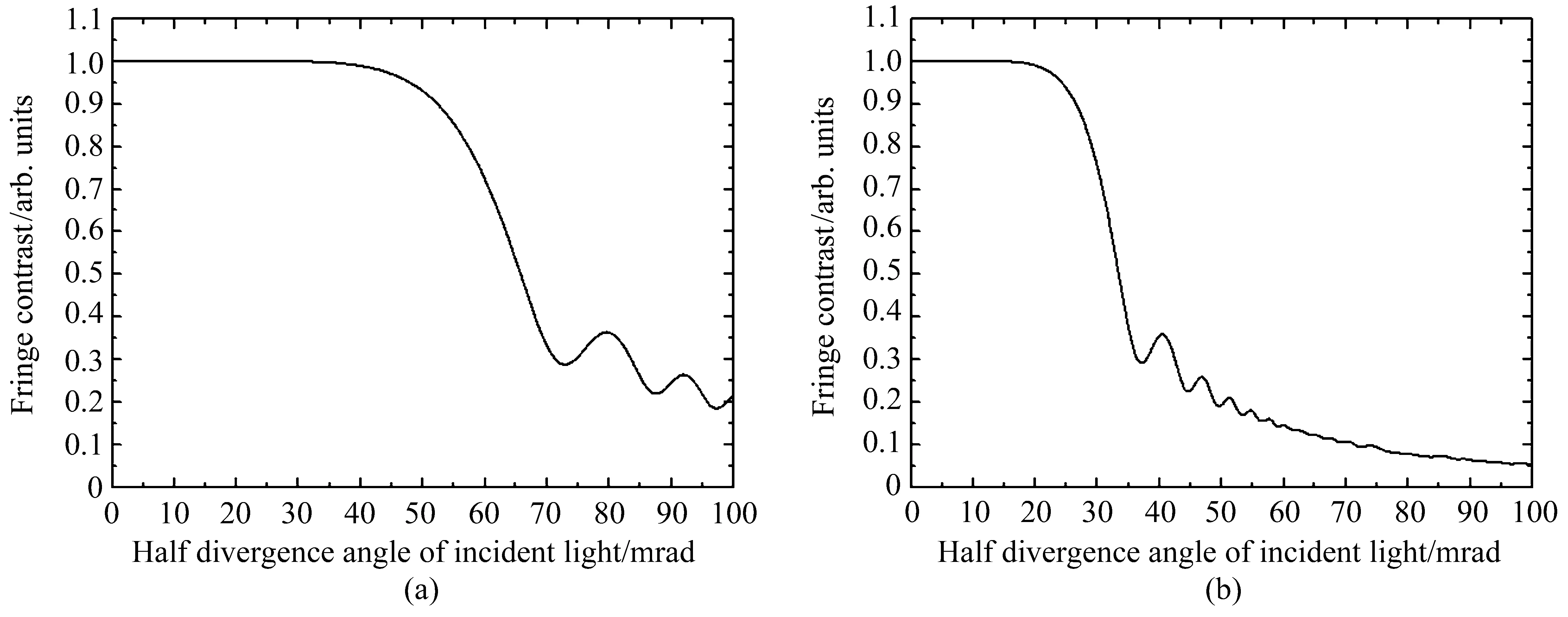
图7 加入场补偿棱镜后,MZI干涉条纹对比度随入射光半发散角变化曲线。(a)Δν=0,λ=355 nm,l=3 cm,n=1.4761,d=0.093 m;(b)Δν=0,λ=532 nm,l=59 cm,n=1.4607,d=1.8707 mFig.7 Variation curve of MZI interference fringe contrast with semi divergence angle of incident light after adding field compensation prism when(a)Δν=0,λ=355 nm,l=3 cm,n=1.4761 and d=0.093 m;(b)Δν=0,λ=532 nm,l=59 cm,n=1.4607 and d=1.8707 m

当发散角较大时,为了更好地实现视场补偿,在(11)式中保留sin4θ项,并令

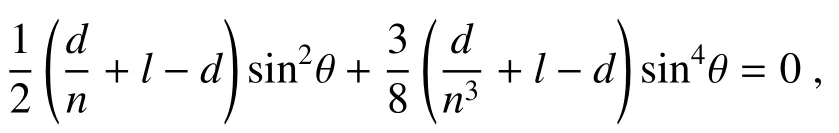
则有

由(17)式可知,补偿棱镜厚度d与θ有关。进一步推理可知,不同的入射光发散角应有不同的最佳d值,而不是(14)式所列的与发散角无关的固定量。

设定入射光半发散角θ0,利用(14)、(8)式,分别代入(a)组(λ=355 nm,l=3 cm,n=1.4761)和(b)组(λ=532 nm,l=59 cm,n=1.4607)参数值,得到K随d的变化曲线分别如图8(a)、(b)所示。由图8(a)可见:取(a)组参数,当θ0分别取50、60、70 mrad时,补偿棱镜的最佳厚度分别为0.09280、0.09272、0.09262 m,此时对应的对比度分别达到了99.4%、97.6%、92.1%,明显优于图7(a)所示结果。由图8(b)可见:取(b)组参数,当θ0分别取25、35、45 mrad时,补偿棱镜的最佳厚度分别为1.8697、1.8687、1.8674 m,此时对应的对比度分别达到了99.6%、94.4%、63.9%,明显优于图7(b)所示结果。

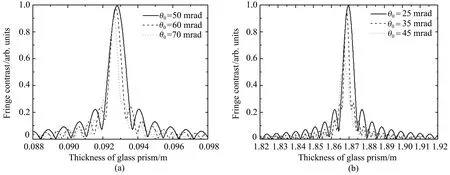
图8 在设定入射光半发散角的情况下,MZI干涉条纹对比度曲线随补偿棱镜的厚度而变化。(a)λ=355 nm,l=3 cm,n=1.4761;(b)λ=532 nm,l=59 cm,n=1.4607Fig.8 Variation curve of MZI interference fringe contrast with the thickness of compensating prism under the condition of setting semi divergence angle of incident light when(a)λ=355 nm,l=3 cm and n=1.4761;(b)λ=532 nm,l=59 cm and n=1.4607

5 结论

研究了有一定发散角和谱宽的光束入射至MZI时的干涉频谱特性。以干涉条纹对比度作为主要的评价指标参数,分别讨论了在入射光波长355 nm、MZI光程差为3 cm(对应分子散射多普勒激光雷达最优参数)和入射光波长532 nm、MZI光程差为59 cm(对应多纵模高光谱分辨率激光雷达参数)两种情形下,入射光发散角和谱宽对MZI干涉频谱的影响。通过分析发现:入射光发散角和谱宽对MZI干涉频谱的影响大小与MZI的光程差有关,光程差越大频谱受入射光谱宽的影响就越显著;光程差与发射光波长的比值越大,频谱受入射光发散角的影响就越显著;很小的入射光发散角(mrad量级)都会对MZI干涉频谱造成很大的影响。由此,进一步研究了棱镜式视场展宽技术。研究表明:在发散角较大的情况下,满足传统的棱镜式视场展宽条件的补偿棱镜不能很好地实现视场展宽;而依据特定发散角选取对应的最佳补偿棱镜厚度的方法则可以更好地实现视场展宽。