浅谈核心素养视角下初中数学课堂教学中的问题设计

■王竞进

数学核心素养是数学课程目标的集中表现，是在数学学习的过程中逐步形成的，在学生自主发展的过程中有着不可替代的作用。核心素养的培养与提升不是另起炉灶，是蕴涵在知识与技能学习过程中的。在初中数学教学过程中，我们要根据内容的特点设计问题，让学生在获得知识的过程中，获得基本数学思想、基本数学活动经验，相应的数学核心素养进而得以提升。笔者就如何提出问题来谈谈自己的做法。

一、问题设计要找准适当的“火候”

在新旧知识转化时、在学生思维发生障碍时、在学生产生疑惑时、在学生思考关键处等，教师提问应设计得恰如其分。如在教授苏科版《数学》八年级上册第六章“探究一次函数的图像”时，课堂上有的学生可能会问“为什么一次函数的图像是一条直线”，这是一个非常有意义的话题。此时，有的学生会通过列表、描点、连线等过程画出函数图像，通过观察、发现一次函数的图像是一条直线；有的学生会根据函数表达式中变化的量相同，得出它的图像应该是一条直线而不是折线。笔者听课发现，课堂上解决这样的问题，往往就会被学生的观察、操作等活动一划而过，得出函数图像的性质，这样的学习是缺乏深度的学习。当学生找不到突破口时，教师应在知识形成过程的“关键点”上提出问题：要证明几个点在同一直线上，应该先说明其中的几个点在同一直线上？要证明三点共线的问题，往往可以通过怎样的方法解答呢？

在面对一般问题无从下手时，引导学生考虑特殊化解决，以认识问题本质，积累解决问题的经验。从数学学习、研究过程来看，通过类比、推广、特殊化等，可以促进数学思考，可以有效地寻找自己感兴趣的问题，从中获得研究方法的启示，提升逻辑推理的能力。

二、问题设计要有精心的预设

笔者在苏科版《数学》八年级下册“分式的基本性质”第一课时的导入中，设计了这样的问题：分数相等吗？等式从左到右是如何变形的？由等式，你还能够写出相等的等式吗？你能用含a的式子表示这个等式吗？那么与分式相等吗？分式也有类似的性质吗？通过对上节课学习分式概念过程的回忆，以及对小学分数约分的回顾，让学生复习分数的基本性质，引导学生应用分数基本性质时，特别要注意分数的分子与分母同时乘（或除以）的这个数，必须是不能为0的数，为后续类比、探索分式的基本性质做铺垫。在学生复习分数基本性质的基础上，让学生“写出与相等的等式”，这样的结果有无数个，大胆猜想，将分数的分子、分母中的数转化为用含有字母的代数式，类比地提出分式具有的性质。在经历从特殊到一般、从具体到猜想的过程中，激发了学生探求新知的欲望，让学生初步感受分式的基本性质。这样的活动过程是建立在学生认识分数基本性质的基础上，对于分式的基本性质需要有不完全归纳的体验过程。因此，在教学过程中，仅仅告诉学生“也有类似的性质”是不够的，对于问题的设计要精心预设，知识的生成才能自然、水到渠成。

三、问题设计要有思考的深度

问题设计应在学生的“最近发展区”，帮助学生发现本质，解决难点。教师要根据知识难度、思维跨度等，综合确定问题解决需要的“能量”。如：已知关于x的一元二次方程mx2+2x-1=0有两个不相等的实数根，则m的取值范围是______。本题是对一元二次方程根的判别式的直接应用。实际上面对这样的问题，学生还是停留在记忆层面上。教师应强化“有两个不相等的实数根”的条件。学生还没有具体问题情境可结合，对一元二次方程根的判别式缺乏明晰的认识。教师不妨将问题变形为已知关于x的方程mx2+2x-1=0有实数根，则m的取值范围是_______。

四、问题设计要有不同的梯度

问题设计要有层次性，需要从知识的角度步步深入、从思维的角度由浅入深、从问题解决的角度进行发现、提出与解决等，学生不断面对新的合适的挑战，引导一节课有序推进。在苏科版《数学》八年级下册对“图形的旋转性质”进行课堂训练时，笔者设计了如下3道题：

问题1：如图1，将Rt△ABC绕直角顶点C顺时针旋转 90°，得到△A′B′C，连接 AA′，若∠1=25°，则∠BAA′的度数是（ ）。

A．55° B．60° C．65° D．70°

问题2：如图2，将△ABC绕点A逆时针旋转100°，得到△ADE。若点D在线段BC的延长线上，则∠B的大小为_____。

问题 3：如图 3，在正方形网格中，线段A′B′是线段AB绕某点逆时针旋转角α得到的，点A′与A对应，则角α的大小为（ ）。

A．30° B．60°

C．90° D．120°

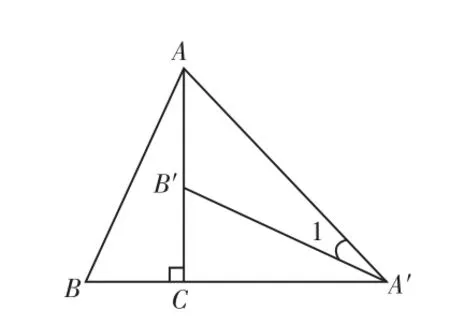
图1

笔者在上面问题的阶梯式设置中，能够尽可能满足不同层次学生的学习需要，充分凸显了解、理解运用、综合分析三个层次。第1问属于第一阶梯，面向基础组的学生，问题主要是基本的概念和浅显的问题，强调图形旋转概念的基本知识和方法的一般性运用，重在学会模仿；第2问属于第二阶梯，主要面向中层组的学生，问题为具有发展性的和稍有变化的，以教授基础知识和训练基本技能为重点，培养其一般的数学思维，重在理解图形旋转的性质；第3问属于第三阶梯，主要面向能力发展、提升组的学生，问题的设计具有一定的综合性和能力性，重在培养其思维的严谨和广阔，发展其抽象思维和灵活运用知识的能力。这样的问题设计，层层衔接，步步为营，逐步递进，每一阶梯的问题不仅能够针对不同层组的学生，而且使得前面的问题也作为后面问题解决的基础，为不同层次学生独立完成分层目标。

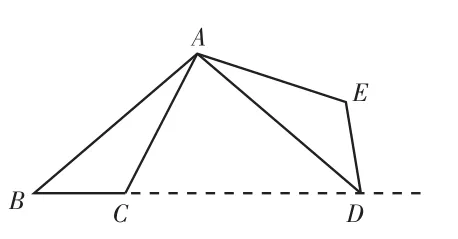
图2

图3

五、问题设计要有多维的角度

问题的指向性需明确，要不断引导学生发现问题的本质，多角度地思考问题，加强知识间的纵横联系，提高学生分析问题、解决问题的能力。如：如图4，在正方形ABCD中，点P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于点F。

（1）证明：PC=PE；

（2）求∠CPE的度数；

（3）如图5，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°，连接CE，试探究线段AP与线段CE的数量关系，并说明理由。

图4

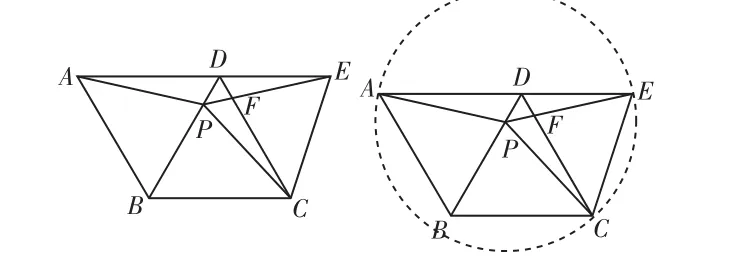
图5

这类问题主要是一种策略性的引导，可以应用三角形的全等条件、性质，正方形、菱形的性质以及三角形的内角和知识进行解答，还可以根据条件中隐含着点A、E、C到点P的距离相等，构造以点P为圆心、AP为半径的圆，将所求角转化为圆的圆心角。通过这样多角度地思考问题，有利于培养和发展学生的求异思维、发散思维、逆向思维等进行创新活动所必需的思维形式。在我们的数学课堂当中必须把一切能给学生的机会都给学生，对于新的知识点，要大胆放手让学生自己思考，自主探究、比较、发现，让学生学会从多角度思考问题，提高课堂教学的有效性。

六、问题串设计要有关联度

一节课中的问题设计，需要逻辑严密、前后呼应，通常以问题串的形式出现。一组问题组成一个完整的问题串，能够激发思考，启迪思维，引导学生把握数学内容的本质。设计探索型问题串，需要围绕定理、法则和公式的发生、形成、发展三个过程逐步展开，不断引导学生观察、动手操作、比较分析、猜想归纳，在“做数学”中学数学，获得数学学习的体验，提高探索能力，体味到数学的无穷魅力，以此促进学生的数学学习。再如教授苏科版《数学》七年级下册“认识三角形”中的三边关系时，笔者是这样设计的：

准备：4根小木棒，长分别为3、5、7、10(cm)。

（1）用手中的木棒摆一摆能摆成几个不同的三角形？并把边长记下来（其中最短边记作a，较短边记作b，最长边记作c）。思考是否任意长度的三根木棒都能围成三角形？

（2）计算并比较：

a+b___c；b+c____a；c+a___b；

a-b____c；b-c____a；c-a____b。

（3）通过以上计算，你认为三角形的三边存在怎样的关系？

（4）三角形三边关系的依据是什么？

（5）判断下列各组线段中，哪些能组成三角形，哪些不能组成三角形，并说明理由。①a=2.5cm，b=3cm，c=5cm。②e=6.3cm，f=6.3cm，g=12.6cm。追问：在三条线段长度都已给出的前提下，如何更好地运用性质？

问题（1）“摆一摆”活动让学生积极性高涨，进一步的追问把学生从单纯的动手操作引向有意义的思考。问题（2）使学生的探究更具体、明确。问题（3）鼓励学生比较分析、大胆归纳。问题（4）说明从实验中的特殊数据得出结论不一定可靠，需要严格的逻辑证明，使结论一般化，培养学生严谨的治学态度。问题（5）巩固和运用性质，“追问”使性质得以发展。5个问题可操作性强，以“为什么探究边性质→怎么探究→结论是什么→依据是什么→结论的推论是什么”为主线步步深入，紧紧围绕性质的发生、形成、发展进行设计，融合成一个整体。学生在此过程中充分参与合作探究，真正体验“做数学”的乐趣。