带式输送机驱动滚筒的有限元分析与结构优化

刘宝林，孟文俊，邬思敏，杨伟杰

(太原科技大学 机械工程学院，太原 030024)

H带式输送机是高效的散状物料连续输送装备，广泛应用于矿山、煤炭、建材、化工、港口、粮食、电力等行业部门。近年来，通过引进国外先进带式输送机设备及其技术，以及国内学者和科研技术人员的共同努力，国内长距离、大运量、高带速的带式输送机的设计和制造水平取得很大发展。

目前带式输送机驱动滚筒的设计方面，还缺乏系统、完善和精确的设计方法[1-2]。许多生产部门遵循设计手册直接选用，手册中给出的推荐选型是通用型号，而且其结构尺寸安全余量很大。一些厂家根据生产制造经验以及实际工程应用情况，对驱动滚筒结构进行优化，优化效果明显。但依然缺乏相关理论支持和有效的设计方法。随着现代设计理论和方法的快速发展，以及绿色环保和低碳节能要求的提高，高可靠性和轻量化制造倍受关注。

对带式输送机驱动滚筒受力分析研究，基于有限元分析方法，通过微粒群智能算法对驱动滚筒结构尺寸优化，并采用APDL/VB混合编程，编制驱动滚筒优化设计软件。

1 驱动滚筒受力分析及有限元模型加载

1.1 确定驱动滚筒载荷形式

驱动滚筒是带式输送机工作的关键核心部件，其能否安全可靠的运转是整个带式输送机的关键。

带式输送机驱动滚筒工作时受到载荷十分复杂[2]，其主要载荷有两种：径向压力载荷和周向摩擦力载荷。

缠绕在驱动滚筒上的输送带，其张力沿绕出点2到绕入点1的方向呈指数函数分布逐渐增加，因而驱动滚筒的径向压力载荷也呈周向指数分布，如图1所示，且输送带张力变化符合欧拉公式：

S1=S2eμα

(1)

式(1)中：S1——输送带绕入点1处张力，N；

S2——输送带绕出点2处张力，N；

μ——驱动滚筒与输送带间摩擦系数；

α——驱动滚筒利用弧，rad.

图1 驱动滚筒张力示意图
Fig.1 Tension force of driving drum

而驱动滚筒的轴向载荷分布目前有两种描述：即呈线性均匀分布载荷和呈非线性半正弦函数分布载荷，而非线性半正弦函数分布压力能更加准确描述驱动滚筒轴向实际受力分布[3]。其载荷沿驱动滚筒轴向分布函数曲线如图2所示。

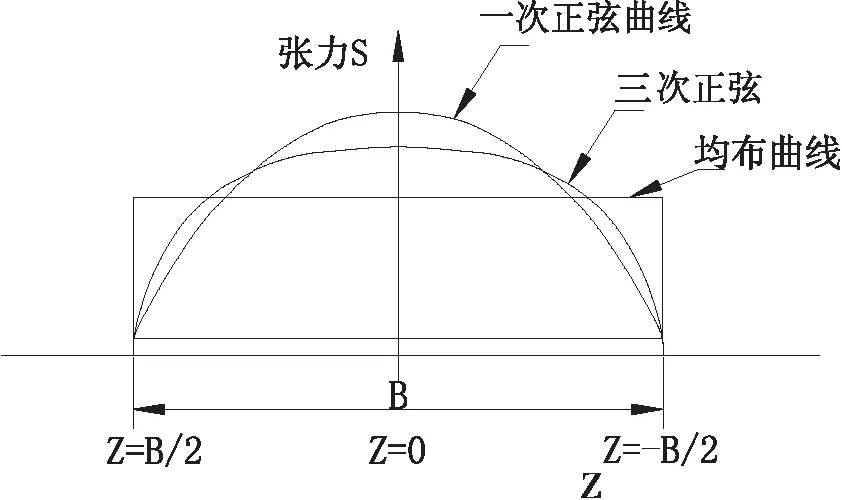
图2 载荷分布函数曲线示意图
Fig.2 Schematic diagram of load distribution curve

采用一次半正弦函数曲线分布力加载，结合欧拉公式可得到驱动滚筒受载面内任一位置单位表面正压力计算公式[4]如下：

(2)

式(2)中：P——驱动滚筒表面计算压力，N；

B——输送带带宽，m；

D——驱动滚筒直径，m；

z——轴向位置，m.

同时由式(2)可以得出驱动滚筒该位置受到输送带的周向摩擦力计算公式为：

(3)

1.2 建立有限元模型及仿真计算

采用APDL参数化语言对ANSYS进行二次开发，编写驱动滚筒有限元仿真专用程序，实现对系列化驱动滚筒的有限元仿真。以便与VB混合编程，结合微粒群算法优化计算。

驱动滚筒是复杂的装配组合体，适当地简化有限元分析模型，可以在保证一定计算精确度前提下减少仿真计算量，提高仿真效率。本文对滚筒进行以下简化：(1)忽略轴承座，简化为对轴的圆周约束，本文主要研究驱动滚筒受力和变形，省略胀套的拧紧螺钉、轴节和销孔等次要元素；(2)鼓形滚筒简化为柱面滚筒，用非线性半正弦函数分布载荷加载模拟；(3)忽略筒体焊缝，其余焊缝在建模中GLUE命令粘接处理，虽然轮辐和筒体之间的焊缝存在内应力，但其对整个滚筒的强度影响不大；(4)忽略滚筒表面包胶，胶面的主要失效形式是磨损和老化，不在本文研究范围之内。

建模过程：APDL命令流生成点、线、面，绘出滚筒轴向截面；用VROTAT命令将绘制的截面旋转成体；建立分割面，用VSBA命令分割筒皮、轮毂、轴等，分别赋予相应材料属性并划分网格。

模型加载：轴上轴承部位添加位移约束，设置为简支梁形式约束[4]。在筒面加载位置设置表面效应单元，按载荷分布形式逐个单元加载径向载荷和周向载荷。采用4节点表面效应单元，分别取出单元的4个节点的三坐标值，计算各个节点的径向压力P1，P2，P3，P4，将其平均值P加载到单元上。ANSYS中有限元模型实际加载效果如图3，4.

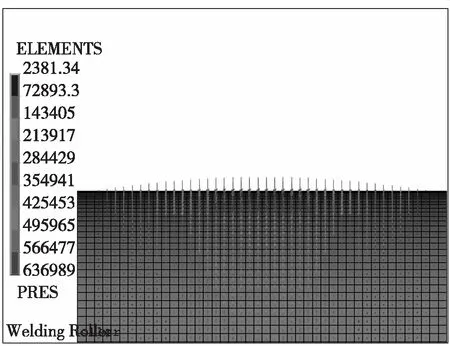
图3 有限元模型网格与轴向加载
Fig.3 Finite element model and axial load

如图5，图6中仿真结果可以看出，驱动滚筒的最大位移出现在筒皮上对应输送带绕入点的位置，最大应力出现在轴承支撑面上，胀套位置也是筒体应力最大位置，这与驱动滚筒实际破坏形式相吻合，仿真数据准确可靠。对应该驱动滚筒，最大应力为120 MPa，最大应变为1.04 mm.驱动滚筒轴采用40 Cr，工作中最大应力小于其许用应力，最大应变为弹性应变，且在允许范围内，驱动滚筒安全可靠。

图4 有限元模型的周向加载
Fig.4 Circumferential load of finite element

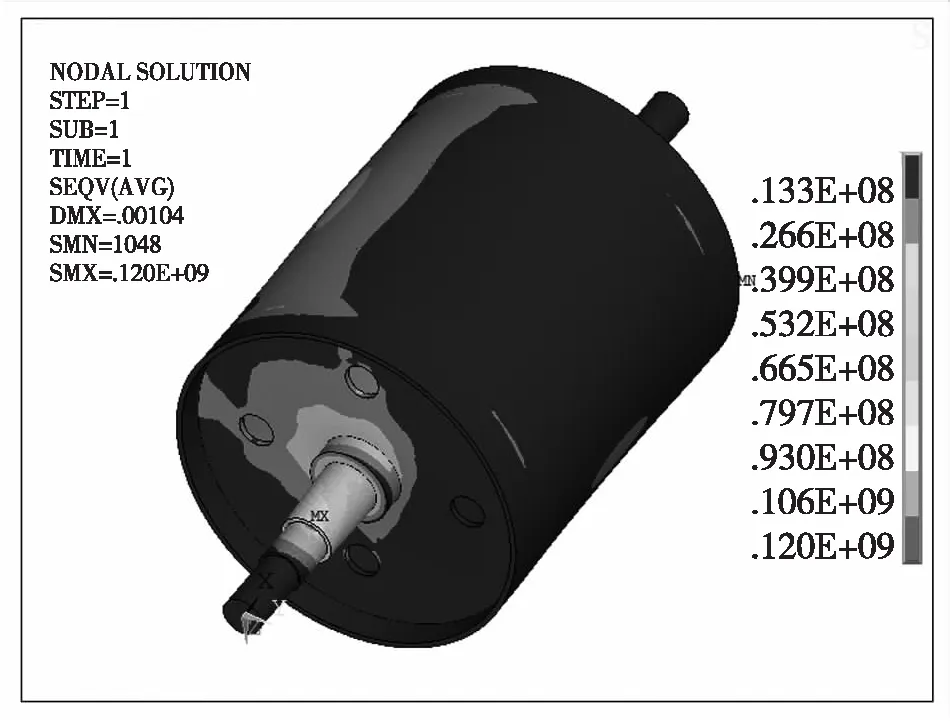
图5 应力等值线图
Fig.5 Stress contour map

图6 应变等值线图
Fig.6 Strain contour map

2 基于有限元分析的微粒群优化设计软件

2.1 驱动滚筒的微粒群优化算法

微粒群算法(Particle Swarm Optimization, PSO)是随机优化算法的一种，于1995年由J.Kennedy和R.C.Eberhart等提出，经过国内外诸多学者的研究和探索，微粒群算法得到长足的发展。其发展目前主要集中在惯性权重和学习因子的控制策略，及其与其他智能算法的混合变异的研究[5]。微粒群算法具有结构简单，参数少，使用方便，算法中无需梯度信息，对问题的依赖小等特点，在连续函数优化问题和离散函数优化问题的优化效果明显。

微粒群算法是一种群体智能算法，一种模拟鸟类觅食这一社会性生物行为的启发式算法。微粒群初代颗粒在随机初始化后，受个体智慧与群体经验影响，经过多次调整迭代达到最优位置。

本文采用Shi和Eberhart提出的标准微粒群算法，选择合适的惯性权重和学习因子控制策略[6-9]。标准算法颗粒速度更新公式为：

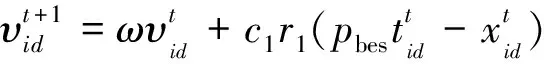
(4)

式(4)中：ω——惯性权重，影响算法的搜索能力；

r1,r2——均匀分布在区间(0,1)的随机数；

c1,c2——颗粒学习因子；

颗粒位置更新公式为：

(5)

优化设计变量[9-12]：x=[x1,x2,x3,x4]，分别为驱动滚筒筒皮厚度x1，辐板厚度x2，辐板距离x3，轴径x4.

优化约束条件：依据有限元分析结果，应力/应变不得超出驱动滚筒安全运行允许范围。以及实际生产中，选用原材料确定的设计变量x的取值范围。

优化目标函数(颗粒适应度)：驱动滚筒的总质量。驱动滚筒由不同材料的零部件焊接装配而成，算法中分别计算各零部件体积，求得驱动滚筒的总质量。

2.2 编制驱动滚筒优化设计软件

通过APDL/VB混合编程的方式编制软件，将有限元分析与微粒群算法结合起来对带式输送机驱动滚筒优化设计[10-15]。优化设计软件中算法的具体实现步骤如下：

①初始化。设定PSO算法各项参数，并根据设定的设计变量范围初始化颗粒。

②生成APDL文件。将颗粒位置参数赋予对应的驱动滚筒的结构尺寸，生成APDL命令流文件。BATCH模式调用ANSYS有限元软件计算，分析结果提取最大应力/应变，保存到TXT文件，以备使用作为优化约束条件。

③计算适应度值。计算各个粒子的适应度值，符合约束的颗粒中找出当代最优颗粒，并更新颗粒历史最优位置和颗粒群全局最优位置。

④检验是否结束迭代。若符合迭代结束条件转到⑥，否则转到⑤.

⑤更新颗粒。根据微粒群算法的速度更新公式(4)和颗粒位置更新公式(5)，更新颗粒速度和位置，转到②继续运算。

⑥优化结束并输出优化结果。

基于APDL有限元分析的微粒群优化设计软件流程图如图7.

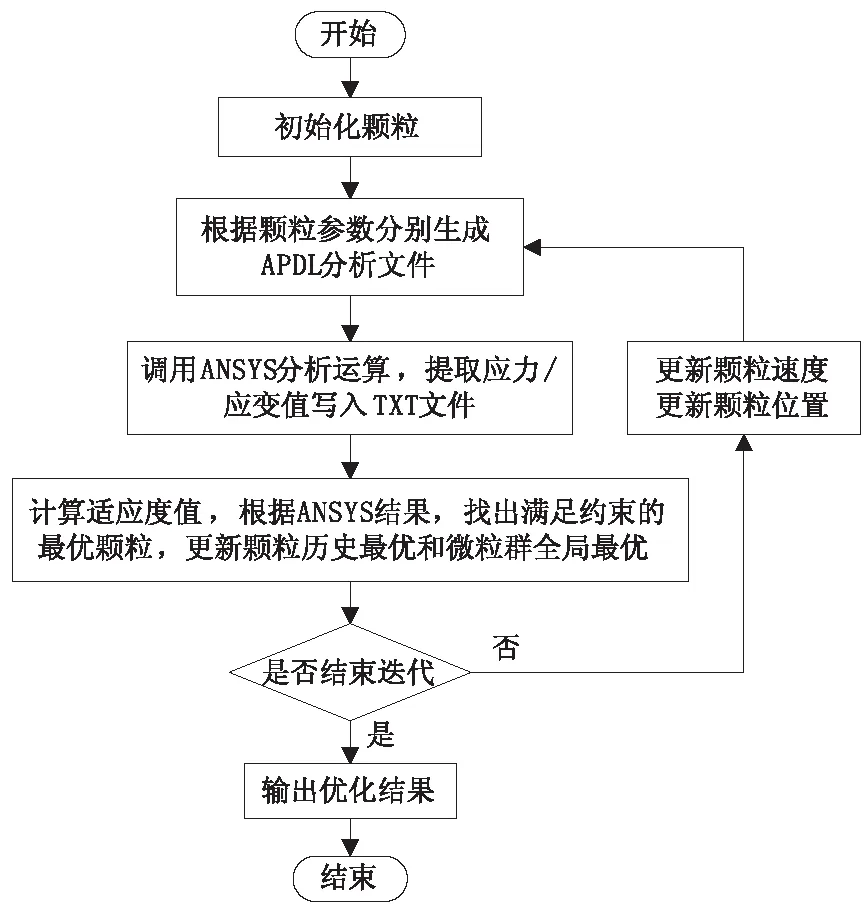
图7 优化算法流程图
Fig.7 Optimization algorithm flow chart

优化设计软件的编制及流程控制主要在VB平台中实现，优化设计软件与ANSYS有限元分析软件的参数与数据交换如图8.主要为：①微粒群优化软件，将颗粒位置参数分别赋给对应的滚筒结构尺寸参数，并生成APDL命令流文件。② ANSYS软件BATCH模式读取APDL命令流文件进行有限元分析计算，分析结果中提取应力/应变值写入TXT文件。③微粒群优化软件读取TXT文件判别对应颗粒是否满足应力/应变约束要求。

图8 参数/数据交换
Fig.8 Parameters/Data exchange map

3 算例及优化结果分析

以某带式输送机为例，通过采用上述方法编制的优化设计软件进行设计计算。输送机参数如表1所示，驱动滚筒各零部件材料参数如表2.且输送机平稳运行时，驱动滚筒上绕出点输送带张力为：

S2=202 594.3 N

(6)

表1 输送机参数表
Tab.1 Conveyor parameters

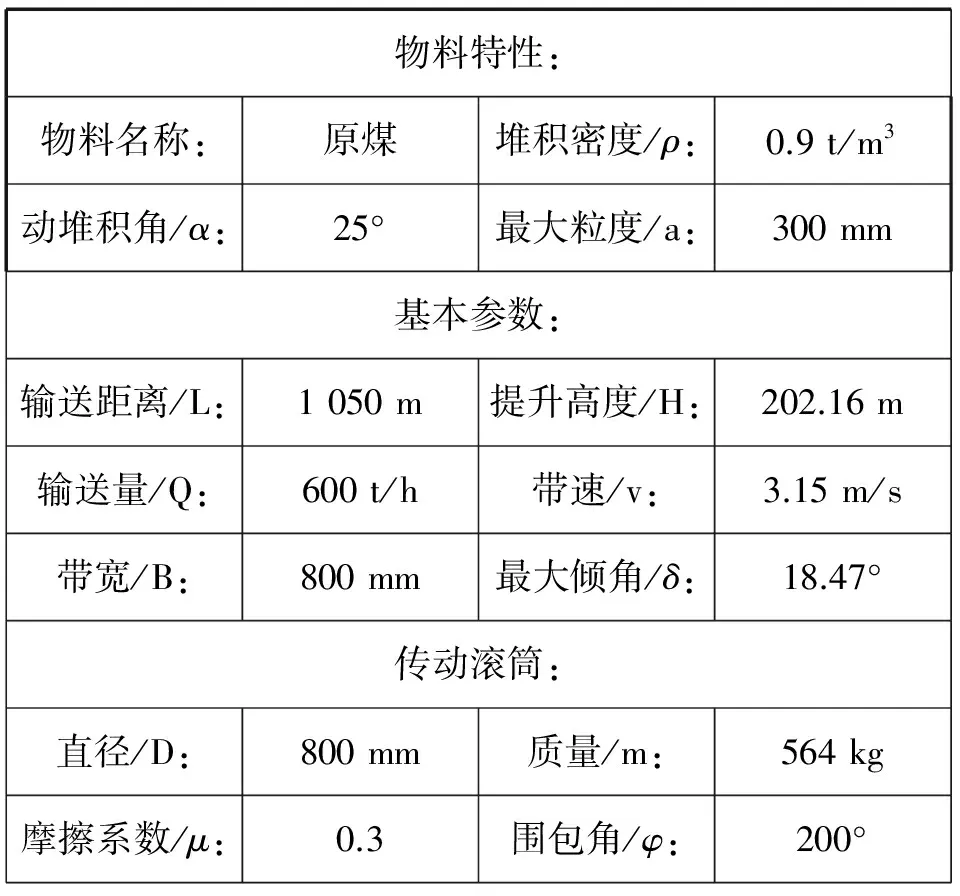
物料特性：物料名称：原煤堆积密度/ρ：0．9t/m3动堆积角/α：25°最大粒度/a：300mm基本参数：输送距离/L：1050m提升高度/H：202．16m输送量/Q：600t/h带速/v：3．15m/s带宽/B：800mm最大倾角/δ：18．47°传动滚筒：直径/D：800mm质量/m：564kg摩擦系数/μ：0．3围包角/φ：200°

表2 驱动滚筒各部件材料属性
Tab.2 Material properties of each part

构件名称材料弹性模量/Pa泊松比密度/Kg·m-3筒壳Q2352E110．287850轮辐/轮毂2G230⁃4502．07E110．287800轴40Cr2．07E110．34500

在软件中输入必要的驱动滚筒结构尺寸，设置设计变量的范围、最大迭代次数和迭代结束条件，进行优化运算。优化结果绘制折线图如图9所示。

图9 优化迭代折线图
Fig.9 The line chart of optimization iteration

该算法前期搜索能力强，后期有一定的收敛速度。优化后驱动滚筒参数为x=[8,10,800,125]，总质量为422.46 kg，相比优化前减重25%左右，优化效果显著。

如表3中，为驱动滚筒优化前、ANSYS软件中一阶搜索优化结果以及本文中方法优化结果的参数对比。其中ANSYS中Design OPT优化求解器采用零阶优化方法，优化后相比优化前减重约20%，本文中方法(APDL/PSO)优化后减重约25%.基于有限元分析的微粒群优化方法有更好的优化效果，更接近驱动滚筒的真实最优结构尺寸。

通过结合有限元分析理论和微粒群优化方法对带式输送机驱动滚筒优化设计，在保证安全和高可靠性的前提下，达到轻量化设计制造。符合现代绿色环保和节能高效的生产要求。本算法为驱动滚筒的优化设计提供方法依据，对其轻量化设计与制造有一定的指导意义。

表3 驱动滚筒优化前/后参数表
Tab.3 Parameters of driving drum before/after optimization

驱动滚筒参数优化前DesignOPTAPDL/PSO筒皮厚度/mm1288辐板厚度/mm141210辐板距离/mm800800800滚筒轴径/mm130127125滚筒质量/kg563446422最大应力/MPa97．2697．3196．89最大应变/mm0．410．560．58

4 结 论

有限元分析部分采用APDL参数化建模、网格划分、求解运算、提取结果数据，建模准确，加载合理，具有较高的仿真精度。优化设计软件中微粒群智能算法，前期搜索能力强，后期也有较快的收敛速度。

基于有限元分析的微粒群优化设计软件优化精度比较高，但是运算过程中颗粒多、迭代次数大，因而优化计算量大，比较费时，对计算机性能的要求极高。设计生产中需要权衡利弊，而且本优化方法基于有限元仿真，有待实验验证和工程检验。

参考文献：

[1] 刘铁钢.传动滚筒筒体结构有限元分析[D].大连:大连理工大学,2014.

[2] 胡瑾.带式输送机滚筒的结构优化与再制造[D].太原：太原科技大学,2015.

[3] 李峰,崔志远,韩刚.基于ANSYS的传动滚筒的有限元分析[J].太原科技大学学报,2007,28(4):307-310.

[4] 关维娟.基于遗传算法的带式输送机滚筒优化及其虚拟设计[D].合肥：安徽理工大学,2009.

[5] WANG L, KANG Q, XIAO H, et al.A modified adaptive particle swarm optimization algorithm[C]// IEEE International Conference on Industrial Technology.2012:209-214.

[6] 胡建秀, 曾建潮.微粒群算法中惯性权重的调整策略[J].计算机工程, 2007, 33(11):193-195.

[7] KIRANYAZ S, INCE T, YILDIRIM A, et al.Fractional particle swarm optimization in multidimensional search space[J].A Publication of the IEEE Systems Man & Cybernetics Society, 2009, 40(2):298-319.

[8] CHEN W N, ZHANG J, CHUNG H S H, et al.A novel set-based particle swarm optimization method for discrete optimization problems[J].IEEE Transactions on Evolutionary Computation, 2010, 14(2):278-300.

[9] WEI Z, SHI Y, MA D, ET AL.Modified Particle Swarm Optimization algorithm by enhancing search ability of global optimal particle[C]// IEEE International Conference on Electronic Measurement & Instruments.2015.

[10] 周金莲.基于改进粒子群算法的带式输送机滚筒的优化设计[J].煤矿机械,2013,10:18-20.

[11] 乔李宁.基于ANSYS的带式输送机滚筒优化设计[J].煤矿机电,2009(4):87-89.

[12] 赵义.基于ANSYS的带式输送机传动滚筒的有限元分析及优化设计[D].石家庄：河北工程大学,2013.

[13] 曾建潮.微粒群算法[M].北京：科学出版社, 2004.

[14] 李丽, 牛奔.粒子群优化算法[M].北京：冶金工业出版社, 2009.

[15] ZHANG Z, JIA L, QIN Y.Modified constriction particle swarm optimization algorithm[J].系统工程与电子技术：英文版， 2015, 26(5):1107-1113.