发现学习：促进初中生数学学科核心素养提升的有效途径

赵春风

[摘 要] 核心素养是教学目标，教学目标的实现需要具体途径. 初中数学学科核心素养的培育，可以经由发现学习来实现. 理论上，发现学习所需要的心智付出是面向核心素养的关键能力的；实践中，两者是吻合的，因此发现学习是核心素养培育的有效途径.

[关键词] 初中数学；发现学习；核心素养

初中数学教学中，对核心素养有两个层面的理解：一个层面是宏观层面，即根据核心素养的定义去强调其中的必备品格与关键能力；另一个层面是微观层面，也就是学科层面，即将数学学科核心素养的培育具体到数学抽象、逻辑推理与数学建模（通常对数学学科核心素养的界定是六个因素，但著名数学教育家史宁中先生认为这三个因素足以概括数学学科核心素养，笔者这里认同史教授的观点）等三个因素上来. 无论是宏观层面还是微观层面的理解，有一点是共同的，那就是核心素养是作为教学目标存在的，而如何实现这个目标则需要一线教师去摸索行之有效的途径. 结合已有的教学经验，梳理数学学科核心素养的三个关键要素作为关键能力（必备品格在关键能力形成的过程中自然体现）存在的意义，笔者以为发现教学可以成为实现核心素养培育的有效途径. 从这一思考出发，笔者进行了一定的实践与总结，发现有如下三点观念可以与同行分享.

发现学习与核心素养之间的良好契合

发现学习并不是一个新鲜事物，在中国教育引入布鲁纳教育理论的时候，发现学习就成为人们关注的热点. 需要注意的是，在历来的课程改革或教学改革中，发现学习都曾经以不同的形式成为教师或教育研究者关注的热点，这与发现学习自身的特性是分不开的.

所谓发现学习，布鲁纳定义为“通过运用自己的心智为自己获得知识的所有形式”. 通过这样的定义可以发现，发现学习并不是一个所谓的学习模式，其强调两个重点：一是运用自己的心智；二是为自己获得知识. 运用自己的心智意味着学生是学习的主体，而这与当前最先进的教育理念是一致的，这也是发现学习具有持久生命力的关键原因，而其目的是发现知识，在核心素养背景下，获得知识可以理解得更宽泛一些，即获得知识既包括建构学科知识，也包括形成学科思想方法与能力. 例如对于初中数学而言，学生在学习中固然要获得课程标准所规定的、教材所约定的所有的知识，同时也要在知识的学习过程中生成基本的数学能力，包括数学思想方法等.

举个例子，在“正方形”这一内容的学习中，掌握正方形的概念、性质和判定，并会利用它们进行基本的论证与计算，在理解正方形与平行四边形、矩形、菱形的联系与区别中生成比较能力与逻辑推理能力等，这是我们对课堂教学所界定的知识与能力目标. 为了达成这个目标，学生需要在自身自主学习的基础上，充分利用自己的心智（筆者以为这里所说的心智主要是指对自身经验与前概念的调用以及基本的逻辑推理能力等）来构建新知识. 通常情况下，正方形的定义是基于平行四边形而下的——有一组邻边相等，且有一个角是直角的平行四边形是正方形. 那学生在利用自己的心智获得这个定义的过程中，就需要对平行四边形及其性质有一个清晰的认识，同时要具有必要的推理能力与表象建构能力，即能够具有在自己的大脑中将一个平行四边形因为邻边相等且一个角为直角而变形为正方形的表象加工能力.

如果从核心素养的角度来看，这个正方形定义得出的过程中，因为学生思维加工的对象原本就是抽象的图形以及想象表象，因而具有高度的抽象性，具有数学抽象的基本特征；因为学生要根据定义去基于平行四边形而构建正方形（实际上也有部分学生是根据正方形的表象去理解如何由平行四边形得出正方形），所以这个过程中逻辑推理是客观存在的；而构建出来的正方形原本就具有数学模型的作用，因此这也可以视作是一个数学建模的过程. 于是就可以发现，在这样的一个发现学习的过程中，数学学科核心素养的三个基本要素都得到了体现，也因此我们可以认为，发现学习与数学学科核心素养的培育确实是比较契合的. 进一步就可以初步判断：利用发现学习来实现核心素养以及数学学科核心素养的培育是可行的.

利用发现学习培养核心素养教学尝试

一个猜想需要得到更多的实践才能被证实，在对发现学习的研究中，在核心素养培育的思考中，笔者建立的研究思路是：在日常教学中，并不刻意挑选某一个内容进行研究，而是随机地结合日常教学中的内容，然后思考是否有可能通过发现学习来培育数学学科核心素养（不一定是全部三个要素，也可以是其中一两个要素的培养）. 现以“平行四边形”这一内容的教学来说明.

平行四边形是人教版八年级下册的内容，由于学生此前已经具有了平行四边形的基础知识，在生活中也有一些平行四边形的体验，从而让他们大脑中具有一般的平行四边形的表象. 初中阶段平行四边形的学习，主要目标是能够灵活利用平行四边形的相关知识去解决数学习题与一些实际问题，其中平行四边形的性质与判定条件，以及两者之间存在的关系与区别，是教学的一个难点. 而重点的体现与难点的突破，也是利用发现学习来设计的一个重要原因.

在设计的时候，笔者特地进行了三步设计：

第一步是创设有效的情境，让学生在对平行四边形的思考过程中初步感知平行四边形的性质.

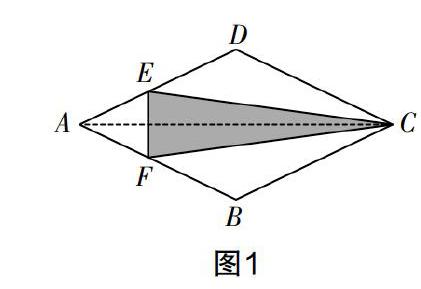
例如可以提供的情境是：小华在家里制作了一个四边等长的大风筝（这实际上是个菱形，因此这个素材在后面菱形知识的学习中还可以应用），如图所示，为了美观，他在风筝上面贴了一个彩色的三角形. 制作完成之后，小华将风筝拿给数学老师看，老师在表扬他的同时问他：“风筝中间的三角形的两边CE和CF相等吗？”小华一时无法判断，教师说只要有一把尺，不需要测出它们的长度也是可以判断的，你说小华应该怎么做呢？

这是一个来自于生活的情境，其可以让学生在对生活问题的思考中初步感知平行四边形的性质. 这里一个很重要的内在心理机制，就是利用学生的直觉去感知性质，这与数学学科核心素养中的直观想象是有联系的.

第二步，引导学生基于平行四边形的定义去推理平行四边形的性质.

初中阶段对“形”的研究，很多时候形的性质都来源于定义以及逻辑推理两个基础. 平行四边形被定义为两组对边分别平行的四边形，那学生自然可以得出“平行四边形对边互相平行”的性质，其后再借助于三角形全等的知识，亦不难发现“平行四边形的对边相等、对角相等”这一性质，在这个教学过程中，教师的一个重要思路，就是不要干预学生的思维，要让学生自己去主动探究，这样所得到的性质会让学生印象更加深刻. 而“平行四边形的对角线互相平分”这一性质较难发现，因此教师可以帮助引导一下——平行四边形的性质肯定是从边和角两个角度去描述的，除了平行四边形自身的四条边、四个角之外，我们还可以怎样描述它的性质呢？这种情况下学生容易想到利用对角线来得到更多的线与角，从而发现更多的性质. 而一旦对角线作出来，学生一样可以利用三角形全等去进行逻辑推理. 因此这个过程中，逻辑推理这一核心素养要素是体现得最为充分的.

第三步，基于原来的推理让学生反过来思考，从而引入平行四边形的判定.

平行四边形的性质得出，实际上是逻辑推理的结果，那如果将性质当作已知条件，那所得到的四边形是不是平行四边形呢？学生的思维自然也就指向了新的逻辑推理，为了让学生的思路变得更加清晰，教师可以明确引导学生从“边”和“角”两个角度去发现、組合条件，以寻找能够证明四边形为平行四边形的最简条件.

这是一个逆向推理的过程，也是一个平行四边形模型进一步明确的过程，待判定方法出来之后，还可以引导学生进一步思考刚开始创设的情境，看在刚开始的情境中，如果已知CE与CF相等，那还需要什么条件可以证实原四边形为平行四边形？

总之，通过这样的三步设计，学生在学习中既充分地调用了自己的心智，同时又获得了知识，更体现了数学抽象、逻辑推理与数学建模，因此较好地实现了基于发现学习培育数学学科核心素养的目的.

在核心素养培育过程中培养发现能力

发现学习是一种方式，核心素养是一种能力，其实发现本身就是一种能力，因而也可以认为发现本身就是核心素养的重要组成部分. 在这里，发现是与创造联系在一起的，因为创造本身也是一个心智高效参与并发现新知识的过程. 所以，核心素养培育的过程中，要高度重视学生发现能力的培养.

根据笔者的经验，初中数学教学中，利用数学探究，利用问题解决，是可以较好地让学生基于原有数学认知体系实现新的发现的，尤其是当学生沉浸在一个具体的问题情境中时，因为推理需要，他们有可能更充分地调用自己的数学知识去组合、试错，从而发现新的问题解决方法. 而当学生在证明过程中，在问题解决过程中发出“原来用的是这种方法”“原来还可以这样解”时，我们就认为他们是有发现的，发现能力是得到培养的.

总之，发现学习与核心素养在理论上的契合，能够得到实践的证明，也就是说发现学习是核心素养培育的重要途径.