从折纸活动中浅谈学生创造性思维的培养

冯世豪 卢德均

[摘 要] 勾股定理是初中数学一个重要的概念，笔者通过折纸活动中的数学经验，用折纸设计了一堂综合实践课，以探究勾股定理的多种证明方法，并在此过程中浅谈学生创造性思维的培养.

[关键词] 折纸；勾股定理；创造性思维

引言

《初中数学课程标准》（2011版）明确指出：“创新意识的培养是现代数学教育的基本任务，应体现在数学教与学的过程之中. 学生自己发现和提出问题是创新的基础；独立思考、学会思考是创新的核心；归纳概括得到猜想和规律，并加以验证，是创新的重要方法. 创新意识的培养应该从义务教育阶段做起，贯穿数学教育始终. ”现代折纸主要运用于科技、数学、教育、艺术四大领域，数学课上的折纸是学习意义上的折纸，能够为学生营造一个手脑并用的学习环境，能激发学生对数学的学习兴趣，能引发学生数学思考，能鼓励学生进行创造性思维，这也是笔者将折纸作为探索勾股定理教学素材的原因之一.

教学设计

1. 教学分析

刚升入初中的学生已掌握了一些简单几何图形的性质，为了增强学生的学习兴趣，提高学生对知识的应用能力，笔者将“用折纸来探索勾股定理”作为本堂课的内容.

2. 材料准备

为了方便学生观察，选取边长为15 cm且正、反两面颜色不同的双面正方形纸作为本节课的材料.

3. 学情分析

根据选材内容，将授课对象定为初中生. 在本堂课之前，学生掌握了一些简单几何图形的基本性质，以及求简单几个图形的面积公式.

4. 教学目标分析

《数学课程标准》（2011版）将综合实践课的教学目标分为知识技能、数学思考、问题解决、情感态度四个维度.

知识技能：在掌握正方形及等腰直角三角形性质的基础上理解折疊过程中的数学原理.

数学思考：通过问题驱动下的折叠与组拼过程，让学生学会独立思考，培养探索精神.

问题解决：从组拼出来的图案中发现勾股定理，运用两种求正方形面积的方法来解决简单的实际问题，增强应用意识.

情感态度：在问题驱动下的折叠与组拼过程中，提高动手操作能力，发散思维，体验成功的乐趣.

5. 教学重难点分析

教学重点：勾股定理内容的掌握.

教学难点：勾股定理的推导过程.

6. 教学方法

合作式探究.

7. 教学过程设计

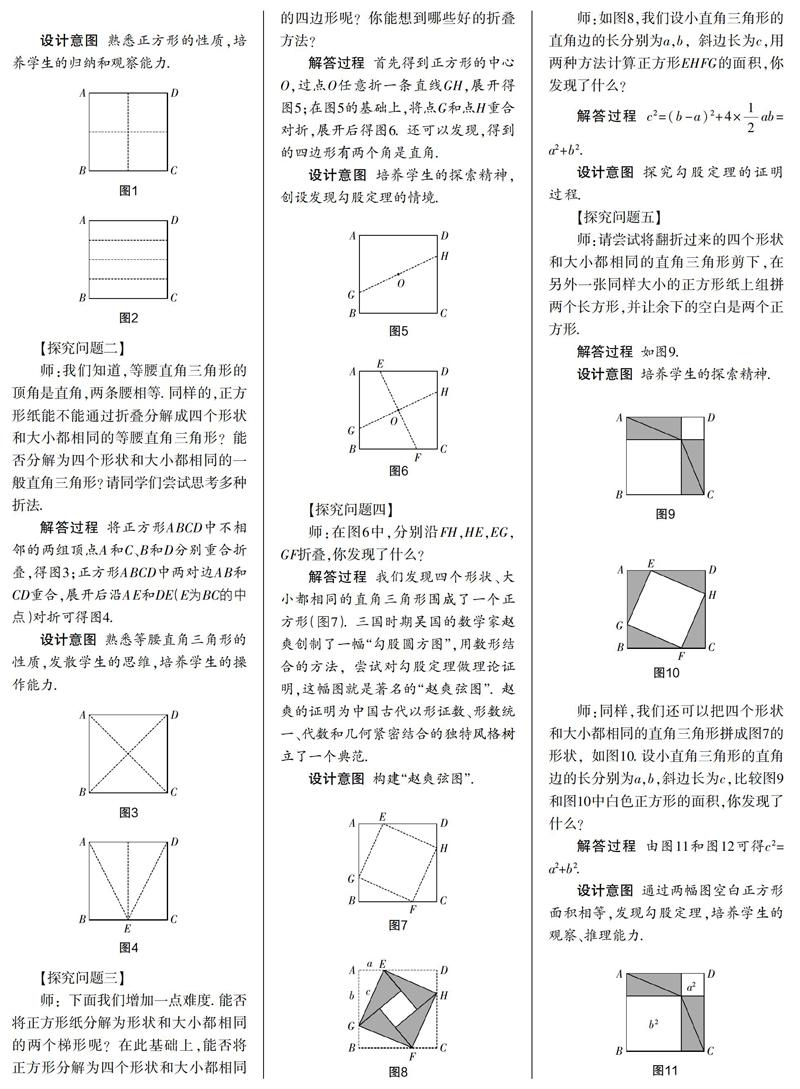
【探究问题一】

师：同学们，对于正方形，我们已经非常熟悉. 我们知道，正方形的四条边相等，四个角都为直角. 那么，一张正方形纸，能否通过折叠分解为四个形状和大小都相同的正方形？同样地，能否通过折叠，分解成四个形状和大小都相同的长方形？

解答过程 将正方形ABCD的对边AD，BC重合，可得一个长方形. 在此基础上，将长方形两条短边重合，展开后的折痕如图1；将长方形两条长边重合，展开后的折痕如图2.

设计意图 熟悉正方形的性质，培养学生的归纳和观察能力.

【探究问题二】

师：我们知道，等腰直角三角形的顶角是直角，两条腰相等. 同样的，正方形纸能不能通过折叠分解成四个形状和大小都相同的等腰直角三角形？能否分解为四个形状和大小都相同的一般直角三角形？请同学们尝试思考多种折法.

解答过程 将正方形ABCD中不相邻的两组顶点A和C、B和D分别重合折叠，得图3；正方形ABCD中两对边AB和CD重合，展开后沿AE和DE（E为BC的中点）对折可得图4.

设计意图 熟悉等腰直角三角形的性质，发散学生的思维，培养学生的操作能力.

【探究问题三】

师：下面我们增加一点难度. 能否将正方形纸分解为形状和大小都相同的两个梯形呢？在此基础上，能否将正方形分解为四个形状和大小都相同的四边形呢？你能想到哪些好的折叠方法？

解答过程 首先得到正方形的中心O，过点O任意折一条直线GH，展开得图5；在图5的基础上，将点G和点H重合对折，展开后得图6. 还可以发现，得到的四边形有两个角是直角.

设计意图 培养学生的探索精神，创设发现勾股定理的情境.

【探究问题四】

师：在图6中，分别沿FH，HE，EG，GF折叠，你发现了什么？

解答过程 我们发现四个形状、大小都相同的直角三角形围成了一个正方形（图7）. 三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”，用数形结合的方法，尝试对勾股定理做理论证明，这幅图就是著名的“赵爽弦图”. 赵爽的证明为中国古代以形证数、形数统一、代数和几何紧密结合的独特风格树立了一个典范.

设计意图 构建“赵爽弦图”.

师：如图8，我们设小直角三角形的直角边的长分别为a，b，斜边长为c，用两种方法计算正方形EHFG的面积，你发现了什么？

解答过程 c2=（b-a）2+4×ab=a2+b2.

设计意图 探究勾股定理的证明过程.

【探究问题五】

师：请尝试将翻折过来的四个形状和大小都相同的直角三角形剪下，在另外一张同样大小的正方形纸上组拼两个长方形，并让余下的空白是两个正方形.

解答过程？摇 如图9.

设计意图 培养学生的探索精神.

师：同样，我们还可以把四个形状和大小都相同的直角三角形拼成图7的形状，如图10. 设小直角三角形的直角边的长分别为a，b，斜边长为c，比较图9和图10中白色正方形的面积，你发现了什么？

解答过程 由图11和图12可得c2=a2+b2.

设计意图 通过两幅图空白正方形面积相等，发现勾股定理，培养学生的观察、推理能力.

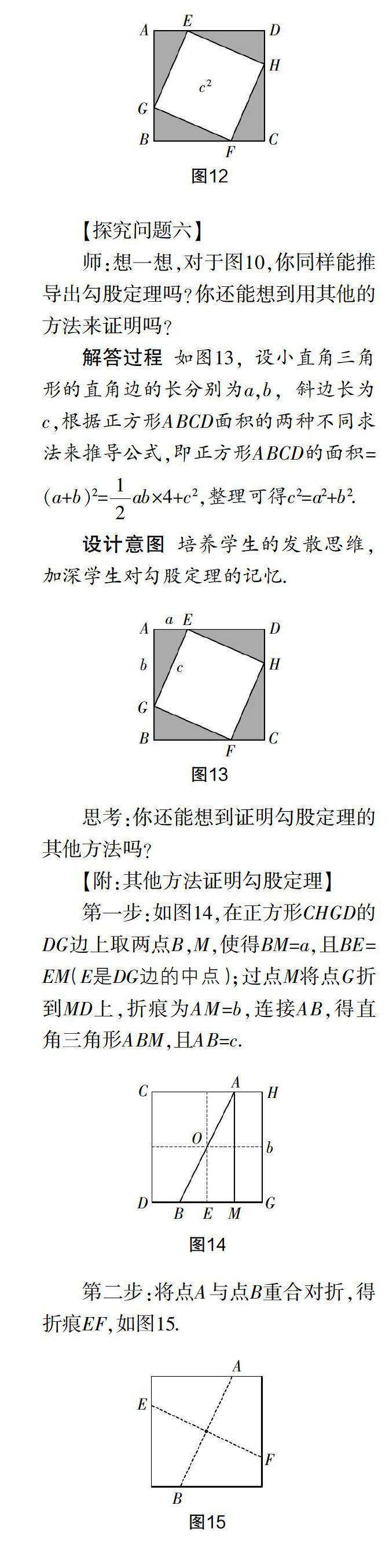
【探究问题六】

师：想一想，对于图10，你同样能推导出勾股定理吗？你还能想到用其他的方法来证明吗？

解答过程 如图13，设小直角三角形的直角边的长分别为a，b，斜边长为c，根据正方形ABCD面积的两种不同求法来推导公式，即正方形ABCD的面积=（a+b）2=ab×4+c2，整理可得c2=a2+b2.

设计意图 培养学生的发散思维，加深学生对勾股定理的记忆.

思考：你还能想到证明勾股定理的其他方法吗？

【附：其他方法证明勾股定理】

第一步：如图14，在正方形CHGD的DG边上取两点B，M，使得BM=a，且BE=EM（E是DG边的中点）；过点M将点G折到MD上，折痕为AM=b，连接AB，得直角三角形ABM，且AB=c.

第二步：将点A与点B重合对折，得折痕EF，如图15.

第三步：沿折痕EF和AB剪成四个全等的四边形，按图16拼图便可得到勾股定理.

如何培养学生的创造性思维

美国著名心理学家、美国心理学会会长吉尔福特对于创造性思维的研究具有深远的影响. 他在“智力的三维结构”模型中提出了创造性思维. 他认为，创造性思维是指从给定的信息中产生新信息，其着重点是从同一来源中产生各种各样的为数众多的输出. 创造性思維具有流畅性、灵活性、独创性三个最主要的特征.

折纸作为一种教学工具用于数学教学活动中，引导学生观察折痕所形成的边角关系，帮助学生构建折纸拼图活动与数学内容的联系，培养学生的动手能力、观察能力、想象能力和创造性思维能力. 下面，笔者从本节课出发，浅析如何真正培养学生的创造性思维.

1. 流畅性

流畅性是指在规定时间内产生有效图形信息的个数. 我们说创造性思维流畅，指的是遇到问题时，心智活动少阻塞，多流畅，在短时间内能够找到知识之间的多个联系，能产生较多的可供选择的解决方案. 本节课营造的是一种探究式课堂，课堂开始对一张正方形纸进行四等分，从正方形、长方形到等腰三角形、直角三角形，一直到梯形、一般四边形，不仅为后面折叠“赵爽弦图”埋下伏笔，更在于启发学生思考一张正方形纸可以四等分为哪些图形，能训练学生的创造性思维.

2. 灵活性

灵活性是指在规定时间内产生有效图形信息的种类. 我们说图形创造性思维变通，是指遇到困难时能够随机应变，及时调整解题思路或解题方法，能从多个方向、多个方面思考问题，能产生多种不同类型的可供选择的解决方案，能用不同类型的方法解决问题，或能得到不同类型的答案. 灵活性和流畅性的主要区别在于，提供选择的方案、方法、答案的性质有所不同.

本节课可归纳为解决两个大问题，一是将正方形纸四等分成多种图形的折叠方法，二是探究勾股定理的多种证明方法. 笔者通过与某中学初中数学教师交流，在某班进行了一堂课的教学. 在与学生交流中发现，在第一个问题中，学生的折叠方法多样，通过教师的引导，能够思考正方形纸与目标图形之间的关联，并按照正方形点、边、角之间的关系，平面几何图形的性质等数学知识去尝试折叠；对于第二个问题，勾股定理的证法多样，需小组合作探究、上台展示、教师归纳总结. 这两个问题的解答过程，都锻炼了学生创造性思维的灵活性，总体上来说，整堂课达到了预期设想的效果.

3. 独创性

独创性是指在规定时间内产生新颖、独特、有效信息的个数. 我们说图形创造性思维独特，是指在解决图形问题时，能突破常规和经验的束缚，用新的观点、新的方法、新的思路解决问题，或得出新颖、独特、稀有的答案，创造性成分中最重要的是独创性. 对于创造性思维水平的测量，到目前为止，独创性的测量一直是学术界的难点. 对于教师来说，在教学过程中多提出能真正启发学生创造性思维的问题，多鼓励学生积极思考，多留时间给学生思考，才能更好地进行师生互动，从而上好“探究型”课.

结语

林崇德先生说：“素质教育是以创新精神为主题的教育，学生不仅仅应该拥有学习的能力，更应该有实践和创新的能力. 开展具有创造性的数学活动，能够激发学生在数学学习中的创造力.”就本堂课而言，把几何图形的性质以及求面积公式等数学知识运用到折纸活动当中，不仅能将数学知识、思维方法迁移到应用实际问题当中，而且能让学生形成学习新知识的能力，从中培养学生的创造性思维.