冰川分布格局对地理因子响应机制

张正勇，刘琳，徐丽萍

石河子大学，新疆 石河子 832000

冰川分布格局是水循环系统的重要组成部分，也是气候变化背景下冰冻圈科学研究的热点问题之一（施雅风等，2006；秦大河等，2009；Katel，2015）。冰雪作为一种特殊下垫面，通过反射太阳辐射和消融耗热的方式影响局地气候乃至全球气候变化，而其本身也是区域气候变化的产物之一（王圣杰等，2011；杨东，2013）。区域地理位置和地形因子对冰川发育和演化具有极为重要的作用。冰川消融-积累变化过程可导致河川径流在季节上的重新分配（谢昌卫，2004），异常的雪盖或者融雪期的前后移动如果与强降水事件重合，有可能引发洪水，对陆面水文过程产生十分重要的作用（Clague et al.，2000；Owen et al.，2009）。

目前，遥感技术（RS）是获取冰川变化信息的主要技术手段，卫星数据在雪盖制图、动态监测、融雪径流模拟和灾害监测评估等方面研究中已被广泛应用（Paul et al.，2009；怀保娟等，2014）。众多学者基于地理信息系统技术（GIS）和数字高程模型（DEM）数据研究不同地形对冰川变化的影响（Schneider et al.，2008；王璞玉等，2014，尹振良，2016），运用数理统计方法（模型）分析了区域冰川变化对气候的响应机理（Yao et al.，2004），并取得了丰富的成果。然而，冰川分布格局是区域地理位置、地形和气候等多因子共同作用的结果。以往就冰川变化及其影响因子的相关研究多采用常规统计回归方法，该方法在因子明确且相互独立时建模效果较好，但由于波段参数或各气候及地形因子之间往往存在多重相关性，必然造成模型稳定度差、精度不高和模型难以解释等不足。而被誉为第二代统计回归分析方法的偏最小二乘法（以下简称PLS）能克服因子多重相关性，该方法是一种集主成分分析、多元线性回归分析和典型相关分析的基本功能于一体的新型多元统计分析方法。它允许在样本点个数少于变量个数的条件下进行回归建模且最终模型中包含原有的所有自变量（任若恩等，1997；王惠文，1999）；同时，它能对系统中的数据信息进行分解和筛选，提取对因变量解释性最强的综合变量，辨识系统中的信息和噪声。另外，它还能通过数据分析简化数据结构，反映因变量和自变量之间的函数关系，使模型的稳健性、精度、实用性得到提高（张旸等，2004；舒守娟等，2007）。PLS已被广泛应用于经济、化学、水利、地理等领域的研究中（王惠文，1999；蒋国兴，2007；梁秀娟，2008）。

本研究以新疆玛纳斯河流域（以下简称玛河流域）为样本区，借助RS和GIS技术提取冰川信息并分析冰川分布格局特征，并基于PLS构建冰川分布模型，探究干旱区冰川分布格局及其对区域地理位置、地形和气候因子的响应机理，以期为区域气候和水文研究提供参考。本研究对干旱区水资源的合理利用具有重要意义。

1 研究区及研究方法

1.1 研究区概况

玛纳斯河流域位于天山北麓中段，地处准噶尔盆地南缘，地理位置为 84°43′～86°35′E，43°21′～45°20′N（图1），远离海洋，干旱少雨，蒸发量大，多荒漠，属典型的大陆性干旱气候区。经过新生代以来的构造运动、气候变化等作用，流域内形成了具有明显分带性的地貌格局。径流补给具有显著的垂直地带性，冰雪融水对河流的补给占径流量的35.3%，流域内自东向西分布有塔西河、玛纳斯河、宁家河等6条内陆河流。据中国冰川目录统计数据显示，玛纳斯河是准噶尔内流水系中冰川数量最多和规模最大的河流。

1.2 研究方法

本研究根据冰川遥感反演原理，采用较高分辨率的 TM影像、DEM数据和气象数据，分析冰川与敏感波段及波段组合参数、地形参数及气候参数的统计关系，借助RS和GIS技术提取冰川信息并抽取样点，基于PLS构建冰川-地形-气候统计分布模型，并进行模型有效性和适用性检验，试图揭示干旱区冰川分布格局对其影响因子的响应机理。

2 数据说明及处理

2.1 数据说明

影像数据为2006年7月15日和2010年7月20日的Landsat-5影像，数据来自中国科学院对地观测与数字地球科学中心存档卫星遥感数据目录服务系统（http://ids.ceode.ac.cn/）。DEM包括SRTM3 V4.1数据，分辨率为90 m，来自中国科学院计算机网络信息中心国际科学数据镜像网站（http://datamirror.csdb.cn）。气象数据包括玛河流域及周边13个气象站点（图1）的月降水量、月均温等数据，来源于国家气象信息中心（http://www.nmic.gov.cn/）。

2.2 数据处理

2.2.1 气温和降水数据计算

冰川的消融-积累变化过程受到气温和降水的著显影响。由于高海拔山区气象数据缺失，本研究采用传统气温线性模型（杨昕等，2007）和降水回归模型（舒守娟等，2005）估算研究区气温和降水数据并进行栅格计算，通过对估算的气候数据和气象站点实测数据的误差分析发现，气温和降水的平均误差分别为0.23 ℃和1.52 mm，平均相对误差分别为1.14%和1.02%，分别对两个模型进行了F检验，均通过置信度为0.95的相关性检验，估算数据满足精度需求。

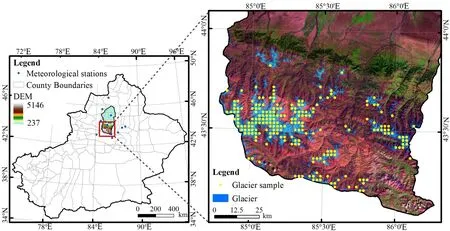
图1 研究区示意图Fig.1 The sketch map on the study area

2.2.2 地理位置及地形参数计算

冰川分布具有一定的地形特征，高程是主要的地形因子，同时，坡向和坡度也有一定影响。利用ArcGIS的Conversion Tools工具，由SRTM提取DEM网格中心点的经度、纬度数据。借助ArcGIS 3D分析工具，由DEM提取玛河流域山区坡度和坡向。坡向β有如下规定：以正南为0°，沿顺时针方向为正，具体规定为-22.5°≤β≤22.5°为南向坡，22.5°≤β≤67.5°为西南向坡，其余类推。

2.2.3 冰川分布格局信息提取及样点分布

借助ENVI 4.8软件对TM影像进行辐射校正，然后对影像进行波段组合和线性拉伸，采用面向对象法对影像进行冰川分布格局信息提取。本研究考虑到遥感影像解译过程中积雪对冰川边界的干扰，选取的遥感影像均为夏季时段（7月底）数据，且归一化冰雪指数（NDSI）在提取冰川信息中已有良好的精度和广泛的应用，故本文以NDSI表征冰川信息，并根据下式在ArcGIS中计算冰川区的NDSI。

结果显示，本研究分类总体精度达到87.59%，Kappa系数为0.8396，满足分类精度。

采用 ArcGIS软件绘制研究区渔网并提取其中心点，与所提取的研究区冰川分布格局信息叠加相交后获取了布局均匀的冰川样点213个（图1），最后获取各样点的地理位置（经纬度）、地形特征（高程、坡度和坡向）、NDSI、气温和降水等属性信息。

3 统计分析与PLS建模

玛河流域上游山区的天山支脉喀拉乌成山、依连哈比尔尕山及比依克山等海拔为5000～5500 m，为天山山区第二大高山带山结，其冰川总面积仅次于托木尔峰地区。特殊的地形特征决定了研究区冰川分布与高程、坡度、坡向等具有复杂的相关关系，且山体南北跨度较大，也应考虑地理位置（经度和纬度）对冰川分布格局的影响，同时气温和降水也对冰川分布具有显著作用。为了揭示研究区冰川分布格局特征及成因，采用PLS统计方法，建立区域地理位置、地形、气候因子与冰川分布模型，其中冰川分布（NDSI）为因变量，自变量包括三类，即地理位置因子包括纬度（φ）和经度（λ），地形因子包括高程（h）、坡度（α）和坡向（β），气象因子包括年均温（t）和年降水（p）。地理位置因子反映气候和环流的大背景，地形因子反映局地地形的影响，气候因子反映冰川形成的气候条件。

3.1 统计分析

在运用传统多元统计回归法进行模拟估算的过程中，由于自变量系统的解释性不够和自变量之间的多重相关性考虑不全面，使得估算值与实测值之间存在较大误差（张旸等，2004）。由于冰川覆盖区地形复杂程度较高，间接造就了局地地形和局地气候诸因子间的复杂关系，故建模之前进行自变量多重相关性分析。

多元线性相关系数是用于衡量多个变量间线性相关强弱的无量纲指标，能够较全面地反映变量间的线性相关强度。表1所示为玛河流域7个因子（自变量）与7月NDSI（因变量）的相关系数矩阵，其中，r(λ,p)=-0.494，r(β,t)=-0.995，r(β,p)=0.621，r(t,p)=-0.625，可见自变量之间存在着多重相关性。此外，基于最小二乘法（OLS）建立的线性回归的总模型R2较大，F统计量高度显著，且F检验表明模型与数据的拟合程度较好，线性关系显著，可用线性模型进行描述。然而，表2显示，纬度（φ）、坡向（β）和平均气温（t）容差均小于 0.10，方差膨胀因子（Variance Inflation Factors，简记作VIF）基本均大于10，且后3个因子特征值很小，条件指数均大于 100，说明因子之间存在严重的多重共线问题。另外，因子φ（纬度）和β（坡向）的t检验值均小于临界值1.653，均未通过t检验，说明这两个因子对NDSI的线性影响不显著；而其他因子的回归系数为零的概率（Sig.）均大于 0.05，说明数据之间差异性不显著，对NDSI的预测力度不理想，在回归方程中不具有统计学意义。以上结果显示了因子多重相关性的典型病兆，若基于OLS建模则需考虑剔除纬度和坡向因子。然而，纬度和坡向变化对冰川区获得直接太阳辐射具有明显影响，如果剔除φ和β则不能准确反映冰川分布变化情况。可见，自变量的多重相关性使得一些对因变量有重要解释意义的因子未能被基于OLS的回归模型所考虑，这便会影响模型的精确性和实用性。为有效克服自变量多重相关性的问题，本研究采用PLS法构建回归模型。

表1 研究区样点地理、地形及气候因子与NDSI的多重相关系数矩阵Table1 Multiple correlation coefficient matrix about geographical position, terrain, climate factors and NDSI of sampling points in the study area

表2 最小二乘法（OLS）回归建模的系数、t检验、VIF及条件指数Table2 The regression modeling index coefficient, t test, VIF, and conditional by method of least squares (OLS)

3.2 PLS建模及检验

3.2.1 PLS建模

PLS法建模集成了多元线性回归分析、典型相关分析和主成分分析等方法的优点。基于典型相关分析和主成分分析，首先寻找自变量X中存在的多重共线性关系，然后从X中提取成分t1，它既是自变量的线性组合也能最大程度地携带X中的数据变异。假定估计量Y=1tB，再在t1对Y有最大解释能力即达到最大相关度下实施Y对t1的回归，得到Y=BPLS1t1+eY，最后进行交叉有效性检验，如果方程未达到满意的精度，则利用X和Y被t1解释后的残余信息eX和eY进行第二轮成分提取，直到达到满意精度。最终，若通过交叉有效性检验的成分个数为m，则估计量：

再还原成关于原始变量的回归方程Y=BPLSX+ePLS，这样便完成了PLS回归建模。

建模之前要对偏最小二乘回归因子进行精度分析，以选取信息和解释能力较强的因子作为典型成分。本文利用SIMCA-P 12数据分析软件进行偏最小二乘因子回归分析。其精度分析运行结果表明（表3），第一主成分tl解释了原自变量系统中43.4%的变异信息，同时，解释了因变量系统中75%的变异信息；第二主成分t2解释了原自变量系统中27%的变异信息和因变量系统中3.2%的变异信息；第三主成分t3解释了原自变量系统中 9.9%的变异信息和因变量系统中 0.3%的变异信息；第四主成分t4解释了原自变量系统中 0.4%的变异信息和因变量系统中2.9%的变异信息；前4个偏最小二乘因子可解释X变异的程度达80.7%，对Y的解释变异累计百分比达81.4%，已经涵盖了主要的自变量组和因变量组的数据信息，而继续添加t5、t6和t7，对X和Y变差的贡献值都很小。由此可见，前4个被抽取的成分综合了自变量组和因变量组的大部分信息，对结果分析有重要的作用。

在实现数据结构的简化和两组变量间的相关分析后，可以通过对回归方程的优化，找到因变量与自变量之间的函数关系，建立回归模型用于预测（王惠文，1999）。通过计算得出的PLS回归因子解释的变差百分比及Q2统计结果（表3），可以评价建模所取自变量成分对因变量的解释能力以及交叉有效性判断模型的总预测能力。模型对 NDSI的预测能力是否能通过交叉有效性检验，主要取决于Q2值的大小，Q2越大说明模型对NDSI的预测能力越强，其可信度和可行性也就越强。由表3统计结果可知，前两个成分即能够解释78.2%以上因变量的变异，Q2最高达到 0.769，说明此模型对NDSI的解释性较强，能够通过交叉有效性检验。而其后的成分对总的预测能力不仅没有正面贡献，还使总预测能力下降，因此仅选用前两个成分进行建模。

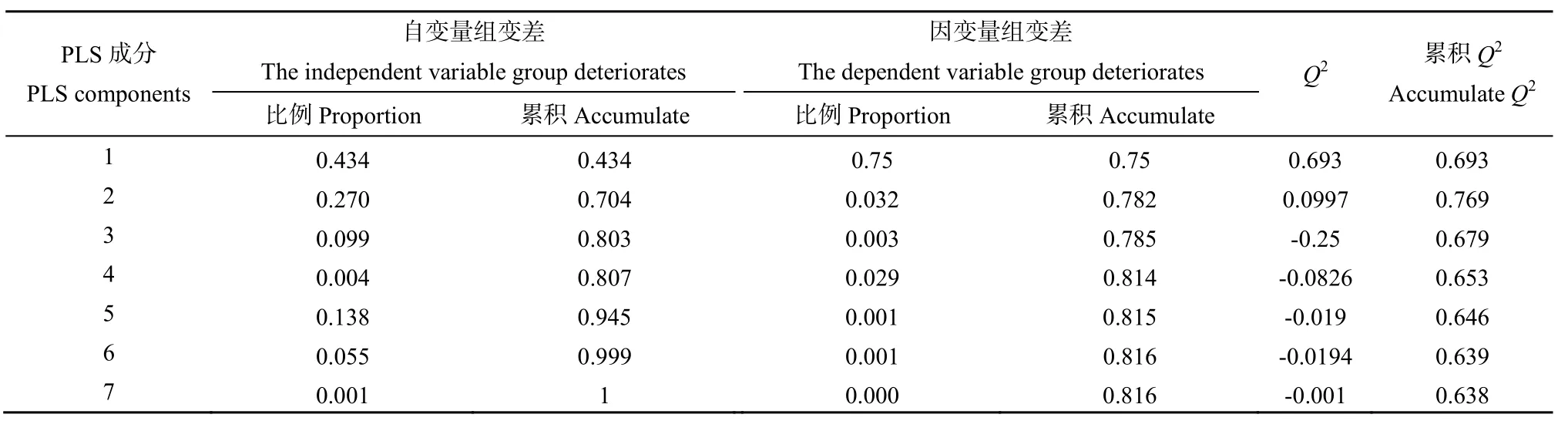
表3 偏最小二乘回归因子解释的变差百分比及Q2统计Table3 Percent variation accounted for factors by partial least squares and its Q2 statistics

利用SIMCA-P 12进行具有交叉验证的PLS模型拟合，得到研究区2006年7月NDSI的空间分布估算模型，即NDSI-地形-气候模型（式2）。式中各系数不但可以反映研究区NDSI空间分布，且其正负值还表征各因子对因变量的贡献程度及其相关性。

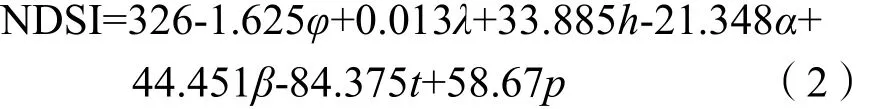
3.2.2 模型适用性检验

虽然该模型能够解释 78.2%以上的因变量变异，对样区冰川格局的总预测能力达到76.9%，但是模型的精度和稳定性还有待进一步验证。为了检验模型的适用性，将 2010年年均气温和降水量等数据资料输入PLS模型进行模拟预测，并采用之前处理TM影像的方法对2010年影像进行解译分类，最后计算NDSI并与影像提取的实际冰川分布信息进行对比（图2）。由图2和表4可知，模型计算的冰川面积和斑块数目均小于影像提取结果，平均斑块面积却大于影像提取结果，说明模型未能计算出所有冰川区域，实际冰川更为破碎。高山区典型冰川提取效果较好，而低山、中山区的面积较小，零散孤立的冰川未被计算在内。其原因在于样点主要分布在大片典型冰川中，低山区小面积冰川样点分布较少，且山区地形复杂导致了误差的产生。总体而言，该模型在对干旱区冰川分布格局及其影响因子的相关性方面具有较好的分析能力，对冰川变化及其机理分析有较高的可信度。

4 讨论

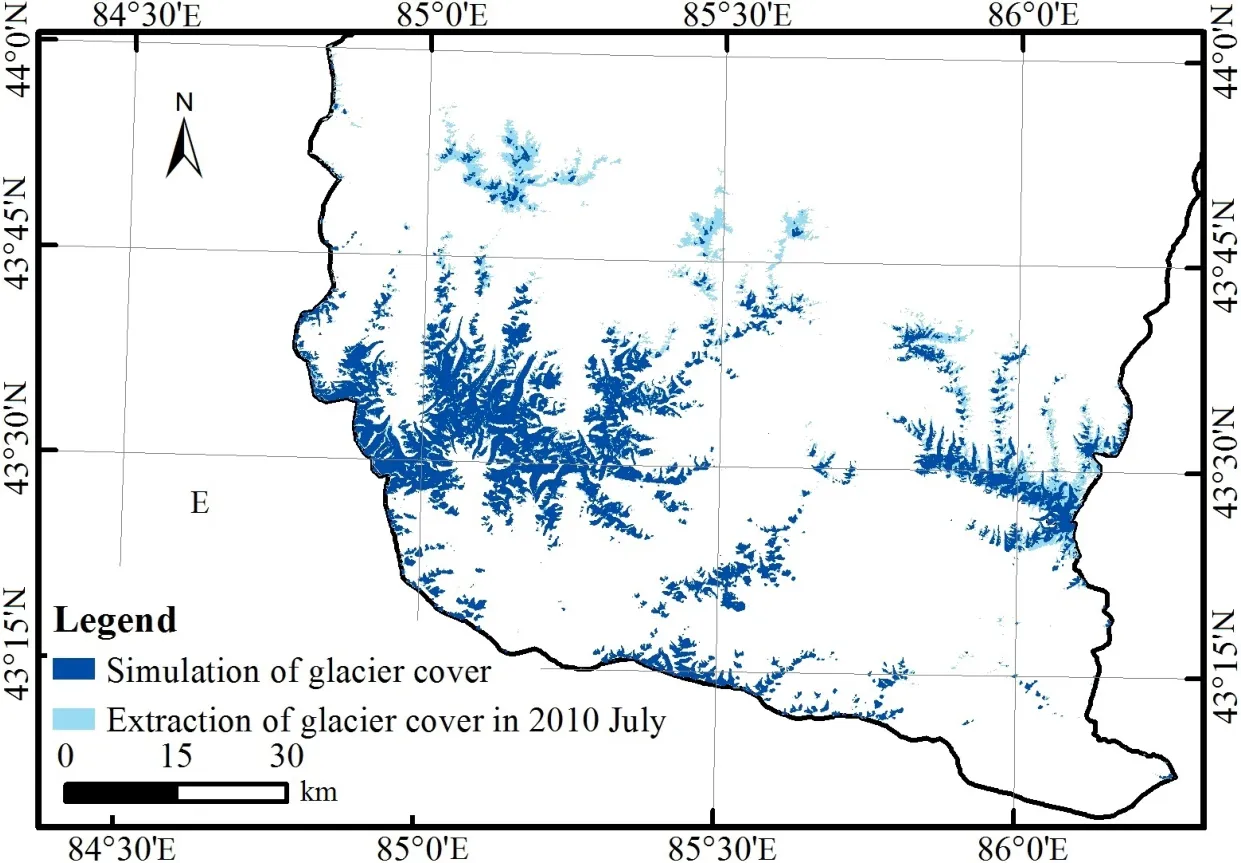
图2 模型估算结果与影像提取结果空间对比Fig.2 Space comparison between model estimation results and image extraction results

表4 模型估算结果与影像提取结果比较Table4 Model estimation results and image extraction results

冰川面积变化是多因子共同作用造成的，大量研究认为，气候变化是其主要影响因子，气温对时间尺度和空间跨度较大的冰川的进退作用明显，而降水对短期和范围较小的冰川的进退作用明显（高晓清等，2000；王圣杰等，2011）。中国天山和祁连山山区冰川变化研究显示，小规模冰川变化对气候响应更敏感，面积小于1 km2的冰川萎缩是山区冰川面积缩小的主要原因，朝北（阳坡）冰川面积缩小最多（孙美平等，2015；邢武成等，2017）。本文通过PLS构建模型发现，温度（t）和坡度（α）与NDSI呈负相关，海拔（h）、降水（p）等因子与冰川面积分布呈正相关；随纬度（φ）的递增，冰川面积呈缩小态势，这是由于山体南坡为阳坡，冰川消融速率较高；就经度（λ）变化而言，研究区东部冰川分布面积大于西部。气候变化是影响研究区冰川格局的最重要因素，其中，年均温的贡献最大，降水增加虽然会扩大冰川面积，但还是无法抵消温度升高对研究区冰川消融的影响。随海拔升高，气温降低，冰川累积量和存量增多；坡度对冰川的形成和发育有很大影响，缓坡有利于冰川的累积和稳定，进而可形成面积更大的单条冰川；坡体朝向决定着山区太阳辐射的获得量，使得山区阴坡和阳坡冰川消融速率存在较大差异；而经度和纬度对模型的解释量最小，与模型的相关程度也最低，可能是由于研究区域面积较小，地理因子的变化对冰川不够敏感，倘若研究区域面积更大则地理位置因子对冰川分布格局的解释能力会增强。综上，地理位置要素对冰川的贡献相对较小，地形因子对冰川的发育和积累具有决定性作用，而气候因子是影响冰川分布格局动态变化的最重要因子，对模型的解释有至关重要的作用。

本研究在建模过程中对影响冰川的大多数相关因子进行了分析研究，发现这些相关因子作为自变量对冰川分布格局动态变化的解释量为 78.2%，模型的总预测能力为 76.9%，即存在其他影响冰川格局变化的因子未被纳入此模型，如风向、风力、水汽压、相对湿度及下垫面性质等，需要在以后的研究中不断完善模型，使其能更好地预测和模拟冰川分布格局。此外，本文研究所选用的站点数据是玛纳斯河流域及周边13个气象站点的数据，由于气象站点较少，样本数不足且分布不均匀，加之研究区内几乎没有高海拔站点，对高海拔地区气候数值的模拟存在不确定性，故影响了模型的预测能力。

5 结论

玛河流域地形复杂，气候变化较为活跃，综合自然地理环境对研究区冰川分布格局的影响极为复杂。本研究运用 PLS回归分析法构建的冰川-地形-气候模型具有较高的有效性和适用性，模型总体预测能力达到76.9%，模拟结果显示：气候变化是影响研究区冰川分布格局动态变化的最重要因子，地形因子对冰川的发育和积累具有决定性作用，而地理位置要素对冰川的贡献相对较小。

尽管在建模过程中没有包含更多自变量以及部分数据精确度有待商榷，使得该模型的精确性和稳健性还存在一定不足，但研究结果对探究干旱区冰川变化对地形和气候的响应机理具有参考价值。同时，对于遥感数据缺失的区域或时段，只要有DEM、温度和降水数据，即可借助该模型反演冰川分布格局，因此本模型具有一定的应用价值和推广意义。

参考文献：

BERTHIER E, AMAUD Y, BARATOUX D, et al. 2004. Recent rapid thinning of the “Mer de Glace” glacier derived from satellite optical images [J]. Geophysical Research Letters, 31(2): 174-182.

CLAGUE J J, EVANS S G. 2000. A review of catastrophic drainage of moraine-dammed lakes in British Columbia [J]. Quaternary Science Reviews, 19(4): 1763-1783.

KATEL N I I. 2012.Possibility of operative treatment of geriatric patients with critical lower limb ischemia[J]. 25(2): 338-42.

Li Z S, WANG Z Q. 1998.Measurements of Glacier Variation in the Tibetan Plateau Using Lands at Data [J]. Remote Sensing of Environment,63(1): 258-264.

OERLEMANS J. 1994.Quantifying global wanning from the retreat of glaciers[ J]. Science, 264(4): 243-245.

OERLEMANS J. 2005. Extracting a Climate Signal from 169 Glacier Records [J]. Science, 308(2): 675-677.

OWEN L A, THACKRAY G, ANDERSON R S, et al. 2009. Integrated research on mountain glaciers: Current status priorities and future prospects [J]. Geomorphology , 103(3): 158-171.

PAUL F, ANDERSON L M. 2009. A new glacier inventory for the Svartisen region, Norway, from Landsat ETM+ data; challenges and change assessment [J]. Journal of Glaciology, 55(5): 607-618.

RICHARDSON S D, REYNOLDS J M. 2000.An overview of glacial hazards in the Himalayas [J]. Quaternary International, 65(4): 31-47.

SCHNEIDER D, GRANADOS D H, KSAB A. 2008. Assessing lahars from ice-capped volcanoes using ASTER satellite data, the SRTM DTM and two different flow models: case study on Iztaccihuatl (Central Mexico)[J]. Natural Hazards and Earth System Sciences, 8(1): 559-571.

THOMPSON L G, YAO T D, MOSLEY-THOMPSON E, et al. 2000. A High-Resolution Millennial Record of the South Asian Monsoon from Himalayan Ice Cores [J]. Science, 289(3): 1916-1919.

YAO T D, WANG Y, LIU S P, et al. 2004. Recent glacial retreat in High Asia in China and its impact on water resource in Northwest China [J].Science in China Series D: Earth Sciences, 47(5): 1065-1075.

YE Q K, CHEN S, WANG F J.2006. Monitoring glacier variations on Geladandongmountain, central Tibetan Plateau, from 1969 to 2002 using remote-sensing and GIS technologies [J]. Journal of Glaciology,52(3): 537-545.

包为民, 瞿思敏. 2001. 冰川消融耦合模型研究[J]. 水科学进展, 12(3):318-323.

高晓清, 汤懋苍, 冯松. 2000. 冰川变化与气候变化关系的若干探讨[J].高原气象, 5(1): 9-16.

怀保娟, 李忠勤, 孙美平, 等. 2014. 近 50年黑河流域的冰川变化遥感分析[J]. 地理学报, 69(3): 365-377.

蒋国兴. 2007. 偏最小二乘回归方法 (PLS) 在短期气候预测中的应用研究[D]. 南京: 南京信息工程大学: 41-48.

李占清, 翁笃鸣. 1987. 一个计算山地地形参数的计算机模式[J]. 地理学报, 42(3): 269-278.

梁秀娟. 2008. 基于偏最小二乘回归分析的城市经济分析[D]. 武汉: 华中科技大学: 23-27.

刘时银, 鲁安新, 丁永建, 等. 2002. 黄河上游阿尼玛卿山区冰川波动与气候变化[J]. 冰川冻土, 24(6): 701-707.

蒲健辰, 姚檀栋, 段克勤, 等. 2005. 祁连山七一冰川物质平衡的最新观测结果[J]. 冰川冻土, 27(2): 199-204.

秦大河, 丁永建. 2009. 冰冻圈变化及其影响研究——现状、趋势及关键问题[J]. 气候变化研究进展, 5(4): 187-195.

任若恩, 王惠文. 1997. 多元统计数据分析——理论方法实例[M]. 北京:国防工业出版社: 46-57.

施雅风, 崔之久, 苏珍. 2006. 中国第四纪冰川与环境变化[M]. 河北科学技术出版社: 48-51.

施雅风. 2000. 中国冰川与环境-现在、过去和未来[M]. 北京: 科学出版社: 12-15.

舒守娟, 王元, 熊安元. 2007. 中国区域地理、地形因子对降水分布影响的估算和分析[J]. 地球物理学报, 50(6): 1703-1712.

舒守娟, 喻自凤, 王元, 等. 2005. 西藏地区复杂地形下的降水空间分布估算模型[J]. 地球物理学报, 48(3): 535-542.

孙美平, 刘时银, 姚晓军, 等. 2015. 近 50年来祁连山冰川变化—基于中国第一、二次冰川编目数据[J]. 地理学报, 70(9): 1402-1414.

王惠文. 1999. 偏最小二乘回归方法及其应用[M]. 北京: 国防工业出版社: 58-66.

王璞玉, 李忠勤, 高闻宇, 等. 2011. 气候变化背景下近50年来黑河流域冰川资源变化特征分析[J]. 资源科学, 33(3): 399-407.

王璞玉, 李忠勤, 周平, 等. 2014. 近期新疆哈密代表性冰川变化及对水资源影响[J]. 水科学进展, 25(4): 518-525.

王圣杰, 张明军, 李忠勤, 等. 2011. 近50年来中国天山冰川面积变化对气候的响应[J]. 地理学报, 66(1): 38-46.

王宗太, 刘潮海, 尤根祥, 等. 1981. 中国冰川目录连山区[M]. 兰州: 中国科学院兰州冰川冻土研究所: 56-67.

夏丽莎. 2008. 基于偏最小二乘的武汉城市圈经济研究[D]. 武汉: 华中科技大学: 33-37.

谢昌卫, 丁永建, 刘时银, 等 2004. 韩海东.托木尔峰南坡冰川水文特征及其对径流的影响分析[J]. 干旱区地理, (04): 570-575.

谢自楚, 刘潮海. 2010. 冰川学导论[M]. 上海: 上海科学普及出版社:7-15.

邢武成, 李忠勤, 张慧, 等. 2017. 1959年来中国天山冰川资源时空变化[J]. 地理学报, 72(9): 1594-1605.

杨东, 王慧, 程军奇, 等. 2013. 近 50年青海省气候变化特征及其与ENSO的关系[J]. 生态环境学报, 22(04): 547-553.

杨昕, 汤国安, 王春, 等. 2007. 基于 DEM 的山区气温地形修正模型——以陕西省耀县为例[J]. 地理科学, 27(4): 525-530.

姚檀栋, 段克勤, 田立德, 等. 2000. 达索普冰芯积累量记录和过去400a来印度夏季风降水变化[J]. 中国科学(D辑: 地球科学), 30(6):619-627.

尹振良, 冯起, 刘时银, 等. 2016. 水文模型在估算冰川径流研究中的应用现状[J].冰川冻土, 38(01): 248-258.

张旸, 周成虎, 戴锦芳, 等. 2004. 偏最小二乘回归方法在土地利用结构研究中的应用[J]. 自然资源学报, 19(6): 804-810.