基于递归分析的齿轮故障识别方法
曹 亭,赵华东,邓 东
( 1.西安石油大学,陕西 西安 710065; 2.西北大学,陕西 西安 710069)
0 引 言
石化装置负载大、工况恶劣,且运行周期长,其传动系统以齿轮传动为主,因此齿轮箱在生产中运行的好坏直接影响到石化生产的平稳和安全[1]。据统计,传动机械故障中齿轮箱故障约占 10.3%,而齿轮箱的各种零件中故障率最大的是齿轮,统计其故障率超过60%[2]。现今石化企业对装备的维护普遍采用实时维护制度,为实现精益管理,实时监控设备并进行故障预识别将成为一种必然趋势,对石化装置的维护维修和长周期安全运行有重要意义。振动检测是进行监测和诊断的主要手段,研究表明齿轮振动信号具有非线性及非平稳的特性[3],这是因为在数据采集时有许多无法避免的噪声。提取齿轮故障信号特征信息的方法有很多,包括时域波形法、时域参数分析法、频谱分析法等传统分析方法,但是这些分析法受齿轮振动信号的非线性及非平稳特性的影响很大,并且需要预先了解故障的机理,才可以精确的识别故障类型。递归图是Eckmann等人提出的一种基于相空间重构的,能直观的表现非线性系统动力学特性的描述方法,可以定性的分析出系统在相空间中的行为。递归图及递归定量分析在故障识别中已经有了初步的运用,但很少有人将该方法运用到齿轮的故障识别中。通过实验提取正常、断齿、裂纹和剥落四种情况下的齿轮振动时间序列,利用相空间重构分别构造了与原动力系统在拓扑意义下对应的等价相空间。然后,在用递归图对齿轮振动信号时间序列进行分析的基础上,采用递归定量分析提取递归图的图像特征来识别齿轮的故障类型,并与传统的频谱分析结果对比验证此方法的准确性。
1 相空间重构
相空间重构是运用递归图法的必要步骤,相空间重构的好坏更直接影响到递归图的质量。该方法的关键是构造一个非线性时间序列的嵌入,选择合适的延迟时间τ和嵌入维数m。Ruelle在1981年提出离散时间序列的时间延迟法[4]。其本质是通过一维离散的时间序列{x(ti)}(时间间隔为Δt)和它的时间延迟X(ti)来构造m维相空间矢量:
X(ti)= {x(ti+τ),x(ti+2τ),…,x(ti+
(m-1)τ)}X(ti)={x(ti+τ),x(ti+
2τ),…,x(ti+(m-1)τ)}
(1)
式中:τ为延迟时间,取为Δt的整数倍,这里取τ=1Δt。
但是,坐标延迟相空间重构技术的关键是,嵌入维数m和延迟时间τ的确定。Takens定理中,对于理想的无限长和无噪声的一维时间序列,嵌入维数m和延迟时间τ可以取任意值,但实际应用中的时间序列都是有限长度且存在噪声,嵌入维数m与延迟时间τ必须选择恰当,才能重现原系统的动力特性,否则会极大地影响重构的相空间的质量。1999年,H.s.Kim、R.Eykholt和J.D.Salas提出了C-C算法,该方法结合了自相关函数和互信息方法的优点,既可以有效减少计算量,又能保持系统的非线性特征。采用改进后的C-C算法[5]并编写Matlab程序,运用关联窗同时估计出延迟时间τ和嵌入窗τw。G-P算法是由Grassberger 和Procaccia提出的饱和关联维数法[6],用于从时间序列中提取信息。G-P是求解嵌入维数m的一种最常用的算法[7]。编写Matlab程序,通过给定合适的步长r,求解关联积分C(r),再利用lnC(r)和lnr之间关系的线性回归图来确定最佳的嵌入维数m。
2 递归图原理
1987年,Eck-mann等人将相空间重构理论与递归概念相结合,提出了递归图方法[8]。递归图可以将重构的高维相空间的时间序列递归特征展现在二维平面中,实现系统动力学特性的可视化。其算法简述如下:
将一维的离散时间序列x(ti)(i=1,2,…,N)通过相空间重构为一个m维的相空间。
(2)
式中:x(ti)为m维空间的第i个相点矢量;m为嵌入维数;τ为延迟时间。
将以上重构的相空间转化为递归图,需要进行以下步骤:
(1) 确定递归图中的点
(3)
式中:ε为给定的阈值常数;‖·‖为向量范数,通常可用的范数包括1范数、2范数和∞范数,每种范数对应的邻域形状不同,在给定的阈值常数ε下,由于∞范数对应的邻域最大且计算最为简单,因此采用∞范数;Θ(•)为Heaviside函数:
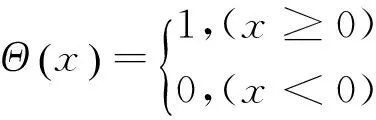
(4)
(2) 作图
分别以i,j为横纵坐标,Ri,j为函数值,作出的二维平面图即得到递归图。由式(3)可知,矩阵Ri,j由0和1组成,当相空间两个相点距离在阈值ε内为1,显示为黑点,反之则为0,显示为白点。最终构成的黑白二值图像中存在一条主对角线,若其余像素点均布其余平面,信号为平稳随机信号;若存在与主对角线平行的规则像素带,则表明该信号具有某种周期特性[9]。
3 齿轮振动信号递归分析
采集齿轮的振动信号后,先重构相空间,再在重构的高维相空间中提取时间序列的递归特性,构建齿轮振动信号的递归图。
3.1 振动信号的采集
预制了正常、剥落、裂纹和断齿4种状态的齿轮,通过实验采集了它们振动信号,采集参数如表1所列。对四组齿轮振动的时域信号作傅里叶变换,得到各信号的幅值频谱如图1所示。从图1可以看出,正常组的幅值最大值为10,且没有较大的峰值出现。剥落组的幅值最大值为25,且出现了峰值的集中段。裂纹组的幅值最大值为40,在啮合频率、啮合频率倍频及各阶谐频范围内,振动幅度明显增大。断齿组的幅值最大值为40,在转频、啮合频率以及啮合频率的倍频处幅度显著增大。通过对4种状态齿轮的频谱对比分析发现,频谱分析可以发现故障是否存在,但由于频率分辨率的限制,无法确定转动频率和啮合频率,使得识别故障的具体类型困难很大。
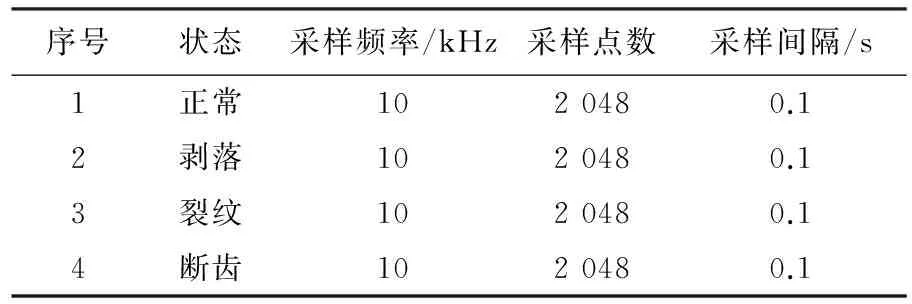
表1 齿轮振动信号采集参数

图1 齿轮各状态幅频图
3.2 齿轮振动信号的递归图
将采集的齿轮振动信号导入Matlab程序中,计算出S(t),ΔS(t),Scor(t)三个函数值,并通过函数图像找出最佳的延迟时间τ。再根据延迟时间τ,结合G_P算法的Matlab程序,计算出嵌入维数m。结果如表2所列。

表2 延迟时间与嵌入维数表
对采集的振动信号振动信号进行递归分析,得到4组递归图,如图2所示。

图2 齿轮各状态递归图
由图2可知,4种状态的递归图中均以垂直和水平分布的递归点,即纵横层状结构为主,这表明齿轮振动信号成份较复杂[10]。显然,4幅递归图中递归点分布存在很大差异:当齿轮为正常状态时,层状结构相对稀疏,递归点分布较均匀,说明信号中白噪声均匀分布,没有异常的频率成份。剥落状态下,递归点相对集中,在左上角形成了1个面积较大的集中域,这表明由剥落引起的特别状态时间增长从而使得信号中出现异常频率。裂纹状态下,递归图中出现了纵横分别三条白点集中区域,层状结构较突出。断齿状态下,集中区域为纵横两条白点集中区域,相比裂纹状态下递归点更集中,层状结构则更加突出,更容易识别。
对比分析图1与图2发现,递归图与传统的频谱分析方法不同,它不受振动信号的环境白噪声影响,不同的齿轮状态的递归图特征之间差别明显,能更直观清楚的展现齿轮的状态。
4 结 论
基于递归图编写了Matlab程序,对正常、剥落、裂纹和断齿四种状态的齿轮振动信号进行分析。
分析结果表明不同齿轮状态的递归图特征存在明显的差异,主要体现在递归点的个数和分布规律上,表现为集中区域和层状结构的位置、大小不同。与传统的频谱分析法对比结果说明递归图是识别齿轮故障的一种有效方法。
参考文献:
[1] 何照荣,孙志伟, 宣征南,等.基于油液分析技术的石化挤压机减速箱故障诊断应用[J].石油化工设备技术,2016,37(1):15-18.
[2] 郭福平,李 谷.基于HHT的齿轮故障声发射实验研究[J]. 化工机械,2017(4):390-393.
[3] 吕 勇,李友荣,徐金梧.延时矢量方差算法及其在齿轮故障识别中的应用[J].振动与冲击,2006,(25)6:59-61.
[4] 石博强,申焱华.机械故障诊断的分形方法:理论与实践[M].北京:冶金工业出版社,2001.
[5] 胡 瑜,陈 涛.基于C-C算法的混沌吸引子的相空间重构技术[J]. 电子测量与仪器学报,2012(5):425-430.
[6] 高俊杰,王 豪.基于改进的G-P算法的相空间嵌入维数选择[J]. 计算机工程与应用,2014(9):107-110.
[7] 吕 威,王和勇,姚正安,等.改进嵌入维数和时间延迟计算的GP预测算法[J]. 计算机科学,2009(5):187-190.
[8] Marwan N, Thiel M, Nowaczyk N R. Cross recurrence plot based synchronization of time series [J]. Nonlinear. Proc. Geophys, 2002(9):325-331.
[9] Men Jian, Qu Liangshen. Recurrence plot-A new method for the evaluation of mechanical state complexity [J]. Dynamic Analysis and Measurement Technique,1997,15(3):30-35.
[10] 肖 涵,吕 勇.齿轮振动信号滑动递归分析及其应用[J].机械传动,2015(3):31-35.

