基于热-结构耦合的圆柱齿轮副修形分析
田文昌,林腾蛟,汪 彤
(1.重庆大学 机械传动国家重点实验室,重庆 400044; 2.重庆齿轮箱有限责任公司,重庆 402263)
0 引 言
齿轮装置在传递功率时,承受载荷和温度的作用,各零部件都会产生不同程度的变形,导致齿轮齿形的畸变,使齿轮在啮合过程中产生冲击、振动和偏载,从而使得齿轮早期失效的概率增大。因此需要对齿轮副齿形进行适当的修整,改善其运转性能,以提高承载能力、延长使用寿命。
国内外很多学者对齿轮温度场和修形问题进行了大量研究,并取得了丰富的研究成果。Cheng和Patri等人提出把轮齿本体温度问题作为稳态温度场问题处理,建立有限元分析模型,得到了符合工程要求的结果[1-2];张言羊等研究了直齿圆柱齿轮的本体温度场,并计算了轮齿的热变形,得出当载荷沿齿宽分布不均匀时,热变形有可能导致热弹失稳的结论[3];Miad Yazdani等人通过对齿轮箱的热流耦合分析,提出了齿轮箱温度的预测模型,并通过试验进行了对比分析[4];袁野、汤海川等指出齿轮副修形可以减小齿轮啮合干涉,降低齿轮噪声[5-6];陈思雨、唐进元、朱才朝等研究了轮齿修形对齿轮箱动态特性的影响,指出齿轮修形能降低齿轮箱振动加速度、时域冲击、振动烈度等动态指标[7-8];姚阳迪等研制了齿轮温度场即热弹变形计算软件,为齿轮修形提供了方便快捷的技术手段[9];郝东升等以齿面应力分布均匀为主要目标,迭代求解修形齿轮应力分布,优化了齿轮修形参数[10]。
以上文献通过理论和实验研究了齿轮修形的作用,但多集中于修形对齿轮箱动态特性的改善,关于本体温度对修形量的影响以及修形后齿轮副本体温度分布变化的研究相对较少。基于齿轮箱喷油润滑热流耦合分析,计算了齿面对流换热系数,利用ANSYS数值模拟仿真,计算了齿轮副本体温度分布状况,进而建立热-结构耦合分析模型,计算了齿轮副修形量,并对比分析了修形前后齿轮副齿面压力、热流密度和本体温度分布状况。
1 齿轮本体温度场分析
1.1 对流换热系数计算
此前齿轮副对流换热系数的确定一般通过简化公式计算,但由于润滑条件复杂、啮合面润滑油分布状况不确定等原因,导致计算结果误差较大。通过热流耦合喷油润滑仿真分析,考虑实际运行工况下润滑油分布状况,得出与实际情况较为接近的齿轮副对流换热系数。
1.1.1齿轮箱内部流场仿真模型
齿轮副的参数如表1所示,齿轮箱结构如图1所示。带喷油孔的齿轮箱建模过程为:将齿轮箱几何模型导入前处理软件ICEM-CFD中,建立润滑油流动空间,并对流体区域划分四面体网格,其中在齿面附近区域和喷油口处采用局部加密的方法建立流场计算模型,提高计算精度。计算模型共计795 487个四面体网格单元[11]。
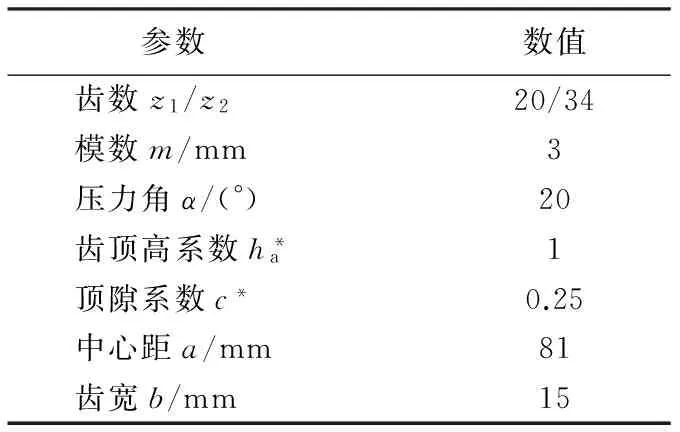
表1 齿轮副基本几何参数
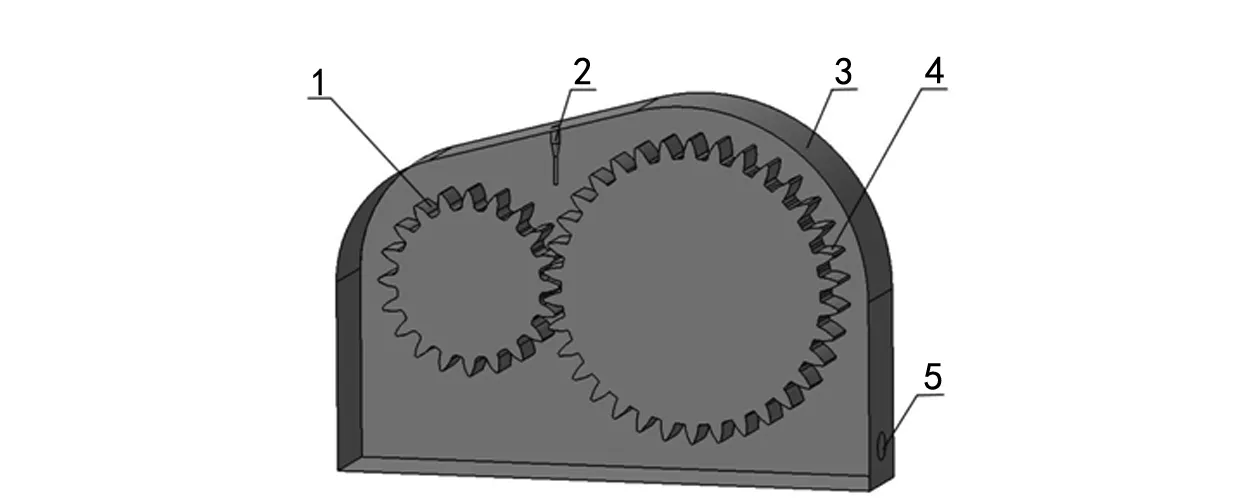
图1 齿轮箱内部结构1.主动轮 2.喷油嘴 3.齿轮箱 4.从动轮 5.出油口
将前处理后的模型导入Fluent中进行求解。采用VOF两相流模型:初相为空气,密度为1.225 kg/m3,动力黏度为1.789 4×10-5kg/(m·s),比热容为1 006.43 J/kg·K,热导率为0.024 2 W/m·K;次相为润滑油,密度为970.0 kg/m3,动力黏度为2.4×10-2kg/(m·s),比热容为2 230 J/kg·K,热导率为0.149 W/m·K。主动顺时针旋转,转速为6 120 r/min;从动轮逆时针旋转,转速为3 600 r/min;齿轮箱壁面和齿轮表面为无滑移固壁,齿轮的转动通过设置动网格实现;喷油口喷油流量为0.75 L/min。
1.1.2齿轮箱内部热流耦合仿真分析结果
图2给出了齿轮箱内部润滑油分布均匀后齿轮副表面对流换热系数分布情况。提取齿轮副各表面对流换热系数值,并取其一个啮合周期内的平均值,得到主动轮齿面对流换热系数为3 860 W/(m2·℃),轮齿端面对流换热系数560 W/(m2·℃),轮毂对流换热系数240 W/(m2·℃);从动轮齿面对流换热系数为3 250 W/(m2·℃),轮齿端面对流换热系数430 W/(m2·℃),轮毂对流换热系数220 W/(m2·℃)。

图2 齿轮副对流换热系数分布
1.2 热流密度计算
高速运转条件下啮合齿对间的相对滑动产生大量摩擦热,热流密度由齿面接触压力、相对滑动速度和齿面的摩擦系数共同确定。在接触区域,热流密度可表示为:
Q=P·vs·f
(1)
式中:P为啮合点处接触压力;vs为啮合点处主、从动轮相对滑动速度;f为啮合点处摩擦系数。
1.2.1接触压力计算
齿轮副有限元模型如图3所示,共有202 176个单元,248 402个节点。对齿轮副施加载荷和约束边界条件,进行有限元加载接触分析,将单对轮齿从啮入到啮出的整个过程分成120个啮合位置计算,每个位置小齿轮转动0.3°,确定齿轮副各接触位置压力值。通过ANSYS APDL语言编写后处理程序,提取接触区域内各单元接触压力,得到沿齿高方向接触压力变化曲线如图4所示。

图3 齿轮副有限元分析模型 图4 沿齿高方向接触压力变化曲线
1.2.2齿面相对滑动速度计算
主、从动齿轮的啮合齿对在接触面切线方向上的绝对速度是不同的,导致了主、从动齿轮齿面的相对滑动;但主、从动齿轮的啮合齿对在接触面法线方向上的绝对速度是相等的,因而保证了轮齿啮合过程中等速运动的传递。图5给出了齿轮副相对滑动速度计算示意图。
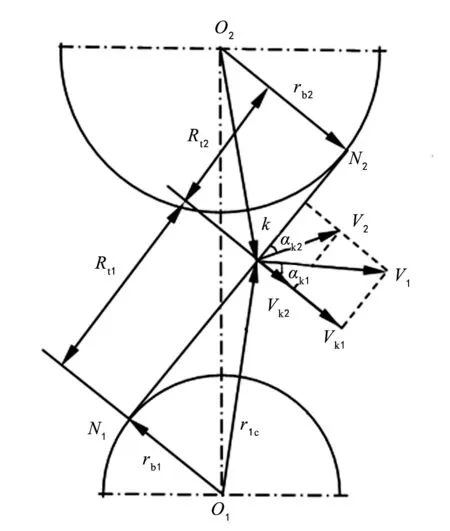
图5 齿轮副相对滑动速度计算示意图
主、从动齿轮接触点k沿接触切线方向上的绝对速度Vk1和Vk2可表示为:
Vk1=ω1×O1k×sinαk1=ω1×kN1
(2)
Vk2=ω2×O2k×sinαk2=ω2×kN2
(3)
两齿轮的相对滑动速度Vkk可表示为:
(4)
式中:ω1、ω2分别为主、从动轮转速;N1N2为齿轮副啮合线;i为齿轮副传动比。
1.2.3齿面摩擦系数计算
齿面摩擦系数随转速和载荷的变化而改变,并且受轮齿啮合位置、齿面粗糙度、润滑油动力粘度以及齿轮平均温度的影响。对于齿轮齿面任意啮合位置k,摩擦系数μk可由以下公式表示[12]:
(5)
式中:Ftk为齿轮的切向载荷;b为齿宽;αt为端面压力角;RE为综合曲率半径;XR为粗糙度因子;η为润滑油动力粘度系数。
综合上述,可得到齿轮副啮合面上沿齿高方向热流密度分布状况如图6所示。

图6 修形前齿轮副热流密度分布曲线
1.3 本体温度场分析
在本体温度场分析中,各接触点的热流密度为定常值,即总热流量在整个啮合过程中的平均值,将啮合区域各节点热流密度加载在轮齿对应位置,如图7所示。
将热流耦合分析计算得到的对流换热系数施加于齿轮副各表面,如图8所示;实际工作时为了保证润滑油动力粘度处于合适范围,一般会将其加热到一定温度再输入齿轮箱,此处将环境温度设置为80 ℃。
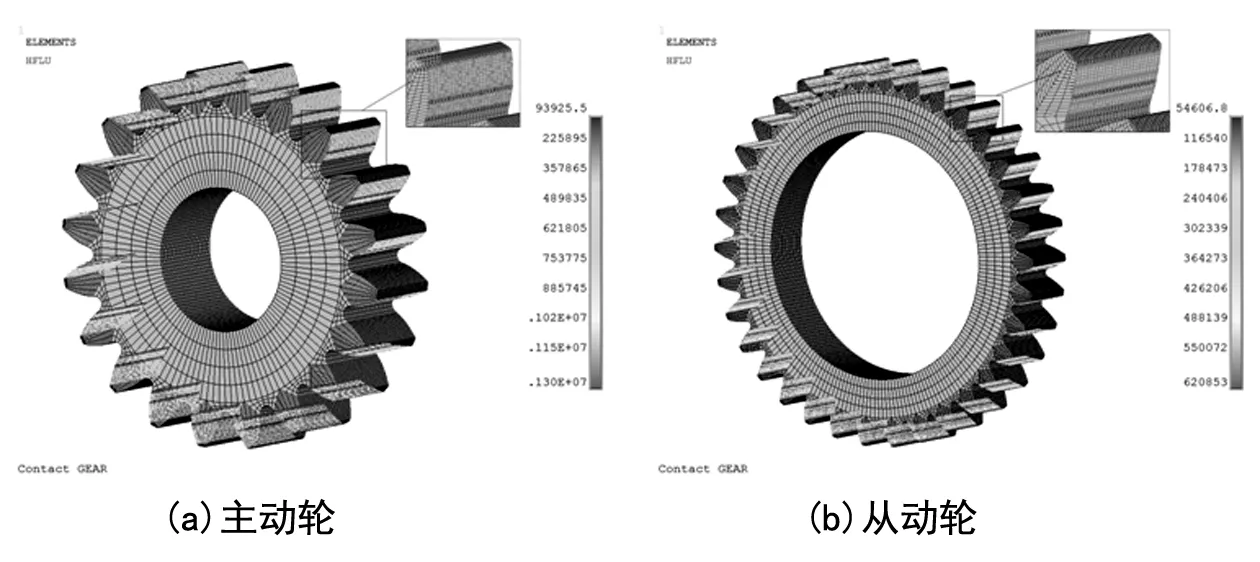
图7 齿轮副热流密度加载
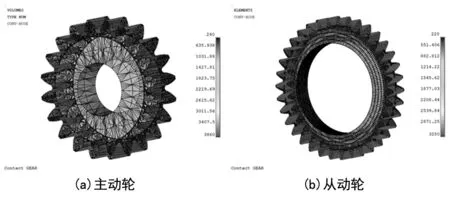
图8 齿轮副表面对流换热系数
计算得到齿轮副稳态本体温度场分布结果,如图9所示。主动轮温度分布在103~117 ℃之间,最高温度位于靠近齿根处;从动轮温度分布在96~107 ℃之间,最高温度位于靠近齿顶处。由于从动轮啮合次数与主动轮相比较少,因此相同啮合时间内,从动轮各轮齿输入热流量较小,本体温度也相对较低。主、从动轮沿齿高方向各节点温度变化曲线,如图10所示。
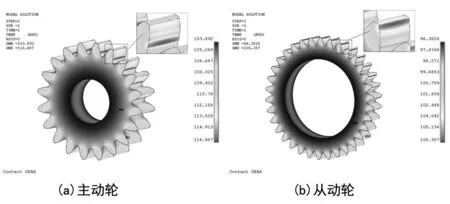
图9 齿轮副稳态本体温度场分布

图10 修形前齿轮副本体温度分布曲线
2 齿轮副修形量计算
2.1 热-结构耦合修形分析
轮齿修形原理如图11所示,由于轮齿误差和变形产生啮合基节误差,从而使齿轮副形成啮入/啮出干涉,最大修形量由啮入、啮出位置主、从动轮基节之差确定。对齿轮副进行热弹耦合分析,其中啮入/啮出齿不添加接触对,得到各齿轮副啮入干涉变形、啮出干涉变形量,即齿轮副啮入、啮出最大修形量。

图11 齿轮副修形原理
将齿轮副旋转至啮入和啮出位置分别进行热-结构耦合分析,计算模型与之前温度场分析模型相同,同时设置材料热膨胀系数为1.26×10-5/℃,初始膨胀温度为20 ℃;对齿轮副施加约束边界和载荷边界,同时读入本体温度场结果文件作为热边界。图12和图13分别给出了啮入、啮出位置的位移云图和接触应力云图,其中啮入位置最大综合位移为0.017 mm,最大接触应力为727 MPa;啮出位置最大综合位移为0.013 mm,最大接触应力为749 MPa。
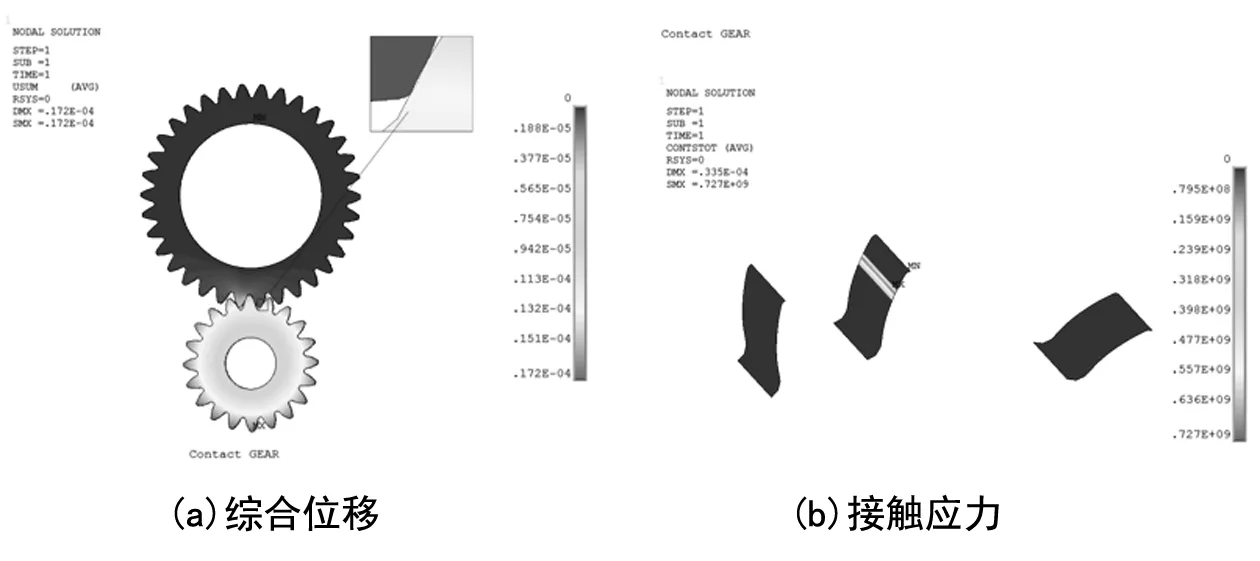
图12 啮入位置热-结构耦合分析结果
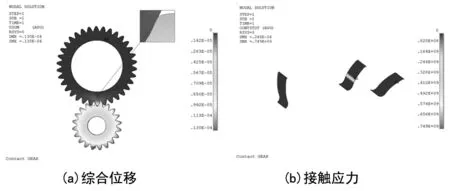
图13 啮出位置热-结构耦合分析结果
2.2 修形量计算
修形量由相对位移确定,求解得到的齿轮绝对位移结果需减去刚体位移。其计算公式如下[13]:
啮入位置修形量为:
Δamax=Δf2-Δf1
(6)
啮出位置修形量为:
Δrmax=Δf1-Δf2
(7)
主、从动齿轮啮合基节变化量为:
Δfi=±[(δci-θsircicosθci)-(δei-θsireicosθei)]
(8)
式中:正负号取啮入位置为正、啮出位置为负;下标1、2代表主、从动轮;δci、δei为主、从动轮相邻齿啮合点与啮入、啮出点位移;rei为主、从动轮啮入或啮出点半径;rci为齿轮副处于啮入或啮出位置时相邻啮合点半径;θsi为主、从动轮刚体转角;θei为啮入或啮出位置主、从动轮啮出点压力角;θci为齿轮副处于啮入或啮出位置时相邻啮合点压力角。
3 齿轮副修形效果分析
未修形齿轮副由于弹性变形和热变形引起主、从动轮轮齿发生变形,使啮合初始点发生干涉现象,从动轮齿顶产生应力集中,齿顶啮合区域压力增大,并且由于单双齿交替啮合的原因,轮齿在啮合过程中载荷分布有明显突变现象。
通过修形将啮合齿对上发生干涉的齿面部分削去,齿轮副在初始啮合点刚好接触,在初始啮合位置齿面压力降为零,然后逐渐增加,直到进入单齿啮合区;在啮出阶段,由于主动轮齿顶部分也进行了相应修正,齿面压力也逐渐减小。齿轮修形消除了轮齿啮合过程中载荷的突变现象,降低了齿轮损坏几率,提高齿轮副使用可靠性。修形前后齿轮副沿齿高方向齿面压力分布对比曲线如图14所示。

图14 修形前后齿面压力分布曲线
修形前齿轮副啮入、啮出区相对滑动速度较大,并且由于啮入干涉的影响,齿面压力同样较大,导致齿轮副齿根和齿顶部分热流密度偏大;修形后,啮入啮出区压力变小,齿顶和齿根部位热流密度变小,齿面热流密度分布状况改变,修形前后齿面热流密度分布对比曲线如图15所示。由于修去了齿顶附近的渐开线部分,齿根和齿顶附近啮合区所受载荷较小,相对滑动速度较大的部分产热量大幅度减小,因而齿轮副摩擦损失和温升降低。修形前后齿轮副主、从动轮沿齿高方向温度分布对比曲线如图16所示。
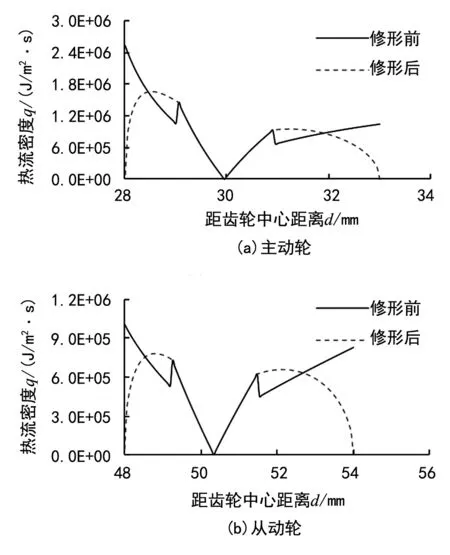
图15 修形前后齿轮副热流密度分布曲线
4 结 论
(1) 建立了高速齿轮箱喷油润滑热流耦合分析模型,得到齿轮箱内部润滑油分布均匀后齿轮副表面对流换热系数分布情况。
(2) 利用有限元分析得到齿轮副本体温度分布状况,通过热-结构耦合分析得到齿轮副修形量。
(3) 对比分析修形前后齿面压力、热流密度以及本体温度分布状况,得出修形后齿面压力分布状况改善,消除了轮齿啮合过程中载荷突变的现象,啮入和啮出区域热流密度大幅度减小,齿轮副摩擦损失和温升减小,本体温度降低。
参考文献:
[1] Nadir Patir, Cheng H S. Prediction of the bulk temperature in spur gears based on finite element temperature analysis[J]. Tribology Transactions,1979,22(1):25-36.
[2] Wang K L, Cheng H S. A numerical solution to the dynamic load, film thickness, and surface temperatures in spur gears, part II: Results[J].Journal of Mechanical Design,1981,103(1):188-194.
[3] 张言羊,刘正平.直齿圆柱齿轮三维本体温度场和热变形的研究[J]. 西安交通大学学报,1990,24(4):25-30.
[4] Yazdani M, Soteriou M C, Sun F, et al. Prediction of the thermo-fluids of gearbox systems[J]. International Journal of Heat and Mass Transfer, 2015(81):337-346.
[5] 袁 野.齿轮噪声与齿轮修形[J].机械研究与应用,2006,19(5):7-8.
[6] 汤海川,郭 枫.基于齿轮修形的汽车变速器齿轮啸叫噪声改善研究[J].上海理工大学学报,2013,35(3):294-298.
[7] 陈思雨,唐进元,王志伟,等.修形对齿轮系统动力学特性的影响[J].机械工程学报,2014,50(13):59-65.
[8] 朱才朝,陈 爽,马 飞,等.轮齿修形对兆瓦级风电齿轮箱动态特性影响[J].振动与冲击,2013,32(7):123-128.
[9] 姚阳迪.基于热弹变形的高速重载齿轮修形研究[D].重庆:重庆大学,2010.
[10] 郝东升,董惠敏,毛范海,等.直齿行星传动齿轮修形优化设计方法[J].大连理工大学学报,2012,52(5):657-663.
[11] 曹 寓,林腾蛟,田文昌.基于动网格的齿轮喷油润滑流场仿真分析[J].机械研究与应用,2017,30(3):18-22.
[12] Handschuh R F, Kicher T P. A method for thermal analysis of spiral bevel gears[J].Journal of Mechanical Design, 1996, 118(4): 580-585.
[13] 杨欣茹,林腾蛟,何泽银.考虑轴线平行度误差及热变形的齿轮修形设计[J].机械传动,2016,40(10):74-79.

