加速度对半球谐振陀螺控制系统影响分析及抑制方法
徐泽远,伊国兴,谢阳光,魏振楠
(1. 哈尔滨工业大学空间控制与惯性技术研究中心,哈尔滨 150001;2. 中国航空工业集团公司西安自动飞行控制研究所,西安 710065)
半球谐振陀螺由于具有高精度、高可靠性、抗干扰能力强以及长寿命的优点,非常适合应用在长时间工作的场合[1-2]。因此,高精度半球谐振陀螺的研究对于惯性技术的发展,特别是长寿命高精度陀螺的发展是尤为重要的。半球谐振陀螺有很多应用,比如用于航空导航、卫星导航定位、精密定位、石油勘探、深海探测等等。作为载体导航系统的重要惯性元器件之一,半球谐振陀螺的性能将直接影响惯性导航系统的性能,甚至影响载体的性能和使用。所以研究哪些因素影响半球谐振陀螺的性能和精度具有重要意义。
对于半球谐振陀螺的研究,主要集中在它的随机误差[3-5]、温度漂移[6-7]、有限元分析[8]和寿命预测[9]等方面。而在陀螺的实际应用中,环境因素的影响也是不容忽略的,如温度场、磁场、外载荷等,其中外载荷中重力加速度以及载体运动加速度不可避免地作用到陀螺本身[10],实际测试结果表明,这样亦能使陀螺产生漂移。而半球谐振陀螺是一种高精度陀螺,所以对于加速度造成的影响是不能被忽略的。近几年,越来越多的研究集中在半球谐振陀螺的控制方式上,这些控制方式又很难去实现,甚至会带来新的更为复杂的问题,而半球谐振陀螺的振幅和速率控制系统会直接影响到陀螺精度。加速度对于半球谐振陀螺性能的影响可以直接反映在陀螺内部的振幅控制系统和速率控制系统上,为此开展加速度对半球谐振陀螺控制系统的影响分析具有十分重要的实际应用价值。
半球谐振陀螺主要是通过控制系统的激励电极施加电压使谐振子谐振起来达到其固有频率。从动力学的角度分析,外界加速度的作用下会使得谐振子产生变形,与正常工作的谐振子形变相比,这是有害变形。加速度造成的变形会使得谐振子与外基座激励电极的相对位置发生变化,这就使得谐振子的电极板与激励电极的电极板之间的相对位置和相对距离产生变化,使得激振力和反馈力产生偏差,从而造成振幅和速率激励电极的控制电压误差,由此带来陀螺输出的漂移。为此本文分析了加速度对振幅控制系统和速率控制系统的影响。
1 谐振子的变形方程
在建模过程中,将中面半径为R、厚度为h的伞形的谐振子结构简化为半球形进行建模,则半球谐振子上电极的边界方向θ和φ构成中面的主坐标系,如图1所示。取激励电极面积范围内任意一点B,直线OB与变形后的谐振子中面相交于点A´,此处OB=Rf,假设OA´=Rd,则电容间隙表达式为[10]:
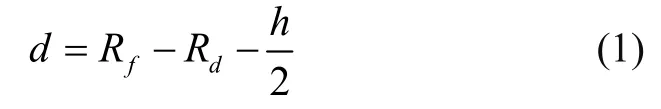
为求出式(1)中Rd,需要了解谐振子变形后的曲面方程。谐振子中面上物质点A变形后,移动到A´点,则点A´对应的位移矢量q′与点A对应的位移矢量q和变形矢量W的关系如图1所示。
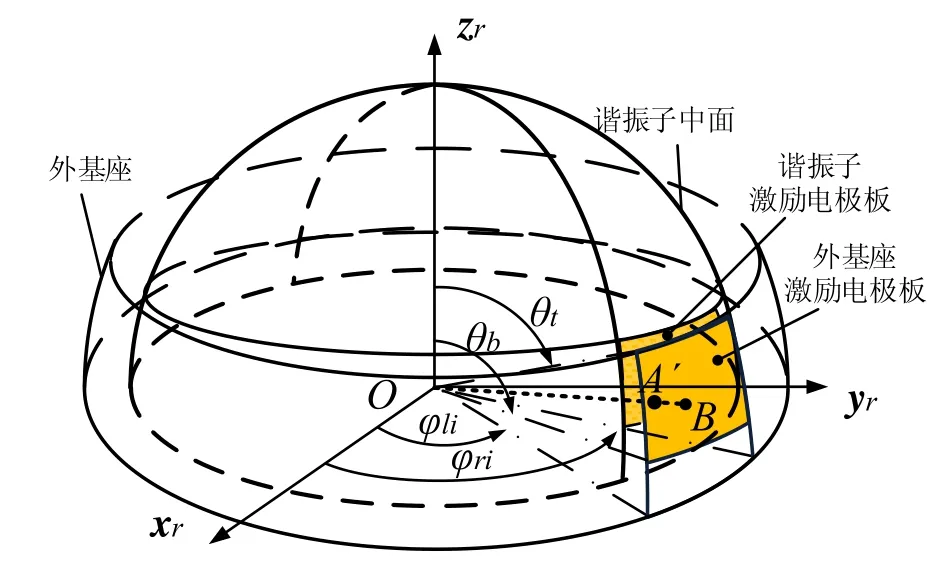
图1 激励电极结构图Fig.1 Structure diagram of the actuator
直线与谐振子中面相交满足如下方程[10]:


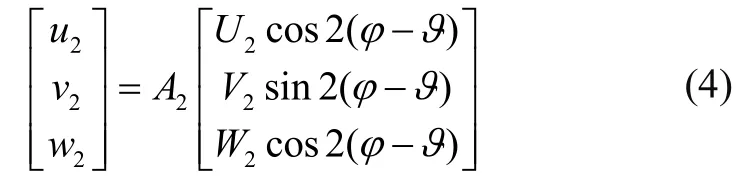
式中:A2为振幅,ϑ为振型角[10],U2、V2、W2振型方程为瑞利-里茨函数,其中,
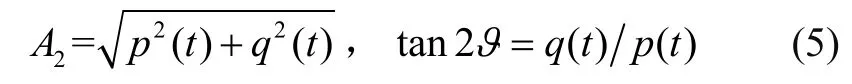
式中,p(t)、q(t)为与时间相关的待定量。
加速度作用下谐振子变形方程形式如下[10]:

式中:A1为加速度作用下谐振子变形幅值,ψ为加速度作用的方位,U1、V1、W1为瑞利函数。瑞利里茨函数通用形式如下:
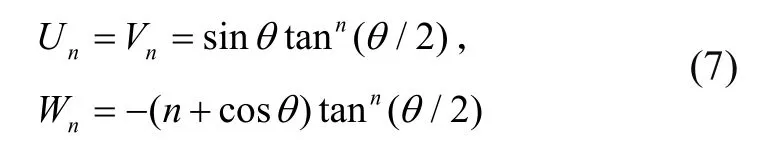
2 振幅和速率反馈控制系统
2.1 控制系统结构
外基座上均匀分布的 16个激励电极,间隔为22.5°,如图2所示。此处用于振幅控制的激励电极有4个,用于速率反馈的激励电极有4个,其余8个电极用于频率控制和正交控制。根据谐振子二阶谐振状态的对称性,组建振幅、速率反馈控制系统。结合实际工程设计,8个激励电极的双差分方式结构复杂[10],在加工制造上会带来很多问题,在工程实践上不具有可行性,由此设计了以下三种控制方式:
1)将0°激励电极F1作为振幅激励电极,与0°检测电极P1共同构成了振幅反馈控制系统;将45°激励电极F2作为速率激励电极,与45°检测电极P2共同构成了速率反馈控制系统。如图2所示。这是最基本的振幅和速率反馈控制系统。
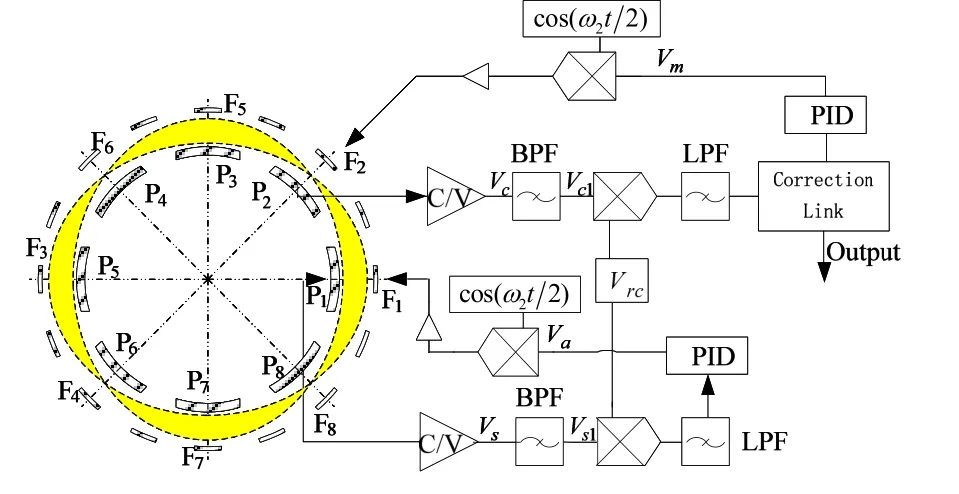
图2 反馈控制系统控制方式IFig.2 Scheme I of feedback control system
2)将F1、F5信号差分作为振幅激励电极,将P1、P3信号差分作为振幅检测电极,共同构成了振幅反馈控制系统;将激励电极F2、F6信号差分作为速率激励电极,将P2、P4信号差分作为振型角检测电极,共同构成了速率反馈控制系统。如3图所示。

图3 反馈控制系统控制方式IIFig.3 Scheme II of feedback control system
3)将激励电极 F1、F3并联作为振幅激励电极,将P1、P5并联作为振幅检测电极,共同构成了振幅反馈控制系统;将激励电极F2、F4并联作为速率控制电极,将P2、P6并联作为振型角检测电极,共同构成了速率反馈控制系统。如4图所示。

图4 反馈控制系统控制方式IIIFig.4 Scheme III of feedback control system
2.2 多电极激励谐振子的动力学特性
由谐振子的变形方程解析解形式已知,建立了多激励电极作用下谐振子的动力学方程:
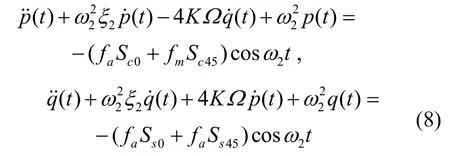
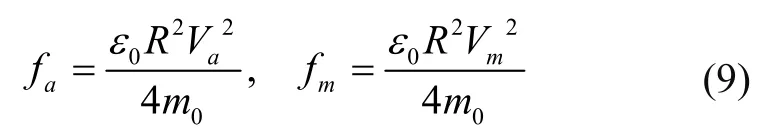
其中,0ε为真空介电常数,动力学参数m0=-0.0027。

当谐振子进入二阶谐振稳定状态时,
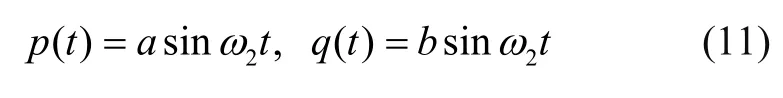
其中,2ω为谐振子二阶谐振频率,t为时间。
当采用控制方式I时,

当采用控制方式II时,

当采用控制方式III时,
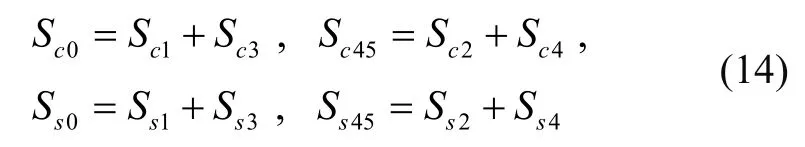
进一步,

为进一步讨论控制特性,以方案I为例进行说明,当表头不存在结构误差时,将表1中数据代入式(16)得:

从式(18)可以看出,通过调整fm、fa的比值可以使ϑ= 0 ,此时式(15)中b=0,式(15)化简为
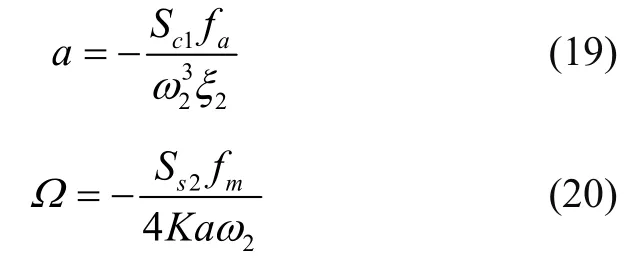
当谐振子振型角被锁定在零位时,式(19)(20)代表了振幅控制及速率控制系统的规律。可以看出,两个控制系统没有耦合,但实际上两个系统是存在耦合的。
3 加速度对激励电极的影响分析
3.1 误差分析
在陀螺正常工作状态,振幅控制及速率控制保证了a=constant,b=0,此时式(15)简化为

进一步推导:
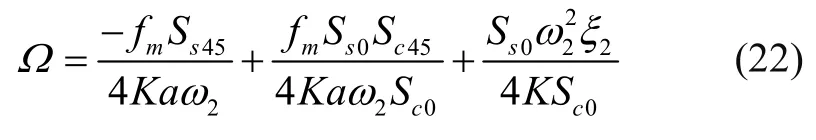
也可推导成:
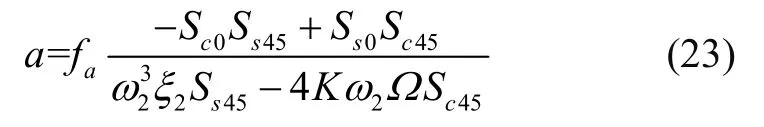
对比式(20)与式(22)可以发现,激励系数Sc0、Ss0、Sc45、Ss45会导致陀螺常值漂移及标度因数误差。对比式(19)与式(23)可以看出,Sc0、Ss0、Sc45、Ss45会影响振幅激励电极的控制精度,导致振幅的漂移。
在加速度作用下,谐振子与外基座的激励电极发生相对位移,使得式(10)中积分域θ、φ以及初始电容间隙d的变化导致激励系数Sc0、Ss0、Sc45、Ss45发生改变,产生陀螺角速率常值漂移和振幅漂移以及标度因数误差。由式(1)(3)(10)可以看出,分析加速度对振幅、速率控制系统的影响就是分析加速度参数1A、ψ与激励系数Sc0、Ss0、Sc45、Ss45的对应关系。
采用数值分析计算的方法建立仿真系统,研究加速度导致的激励电极误差,仿真参数设置如表1所示。

表1 仿真参数Tab.1 Simulation parameters
3.2 振幅控制系统误差
首先研究了加速度导致激励系数的改变,激励系数的改变直接导致了振幅控制因数误差,根据力反馈陀螺工作原理,振幅控制电压的改变表现为振幅的漂移。从式(23)可以看出,fa是与电压有关的变量,而其它量都是受加速度影响的量,定义为振幅控制因数式(19)中的系数定义为Kac0,振幅控制因数误差率为 δKac。
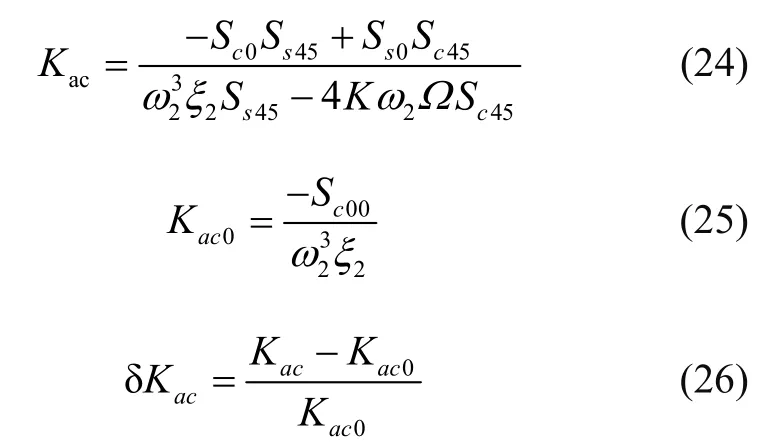
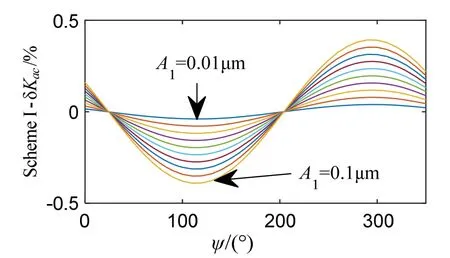
图5 控制方式I振幅控制因数误差率Fig.5 Amplitude control factor error rate of scheme I
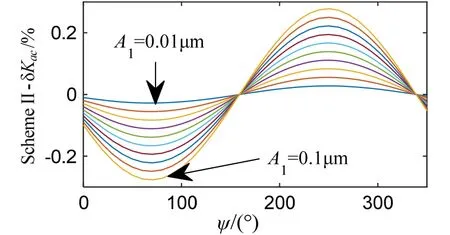
图6 控制方式II振幅控制因数误差率Fig.6 Amplitude control factor error rate of scheme II

图7 控制方式III振幅控制因数误差率Fig.7 Amplitude control factor error rate of scheme III
解算出振幅控制因数,将其与谐振子未变形时的理想值对比即可得到控制方式I、II、III的振幅控制因数误差率。
从图5~7中可以看出,控制方式I的振幅控制因数误差率最大为 0.3926%。这是最基本的控制方式,控制精度比较低,但是加速度引起的振幅控制误差不到 4‰。控制方式 II的振幅控制因数误差率为0.2779%。控制方式 III的振幅控制因数误差率为6.692×10-4%。从以上三种控制方式的仿真结果来看,控制方式 III中加速度引起的振幅激励电极误差几乎为零,选用控制方式III则认为加速度对振幅控制系统没有影响。可以认为,谐振子的振幅是稳定的。
3.3 速率控制系统误差
加速度导致激励系数的改变,激励系数的改变导致了速率控制因数改变,根据力反馈陀螺工作原理,控制电压改变,表现为输出角速率的漂移。
从式(22)可以看出,fm是与电压有关的变量,而其它量都是受加速度影响的量,定义为速率控制因数速率控制因数误差率δKrc、耦合因数Kcf、耦合因数误差率δKcf、角速率输出常值误差Kce。式(20)中的系数定义为Krc0。

解算出加速度作用下的速率控制因数、耦合因数、常值误差,将其与谐振子未变形时的理想值对比即可得到控制方式I、II、III的速率控制因数误差率、耦合因数误差率、常值误差。
从图8可以看出,控制方式I的速率激励电极控制因数误差率最大达到11.14%,说明加速度对陀螺速率激励电极影响较大。而耦合控制因数误差率最大为4.17×10-6%,加速度导致的控制系统间的耦合误差较小,可以忽略不计。加速度造成的陀螺常值误差为1.20×10-4(°/h),虽然较小但是需要加以控制。从图中可以看出,随着加速度的增大,所有的误差项都增大,加速度的作用方向角ψ的变化使得误差呈周期性变化。控制方式I的控制精度最低,可以看出加速度导致的耦合误差较小可以忽略不计。以下主要讨论控制因数误差和陀螺常值误差。
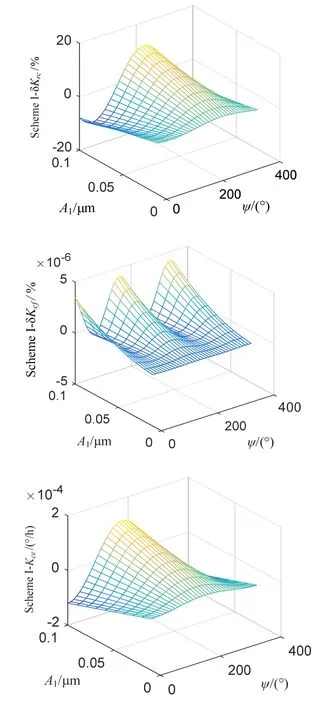
图8 控制方式I速率控制系统误差率Fig.8 Rate control system error rate of scheme I
从图9中可以看出,控制方式II可以使加速度导致的速率控制因数误差率降到 7.91%,陀螺常值误差下降到8.42×10-5(°/h)。可以看出,控制方式II从一定程度上减小了加速度对速率激励电极的影响,并不能将误差抑制到没有影响的程度,但是将陀螺的常值误差控制在了10-4(°/h)的范围内,以下不用讨论加速度导致的陀螺常值误差。
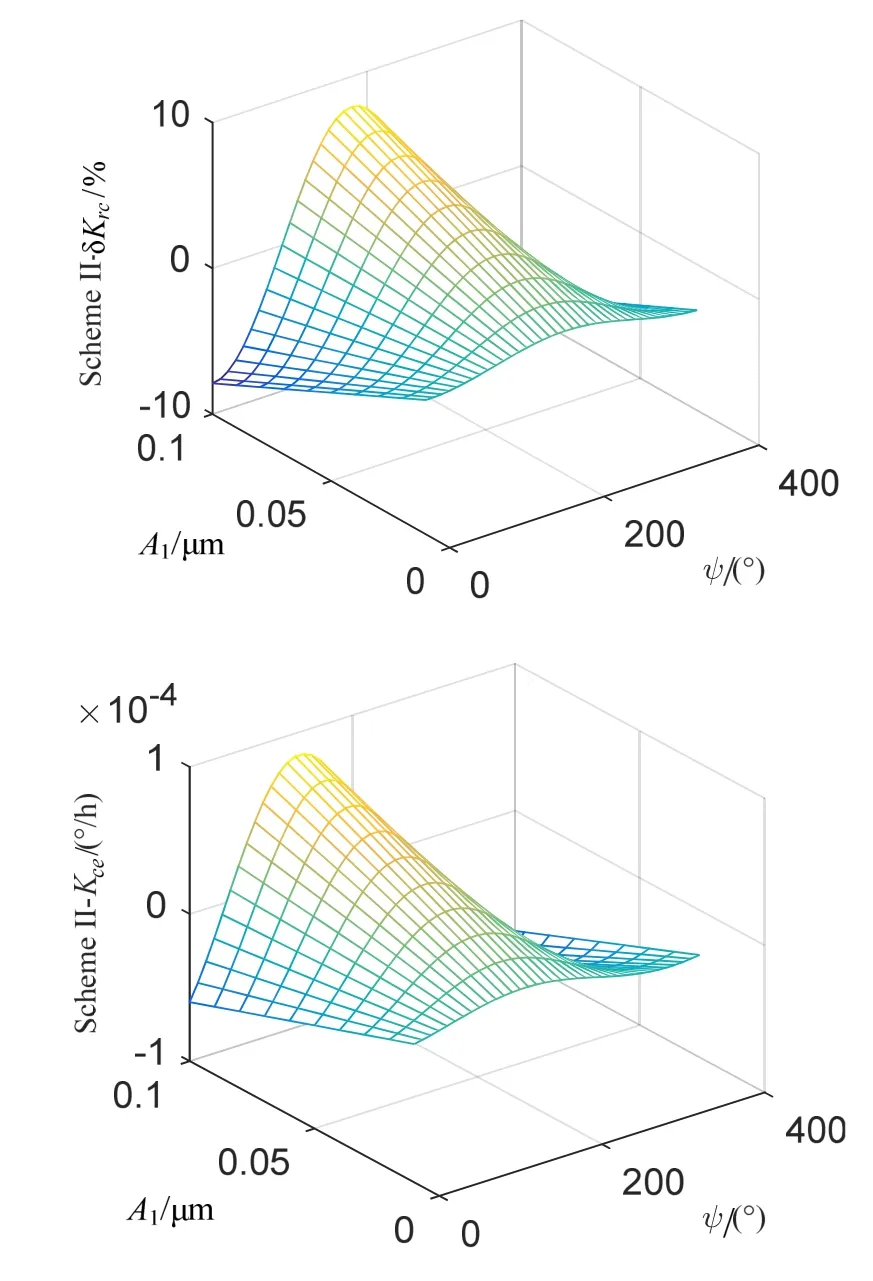
图9 控制方式II速率控制系统误差率Fig.9 Rate control system error rate of scheme II
从图10中可以看出,控制方式III使速率控制因数误差率最大值减小到 0.0164%,说明即使有加速度地影响,速率控制系统也能很好地控制陀螺的输出。控制方式 III利用电极相对分布的互补优势比控制方式II的差分控制取得更好的控制效果,能更好地抑制加速度对速率激励电极的影响。
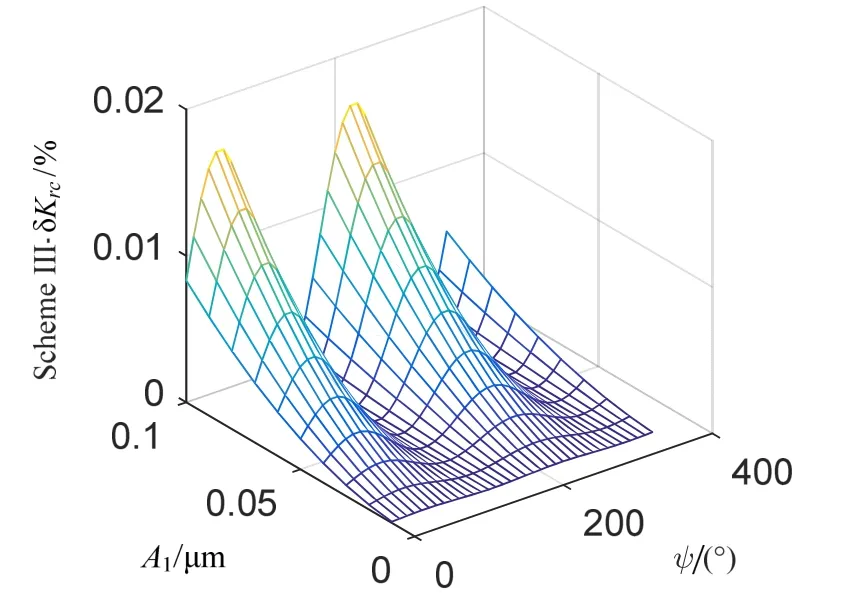
图10 控制方式III速率控制系统误差率Fig.10 Rate control system error rate of scheme III
4 结 论
本文详细研究了在多电极激励条件下的HRG谐振子动力学特性,分析了加速度对控制系统激励电极的影响。设计了三种反馈控制系统,分析了加速度导致的谐振子变形对三种反馈控制系统的影响,进而对陀螺输出的影响。最终得出以下结论:
1)利用激励电极作用下的谐振子动力学方程说明了控制方式III具有很好的反馈控制特性和鲁棒性,加速度对振幅激励电极影响很小。
2)加速度对控制方式I、II的速率激励电极影响较大,在分析加速度导致HRG漂移时必须考虑对速率控制因数及陀螺常值误差的影响。
3)通过合理配置激励电极的方式,控制方式III较大程度上削弱了加速度对振幅、速率控制系统激励电极的影响。相比于控制方式I、II,控制因数误差减小为原来的10-3倍。
参考文献(References):
[1] Матвеев В А, Липатников В И, Алехин А В. Проектирование. Волнового твердотелъного гироскопа[M].Издателъство МГТУ имени Н. Э. Баумана, 1998: 1-66.
[2]Rozelle D M. The hemispherical resonator gyro: from wineglass to the planets[C]//The 19th AAS/AIAA Space Flight Mechanics Meeting, 2009: 1157-1178.
[3]Wang X, Wu W Q, Luo B, et al. Force to rebalance control of HRG and suppression of its errors on the basis of FPGA[J]. Sensors, 2011, 11(12): 11761-11773.
[4]Song J W, Song H M, Lee Y J, et al. Design of oscillation control loop with coarse-precision mode transition for solid-state resonant gyroscope[J]. IEEE Sensors Journal,2016, 16(6): 1730-1742.
[5]Qi J Y, Ren S Q, Feng S W, et al. Random error analysis of hemispherical resonator gyro[J]. Journal of Chinese Inertial Technology, 2009, 17(1): 98-106.
[6]Wang X, Wu W Q, Fang Z, et al. Temperature drift compensation for hemispherical resonator gyro based on natural frequency[J]. Sensors, 2012, 12(5): 6434-6446.
[7]周小刚, 汪立新, 佘嫱, 等. 半球谐振陀螺温度补偿与实验研究[J]. 宇航学报, 2010, 31(4): 1083-1087.Zhou X G, Wang L X, She Q, et al. HRG temperature compensation and experiment research[J]. Journal of Astronautics, 2010, 31(4): 1083-1087.
[8]Xu Z Y, Yi G X, Qi Z Y, et al. Structural optimization research on hemispherical resonator gyro based on finite element analysis[C]//The 35th Chinese Control Conference,Chengdu, China, 2016: 5737-5742.
[9]Dai C L, Pi D C, Fang Z, et al. A novel long-term prediction model for hemispherical resonator gyroscope’s drift data[J]. IEEE Sensors Journal, 2014, 14(6): 1886-1897.
[10]伊国兴, 谢阳光, 王常虹, 等. 加速度对半球谐振陀螺振动检测系统影响分析[J]. 中国惯性技术学报, 2013,21(5): 676-681.Yi G X, Xie Y G, Wang C H, et al. Analysis of acceleration influence on HRG vibration detection system[J]. Journal of Chinese Inertial Technology, 2013, 21(5): 676-681.

