线性回归分析技术推估海底地形
范 雕,李姗姗,孟书宇,邢志斌,李新星
(1. 信息工程大学,郑州 450001;2. 西安航天天绘数据技术有限公司,西安 710054)
全球地形包括海底地形和陆地地形两个部分,作为全球地形的重要组成部分,海底地形在地球科学研究方面应用广泛。而电磁波在水中衰减的特性限制了遥感方法对深海的测量,从而,获得深海区域的水深数据主要依靠船载声呐系统,然而利用声呐技术对海域进行点、线和带状水深数据的采集,不仅耗时耗力,而且水深测量数据覆盖很不均匀,且主要集中在北半球。卫星测高能够在全球范围内全天候,重复、准确的提供海洋、冰面等表面高度的观测值,提高了观测、利用海洋的效率,使我们能够进行与之相应的系统研究,提炼出丰富的海洋信息[1-3]。
自1978年Seasat测高卫星发射成功以来,通过卫星测高技术建立海深模型也随之展开[4-12]。Kim et al.在椭圆形海山模型基础上,利用重力异常垂直梯度数据研究了全球的海山分布情况[13]。吴云孙等利用卫星测高得到的重力异常垂直梯度数据,采用FFT方法解算了中国南海海底地形,反演结果并不理想[14]。Wessel et al.利用Geosat和ERS-1测高卫星解算的重力异常垂直梯度研究了太平洋板块上的海山分布,提出重力异常垂直梯度具有放大短波信号、抑制长波信号的功能[15]。通常的海底地形反演技术需要知道诸多海底地球物理信息,由于海底地形复杂多样,相关参数的获取并不简单且解算过程复杂。Smith et al.[16]提出的线性回归分析技术反演海底地形巧妙地回避了这些问题,且计算简单。
目前,国内依据线性回归分析推估海底地形主要利用重力异常垂直梯度数据进行试验[17-18],如胡敏章等[19]采用重力异常垂直梯度反演了全球海底地形,欧阳明达等[20]利用测高重力异常、垂线偏差和大地水准面计算了重力异常垂直梯度,进而根据重力异常垂直梯度与海深的线性关系开展了中西太平洋海域的反演计算等。另外,根据线性回归分析反演海底地形关键在于比例因子的获取,目前国内外学者多采用将船测点上获得的比例因子进行格网化,进而获取海深模型格网点上的比例因子,从而构建海底地形模型。
基于以上分析,本文通过研究重力异常与海深的关系[21],开展了以重力异常和重力异常垂直梯度数据作为输入数据,采用线性回归分析技术反演海底地形的研究。同时,提出了一种利用格网点周围数据,采用线性拟合方法获取重力数据与海深线性关系中的比例系数和常数项,依据得到的比例系数和常数项推估海底地形的新方法。然后,以重力异常和重力异常垂直梯度为数据源,分别采用传统方法和本文方法计算比例因子,在西南太平洋相关海域开展了数值分析试验。利用实际测深数据作为外部检核条件,将海深计算结果与国际上通用的 ETOPO1海深模型和 DTU10海深模型进行了精度对比分析。
1 原理与方法
重力导纳函数表征将海底地形转换为重力异常的能力。如图1所示,依据导纳函数反演海底地形可表示为

其中:r为研究点向径;k为频率x、y方向的模,为重力异常的傅里叶变换;为傅里叶逆变换;Z(k)为导纳函数。

图1 质量亏损与重力异常关系Fig.1 Relationship between mass loss and gravity anomalies
我们知道,实际洋壳密度结构非常复杂,地震p波速度结构表明洋壳具有分层密度机制。将洋壳分为两层进行考虑,同时顾及海山密度和海山周围凹陷区域的沉积填充物密度(如图2所示)。

图2 洋壳分为两层的情况Fig.2 Oceanic crust which is divided into two layers
此时,顾及地壳挠曲的重力异常导纳函数为公式(2):

其中:G为地球引力常数,通常取 6.672×10–8cm3/(g·s2);γ为正常重力;D为岩石圈挠曲刚度,E为弹性模量(一般取 1011N/m2),Te为有效弹性厚度,v为泊松比(一般取0.25);h0为海平面到平均海深面的距离;wρ为海水密度;ρload海山密度;inρ为地壳凹陷区密度;分别为上地壳和下地壳密度;分别为上地壳和下地壳厚度;ρm为地幔密度。
经过试验分析发现,双层模型导纳函数与单层模型导纳函数差别很小,尤其在有效弹性厚度较大时,两者几乎完全一致[22]。因而在实际处理中常常将洋壳简化为单层,这样不仅能使数学模型简化,同时也能得到理想的效果。
根据文献[21]中公式(10),直接给出单层洋壳在不顾及地壳挠曲情况下重力异常导纳函数为:

其中,Δρ为地壳与海水的密度差异,其他符号意义同上。
由重力异常垂直梯度与重力异常之间的导数关系,依据傅里叶变换求导法则[23],对式(3)求导得到不顾及挠曲补偿情况下,重力异常垂直梯度的导纳函数为:

由于海底地形在一定波段内与重力异常和重力异常垂直梯度相关性高,因而进行反演实验时通常在特定波段内对海深进行反演,此时需要对重力异常和重力垂直梯度进行滤波处理,进而计算对应波段的海深。
不顾及地壳挠曲均衡环境下,重力异常经滤波处理计算特定波段的海深可表示为下式:
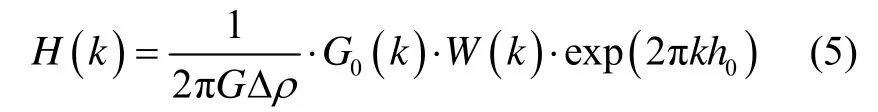
其中:H(k)和G0(k)分别为海深h和重力异常Δg在频率域上的表达式;W(k)为根据实验情况设计的带通滤波器。滤波器的使用可消除重力异常波段中板块挠曲的影响。
同理,不顾及地壳挠曲均衡环境下,重力异常垂直梯度经滤波处理计算特定波段的海深可表示为:

观察式(5)和式(6)可知,重力异常和重力异常垂直梯度经滤波并向下延拓后的结果与海底地形存在较好的线性关系。如对于重力异常而言,经滤波和向下延拓处理后的重力异常与残余海深呈近似线性关系,假设理论比例系数为S,则延拓后的重力异常与比例因子的乘积即为特定波段的海深值。加上其他波段的海深值,即为最终的海底地形模型。
但是,由于海底地质构造复杂,诸多地球物理参数难以精确确定,其线性关系一般不由式(5)和式(6)直接计算得到。实际计算中,常采用线性回归分析技术对特定波段内的重力异常与重力异常垂直梯度和海底地形进行线性S(x)拟合,进而获得试验区域内重力异常、重力异常垂直梯度和海底地形比例系数的计算值。其他波段海底地形d(x)与反演波段内的海底地形相加即得到全波段的海底地形

式中,y(x)表示经滤波和延拓等技术处理后的重力异常或者重力异常垂直梯度。计算流程如图3所示。
1)获取反演波段的重力异常/重力异常垂直梯度。根据海深和重力异常/重力异常垂直梯度的相干性特征,将格网化重力异常/重力异常垂直梯度经过带通滤波和向下延拓等技术处理,获得反演波段的重力异常/重力异常垂直梯度。

图3 传统的线性回归分析技术流程Fig.3 Traditional technical processes of linear regression analysis
2)获取长波段海深数据。船测海深点经格网化技术处理得到格网化海深模型,并依据和重力异常/重力异常垂直梯度的相干性分析结果,经过低通滤波处理获得长波段海深。
3)解算比例因子。将步骤 1获得的反演波段的重力异常/重力异常垂直梯度内插到船测点得到参考重力数据,将步骤2得到的长波段海深内插到船测点并与船测点海深做差获得船测点参考海深。船测点参考海深与船测点参考重力异常/重力异常垂直梯度之比即为比例因子。
4)构建海底地形模型。步骤 3获得的船测点上比例因子格网化获得格网化比例因子,格网化比例因子与格网化反演波段重力数据相乘得到反演波段海底地形,然后将各个波段海底地形相加获得最终的海底地形模型。
由以上步骤可以看出,线性回归方法构建海深模型的关键在于比例因子的解算。传统的比例因子解算是通过将船测点上的比例因子格网化,进而构建海底地形模型(图3所示流程)。这个过程只顾及了重力数据与海深线性关系中的一次项,结果可能有所偏差;同时比例因子的格网化过程难免存在误差,进而影响最终模型的构建。
为此,本文提出了一种解算比例因子的新方法。如图4反演波段内的海深和重力数据呈现明显的线性关系。因而本文在计算重力数据格网点比例因子时,利用计算点周围 20′范围内的重力数据和海深数据进行拟合,获得线性关系中的一次项和常数项。依据得到的比例系数和常数项推估反演波段海底地形,进而构建研究海域的海底地形模型。

图4 反演波段重力数据与海深线性拟合Fig.4 Linear fitting gravity data and bathymetry in inversion waveband
2 试验结果与分析
2.1 数据准备与前期处理

图5 研究区域数据Fig.5 Data of studied area
本文选取西南太平洋相关海域 6°×6°(156°E~162°E, 22°N~28°N)范围作为试验区域。数据来源如下:① 卫星测高重力异常数据来源于丹麦科技大学(Technical University of Denmark)空间实验室(DTU Space)发布的1′ 1′× DTU10模型(图5(a))。② 重力异常垂直梯度数据来自SIO,UCSD(Scripps Institution of Oceanography, University of California, San Diego),版本V24.1(图5(b)),该版本重力异常垂直梯度模型于2016年2月发布。相较于以前的V23版本,V24.1加入了超过1年的Cryosat-2卫星数据[24]。③船测海深数据来源于 NGDC(The National Geophysical Data Center)发布的研究海域实测数据。首先根据3σ准则对获取的测深数据进行粗差剔除,然后选择其中大约五分之四的船测点作为控制点(图 5(c)中黑色十字所示,一共20403个点),剩下的测深数据作为用于外部检核的检核点(图5(c)中红色三角形所示,一共5108个测深点),图5(c)中背景为ETOPO1海深模型。
高职教育的专业设置要谨慎选择。高职学校在专业设置方面不应该追求广而多,而应该追求精而深。要对自己的优势有全面的了解,并在对社会人才需求有充分了解的情况下,结合自己的优势设置相应学科。此外,社会发展日新月异,对人才的要求也会不断地发生变化,告知学校也要根据市场的变化及时调整自己的人才培养方式。
采用相干性(相关性的频率域表示)分析方法[25-26]对海深与重力异常/重力异常垂直梯度进行相干性分析,获得信号在频率域上的相干性[27]结果如图6所示。
图 6中黑色圆点和蓝色圆点分别表示重力异常和重力异常垂直梯度与海深在频率域上的相干性结果。相干性结果表明,波长在大于20 km的部分,重力异常和重力异常垂直梯度与海深均表现出了较强的相关性(图6中红色实线以上部分表示相干性大于0.5的波段)。综合考虑国内外研究经验,本文最终选择20~200 km波段重力信息为海底地形反演波段。另外,本文涉及滤波及延拓[28]等过程,需将重力和海深数据转换到频率域进行处理,为消除边缘效应的影响,试验过程中选取的研究范围在纵向和横向分别向外延拓1°,最后对反演结果进行截取处理得到研究海域的海底地形。

图6 重力数据与海深的相干性Fig.6 Coherency between gravity data and bathymetry
2.2 构建海底地形模型
按照构建海底地形模型步骤,分别将重力异常和重力异常垂直梯度进行带通滤波处理,获得20~200 km波段的重力数据和海深数据,如图7所示。从图7(a)、图7(b)和图7(c)比较可以看出,重力异常和重力异常垂直梯度与海深表现出良好的相关性。

图7 反演波段海深和重力数据Fig.7 Bathymetry and gravity data in inversion waveband
依据传统确定比例因子步骤,采用三次样条插值方法,分别将反演波段重力数据和海深数据内插到船测点,而后利用三次多项式格网化技术将船测点上获得的比例因子格网化,分别以重力异常和重力异常垂直梯度为数据源,获取的比例因子如图8(a)和图8(b)所示。对比图5(c)和图8可以看出:研究海域的西侧部分地势平坦起伏较小,比例系数较小,试验海域东侧部分存在较多海山等起伏较大的地貌形态,比例系数相对较大,反映了重力数据与海深较强的相关性。
采用本文提出的方法:利用格网点周围20′范围内的重力和海深数据,使用抗差线性回归技术解算海深和重力数据的比例因子和常数项。其中,海深和重力异常解算的比例因子和常数项如图9所示,图10为依据相同方法获得的研究海域海深与重力异常垂直梯度比例因子和常数项。

图8 比例因子格网Fig.8 Grid of scale factor
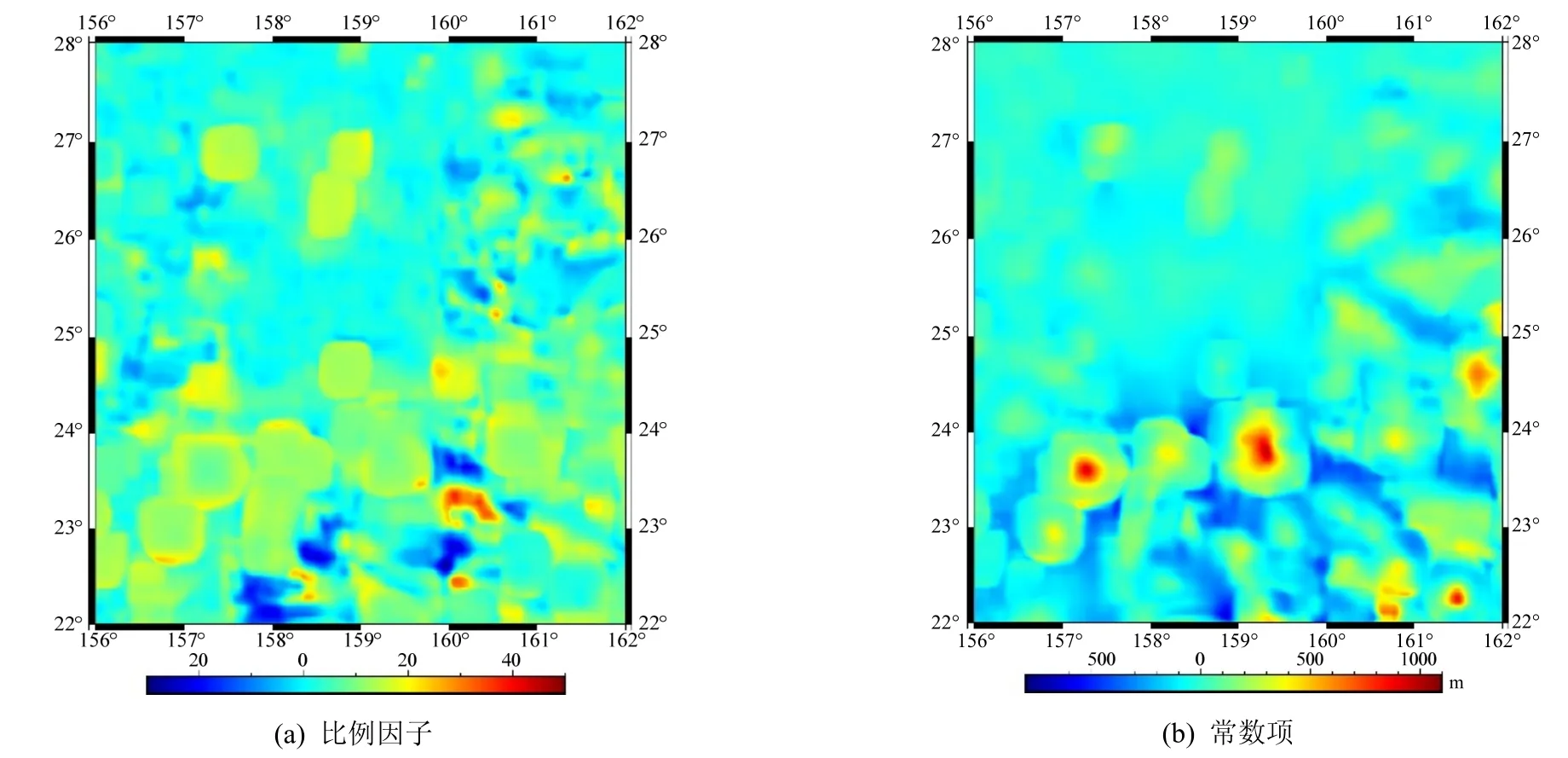
图9 海深和重力异常线性回归分析结果Fig.9 Linear regression analysis results of bathymetry and gravity anomalies

图10 海深和重力异常垂直梯度线性回归分析结果Fig.10 Linear regression analysis results of bathymetry and vertical gravity gradient anomalies
从图 9(a)和图 10(a)可以更加明显地看出比例因子与海底地貌的关系,说明了本文提出的方法与传统方法确定的比例因子具有空间分布的一致性,而且依据本文方法获得的比例因子与海底地貌形态的内在联系更加明显。同时,回归分析获得的海深与重力数据的常数项与海底地形也具有类似的特点,从而验证了本文提出的解算海深和重力数据比例因子与常数项方法的可行性。
分别以重力异常和重力异常垂直梯度为数据源,按照传统线性回归分析方法与本文提出的新方法构建海底地形模型。为了描述方便,按照传统线性回归分析方法,以重力异常和重力异常垂直梯度获得的海底地形模型分别记为模型1和模型2,按照本文提出的方法,以重力异常和重力异常垂直梯度获得的海底地形模型分别记为模型 3和模型4,构建的海底地形模型如图11所示。
图11中实心红点表示构建的海深模型内插到外部检核点得到的检核点处海深插值与检核点处海深差值大于 300 m的检核点空间分布情况。其中模型1、模型2、模型3和模型4中差值大于 300 m的检核点分别有231个、235个、189个和197个,分别占检核点总数的4.5%、4.6%、3.7%和 3.8%左右。利用本文方法构建的海底地形模型较大差值点个数相较于传统方法,较大差值的个数减少了近1%。图 11(a)和图 11(b)对比发现,研究海域西侧部分,海底地形较为平坦的海域,利用重力异常垂直梯度反演的海深结果差值点(差值300 m以上)个数明显少于采用重力异常构建的海深模型1。分析比较利用相同重力数据获得的模型1和模型3(重力异常为数据源)以及模型2和模型4(重力异常垂直梯度为数据源)可以清晰看出,在海底地形平坦的西侧海域或者地形起伏较大的南侧和东侧部分海域,模型3和模型4较大差值点个数均明显少于模型1和模型2。研究海山附近的差值点分布情况可以看出,本文方法和传统方法在反演海底地形方面各有不同的优势,如在(157.2°E, 23.6°N)和(159.4°E, 23.8°N)位置的两座海山附近,模型3和模型4较大差值点主要集中在海山上,在靠近海山区域精度较好,而模型1和模型2在靠近这两座海山的海域,较大差值点较为密集,海山上的较大差值点反而较少。

图11 海底地形模型Fig.11 Seabed terrain model
2.3 精度评价
进一步分析比较构建的四种海底地形模型,利用外部检核条件,同时引入目前常用的ETOPO1海深模型和DTU10海深模型,将海深模型值采用三次样条插值方法内插到检核点并与检核点处海深值做差,分别统计各个海深模型的较差结果并进行精度评价,各模型的检核统计结果见表1。
从表1检核统计结果可以看出,模型1和模型2与检核点差值最大值分别为5427.00 m和4199.70 m,最小值分别为–2388.70 m和–2609.20 m,其海最值结果明显大于ETOPO1模型和DTU10模型,更大于模型3和模型4最值统计结果。同时,模型3和模型4的最小值分别为-572.77 m和–522.11 m,明显优于其他四种海深模型。对比以上6种模型与检核点的差值均方差发现,检核精度由高到低依次为模型4、模型3、ETOPO1模型、模型2、模型1和DTU10模型,均方差分别为118.77m、122.57m、150.18m、160.07m、173.81m和253.57m,同时模型的检核精度也从插值点与检核点的相关系数大小得到验证。从构建海深模型的数据源可以看出,利用重力异常反演的海深模型1和模型3均方差大于利用重力异常垂直梯度推估的海深模型2和模型4,其中模型2相较模型1精度提高了约8%,模型4相比于模型3精度提高了3%左右。模型1和模型2精度略低于ETOPO1模型,优于DTU10模型,与DTU10海深模型相比,精度提高近58%。模型3和模型4精度最高,其中利用重力异常垂直梯度数据,采用本文方法构建的海深模型4精度最高,与模型2相比较,精度提高了35%左右,模型插值和检核点海深相关系数为0.9923;模型4的精度也明显优于ETOPO1模型,相比于 DTU10模型,检核点差值精度更提高了一倍有余。反映了本文利用格网点周围数据,采用线性拟合方法获取重力数据与海深线性关系中的比例系数和常数项,进而构建海深模型相比传统方法构建的海深模型和常用的海深模型具有较大的优越性。

表1 模型检核统计结果Tab.1 Statistical results of the models m
进一步验证利用本文方法构建的海深模型精度,定义模型内插到检核点并与检核点海深的差值与检核点海深之比为相对误差,各模型相对误差统计结果如表2所示。表2中相对误差统计结果显示;模型4的相对误差平均值最小,仅为0.06%;DTU10海深模型相对误差平均值最大为–1.28,明显高于其他5种海深模型。同时,DTU10模型标准差也远远大于其他5种海深模型的相对误差标准差统计结果,另外5种海深模型相对误差统计结果相差不大,其中模型2好于模型1,模型4优于模型3,说明重力异常垂直梯度反演海深优于利用重力异常反演的海深结果。

表2 各模型相对误差统计结果Tab.2 Statistical results of each model’s relative error
3 结 论
本文选取西南太平洋相关海域6°×6°(156°E~162°E, 22°N~28°N)范围作为试验区域。利用重力异常和重力异常垂直梯度数据,采用线性拟合方法获取重力数据与海深线性关系中的比例系数和常数项,并依据得到的比例系数和常数项分别构建了以重力异常为数据源和重力异常垂直梯度为数据源的海底地形模型。同时以实际测深点作为外部检核条件,将按照本文方法构建的海深模型与依据传统内插和格网化方法获取比例因子构建的海底地形模型,以及国际上常用的ETOPO1海深模型和DTU10海深模型进行了精度分析比较,可以得到以下有益结论:
1)通过不同方法获取的比例因子与海底地貌呈现一定的内在联系,地形平坦海域,得到的比例因子较小,分布较多海山的地形起伏较大海域,比例因子相对较大,反映了重力数据与海深较强的相关性。
2)以重力异常/重力异常垂直梯度为数据源,采用本文提出的依据线性拟合方法获取比例系数和常数项方法构建的海底地形模型3和模型4,检核点差值大于300 m的船测点数量相较于传统方法构建的海底地形模型1和模型2,较大差值点减少了近1%。
3)构建海底地形模型中,不同方法对于不同的海底地形具有各自不同的优势。分析检核差值结果发现:模型3和模型4总体上(地形平坦海域或者地形起伏较大海域)反演效果优于模型1和模型2,在靠近海山区域,模型3和模型4反演结果优于模型1和模型2;在海山部分,模型1和模型2反演精度又好于模型3和模型4。
4)比较不同数据源反演海底地形的结果表明,以重力异常垂直梯度构建的海底地形模型的检核精度优于以重力异常为输入数据构建的海底地形模型。同时,采用本文方法构建的海底地形模型检核精度最高,相较于传统方法获取的海底地形模型,精度最高提升了46%左右,与ETOPO1海深模型和DTU10海深模型相比较,模型精度最大提高了一倍有余。
反演海底地形的研究中,在海山、海沟、洋中脊等海底地貌形态复杂和地形起伏剧烈的海域,反演效果往往不佳,而本文试验发现不同的反演方法对于不同的海底地貌具有不同的反演精度,对于不同海底地形的反演结果呈现互补效应。从而,联合不同数据,融合不同反演方法构建海底地形模型可能是解决这类问题的一个途径,这也是笔者目前正在研究的问题。
参考文献(References):
[1]Leuliette E W, Nerem R S, Mitchum G T. Calibration of topex/poseidon and jason altimeter data to construct a continuous record of mean sea level change[J]. Marine Geodesy, 2004, 27(1-2): 79-94.
[2]Niedzielski T, Kosek W. Minimum time span of topex/poseidon, jason-1 and jason-2 global altimeter data to detect a significant trend and acceleration in sea level change[J]. Advances in Space Research, 2011, 47(7): 1248-1255.
[3]李建成, 金涛勇. 卫星测高技术及应用若干进展[J].测绘地理信息, 2013, 38(04): 1-8.Li J C, Jin T Y. On the main progress of satellite altimetry and its applications[J]. Journal of Geomatics, 2013, 38(4): 1-8.
[4]Hwang C. A bathymetric model for the South China Sea from satellite altimetry and depth data[J]. Marine Geodesy,1999, 22(1): 37-51.
[5]Wang Y M. Predicting bathymetry from the Earth’s gravity gradient anomalies[J]. Marine Geodesy, 2000,23(4): 251-258.
[6]Ramillien G, Cazenave A. Global bathymetry derived from altimeter data of the ers-1 geodetic mission[J].Journal of Geodynamics, 1997, 23(2): 129-149.
[7]Arabelos D. On the possibility to estimate ocean bottom topography from marine gravity and satellite altimeter data: an experiment in the central mediterranean[J]. Earth& the Universe, 1997.
[8]Arabelos D. On the possibility to estimate ocean bottom topography from marine gravity and satellite altimeter data using collocation[J]. Journal of Geophysical Research,1997, 95: 105-112.
[9]罗佳, 李建成, 姜卫平. 利用卫星资料研究中国南海海底地形[J]. 武汉大学学报(信息科学版), 2002, 27(3):256-260.Luo J, Li J C, Jiang W P. Bathymetry prediction of South China Sea from satellite data[J]. Geomatics and Information Science of Wuhan University, 2002, 27(3): 256- 260.
[10]Dixon T H, Naraghi M, Mcnutt M K, et al. Bathymetric prediction from SEASAT altimeter data[J]. 1983, 88:1563-1571.
[11]Mohanty K K, Majumdar T J, Kunte P D, et al. Mapping of sea bottom topography over western offshore, India using TOPEX/ERS-1 altimeter data1[J]. Acta Astronautica, 1997, 41(3): 151-154.
[12]Rapp R H. The Determination of geoid undulations and gravity anomalies from seasat altimeter data[J]. Journal of Geophysical Research Oceans, 1983, 88(C3): 1552-1562.
[13]Kim S S, Wessel P. New global seamount census from altimetry-derived gravity data[J]. Geophysical Journal International, 2011, 186(2): 615-631.
[14]吴云孙, 晁定波, 李建成, 等. 利用测高重力梯度异常反演中国南海海底地形[J]. 武汉大学学报(信息科学版), 2009, 34(12): 1423-1425.Wu Y S, Chao D B, Li J C, et al. Recovery of ocean depth model of South China Sea from altimetric gravity anonalies[J]. Geomatics and Information Science of Wuhan University, 2009, 34(12): 1423-1425.
[15]Wessel P, Lyons S. Distribution of large Pacific seamounts from GEOSAT/ERS-1: implications for the history of intraplate volcanism[J]. Journal of Geophysical Research Solid Earth, 1997, 102(B10): 22459-22475.
[16]Smith W H F, Sandwell D T. Bathymetric prediction from dense satellite altimetry and sparse shipboard bathymetry[J]. Journal of Geophysical Research Solid Earth, 1994,99(B11): 21803-21824.
[17]胡敏章, 李建成, 邢乐林, 等. 海底地形反演方法比较[J]. 大地测量与地球动力学, 2014, 34(05): 11-16.Hu M Z, Li J C, Xing L L, et al. Comparative analysis of methods for bathymetry prediction[J]. Journal of Geodesy And Geodynamics, 2014, 34(05): 11-16.
[18]李倩倩, 鲍李峰. 测高重力场反演海底地形方法比较[J]. 海洋测绘, 2016, 36(5): 1-4.Li Q Q, Bao L F. Comparative analysis of methods for bathymetry prediction from altimeter-derived gravity anomalies[J]. Hydrographic Surveying and Charting,2016, 36(5): 1-4.
[19]胡敏章,李建成,邢乐林. 由垂直重力梯度异常反演全球海底地形模型[J]. 测绘学报, 2014, 43(6): 558-565.Hu M Z, Li J C, Xing L L. Global bathymetry model predicted from vertical gravity gradient anomalies[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 558-565.
[20]欧阳明达, 孙中苗, 翟振和, 等. 海洋垂直重力梯度异常的计算及其在地形反演中的应用[J]. 大地测量与地球动力学, 2016, 36(9): 766-769.Ouyang M D, Sun Z M, Zhai Z H, et al. The calculation of vertical gravity gradient anomalies and its application in bathymetry inversion[J]. Journal of Geodesy and Geodynamics, 2016, 36(9): 766-769.
[21]Kim K B, Hsiao Y S, Kim J W, et al. Bathymetry enhancement by altimetry-derived gravity anomalies in the East Sea (Sea of Japan)[J]. Marine Geophysical Researches,2010, 31(4): 285-298.
[22]胡敏章. 海底地形反演与地壳均衡研究[D]. 武汉: 武汉大学, 2013.Hu M Z. Research on bathymetry prediction and crust isostasy[D]. Wuhan: Wuhan University, 2013.
[23]Parker R L. The rapid calculation of potential anomalies[J].Geophysical Journal International, 1973, 31(4): 447-455.
[24]Sandwell D, Garcia E, Soofi K, et al. Toward 1-mgal accuracy in global marine gravity from cryosat-2, envisat,and jason-1[J]. Leading Edge, 2013, 32(8): 892-899.
[25]Lewis B T R, Dorman L R M. Experimental isostasy: 2.an isostatic model for the U.S.A. derived from gravity and topographic data[J]. Journal of Geophysical Research,1970, 75(17): 3367-3386.
[26]Foster M R. The coefficient of coherence: its estimation and use in geophysical data processing[J]. Geophysics,1967, 32(4): 602.
[27]Luis J F, Neves M C. The isostatic compensation of the azores plateau: a 3D admittance and coherence analysis[J]. Journal of Volcanology and Geothermal Research,2006, 156(1): 10-22.
[28]徐世浙. 迭代法与FFT法位场向下延拓效果的比较[J].地球物理学报, 2007, 50(1): 285-289.Xu S Z. A comparison of effects between the iteration method and FFT for downward continuation of potential fields[J]. Chinese Journal of Geophysics, 2007, 50(1):285-289.
——以大班艺术领域为例

