基于自适应分类容错滤波的SINS/GNSS组合导航方法

郭慧娟，刘慧英，石 静，孙景峰

（西北工业大学 自动化学院，西安 710072）

捷联惯性导航系统（Strapdown Inertial Navigation System, SINS）作为一种自主式导航系统得到了广泛应用，通常将其与全球定位系统（Global Navigation Satellite System, GNSS）组合使用，通过滤波算法进行数据融合，来保证惯性导航系统的长期精度[1-3]。而在实际应用中系统的数学模型往往是非线性的，所以EKF算法被广泛应用于SINS/GNSS组合导航系统中估计、补偿导航误差。虽然将GNSS与SINS组合使用并通过 EKF对两者输出的信息进行滤波可以克服惯性器件误差不断累积的缺陷，提高系统精度，但实际情况下GNSS量测信号极易受到周围环境、多路径效应等多种因素的影响，如环境中的无线电和强磁场会使GNSS测量值产生较大的速度误差和至少百米级位置误差，因此对滤波产生不利影响，严重时将导致状态的估计值明显偏离真实值，从而导致系统导航定位的准确性、可靠性变差[4]。所以，当GNSS量测输出中存在异常量测信号等故障时，如果仍采用EKF算法将SINS和GNSS输出的数据相融合，会导致精度降低甚至发散。为了解决GNSS信号异常这类软故障，很多学者对自适应滤波和鲁棒滤波进行研究。文献[4]利用系统的量测残差序列构造基于自适应多重渐消因子的鲁棒EKF算法（REKF）来解决系统中出现的任何类型故障；文献[5]利用量测残差提出了估计量测噪声的自适应滤波算法（AEKF），通过仿真证明了该算法在GNSS信号存在较大的位置误差时的有效性；文献[6-7]利用系统的残差序列或新息序列的协方差矩阵构造自适应滤波器来修正量测噪声方差阵和解决系统噪声不确定的问题，得到了较好的滤波效果。文献[4-5]中的REKF和AEKF在存在较大速度、位置误差时的滤波结果仍有明显发散，若故障时间较长就无法保障导航的精度；文献[5-6]利用单一的加权因子，无法对GNSS量测输出各通道的故障进行精确的加权。

本文针对SINS/GNSS组合导航系统中存在GNSS信号异常这类问题，提出一种基于EKF的自适应分类容错滤波算法。首先，通过比较系统残差协方差矩阵的实际值与理论值来检测 GNSS信号中是否存在异常，并区分异常的类型，然后针对不同程度的异常信号计算来进行修正，并且在滤波过程中加入UD分解来改善滤波的稳定性能。

1 SINS/GNSS组合系统非线性数学模型

考虑SINS/GNSS组合导航系统非线性数学模型[8]，

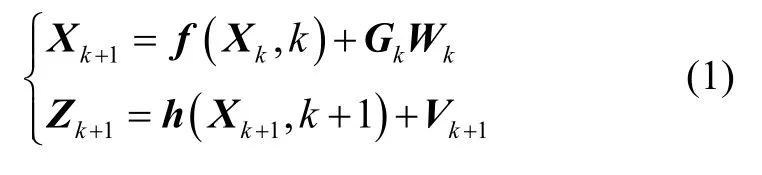
式中：δk,j为克罗内克（Kronecker）符号；Qk、Rk分别为系统噪声方差阵和量测噪声方差阵。

系统量测残差向量为

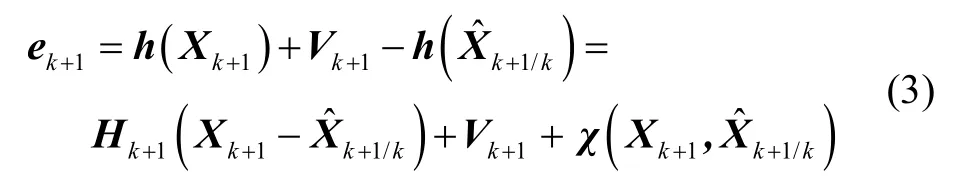
式中，Pk+1/k为一步预测均方误差阵，在EKF滤波方程中满足：

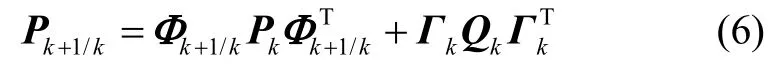
其中，Pk为估计均方误差阵：

且Kk满足：

2 自适应分类容错滤波设计

2.1 问题提出

在SINS/GNSS中，如果GNSS信号出现异常则会导致系统量测存在较大的误差，所以实际系统的量测噪声方差Rk+1并不能用固定值表示，否则会使EKF对量测值Zk+1和一步估计值利用的比例程度失衡，从而导致滤波发散。因此，为了方便实验观察，本文将量测噪声分为两部分：一部分为有固定方差系统量测噪声一部分为时变量测噪声且设两部分噪声互不相关，所以式(1)中的系统量测方程和式(5)可分别等价于

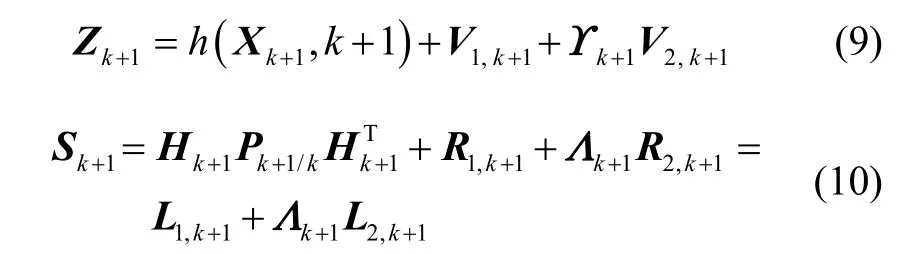
式中，Υk+1和Λk+1同为m×m维对角矩阵，分别为时变量测噪声和其方差的加权修正矩阵，非负定。设

同时，式(10)中：

基于上述分析与计算，本文提出的自适应分类容错滤波方法的滤波方程如式(15)～ (22)所示：

式中：Λk+1为加权因子矩阵，如式(11)所示。

在上述计算过程中，如果估计均方误差阵Pk为病矩阵或轻度负定会使Pk+1/k失去非负定性，再求取时Sk+1的求逆运算将会不存在或产生巨大的误差，从而导致的估计误差较大。针对上述问题，Thornton等[9]提出一种基于UD分解的滤波方法。本文也将UD分解应用到自适应分类容错滤波方法中，将Pk和Pk+1/k分别分解为TUDU 的形式：

2.2 加权矩阵Λk+1的确定

根据1.1节的分析，为降低GNSS信号异常对组合导航系统滤波精度和稳定性的不利影响，适当地选取Λk+1的值是设计自适应分类容错滤波算法的关键。

所以为了提高滤波精度，本文提出的自适应分类容错滤波算法在进行自适应分类加权矩阵的设计时，首先利用异常信号检测公式来求取η。根据η的归属范围，将GNSS出现的异常信号分为两类（A类异常和B类异常），并根据异常信号的分类来定义量测噪声方差加权阵Λk+1的求取方法。η的判定公式为：

式中，1η和ξ的值可根据系统的实际情况选取，在大量试验的基础上，对常规SINS/GNSS组合导航系统1η取值在100～500之间，ξ的取值不大于0.1。

根据上述分析，GNSS信号被分为三种情况：

（a）当由η的值判断 GNSS信号无异常时，

（b）当判断GNSS有A类异常信号时，由式(10)可知，Λk+1满足下列不等式：

所以，Λk+1取值的必要条件为α满足：

若α＜0，则α=0。当时，由式(27)推出Λk+1取值的充分条件为iα满足：

由上述推导可知，iα必须同时满足式(28)和式(29)，即所以，为了精确的加权修正异常信号，针对本文算法中Λk+1取值的充要条件为其每一个元素满足：

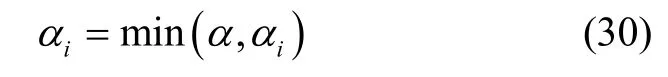
（c）当GNSS有B类异常信号输出时，利用残差序列协方差的无偏估计来求取Λk+1的值，残差序列协方差无偏估计表示为

式中，N为滑动窗口长度。式(10)和式(31)都包含了残差信息，所以本文提出的自适应容错滤波算法中的最小值可以由F范数来确定。设

式中：Λk+1为非负定矩阵，表示F范数。当J(Λ)取得最小值时，残差序列协方差无偏估计M就越接近残差序列协方差矩阵Sk+1(式(10))的值。所以，如何求出当J(Λ)取最小值时Λk+1的值是下文中首先要解决的问题。将式(32)展开如下：

且J（Λ）取得最小值的必要条件为

所以，对式(34)求偏导得：

由式(35)和式(36)得：

若α＜0，则α=0。当时，式(33)等价于

取得最小值。所以，αi的取值为

若αi＜0，则αi=0。为了精确的加权修正异常信号，由式(37)和式(40)可知，针对本文算法中Λk+1取值的充要条件为其每一个元素满足：

所以，上述为GNSS信号出现不同情况时，加权矩阵Λk+1的取值方法。原理为当GNSS信号出现A类异常时，Λk+1的取值越大，滤波增益矩阵Kk+1的值就会越小，在确定时对Ζk+1的利用权重减小；当GNSS信号出现B类异常时，本文通过F范数的方法求取Λk+1，从而使其将估计的故障噪声修正到正常范围，但若此时残差序列协方差无偏估计样本的选取仍包含当前值，则式(31)中M的取值仍会包含较大的量测误差，致使Λk+1的取值达不到修正系统量测噪声的目的，所以本文将M修正为由残差序列的历史值组成的样本来推导，即将式(31)修正为

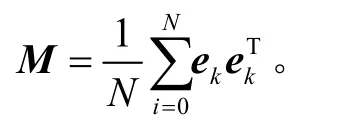
3 自适应分类容错算法在SINS/GNSS中的应用

3.1 SINS/GNSS系统滤波模型

针对SINS/GNSS组合导航系统，选取一组15维的系统状态变量：

式中：δΦE、δΦN、δΦU为姿态角误差；δVE、δVN、δVU、δL、δλ、δh分别为东北天方向的速度误差和经纬高度误差；ε为陀螺常值零漂；∇为加速度常值零偏。

系统误差模型[10]：

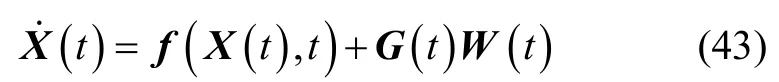
系统量测模型：

3.2 仿真实验及分析

实验平台为模拟的SINS/GNSS组合导航系统。进行仿真的SINS输出频率为200 Hz，其陀螺仪和加速度计的数据为：陀螺仪常值零漂和随机漂移分别为0.1(°)/h 和0.002(°)/h1/2，加速度计常值零偏和随机零偏分别为和。GNSS导航系统的输出周期为1 s，GNSS接收机东、北、天方向的速度误差均方根为0.5 m/s，位置误差均方根为10 m。假设飞机初始速度和初始航向角分别为0 m/s和0°，初始纬度、经度、高度分别为L0=34.27°、0λ=108.95°、h0=380 m，飞行过程中包括滑跑、爬升、转弯、匀速平飞等阶段，其飞行轨迹如图1所示。

为了对文中提到的算法进行更直观的比较，在已获得GNSS信号中，根据不同情况加入GNSS信号出现异常时的速度误差均方根值和位置误差均方根值，如表1所示。仿真时间为1000 s，且针对上述SINS/GNSS组合导航系统进行仿真时，取1η=334.2，ξ=0.1。

用上述数据对本文提出的自适应分类容错滤波算法（ACEKF）进行验证。为了进行比较，本文使用同一组数据对文献[4]提出的REKF和文献[5]提出的AEKF进行仿真，所得仿真实验结果如图2和图3所示。

由表1可知，本文在仿真的6个不同时间段内在GNSS正常信号的基础上分别加入不同程度的位置、速度误差，且根据本文异常信号检测分类算法，在时间段1和时间段4加入误差的GNSS信号，大部分时REKF算法出现了一定程度的发散状态，在时间段5，间内归属于A类异常，而在时间段2、3、5、6加入误差的GNSS信号则大部分时间内属于B类异常。图2和图3结果表明：本文提出的ACEKF与REKF、AEKF相比导航精度较高，且ACEKF与AEKF都优于文献[4]的REKF算法，其中在时间段1、2、4、5，REKF算法出现了一定程度的发散状态，在时间段5，AEKF的经、纬度误差与东、北向速度误差呈现了一定程度的发散状态，在其它时间段REKF和AEKF都能将速度误差和位置分别维持在0.5 m/s和10 m以内，而本文提出的ACEKF算法则可以一直维持上述精度。所以整体上，ACEKF相比上述两种算法误差小，在滤波过程中能够一直保持较高的精度，也更稳定。

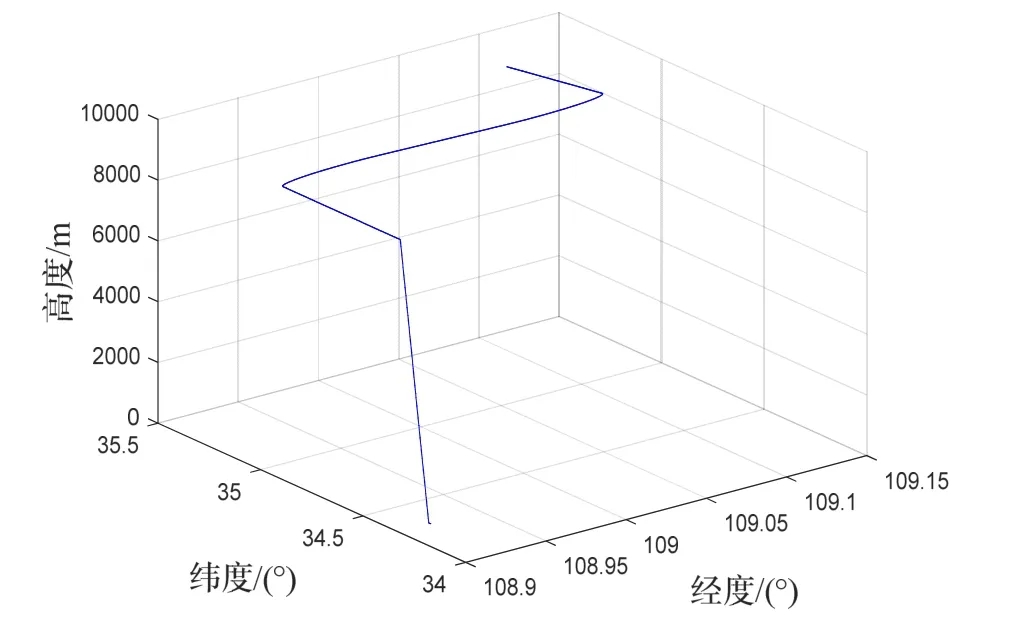
图1 飞机飞行轨迹Fig.1 Flight trajectory

表1 加入的GNSS信号的速度、位置误差均方根值Tab.1 Additional velocity and position errors of GNSS

图2 SINS/GNSS在GNSS信号异常时的位置误差Fig.2 Position errors of SINS/GNSS when there is abnormal GNSS signal

图3 SINS/GNSS在GNSS信号异常时的速度误差Fig.3 Velocity errors of SINS/GNSS when there is abnormal GNSS signal

表2和表3的数据比较了三种算法和EKF算法的位置和速度的平均绝对误差与均方根误差，可以看出采用本文提出的ACEKF方法具有较高的导航精度与稳定性：在GNSS信号存在异常情况下，其导航精度相比对基于实时估计量测噪声方差的 EKF至少提高95.6%，相比REKF和AEKF分别至少提高44.5%和24.6%。结果证明本文提出的ACEKF算法对GNSS异常信号有更强的容错能力。

表2 速度、位置平均绝对误差Tab.2 Mean absolute errors of velocity and position

表3 速度、位置误差均方根误差Tab. 3 RMSEs of velocity and position

4 结 论

本文针对 SINS/GNSS组合导航系统容易出现GNSS信号异常进而影响导航精度及系统稳定性等问题，提出一种基于EKF的自适应分类容错滤波方法，并在滤波过程中加入UD分解，最后将其应用到组合导航系统中。本文方法主要对GNSS异常信号进行检测分类，对不同类别的异常信号采用不同方法计算量测噪声的加权修正矩阵，以减弱异常数据对系统导航精度的影响。仿真结果表明：本文提出的ACEKF算法能准确地检测出GNSS异常信号，在GNSS信号出现异常情况下，其导航精度相比基于实时估计量测噪声方差的 EKF算法至少提高 95.6%，相比REKF和AEKF分别至少提高44.5%和24.6%，对异常量测值有较好的修正能力，且ACEKF算法的容错能力强，用其优化后的系统能够一直保持正常稳定的状态。

参考文献（References）：

[1]Zhao L, Qiu H Y, Feng Y M. Study of robust filtering application in loosely coupled INS/GNSS system[J].Mathematical Problems in Engineering, 2014: 1-10.

[2]Lim C H, Lim T S, Koo V C. New GNSS-aided SINU system modeling using an autoregressive model[J]. International Journal of Advance Robotic Systems, 2015, 12:1-13.

[3]Zhang B, Chu H, Sun T. Error prediction for SINS/GNSS after GNSS outage based on hybrid KF-UKF[J]. Mathematical Problems in Engineering, 2015: 1-10.

[4]Soken H E, Hajiyev C. REKF and RUKF for pico satellite attitude estimation in the presence of measurement faults[J]. Journal of Systems Engineering and Electronics, 2014, 25(2): 288-297.

[5]Yu M J. INS/GNSS integration system using adaptive filter for estimating measurement noise variance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012,48(2): 1786-1792.

[6]朱占龙, 单友东. 基于新息正交性自适应滤波的惯性/地磁组合导航方法[J]. 中国惯性技术学报, 2015, 23(1):66-70.Zhu Z L, Shan Y D. INS/GNSS integrated method based on innovation orthogonality adaptive Kalman filter[J].Journal of Chinese Inertial Technology, 2015, 23(1): 66-70.

[7]董宁, 徐玉娇, 刘向东. 一种带自适应因子的IMM-UKF 的 GNSS/BD-2 导航方法[J]. 宇航学报,2015, 36(6): 676-683.Dong N, Xu Y J, Liu X D. An IMM-UKF with adaptive factor for GNSS/BD-2 satellite navigation system[J].Journal of Astronautics, 2015, 36(6): 676-683. ()

[8]秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安：西北工业大学出版社, 2015: 198-205.Qin Y Y, Zhnag H Y, Wang S H. Kalman filtering and integrated navigation theory[M]. Xi’an: Northwestern Polytechnical University Press, 2015: 198-205.

[9]Thornton C L, Bierman G J. UDUT covariance factorization for Kalman filtering[J]. Control and dynamic systems, 1980: 65(4): 177-248.

[10]Ali J, Mirza M. Performance comparison among some nonlinear filters for a low cost SINS/GNSS integrated solution[J]. Nonlinear Dynamics, 2010, 61(3): 491-502.