“三角形”的解题方法

三角形是一种常见的图形,也是最基本的多边形,主要是认识三角形的特性,知道三角形任意两边的和大于第三边,会根据三角形角的特点给三角形分类,发现和掌握三角形的内角和是180°。
一、三角形的特性及解题方法
两点间所有的连线中线段最短。三角形三条边确定了,它的形状也就唯一确定了,并且三角形任意两边之和大于第三边。
例1.一个三角形两条边的长分别为2厘米和5厘米,那么,这个三角形第三条边的长是多少厘米?
[分析与解]根据三角形的特性,三角形任意两边之和大于第三边,可知两条较短边的长度之和一定大于第三边。如果第三条边是其中的较短边,那么2厘米加上第三条边的长度一定大于5厘米。因此,这个三角形第三条边的长应大于5-2=3(厘米)。如果第三条边是其中的最长边,那么第三条边的长度一定小于2+5=7(厘米)。由此可得,这个三角形的第三条边的长度大于3厘米且小于7厘米。
例2.画出下面三角形指定边上的高。
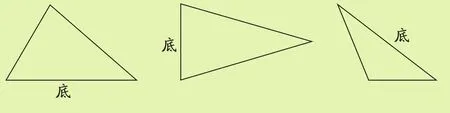
[分析与解]根据题意,可以利用三角板上的两条直角边来画高。以题中第一幅图为例,首先将三角板上的一条直角边与三角形的底重合(如下图),然后沿着底的方向平移三角板,直到另一条直角边经过底所对的顶点,再从这个顶点向相对应的底画垂直线段,这条从顶点到垂足之间的线段就是需要画的高,注意标注直角符号。

另两个三角形高的画法如下:
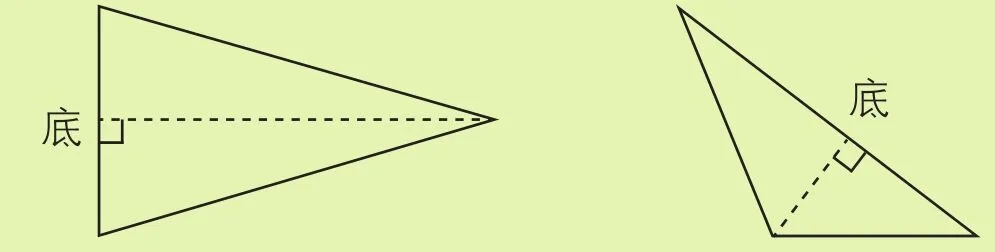
二、三角形的分类及解题方法
根据三角形角的特点,可以将三角形分为锐角三角形、钝角三角形和直角三角形。由三角形边的特点可知,两条边相等的三角形是等腰三角形,三条边相等的三角形是等边三角形。
例3.一根铁丝长30厘米。用这根铁丝围成一个等腰三角形,其中一条边的长度为12厘米,这个三角形的另两条边的长度分别是多少厘米?

[分析与解]题中没有明确说明长12厘米的边是这个等腰三角形的腰或底。可以分类考虑:如果长12厘米的边是这个等腰三角形的腰,则另一个腰的长度也是12厘米,底边的长度是30-12×2=6(厘米);如果长12厘米的边是这个等腰三角形的底,则一个腰的长度是(30-12)÷2=9(厘米)。因此,这个三角形的另两条边的长度可能是12厘米、6厘米,也可能是9厘米、9厘米。
例4.下面的三角形,按角分类分别是什么三角形?
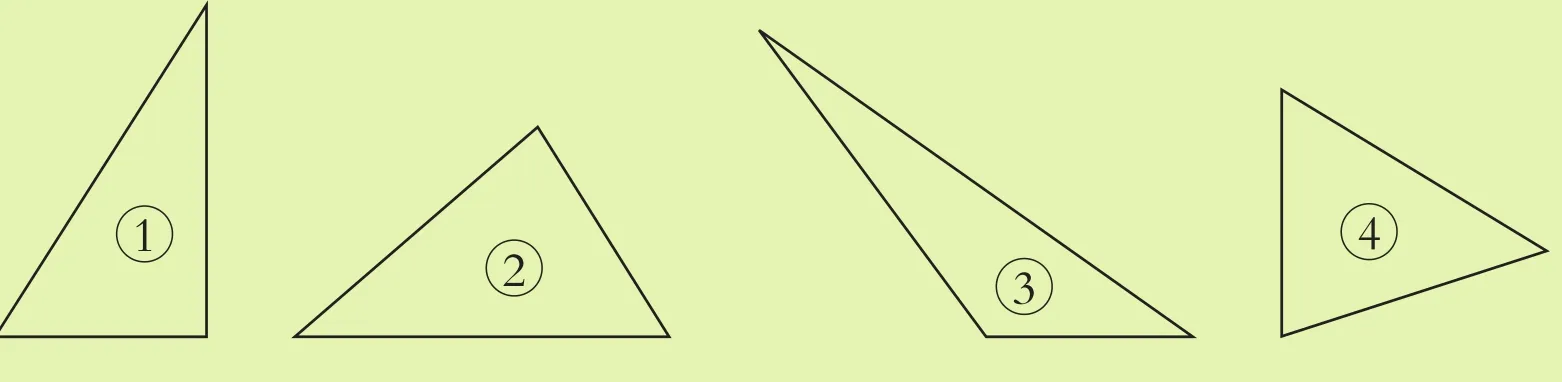
[分析与解]观察上面4个三角形,找出每个三角形的角的特点。有的三角形三个角都是锐角,这样的三角形叫做锐角三角形;有的三角形有一个角是钝角,其余两个角是锐角,这样的三角形叫做钝角三角形;有的三角形有一个角是直角,其余两个角都是锐角,这样的三角形叫做直角三角形。由此可得到,①号三角形是直角三角形,②号、④号三角形是锐角三角形,③号三角形是钝角三角形。
三、三角形的内角和及解题方法
三角形的内角和是180°,利用三角形的内角和是180°可以探究出四边形内角和是360°。进而可以得到:多边形内角和=(多边形的边数-2)×180°。
例5.等腰三角形的一个内角是50°,其他两个内角的度数各是多少?

[分析与解]题中没有明确说明已知的50°的角是这个等腰三角形的顶角还是底角。因此,50°的角可能是这个等腰三角形的顶角,也可能是等腰三角形的一个底角。
如果50°的角是这个等腰三角形的顶角,则根据角的特点,可求出它的一个底角的度数是(180°-50°)÷2=65°;如果50°的角是等腰三角形的一个底角,则根据角的特点,可求出它的顶角的度数是180°-50°×2=80°。所以其他两个内角的度数可能是65°、65°,也可能是50°、80°。

