从此岸到彼岸——《分数的意义》教学实录及赏析

姚晶晶 周卫东（特级教师）

【教学内容】

人教版五年级下册第45页。

【教学目标】

1.使学生初步理解单位“1”的含义，经历分数意义的抽象过程，进一步理解分数的意义。

2.使学生在建构分数意义的过程中，培养分析、综合、抽象、概括的能力。

3.使学生在解释分数于实际情境中所表示的意义等活动中，体会分数的应用价值。

【教学过程】

一、顺学而导，引入新知

师：这节课我们要研究什么内容？

生：分数的意义。

师：三年级时，我们两次学习分数，下面来检验一下同学们前面学得怎么样。

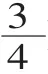
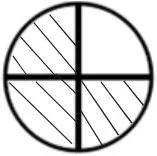
图1

图2

图3

师：（指图3）对于这幅作品，大家有什么比较好的建议？

生：用一个圈把这四个圆圈在一起，更容易看出“1”在哪。

师：这位同学的作品就有一个圈（出示图4），现在大家觉得怎么样？还有别的建议吗？

生：我认为分数首先要分。图4虽然看到了一个整体，但看不出分的痕迹。

师：我非常同意这位同学说的，分数首先要分，这张图（指图4）“分”了吗？哪位同学来修改，把它分一下。

（学生上展台修改图4，如图5）

图4

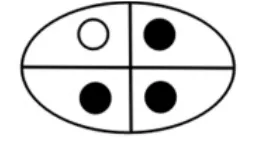
图5

师：说说你是怎么分的？

生：我把这四个圆平均分成4份。

师：在研究分数的过程中，有一个特别重要的前提是什么？

生：前提是要平均分。

师：平均分是研究分数的前提，没有平均分就没有分数。

二、比较探究，逐步抽象

1.第一次概括：抽象出单位“1”。

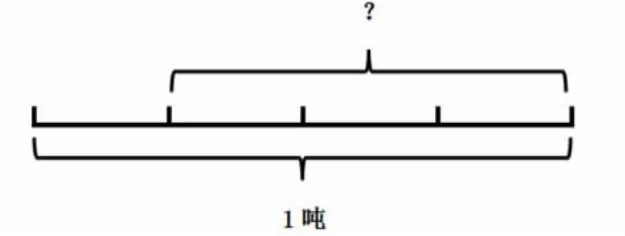
图6

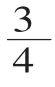
生：都是把一个整体平均分成4份，取其中3份。

师：善于比较、求同存异是学习数学的一项重要的基本功。大家再比较一下，图1、图5、图6有什么不一样的地方呢？

生∶图6是线段图，图1和图5都不是线段图。

生：图1分的是一个物体。（板书“一个物体”）

师：那图5呢？

生：图5分的是4个物体。

师：分的物体只能是4个吗？画8个行不行？画10个呢？

生：可以。

师：图5可以怎么概括？

生：把多个物体平均分成4份。（板书“多个物体组成的一个整体”）

师：图6中的这条线段代表什么呢？

生：质量单位。

师：如果把这里的1吨换成1米、1小时、1平方米行不行？

生：可以！

师：谁能说说这条线段可以代表什么？

生：一个计量单位！（板书“一个计量单位”）

师：一个物体、一个计量单位和多个物体组成的一个整体，都被叫做单位“1”。

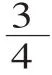
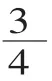
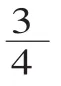
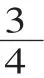
3.第三次概括：抽象出分数的意义。

PPT出示：

师：每个句子里的单位“1”是什么？分数表示什么含义？

生：第二句把地球表面面积看作单位“1”，平均分成100份，海洋面积是其中的71份。

师：这句话里面还隐含了另外一个分数，你能感觉到吗？

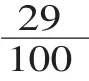
生：第三句是把1小时看作单位“1”，平均分成3份，小明做作业用了这样的1份。

师：同学们能不能概括一下，究竟什么是分数呢？

生：把单位“1”平均分成 X份，表示其中的N份。

师：这位同学有很强的符号意识，如果用文字来表示呢？

生：若干份。（板书“若干份”）

师：表示这样的N份，用什么词好呢？

生：1份或几份。

师：你是怎么知道的？

生：因为把单位“1”平均分成若干份，表示的可以是1份也可以是几份。

师：反思、回顾一下，我们是怎么概括出分数的意义的？

生：先学习了什么是单位“1”的意义。

生：研究了图1、图5、图6三幅图中的变与不变。

生：在研究了四个具体分数的意义之后，概括出了分数的意义。

师：说得太好了！我们是以“变”与“不变”为线索，研究出了分数的意义。

三、拓展延伸，意义建构

1.分一分。

PPT出示：

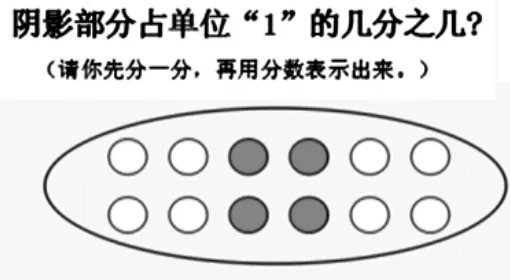
师：这里的单位“1”有12个圆片，其中有一部分涂了颜色，请你先分一分，再用分数表示出来。

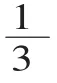
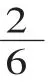
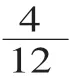
师：比较三位同学的分法，什么变了，什么没变？

生：第一位同学是把单位“1”平均分成3份，阴影部分表示这样的1份；第二位同学是把单位“1”平均分成6份，阴影部分表示这样的2份；第三位同学是把单位“1”平均分成12份，阴影部分表示这样的4份。

师：那什么地方不变呢？

生：单位“1”没变，阴影部分的数量也没变。

师：同样的单位“1”，不同的分法就能得到不同的分数。谁还有进一步的发现？

生：分的份数越多，每一份代表的数就越小。

生：这三种分法中阴影部分没变，三个分数的大小应该是相等的。

2.游戏。

师：同学们，分圆片中有变与不变，游戏中也有变与不变呢！

（1）游戏一：按要求取物。

（出示A、B两个袋子，每袋各装有一些圆片，分别发给两位学生）

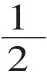
（A袋学生贴出5个，B袋学生贴出3个）

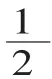
生：两个袋子的单位“1”不一样。

师：大家算一算，A袋单位“1”是多少？B袋单位“1”是多少？

生：A袋10个，B袋6个。

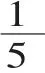
（A、B两位学生分别摆出2个圆片）

师：同学们看一下他们的结果，如果你是数学老师，你可能会问一个什么数学问题？

生：为什么分数不一样，拿出的个数却是一样的呢？

师：谁能回答这个问题？

生：因为它们的单位“1”不一样。

小结：不一样的单位“1”，不一样的份数，但是它们取出的个数可能是一样的。

（2）游戏二：挑战未知。

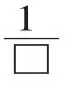
师：把刚才A、B两个袋子里的16个圆片都摆在一起，成为一个大的单位“1”。

师：如果要你取圆片，你打算取几个？方框里填几？

（学生汇报略）

师：谁能看出，这两个游戏里的变与不变呢？

四、回顾反思，全课总结

师：同学们，通过这节课的学习你有哪些收获呢？

……

【赏析】

仰慕周老师已久，终于有机会近距离聆听周老师的《分数的意义》，周老师的精彩课堂成为我们所有教师难忘的精神大餐。

《分数的意义》这一内容并不好教：一是知识点较多，诸如单位“1”、分数的意义、分数单位等，还有不同教师在理解这一内容的一些“增殖”目标；二是内容较为抽象，本课教学正逐步剥离具体素材的依附，实现分数从“面积模型”到“集合模型”的过渡，并在此过程中进行“数学化”提炼，形成纯理论的表达；三是时间跨度相隔较长，人教版、苏教版都是分别在三年级上册、三年级下册两次安排了《分数的初步认识》的学习，而《分数的意义》的学习则安排在五年级下册，离前两次相关内容的学习已有了一年半之久。

如上这些“不好教”的因素被周老师一一化解。细细品味周老师的课堂，深深地感到：儿童数学学习的过程，是一个不断地触摸知识本质的过程，是一个经验激活、思维引发、思想萌芽的过程，总之，是一段经由此岸到达彼岸的难忘航程。

一、此岸有“点”：准确地找到知识的生长点与学情基点

二、航程有“人”：引领学生充分经历知识的形成过程

三、彼岸有“景”：驶向思维、思想的纵深处

周卫东老师一直倡导一个观念：教学，不能囿于抵达，更要能远航！本节课的教学，在概括了分数的意义之后，学生思维的脚步并没有停下，而是在多层问题情境的作用下不断发酵、孕育与生长。“分12个圆片”的设计，引导学生于“变”与“不变”的辩证思维中感悟在总数不变的情况下，分的份数与每份数的大小变化、分子分母的变化与分数值大小关系等等，为后续分数基本性质的学习做了很好的铺垫，感受到分数的多种联系和规律，意识到数学知识的意蕴与深刻。“游戏”两个环节的设计，把学生的思维不断引向纵深，两环节隐含了众多的思维发散点，更是指向分数问题的解决。学生在激烈的思维燃烧、智慧碰撞中，延伸、拓展对于分数内涵的深刻理解，逐步完善分数知识的意义建构。