度量加权直觉模糊序信息系统的粗糙隶属度

杨 倩， 徐伟华， 林冰雁

(重庆理工大学 理学院 重庆 400054)

0 引言

作为知识处理的重要工具，粗糙集理论[1]较其他方法更适合用来处理信息系统中的不确定性问题，并且不会用到任何所需处理数据之外的先验知识．在处理模糊性等方面的信息时，直觉模糊集[2-4]相较于模糊集[5]更加全面、有效．不少学者越来越关注粗糙集和直觉模糊集的融合与互补，已被应用于决策分析[6]、知识获取[7]、医疗诊断、逻辑规划、模式识别[8]、机器学习[9]和市场预测[10]等诸多领域．

目前，对直觉模糊序信息系统的研究已颇为成熟．文献 [11]介绍了直觉模糊环境下的序信息系统，通过准则集定义了直觉模糊信息系统中的优势关系，即根据属性的准则对它进行排序，并探究了其相关性质．决策者在做决策时往往仅考虑专家依据经验给出的隶属度、非隶属度和犹豫度，看似解决了经典信息系统中所需数据过于精确的问题，实则降低了数据的客观性，并使结果的准确性受到了质疑．现实生活中常需要做出正面或负面的决策，做出决策时还需要考虑各种因素，而各因素的偏好程度又有所不同．本文提出了度量加权直觉模糊序信息系统，更适用于探究各类涉及主观判断的实际问题．其优势在于做正面决策时可以着重考虑各因素隶属度的取值，做负面决策时可以更侧重于非隶属度的取值.因此，可以根据不同偏好程度取定度量加权向量对优势类进行优化，进而使结果与实际生活更加贴切．同时，定义了这一背景下的粗糙隶属度[12]及其相关性质，并通过实例验证了该模型的可行性和有效性．

1 预备知识

传统模糊集理论中的隶属度刻画了“非此即彼”的现象，而直觉模糊集在一定程度上克服了这一难点，增加了非隶属度和犹豫度函数，使其可以形象地表示“亦此亦彼”的情形，在一定程度上提高了描述的准确性．为了方便理解，下面先给出一些相关基本概念．

定义1[11]设三元组I=(U,C,F)为信息系统，U={x1,x2,…,xn}是非空有限对象集，C={a1,a2,…,am}是有限条件属性集，F={f:U→Va,a∈C}是U与C的关系集，其中Va为条件属性a的有限值域.若对∀a∈C,f∈F,x∈U，都有

f(x,a)=〈x,μa(x),νa(x)〉，

其中：函数μa:U→[0,1]和函数νa:U→[0,1]分别表示U中元素x在条件属性a下的隶属度和非隶属度,并且满足0≤μa(x)+νa(x)≤1，则称I=(U,C,F)为直觉模糊信息系统．通常用IF(U)表示论域U上直觉模糊集的全体．

定义2[13]设I=(U,C,F)为一个直觉模糊信息系统，∀x∈U，∀a∈C，定义一个度量加权向量ω=(ω1，ω2，ω3)，其中ω1、ω2、ω3分别为隶属度和非隶属度以及犹豫度的权重，且度量加权系数满足ω1+ω2+ω3=1(0≤ωi≤1,i=1,2,3)．定义对象x对属性a的度量加权得分函数为

Δa(x)=ω1μa(x)-ω2νa(x)-ω3πa(x)，

其中：πa(x)=1-μa(x)-νa(x)，表示对象x在属性a下的犹豫度．

注：当评价者越看重隶属度时，ω1的取值越大；当评价者越看重非隶属度时，ω2的取值越大；当评价者越看重犹豫度时，ω3的取值就越大．所以在进行得分评价时，可以根据实际需求给出相应的权重．由于ω1+ω2+ω3=1，那么在取值时只需给出权重ω1和ω2，并保证ω1+ω2≤1即可．

定义3[13]设I=(U,C,F)为一个直觉模糊信息系统，对∀f∈F，∀a∈C，∀xi,xj∈U，都有

f(xi,a)≥f(xj,a)⟺Δa(xi)≥Δa(xj).

根据加权得分函数，在属性a的值域上存在着递增偏序关系“≥”或递减偏序关系“≤”．在直觉模糊决策信息系统中，如果某个属性的值域为递增的偏序或递减的偏序，那么称该属性是直觉模糊决策信息系统中的一个准则，并且由若干准则组成的集合叫做准则集．

定义4[11]设I=(U,C,F)为一个直觉模糊信息系统，若直觉模糊信息系统I中所有的属性都为准则，对∀a∈C，f∈F，xi,xj∈U，满足：

f(xi,a)≤f(xj,a)⟺[μa(xi)≤μa(xj),νa(xi)≥νa(xj)]；

f(xi,a)≥f(xj,a)⟺[μa(xi)≥μa(xj),νa(xi)≤νa(xj)]，

则称I≥=(U,C,F)为直觉模糊序信息系统．下面通过具体的例子加以说明．

例1某学校为了对教师进行学年制综合评优，将影响10位教师评选结果的4个因素分别记为a1,a2,a3,a4,表1为相应的直觉模糊序信息系统．其中论域U={x1,x2,…,x10}，条件属性C={a1,a2,a3,a4}，显然，对∀a∈C,f∈F,x∈U，都有f(x,a)=〈x,μa(x),νa(x)〉,并且满足：

f(x1,a1)≥f(x2,a1)⟺[μa1(x1)≥μa1(x2),νa1(x1)≤νa1(x2)]；

f(x1,a2)≤f(x2,a2)⟺[μa2(x1)≤μa2(x2),νa2(x1)≥νa2(x2)]，

其余各f(xi,a)之间的关系依此类推.

2 度量加权直觉模糊序信息系统

为了使研究直觉模糊集序关系的过程变得更简单，引入度量加权的概念来描述基于直觉模糊集的度量加权直觉模糊序信息系统．

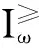
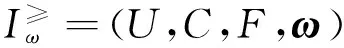
(y),∀a∈A}.

(x),∀a∈A}，

其中Δa(x)=ω1μa(x)-ω2νa(x)-ω3πa(x)，是对象x对属性a的度量加权得分函数，并且ω1+ω2+ω3=1．

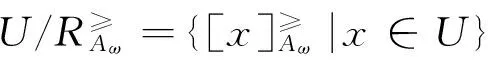
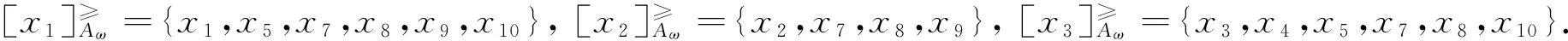
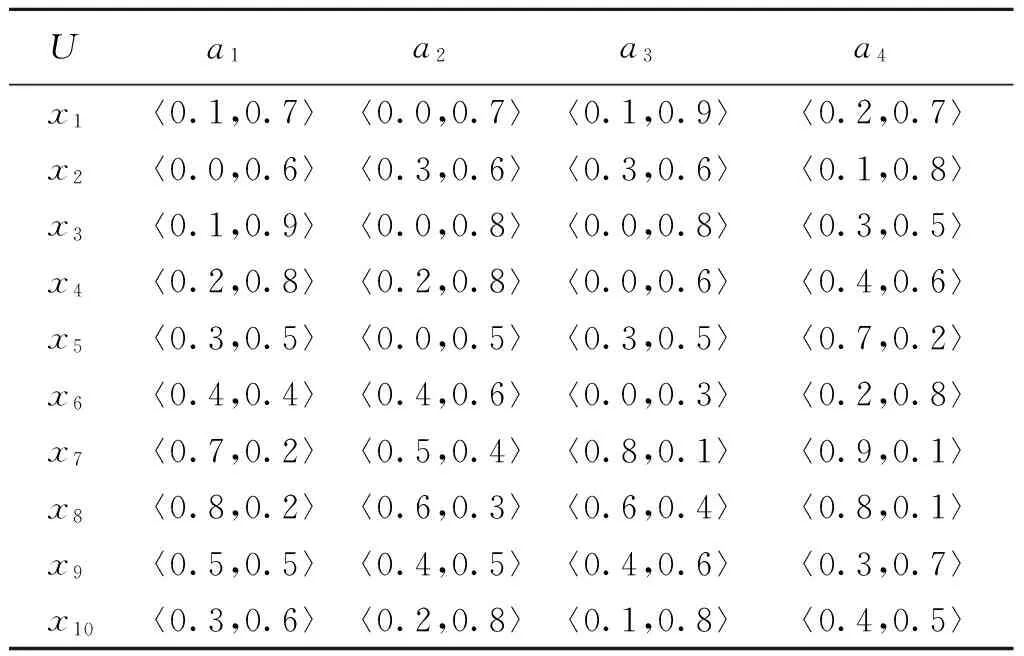
表1 直觉模糊序信息系统

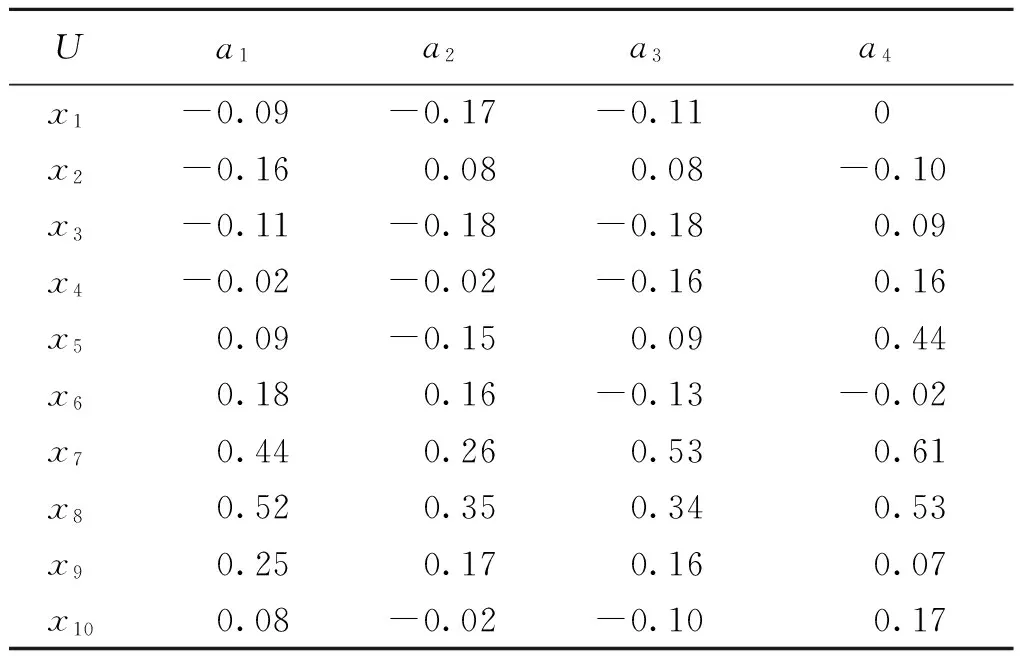
表2 度量加权得分序信息系统

3 度量加权直觉模糊序信息系统中粗糙集的粗糙隶属度

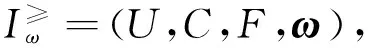
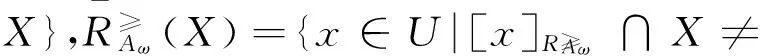
性质1X的上、下近似具有以下性质：

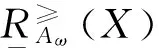
证明这里仅对下近似进行证明．

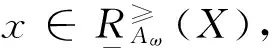
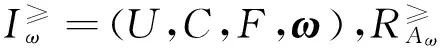
接下来讨论度量加权直觉模糊序信息系统中粗糙集的粗糙隶属函数的性质.

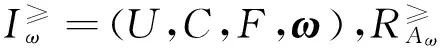
粗糙隶属度具有以下性质.

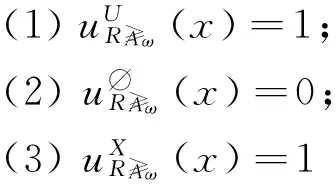
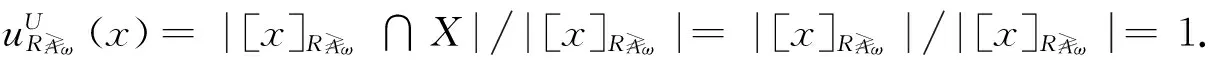
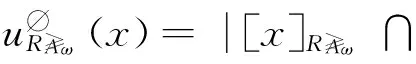
(5) 由(3)和(4)可以得以验证．

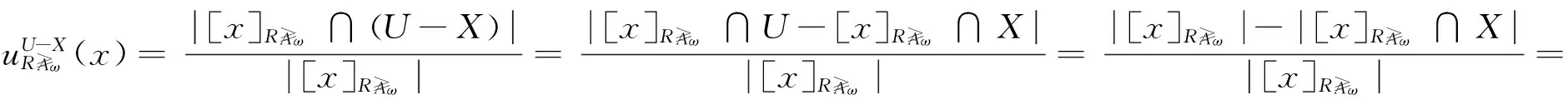
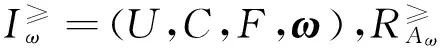
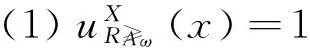
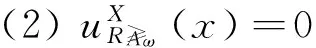
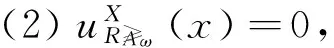
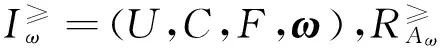
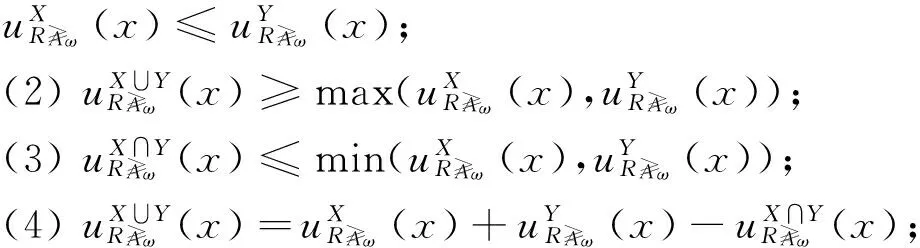
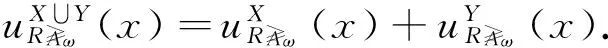
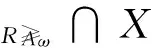
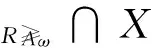
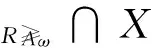
(4) 根据定义9，有

(5) 由于X∩Y=∅，所以可以根据(4)证明出结论．

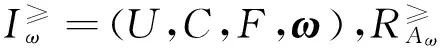
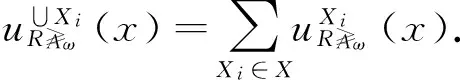
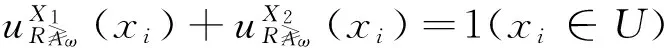
4 实例分析

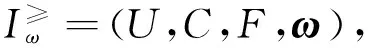
考虑到度量加权向量ω=(0.3,0.5,0.2)，根据度量加权得分函数的定义，把表3转化为如表4所示的度量加权得分序信息系统，再根据度量加权直觉模糊优势类的定义可得

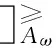
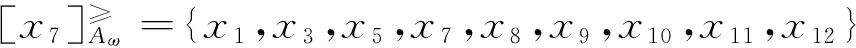
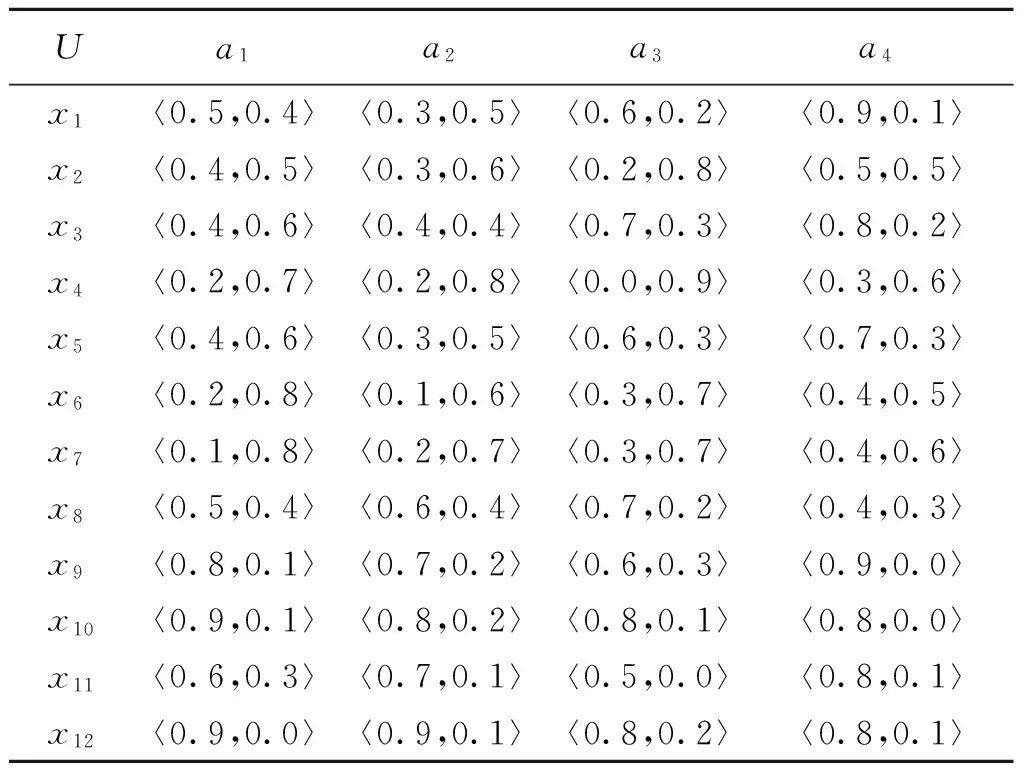
表3 某服装公司的直觉模糊序信息系统

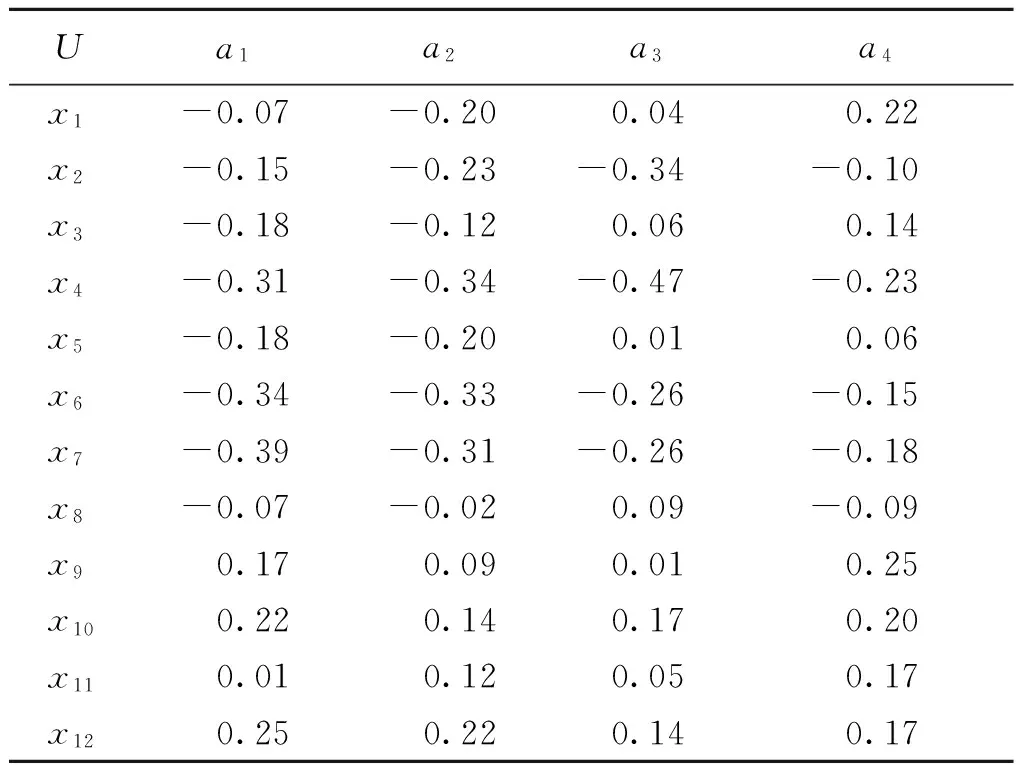
表4 某服装公司的度量加权得分序信息系统

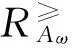
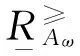
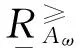
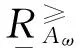
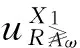
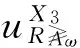
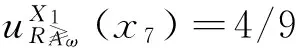
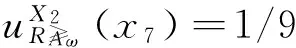
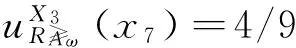
5 结束语

在引进度量加权直觉模糊序信息系统的基础上，重点探究了度量加权直觉模糊序信息系统中粗糙集的粗糙隶属度，进而对粗糙隶属度进行了公理化研究．基于加权直觉模糊集的直觉模糊序信息系统的研究克服了直觉模糊序信息系统研究过程中的局限性.本文虽然对各属性之间加权处理的情形进行了讨论，但并没有对属性和属性之间的权重予以考虑．而由于不同对象之间的相互影响以及不同对象对不同影响因素存在各种主观判断，所以不仅应该对属性进行加权，属性和属性之间也应该进行加权处理后再深入探讨．因此，下一步工作将对此问题进行更深入的探索．

参考文献：

[1] PAWLAK Z．Rough sets：theoretical aspects of reasoning about data[M]．Boston：Kluwer Academic Publishers，1991．

[2] 刘华文．直觉Fuzzy集的基本定理[J]．工科数学，2000，16(1)：55-60．

[3] 雷英杰，王宝树，胡军红．直觉模糊等价矩阵构造方法[J]．系统工程理论与实践，2007,27(7):127-131.

[4] 徐泽水．直觉模糊信息集成理论及应用[M]．北京：科学出版社，2008．

[5] 张小红，裴道武，代建华．模糊数学与Rough集理论[M]．北京：清华大学出版社，2013．

[6] 张爱平，张小红．一种应用Rough集的多属性决策方法[J]．计算机工程与应用，2009,45(30):220-223.

[7] 张文修，梁怡，吴伟志．信息系统与知识发现[M]．北京：科学出版社，2003．

[8] 王珏，苗夺谦，周育健．关于Rough set理论与应用的综述[J]．模式识别与人工智能,1996,9(4)：337-344．

[9] 周志华．机器学习[M]．北京：清华大学出版社，2016．

[10] 朱永明．基于粗糙集理论的股市预测研究[J]．郑州大学学报(理学版),2009，41(4):40-44．

[11] 徐伟华．序信息系统与粗糙集[M]．北京：科学出版社，2013．

[12] 徐伟华，刘士虎，张文修．一般二元关系下基于粗糙隶属函数的程度粗糙集[J]．重庆理工大学学报(自然科学版)，2010，24(10)：101-108．

[13] 胡猛，郭艳婷，徐伟华．优势关系下直觉模糊信息系统的变精度与程度“逻辑或”粗糙集[J]．运筹与模糊学，2016，6(2)：66-77．