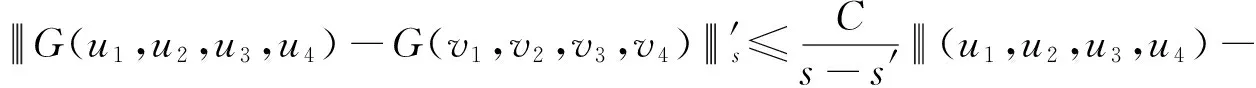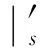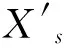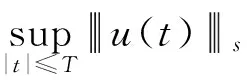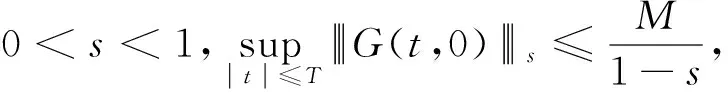两分支Novikov系统Cauchy问题解的解析性

张 丽， 高娟娟

(1.西北大学 数学学院 陕西 西安 710127； 2.西北大学 非线性科学研究中心 陕西 西安 710069)

0 引言

考虑两分支Novikov系统Cauchy问题：

(1)

其中：t>0;x∈R；m=u-uxx. 文献[1]首先提出了带有1个哈密顿结构模型的两分支Novikov系统.当式(1)中ρ=0时，该系统就变为Novikov方程，文献[2]证明了该方程拥有双哈密顿结构和守恒量的无穷序列.文献[3]证明了该模型解的局部适定性和爆破条件，利用守恒律为该系统提出了两个爆破条件.目前还有很多学者对方程解的解析性进行了研究，比如两分支Camassa-Holm系统[4]、两分支b-family系统[5]等.

以两分支Novikov系统解的局部适定性为基础，接下来证明式(1)的Cauchy问题解的解析性.

1 解析性的证明

现将初值问题(1)转化成下面的非局部形式：

(2)

其中：t>0；x∈R；u0，ρ0∈Cω(R).

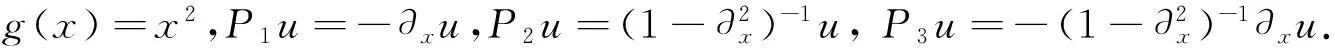
∂tρ=-g(u)P1ρ-ρuP1u,

接下来，令u1=u,u2=P1u,u3=ρ,u4=P1ρ，可得

∂tu3=-u4g(u1)-u1u2u3≡G3(u1,u2,u3,u4)，∂tu4=-P1[u1u2u3+u4g(u1)]≡G4(u1,u2,u3,u4).

因此可把初值问题(1)转化为：

(3)

定义U≡(u1,u2,u3,u4)和G(U)=G(u1,u2,u3,u4)≡(G1(u1,u2,u3,u4),G2(u1,u2,u3,u4),G3(u1,u2,u3,u4),G4(u1,u2,u3,u4)).得到

(4)

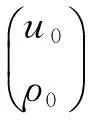
为了证明定理1，需要定义一个如下的合适度量Banach空间，对任意s>0，定义

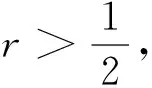
引理1[6]令00,使得对任意的函数u,v∈Ys，有

uvs≤Cusvs，这里C=C(r)仅依赖r.

对任一s>0，任意的u,v∈Ys，g(u)=u2，下面的结论成立.

g(u)-g(v)s=u2-v2s≤Cu+vsu-vs.

引理2[6]对任一0

用以上两个引理来对定理2证明.

证明对任意uj,vj∈B(0,R)⊂Ys(j=1,2,3,4),得到

分别对A1、A2、A3、A4来做估计.

接下来用以上方法，依次来估计A2,A3,A4，得到：

定理1可由Cauchy-Kowalevski定理得出.

s.探讨方程的Cauchy 问题：

(5)

令T,R与C都是正数，并假设式(5)中的函数G满足下面的3个条件：

2) 对任意的0

当方程组(3)或(4)变成方程组(5)的零初值条件时，定理3中的条件1)和3) 很容易得到证明.由定理2可知，方程组(3)或(4)满足定理3中的条件2).从而方程组(3)或(4)满足了定理3中的3个条件，因此就证明了两分支Novikov系统Cauchy问题的解关于空间变量是全局解析的，关于时间变量是局部解析的.即定理1就得到了证明.

参考文献：

[1] POPOWICZ Z. Double extended cubic peakon equation[J]. PHYS LETT A, 2015, 379(18-19): 1240-1245.

[2] HONE A N W, WANG J P. Integrable peakon equations with cubic nonlinearity[J]. J PHYS A： MATH THEOR, 2008, 41(37): 4359-4380.

[3] LUO W, YIN Z. Local well-posedness and blow-up criteria for a two-component Novikov system in the critical Besov space[J]. Nonlinear analysis, 2015, 122: 1-22.

[4] 郑晓翠, 高晓红. 两分支Camassa-Holm系统Cauchy问题解的解析性[J]. 西北大学学报 (自然科学版), 2016, 46(2): 14-18.

[5] LIU J, YIN Z. On the Cauchy problem of a two-component b-family system[J]. Nonlinear analysis real world applications, 2011, 12(6): 3608-3620.

[6] YAN K, YIN Z. Analytic solutions of the Cauchy problem for two-component shallow water systems[J]. Mathematische zeitschrift, 2011, 269(3/4): 1113-1127.

[7] HIMONAS A A, MISIOLEK G. Analyticity of the Cauchy problem for an integrable evolution equation[J]. Mathematische annalen, 2003, 327(3): 575-584.