径向力对螺旋离心泵转子系统动力学响应的影响

袁丹青, 王 航, 丛小青, 季 明, 张 楠

(江苏大学 能源与动力工程学院, 江苏 镇江 212013)

螺旋离心泵自20世纪60年代初被M.STHALE发明以来,其应用范围不断扩大.单叶片螺旋离心泵具有独特的螺旋扭曲叶片,使得其具有无堵塞性好、无损性能好等优点.但是由于叶轮几何结构不对称,造成其动平衡特性较差,在运行时泵的振动问题较为严重,限制了其向高速化的发展.

泵转子系统的振动一直都是学者们研究的一个关键问题,取得了很多成果[1-5].但是对螺旋离心泵的研究大多集中在叶轮的设计方法[6-7]和流场分析[8-9],转子系统振动问题研究相对较少[10-11],因此,研究螺旋离心泵转子系统的动力学特性对确保产品稳定、可靠、安全运行具有重要意义[12].

文中利用CFX14.5对螺旋离心泵在不同工况下所受的径向力进行计算和分析,并将径向力作为转子系统的外部激励力,利用专业转子动力学分析软件samcef rotor对单叶片螺旋离心泵转子系统进行临界转速、模态振型和瞬态响应分析,为螺旋离心泵转子系统的优化设计提供参考.

1 模型参数

以一台单叶片螺旋离心泵为研究对象,设计参数为流量Q=200 m3·h-1,扬程H=32 m,转速n=1 480 r·min-1,效率η=65%.叶轮几何参数为进口直径D1=160 mm,出口直径D2=386 mm,出口宽度b2=66.5 mm,叶轮形式为半开式.叶轮材料为HT250,密度为7 280 kg·m-3,弹性模量为138 GPa,泊松比为0.156.轴材料是45钢,密度为7 890 kg·m-3,弹性模量为209 GPa,泊松比为0.269.流体区域模型如图1a所示,固体区域模型如图1b所示.

图1 流场和结构场示意图

2 径向力计算与分析

2.1 数值模拟方法

利用ANSYS 14.5 ICEM对流体区域进行网格划分,生成四面体非结构化网格,总数为1 335 333.流场计算在CFX 14.5中进行,先进行定常计算,湍流模型采用标准k-ε模型,由于存在动、静2种计算域,故采用多重参考坐标系MRF,动静交界面的坐标系变换设置为frozen rotor.边界条件采用速度进口、开放式出口、固体壁面设置为无滑移边界.设置对流项的求解格式为高阶求解格式,湍流数值项的求解格式为一阶格式,求解总步数为3 000,时间尺度为物理时间尺度,叶轮每旋转3°为一个时间步长,时间步长为0.000 337 8 s,残差收敛精度为10-4.在定常计算收敛的基础上,把计算结果作为非定常计算的初始条件,动静交界面的坐标系变换设置为transient rotor stator,设置非定常计算总计算时间为10个叶轮旋转周期,即0.405 4 s,同时监测作用在叶轮上随时间变化的径向力,其他设置和定常计算设置相同.

2.2 计算结果及分析

图2为变流量工况下叶轮所受径向力的时域图,从图中可以看到叶轮所受的径向力呈周期性变化,径向力的周期和叶轮旋转一周所用的时间相同.设计工况下叶轮所受径向力的最大值相对较小,偏离设计工况越远,叶轮所受径向力的最大值越大,在同一个周期内叶轮径向力的变化幅度也越大.在同一个周期内,小流量工况下和大流量工况下径向力最大值出现的相位差为180°,即小流量工况下和大流量工况下最大径向力的方向相反.综合各工况下的径向力来看,径向力的数值比普通的轴对称离心泵大,主要原因是叶轮与蜗壳耦合面上的压力分布不均匀,使叶轮所受径向力较大.

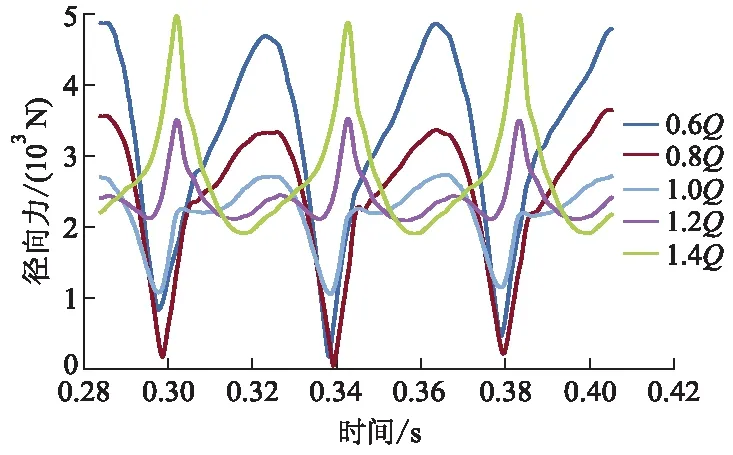
图2 径向力时域图

经过快速傅里叶变换,得到如图3所示的不同流量工况下径向力的频域图.由图可以看出,径向力由恒定量和脉动量叠加而成.在设计工况下的恒定力最小,偏离设计工况越远,恒定力越大.不同流量工况下径向力脉动的主频均为叶轮转动的频率,在1.2倍设计流量下的主频最小.脉动峰值出现在叶频及其倍频处,随着频率的增加,脉动峰值逐渐减小.

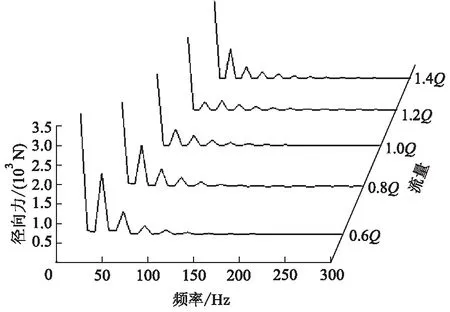
图3 径向力频域图

3 临界转速计算与分析

3.1 数值模拟

将转子模型导入samcef rotor中,选择critical speed & stability模块进行临界转速和振型的计算.把动力学参数输入有限元模型中,在轴承处施加约束,根据相关手册[13-14],在ground bearing中设置轴

承的刚度系数为Kxx=Kyy=151 343 N·mm-1.当系统做自由振动时,求解系统的固有频率和模态振型,阻尼的影响较小,可忽略阻尼力.对叶轮和轴均采用四面体网格划分,网格总数为34 019.临界转速的计算方法选择伪模态法(Pseudo-Modal),扫频范围为0～800 Hz,扫频次数为128,输入特征值为10.

3.2 计算结果与分析

转子的固有频率是指转子做正向涡动时的频率,通常情况下,水泵转子系统的运行转速较低,故只对前4阶涡动频率进行分析,如表1所示.由表可以看出,随着阶次的增加,涡动频率也逐渐变大,转子1阶正向涡动频率为105.66 Hz,即6 339.6 r·min-1,远远大于本模型在设计条件下的转速1 480 r·min-1,可见转子属于刚性转子,在设计条件下不会发生共振,运行情况较为平稳.

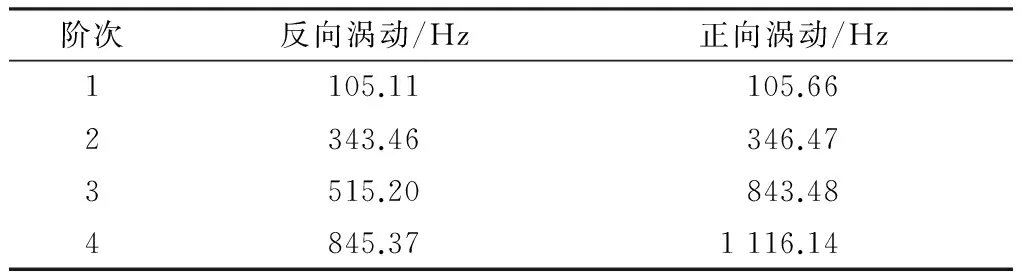
表1 前4阶涡动频率

一般情况下,转子-轴承系统在运行时做正向涡动运动,并且低阶固有振型对转子结构振动的影响比高阶固有振型大,故只对转子系统做正向涡动时的前4阶模态振型进行分析,结果如图4所示.

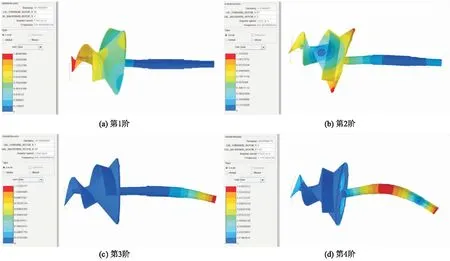
图4 各阶模态振型

从图4可以看出,第1阶和第2阶振型主要表现为叶轮的弯曲变形,第1阶振型中,变形最大的地方出现在叶片的进口处,而在第2阶振型中,变形最大的地方出现在叶轮的外缘处.第3阶和第4阶振型主要表现为转轴的弯曲变形,第3阶振型表现为驱动端轴段的变形,第4阶振型中转轴中段的弯曲变形最为严重,叶片进口和轮毂后盖板处也发生了变形.

4 瞬态响应计算与分析

4.1 数值模拟

进行瞬态响应分析时,将计算类型设置为transient response,将轴的转速设为1 480 r·min-1,将径向力作为外部激励添加到叶轮表面上,在求解设置中监测叶轮进口与轴线交点处的位移随时间的变化,求解时间为0～30 s,时间子步数设置为111 000,即叶轮旋转一圈对应的时间步数为150.

4.2 计算结果与分析

在不考虑流体激励力的作用时,对转子系统进行瞬态响应分析,结果如图5所示,从图可以看出,监测点处的振动幅度较大,这是由叶轮结构不对称而产生的不平衡力所致,因此,要对叶轮进行适当的配重,减小叶轮的偏心情况.

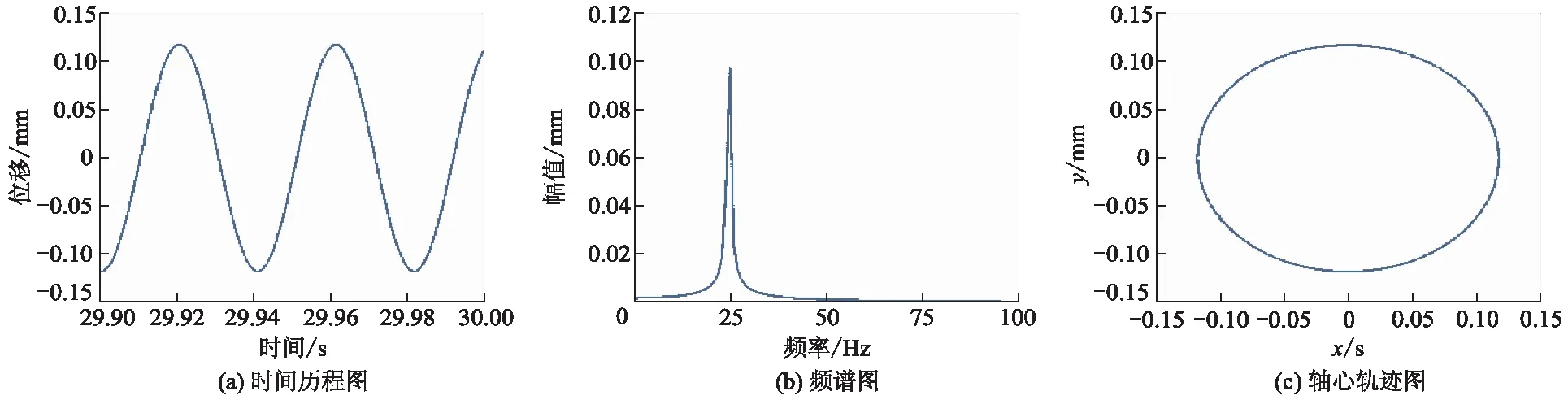
图5 无流体激励力下的响应

当考虑叶轮所受的径向力对转子系统瞬态响应的影响时,结果如图6所示.

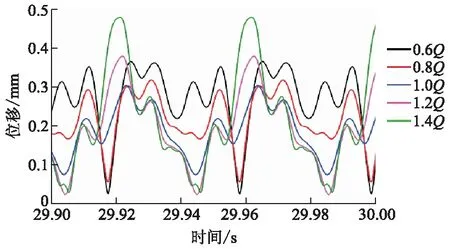
图6 不同流量工况下的时间历程图

从图6可以看出,监测点的振动情况比较复杂.在设计工况下,监测点的振动幅度较小,偏离设计工况越远,振动幅度越大,大流量工况下的振动幅值大于小流量工况下的振动幅值.在同一个周期内,大流量工况下最大位移出现的时刻与小流量工况并不相同,二者存在一定的相位差.

经过快速傅里叶变换,得到如图7所示的不同流量工况下径向位移的频谱图.从频谱图上可以看出,振动的频率成分较为丰富,其中零频率分量所占的比例最大,即叶轮有较大的静位移,这是由于径向力中存在较大的恒定值,使叶轮产生了静挠度.在设计工况下,零频率分量的数值最小,偏离设计工况越远,数值越大.响应峰值出现在叶轮旋转频率及其倍频上,和径向力的频率相同,这说明径向力的频率成分会在转子的振动过程中表现出来,同时,振动主要集中在低阶倍频上,高阶分量所占的比例几乎为零.在设计工况和大流量工况下,主频为轴频,而在小流量工况下,主频为轴频的2倍频.这是因为叶轮因结构不对称而产生的不平衡力与小流量工况下径向力主频分量的相位差大于90°,两者叠加之后,使该频率下的合力较小,减小了该频率下的位移分量,使主频变成了轴频的2倍频.而在大流量工况下,两者的相位差小于90°,经过叠加之后,使该频率下的合力变大,增大了该频率下的位移分量.因为4倍频接近转子系统的第1阶固有频率,使该频率下幅值所占的比例变大,因此,可对转轴结构进行调整,使第1阶固有频率远离低阶倍频.

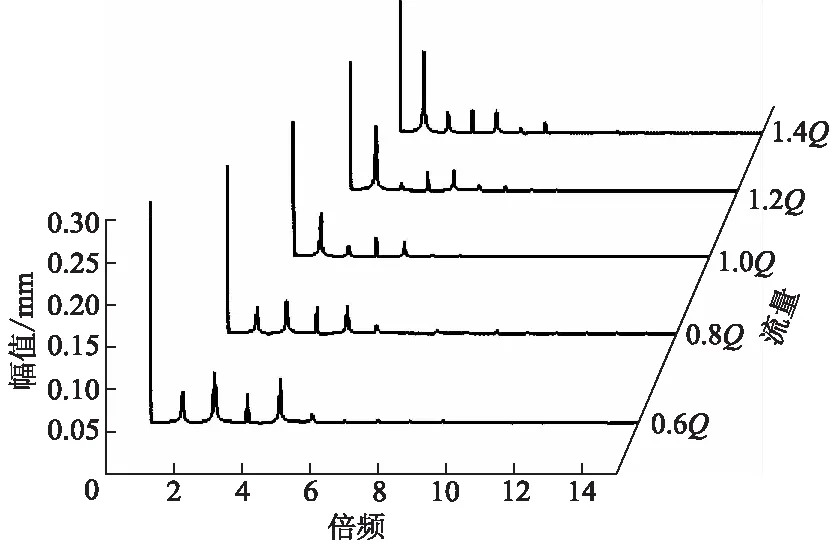
图7 频谱图

不同流量工况下的轴心轨迹如图8所示,从图可以看出,轴心轨迹较为复杂,这也反映了时间历程图的复杂性和频率成分的丰富性.在小流量工况和设计工况下,轴心轨迹主要偏向于第1和第4象限,在大流量工况下,轴心轨迹主要偏向于第4象限,轴心轨迹的差异主要是因为不同流量工况下叶轮所受的径向力不同,在和叶轮因结构不对称而产生的不平衡力共同作用后所产生的结果.

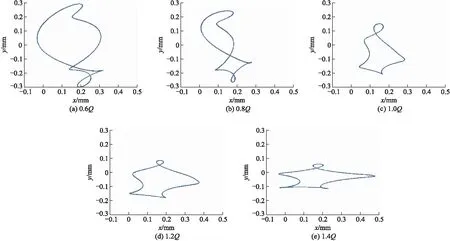
图8 不同流量工况下的轴心轨迹

5 结 论

1) 不同流量工况下,叶轮的径向力均呈周期性变化,周期和叶轮旋转的周期相同.设计工况下叶轮所受径向力的最大值相对较小,小流量工况下和大流量工况下径向力最大值的方向相反.径向力可以分解为恒定量和脉动量,随着频率的增加,脉动峰值逐渐减小.

2) 在设计转速下,转子系统不会发生共振,运行情况较为平稳.转子系统的前4阶模态振型均为弯曲变形,但变形情况各不相同.

3) 在不考虑径向力的作用时,监测点振动的频率和叶轮旋转的频率相同.当考虑径向力对转子系统瞬态响应的影响时,转子振动过程中会体现出径向力的频率成分.可对转轴结构进行适当调整,使第1阶固有频率远离低阶倍频,或采用双叶片对称布置来增加转子系统运行的稳定性.

参考文献(References)

[ 1 ] BENRA F K. Numerical and experimental investigation on the flow induced oscillations of a single-blade pump impeller[J]. Journal of Fluids Engineering, 2006, 128(4):783-793.

[ 2 ] ZHOU W J, WEI X S, WEI X Z, et al. Numerical analysis of a nonlinear double disc rotor-seal system[J]. Journal of Zhejiang University-Science A, 2014, 15(1):39-52.

[ 3 ] BERTEN S, DUPONT P, FABRE L, et al. Experimental investigation of flow instabilities and rotating stall in a high-energy centrifugal pump stage[C]∥Proceedings of the ASME 2009 Fluids Engineering Division Summer Meeting, 2009:505-513.

[ 4 ] 裴吉, 袁寿其, 袁建平,等. 基于虚拟仪器的离心泵振动测试系统设计[J]. 中国农村水利水电, 2010(3):132-135.

PEI J, YUAN S Q, YUAN J P, et al. Design of centri-fugal pump vibration test system based on virtual instrument[J]. China Rural Water and Hydropower, 2010(3):132-135.(in Chinese)

[ 5 ] 范福景. 单级离心泵振动分析研究[D]. 西安:西安石油大学,2013.

[ 6 ] 李仁年, 苏吉鑫, 韩伟,等. 螺旋离心泵叶轮叶片型线方程[J]. 排灌机械工程学报, 2007, 25(3):8-11.

LI R N, SU J X, HAN W, et al. Profile equations for impeller vane of screw centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2007, 25(3):8-11. (in Chinese)

[ 7 ] 敏政, 朱登魁, 戴雪兵,等. 基于速度系数法和型线方程相结合的螺旋离心泵叶轮设计方法[J]. 兰州理工大学学报, 2012, 38(4):48-50.

MIN Z, ZHU D K, DAI X B, et al. Design method of screw centrifugal pump impeller based on speed coefficient method and profile equations[J]. Journal of Lanzhou University of Technology, 2012,38(4):48-50. (in Chinese)

[ 8 ] TATEBAYASHI Y, TANAKA K, KOBAYASHI T. Pump performance improvement by restraining back flow in screw-type centrifugal pump[J]. Journal of Turbomachinery, 2005, 127(4):755-762.

[ 9 ] 张华, 陈斌, 施卫东,等. 单叶片螺旋离心泵内部流场数值计算及油膜试验研究[J]. 排灌机械工程学报, 2016, 34(5):381-385.

ZHANG H, CHEN B, SHI W D, et al. Numerical si-mulation and oil film observation on flow field in impeller of screw centrifugal pump with single-blade[J]. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34 (5): 381-385. (in Chinese)

[10] 徐宇平. 双叶片螺旋离心泵内部流动与转子两场耦合分析[D]. 镇江:江苏大学, 2012.

[11] YUAN S, LI T, YUAN J P, et al. Static stress and modal analysis on the impeller of screw centrifugal pump[J]. Iop Conference Series: Earth and Environmental Science, doi:10.1088/1755-1315/15/5/052013.

[12] 赵万勇, 白双宝, 马鹏飞. 离心泵转子振动研究现状与展望[J]. 流体机械, 2011, 39(3):37-39.

ZHAO W Y, BAI S B, MA P F. Research status and prospect of centrifugal pump rotor vibration[J]. Fluid Machinery, 2011,39 (3): 37-39. (in Chinese)

[13] 张松林. 最新轴承手册[M].北京:电子工业出版社, 2007.

[14] 付才高,郑大平,欧园霞,等.转子动力学及整机振动(航空发动机设计手册第19册)[M].北京:航空工业出版社,2000.