增程式电动汽车规则型能量管理策略对比

牛继高, 徐春华, 牛丹彤, 裴冯来

(1. 中原工学院 机电学院, 河南 郑州 450007; 2. 中国农业大学 信息与电气工程学院, 北京 100083; 3. 上海机动车检测认证技术研究中心有限公司, 上海 201805)

增程式电动汽车(extended-range electric vehicle,E-REV)的能量管理策略是整车控制的核心,直接关系到车辆的燃油经济性、动力性以及适应复杂工况的能力[1-2].E-REV的能量管理策略是目前的研究热点之一,可分为规则型和智能型2类.其中,基于规则的控制策略容易实现,根据相应的离线优化结果以及工程经验可作为实车的控制策略[3].目前,E-REV规则型能量管理策略主要包括恒温器策略[4-5]、多模式切换策略[6]、最优曲线策略[7]和功率跟随策略[8-9]等.

E-REV的能量系统包括动力电池和增程器,其中,增程器可采用多种形式,例如燃料电池[10-11]、发动机/发电机等.当采用发动机加发电机的形式时,前期的发动机功率匹配对能量管理策略的制定起着至关重要的作用,即由于发动机的峰值功率与其燃油效率最高点的功率不重合,因此发动机的选择有“大”和“小”之分.例如,当E-REV拟采用恒温器控制策略时,应匹配一台大功率的发动机,使其高效点的输出功率能够满足车辆所有设计工况的功率需求;相反,当最优点的输出功率不能满足所有设计工况的功率需求时,对应的发动机统称为小功率发动机.发动机峰值功率的降低有利于减小增程器的体积和质量(称之为增程器的小型化),进而降低成本、节省安装空间.

增程器小型化必然对E-REV的能量管理策略提出更高的要求,文中针对一款E-REV,基于搭建的整车动力系统和控制策略仿真模型,首先对增程器小型化的方法进行研究;其次采用逐步优化的方法提出4种E-REV规则型控制策略;然后分别从发动机工作点分布、增程器效率以及动力电池充放电能量损失等方面对比分析各策略燃油经济性存在差异的原因;最后,利用dSPACE设备进行硬件在环仿真试验,以验证提出的E-REV能量管理策略在实时状态下的控制效果,为其工程应用提供参考和理论指导.

1 增程器小型化的方法

E-REV的设计指标要求增程模式时车辆能够在FTP-72城市工况、NEDC城市/市郊工况以及HWFET高速工况下行驶,并且能以100 km·h-1的巡航车速行驶.根据E-REV工作模式和动力系统的特点[12],要求增程模式时动力电池的荷电状态(state of charge,SOC)保持平衡.因此,所匹配的发动机其最大功率应至少能满足所有设计工况的持续功率需求.

针对同一整车配置参数而循环工况不同的情况,通过仿真计算可知,上述4种工况下对发动机的功率需求分别为6,7,14,20 kW,因此,发动机的最大功率应大于20 kW.图1为所选25 kW发动机的等效率曲线,M点为其高效点,N点为次高功率点,对应的输出功率分别为12,20 kW.

图1 25 kW发动机等效率曲线

2 E-REV规则型能量管理策略

2.1 发动机开/关能量管理策略

发动机开/关控制策略要求增程模式时电池SOC在下限值SOCl和上限值SOCh之间变化,且要求发动机输出定值功率Pice_cons.

由于车辆实际行驶工况的不确定性,Pice_cons的选取须满足所有设计工况的功率需求,同时为了提高车辆的燃油经济性,应尽量使发动机工作在高效点.适当加大[SOCl,SOCh]的范围有利于减少动力电池的充放电次数,但范围过大不利于动力电池外接充电时充入尽可能多的电能,导致车辆使用成本增加.

2.2 功率跟随能量管理策略

增程模式下采用功率跟随控制策略时,为了维持动力电池SOC的平衡,须根据SOC附加一定的功率,该附加功率为

(1)

式中kchar为充电功率系数.

根据动力母线上的整车需求功率PT、发电机效率ηgen以及附加功率Padd,计算得到发动机需求功率为

Pice_req=PT/ηgen+Padd.

(2)

由式(2)可知,E-REV采用功率跟随控制策略时,发动机功率将在一个较大的范围内变化,为了提高效率,要求发动机工作点沿最优曲线移动.

2.3 最优曲线能量管理策略

由于增程器的小型化,使得E-REV采用发动机开/关控制策略时,发动机需工作在图1中的N点.根据图2发动机工作点效率与输出功率的关系曲线可知,N点的燃油效率远小于M点,因此必然造成E-REV低速工况下燃油经济性的下降.

图2 发动机工作点效率曲线

如图1所示,可将发动机的最优曲线划分为4个区间,即低功率RL(P～Q线段)、中低功率RML(Q～M线段)、中高功率RMH(M～N线段)和高功率区间RH.其中,u,v,w分别为RL,RML和RMH区间内的任一点,对应的发动机功率分别为Pu,Pv和Pw,分界点P,Q,M,N对应的发动机输出功率分别为PP,PQ,PM和PN.同理,可将电池SOC划分为高、中、低3个区间,即[SOCh,SOCdisc]、[SOCdisc,SOCchar]和[SOCchar,SOCl].其中,SOCdisc和SOCchar分别为动力电池的放电和充电阈值,即当SOC大于SOCdisc时,使动力电池放电,当SOC小于SOCchar时,给动力电池充电.

基于上述发动机最优曲线和动力电池SOC的区间划分情况,如果某一时刻的整车需求功率较低,例如为Pu时,若此时SOC处于低区间内,为了维持SOC的平衡,发动机应输出较大的功率以满足车辆行驶和电池充电的功率需求,因此发动机的目标功率应取PM;相反,若SOC处于高区间内,则发动机的目标功率应取0,以便于动力电池放电.依此方法可建立增程模式时E-REV最优曲线策略的控制规则,如表1所示.

表1 E-REV最优曲线策略的控制规则

2.4 功率分流能量管理策略

由于发动机开/关控制策略在电池放电阶段的电能消耗全部来自充电阶段所充入的电能,多重的能量转换导致燃油经济性的下降.采用功率分流控制策略可对电池充、放电阶段的发动机工作点进行优化.

图3给出了功率分流策略的控制规则.在电池充电阶段,仅在整车需求功率小于PM时,才进入行车充电模式,且在该模式下发动机工作在最高效率点.在放电阶段,仅在整车需求功率小于PP时,才进入仅有电池驱动的模式.与发动机开/关控制策略相比,功率分流控制策略中电池充、放电过程的持续时间更长,能够有效减少电池充、放电循环的次数以及内阻上的能量损失.

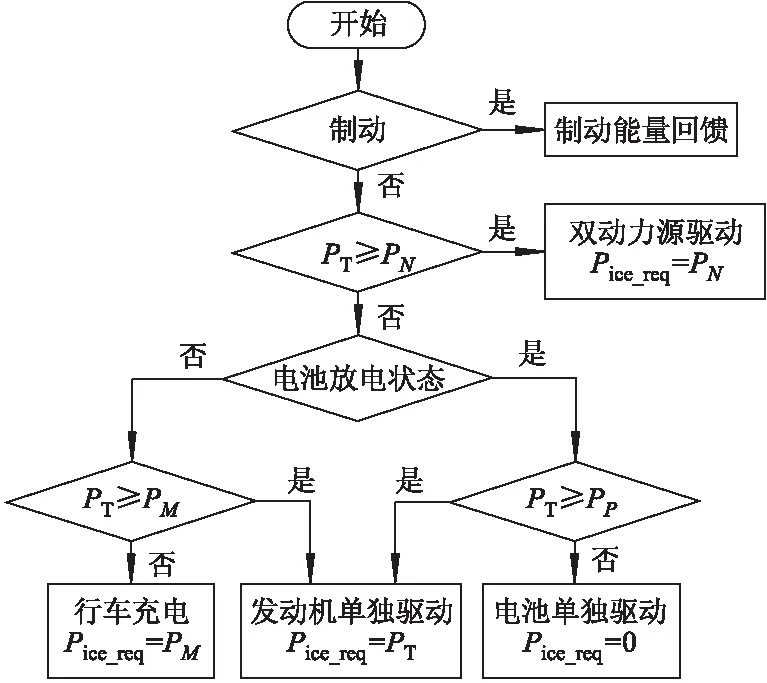
图3 功率分流策略的控制规则流程图

3 仿真结果对比分析

为了对比上述4种控制策略的优劣,可将Simulink环境下搭建的控制策略模型生成动态链接库文件,然后嵌入到Cruise环境下的E-REV整车模型中进行仿真计算.

3.1 仿真结果

3.1.1 发动机开/关控制及功率跟随控制策略

图4为采用发动机开/关控制策略时,10个NEDC工况下,电池SOC随车速的变化情况.其中,发动机输出功率取20 kW.从图4可以看出:电池SOC在25%至35%范围内有规律地波动,电池具有明显的充电和放电过程.

图5为采用功率跟随控制策略时,单个NEDC工况下,电池SOC和发动机功率的仿真结果.从图5可以看出:电池SOC能较好地控制在目标值30%附近,且曲线变化比较平滑,没有明显的充、放电循环过程.发动机工作点多分布在燃油效率较低的区域.

图4 发动机开/关控制策略的仿真结果

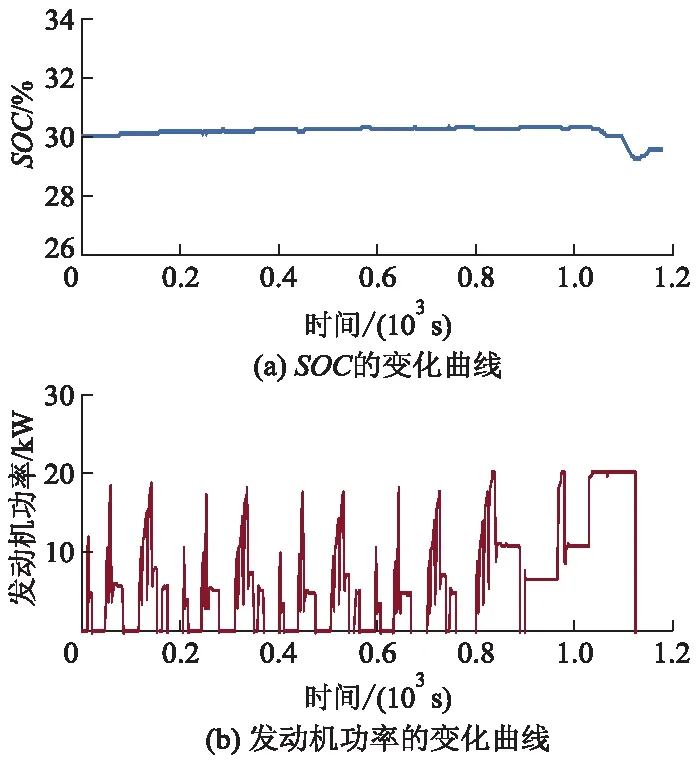
图5 功率跟随控制策略的仿真结果

3.1.2 最优曲线控制策略

图6为采用最优曲线控制策略时,单个NEDC工况下,电池SOC和发动机功率的仿真结果.可以看出,电池SOC曲线比较平滑,且维持在指定的范围内.与图5相比,图6中发动机运行在高效点的时间更长,有利于提高E-REV在增程模式下的燃油经济性.

图6 最优曲线控制策略的仿真结果

3.1.3 功率分流控制策略

图7为采用功率分流控制策略时,10个NEDC工况下,电池SOC和工况车速的仿真结果.

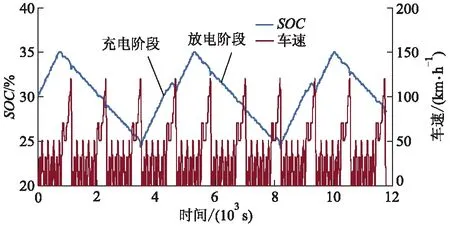
图7 功率分流控制策略的仿真结果

从图7可以看出:增程模式下当采用功率分流控制策略时,电池具有明显的充、放电循环,且电池SOC能被有效地控制在指定的区间范围内,与图4发动机开/关控制策略相比,电池的充、放电循环次数约减少了70%.

3.2 对比分析

采用等效燃油消耗折算方法对各策略的燃油经济性进行仿真计算,不同策略和工况下的仿真结果如表2所示,最优曲线策略和功率分流策略具有较好的燃油经济性,发动机开/关策略的燃油经济性较差.下面从发动机工作点分布、增程器效率以及动力电池充放电能量损失等方面分析燃油经济性存在差异的原因.

表2 不同策略下的燃油经济性对比 L·(100 km)-1

1) 发动机工作点分布.SOC初始值取30%,图8为单个NEDC工况下,4种策略所对应的发动机工作点沿最优曲线的分布情况.

由图8a可以看出:除了加载过程中所产生的个别过渡点之外,发动机总是工作在次高功率点.从图8b可以看出,发动机工作点覆盖了最优曲线的低、中、高功率段.与图8b相比,图8c中落在中、低功率段的工作点大幅较少,发动机工作点集中分布在高效点.图8d中,发动机工作点在高效点的分布情况与图8c相似,在中、低功率段的分布介于图8b和图8c之间.

图8 发动机工作点分布

2) 增程器平均发电效率.E-REV动力系统结构中,发动机驱动发电机以输出电能的方式向动力母线供电,根据发动机和发电机工作点的效率可计算增程器的平均效率，即

(3)

式中:ηRE_ave为增程器的平均效率,%;ηice(i)和ηgen(i)分别为发动机和发电机第i个工作点的效率,Cruise软件中效率的采样周期设置为0.5 s；n为工作点总数.

根据发动机工作点效率可计算其平均效率,即

(4)

式中ηice_ave为发动机平均效率,%,发电机平均效率的计算与发动机类似.

单个NEDC工况下,上述4种控制策略所对应的发动机、发电机和增程器平均效率见表3.

表3 增程器平均效率对比 %

从表3可以看出:增程器的平均效率取决于发动机和发电机,是其综合作用的结果,并且当采用不同的控制策略时,增程器的平均效率与E-REV增程模式下的燃油经济性相对应(见表2).

3) 电池充、放电能量损失.增程模式下,动力电池起到负荷调节装置的作用,电池充、放电过程中必然存在内阻上能量的损失.指定工况下,电池的充、放电能量及其能量损失的计算如下:

(5)

(6)

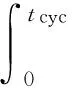
(7)

式中:Wchar_batt,Wdischar_batt和Wloss_batt分别为电池充电能量、放电能量和内阻能量损失,kJ;Pchar_batt,Pdischar_batt和Ploss_batt分别为电池充电功率、放电功率和内阻损失功率,kW;tcyc为工况时间,s.

单个NEDC工况下分别采用上述4种控制策略时,电池充电能量、放电能量以及充放电能量损失的仿真结果分别如图9-11所示.

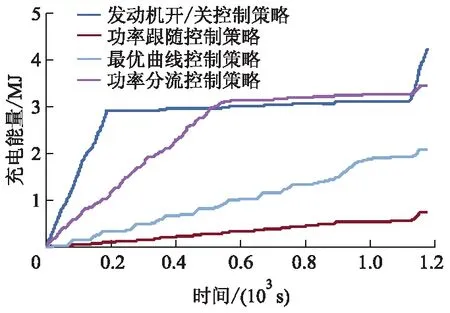
图9 电池充电能量的仿真结果

图10 电池放电能量的仿真结果

图11 电池充放电过程中能量损失的仿真结果

从图9-11可以看出:采用发动机开/关控制策略时,动力电池具有最大的充、放电能量及能量损失,原因在于发动机工作在次高功率点,且动力电池具有完整的充放电过程(见图4).与其他控制策略相比,功率跟随控制策略下电池的充、放电能量及其能量损失最小,但由于该策略下增程器的平均效率较低(见表3),因此并不具有最好的燃油经济性.与功率分流控制策略相比,最优曲线控制策略下电池的充放电能量损失更少,同时该策略具有最高的增程器平均效率,因此最优曲线控制策略具有最好的燃油经济性.

4 硬件在环仿真试验验证

为了验证各策略的控制效果,设计开发了整车控制器(vehicle control unit,VCU),使用dSPACE公司的软硬件设备完成了控制策略模型转换和Targetlink自动代码生成,并将生成的代码下载到VCU中.搭建的硬件在环仿真试验平台如图12所示.

针对每一种策略,根据电池SOC初值的不同分以下2种情况进行仿真试验: ①SOC初值取35%,便于验证电池放电以及SOC平衡的控制效果; ②SOC初值取25%,便于同时考查策略对电池充电过程和SOC平衡过程的综合控制效果.为了便于试验结果的对比,所采用的整车配置参数与之前离线仿真模型的参数相同.图13，14分别给出了上述2种情况下,选取NEDC工况时E-REV最优曲线控制策略的硬件在环仿真试验结果.

图12 硬件在环仿真试验平台搭建

图13 仿真试验结果(SOC初值取35%)

从图13可以看出:在试验初始阶段,E-REV处于纯电动模式,当SOC下降到30%时,进入增程模式,发动机和电池共同驱动车辆行驶,电池SOC维持在30%附近,控制效果良好.

图14 仿真试验结果(SOC初值取25%)

由图14可以看出:车辆起动后直接进入增程模式,电池SOC曲线呈逐渐上升的趋势.原因在于增程模式下SOC的控制目标值为30%,当SOC初值取25%时,策略的控制作用必然使SOC首先趋向于目标值,然后才能进入SOC的平衡阶段.通过图13和图14的对比可以看出:当电池SOC取不同的初始值时,电池功率曲线之间差异较大,如图14中在SOC的上升阶段,电池大部分时间处于充电状态(规定电池功率为正表示充电,为负表示放电),而图13中则正好相反.从图13，14的发动机功率曲线可以看出，中、低速工况下,发动机能较好地集中在高效点工作.

FTP-72和HWFET工况下的硬件在环仿真试验结果与NEDC工况类似,不再赘述.

5 结 论

1) 配置了小型化增程器的E-REV,不适合采用发动机开/关和功率跟随控制策略,当采用功率分流和最优曲线控制策略时,E-REV具有较好的燃油经济性和控制效果.

2) 增程器平均效率和动力电池充放电能量损失是影响E-REV燃油经济性的主要因素,为了提高E-REV的燃油经济性,应控制发动机运行在最优曲线上,且尽可能多地工作在高效点.

参考文献(References)

[ 1 ] GUANETTI J, FORMENTIN S, SAVARESI S M. Energy management system for an electric vehicle with a rental range extender: a least costly approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(11): 3022-3034.

[ 2 ] 王耀楠,孟步敏,申永鹏,等.燃油增程式电动汽车动力系统关键技术综述[J].中国电机工程学报,2014, 34(27):4629-4639.

WANG Y N, MENG B M, SHEN Y P, et al. Researches on power systems of extended range electric vehicles[J]. Proceedings of the Chinese Society for Electrical Engineering, 2014, 34(27): 4629-4639. (in Chinese)

[ 4 ] 徐成善,江发潮,宋森楠,等.增程式电动客车能量管理策略优化的研究[J].汽车工程,2017,39(1): 9-14.

XU C S, JIANG F C, SONG S N, et al. A study on ener-gy management strategy optimization for extented-range electric bus[J]. Automotive Engineering, 2017,39(1):9-14. (in Chinese)

[ 5 ] 牛继高,司璐璐,周苏,等.增程式电动汽车能量控制策略的仿真分析[J].上海交通大学学报,2014,48(1):140-145.

NIU J G, SI L L, ZHOU S,et al. Simulation analysis of energy control strategy for an extended-range electric vehicle[J]. Journal of Shanghai Jiaotong University,2014,48(1):140-145. (in Chinese)

[ 6 ] 宋桂秋,王凯,李一鸣.增程式电动汽车多模式切换控制策略与性能仿真[J].科学技术与工程,2016,16(31):94-100.

SONG G Q, WANG K, LI Y M. Multi-mode switching control strategy and performance simulation study of extended-range electric vehicle[J]. Science Technology and Engineering, 2016,16(31): 94-100. (in Chinese)

[ 7 ] JIANG Y C, LIN C, CAO W K. Parameters optimization for extended-range electric vehicle based on improved chaotic particle swarm optimization[J]. International Journal of Grid and Distributed Computing, 2016, 9(9): 1-10.

[ 8 ] 申永鹏,王耀南,孟步敏,等.增程式电动汽车增程器转速切换/功率跟随协调控制[J].中国机械工程,2015,26(12):1690-1696.

SHEN Y P, WANG Y N, MENG B M, et al. Cooperative control strategy of power following-speed switching in a range extender electric vehicle APU[J]. China Mechanical Engineering, 2015, 26(12): 1690-1696. (in Chinese)

[ 9 ] LIU D Q, WANG Y N, ZHOU X, et al. Extended range electric vehicle control strategy design and muti-objective optimization by genetic algorithm[C]∥2013 Chinese Automation Congress. USA:IEEE,2013: 11-16.

[10] FERNANDEZ R A, CILLERUELO F B, MARTINEZ I V. A new approach to battery powered electric vehicles: a hydrogen fuel-cell-based range extender system[J]. International Journal of Hydrogen Energy, 2016, 41(8):4808-4819.

[11] HWANG J J, HU J S, LIN C H. Design of a range extension strategy for power decentralized fuel cell/battery electric vehicles[J]. International Journal of Hydrogen Energy, 2015, 40(35): 11704-11712.

[12] CIPEK M, SKUGOR B, CORIC M, et al. Control varia-ble optimisation for an extended range electric vehicle[J]. International Journal of Powertrains, 2016, 5(1): 30-54.