智能汽车驾驶员模型的预瞄时间自适应分析

解 炬, 江浩斌, 马世典

(江苏大学 汽车与交通工程学院, 江苏 镇江 212013)

近年来,计算机、互联网等高新技术的迅速发展有力地促进了汽车智能化技术研发和应用.驾驶员模型是智能车辆和汽车辅助驾驶技术研究的关键之一,同时在人-车-路闭环系统研究中也具有重要作用[1].20世纪50年代国外研究人员首次提出驾驶员模型概念,主要针对方向控制驾驶员模型进行研究.根据模型中是否存在驾驶员预瞄过程,将驾驶员模型分为补偿跟踪模型和预瞄跟踪模型.20世纪90年代形成了基于模糊控制理论和人工神经网络等算法的智能控制驾驶员模型,该类模型的出现奠定了智能汽车驾驶员模型的研究基础[2].

对于智能汽车而言,驾驶员操纵汽车的行为可视为一个不断反复进行的“信息感知—轨迹决策—操作校正”的过程[3].驾驶员的行为受到汽车特性、道路环境以及自身因素的影响,因此,应全面分析研究驾驶员的行为特性,以便建立准确的智能汽车驾驶员模型.

智能汽车驾驶员模型中的预瞄过程属于“信息感知”环节中的前视行为.在以往的驾驶员模型中,普遍采用固定的预瞄时间,但在实际驾驶过程中,预瞄时间往往受到各种因素的影响.文献[4]分析了驾驶员前视行为的主要影响因素.文献[5]根据道路曲率对预瞄时间进行了修正.文献[6]设计了模糊控制器对预瞄距离进行模糊选择.文献[7]根据4种优化指标选取最优预瞄时间.

文中基于预瞄跟随理论构建智能汽车驾驶员模型,进而分析道路环境与汽车行驶状态等因素对智能汽车驾驶员模型中预瞄时间的影响,分别采用基本预瞄时间和补偿预瞄时间表征不同因素对驾驶员前视行为的影响,并将基本预瞄时间和补偿预瞄时间相结合,建立基于BP神经网络的预瞄时间自适应模型,最后通过仿真试验证明该预瞄时间自适应模型的有效性.

1 智能汽车驾驶员模型

1.1 预瞄机理

在车辆的实际行驶过程中,驾驶员通常以车辆的当前运动状态为基础,预测车辆行驶至前方预瞄点时车辆与期望跟踪道路轨迹之间的侧向偏差,该偏差即为侧向预瞄偏差.驾驶员调整转向盘的目的就是为了使该侧向预瞄偏差尽可能为0.如图1所示,图中定义了期望路径的地面坐标系(OXY)与固定于移动车辆上的车辆坐标系(oxy),L为预瞄距离,Δfp即为车辆坐标系下侧向预瞄偏差.

图1 驾驶员预瞄机理示意图

驾驶员在实际驾驶过程中会根据侧向预瞄偏差的正负和大小来转动转向盘调节前轮转角,实现对车辆实际行驶路径的调节.

1.2 预瞄跟随理论

为了对驾驶员的路径跟踪行为进行建模,采用了预瞄跟随理论.预瞄跟随理论描述一个可以预测未来输入的跟随系统,可定义为由“预瞄器”与“跟随器”相串联.预瞄跟随理论结构简图如图2所示,P(s)为驾驶员预瞄过程的预瞄函数,F(s)为包括驾驶员行为和车辆响应的跟随函数,f为道路轨迹输入,fe为有效的预瞄输入,y为车辆的侧向位移.由于通常驾驶情况下驾驶员的操作是低频过程,预瞄跟随系统应在低频域内满足P(s)·F(s) ≈ 1,以获得一个理想的跟随效果[8].

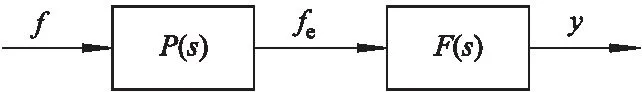
图2 预瞄跟随理论结构简图

1.3 预瞄优化神经网络驾驶员模型

通常情况下,一个合格驾驶员的驾驶行为与预瞄跟随理论相契合[9].因此在预瞄跟随理论的基础上,建立如图3所示的简化预瞄优化神经网络驾驶员模型(POSANN).在预瞄器P(s)中,驾驶员可以通过预瞄过程从目标道路轨迹f获取有效道路预瞄信息fe,其传递函数为etps,tp为驾驶员路径跟踪预瞄时间.

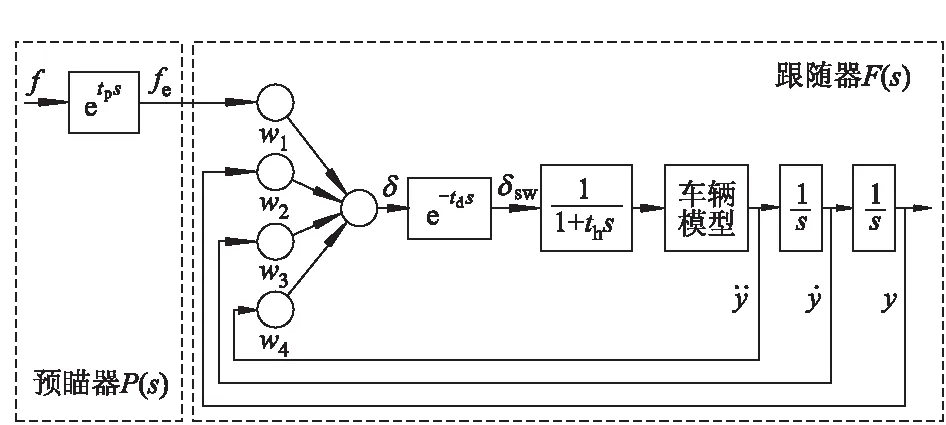
图3 简化的预瞄优化神经网络驾驶员模型

1.4 智能汽车驾驶员模型

在智能汽车的研究中,智能汽车驾驶系统实质上是一种可以替代驾驶员来控制车辆的智能控制系统[8],图4为该系统的结构示意图.

图4 智能汽车控制系统结构示意图

智能汽车控制系统包括信息感知子系统、轨迹决策子系统和操纵控制子系统3部分.其中,感知子系统相当于向预瞄器提供前方道路信息;决策子系统反映驾驶员的行驶轨迹决策策略,相当于实现预瞄器的功能;操纵子系统根据驾驶员的轨迹决策信息产生操作动作,相当于跟随器的功能.

可见, 智能汽车控制系统的3个子系统分别对应着预瞄跟随理论中的3个环节,体现了驾驶员的控制行为特性.因此,可以根据预瞄跟随理论,并结合图3所示的预瞄优化神经网络驾驶员模型,来构建图4所示的智能汽车驾驶员模型,从而对智能汽车驾驶系统进行深入研究.

2 预瞄时间自适应

在真实驾驶员操作过程中,驾驶员的前视行为会受到汽车行驶状态、道路环境和驾驶员个人驾驶风格等因素的影响.同样,在智能汽车驾驶员模型中,驾驶员的预瞄时间对“驾驶员-汽车-道路”闭环系统的影响非常显著,固定预瞄时间的驾驶员模型难以适应智能汽车复杂的行驶状况.因此,从驾驶员的驾车实际情况出发,选取影响驾驶操作的主要因素进行分析,分别采用基本预瞄时间和补偿预瞄时间表征不同因素对驾驶员前视行为的影响,并将基本预瞄时间和补偿预瞄时间相结合,以构建预瞄时间自适应模型.

2.1 基本预瞄时间

图5 基本预瞄时间规则库

由图5可以看出:基本预瞄时间随车速增大而明显增大,随路面附着系数减小而减小.车速在10～100 km·h-1时,基本预瞄时间为0.5～2.0 s.

2.2 补偿预瞄时间

在智能汽车驾驶员模型中,道路环境与汽车行驶状态等因素对驾驶员前视行为的影响采用补偿预瞄时间进行表征.通过分析不同预瞄时间下的路径跟踪误差来构建理想补偿预瞄时间,并选取影响预瞄时间的4种因素进行相关性分析.

2.2.1 理想补偿预瞄时间

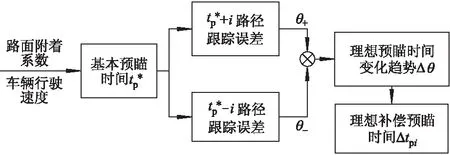
图6 理想补偿预瞄时间Δtpi计算过程

2.2.2 补偿预瞄时间影响因素相关性分析

经过反复仿真试验,选取了预瞄轨迹偏差λ、道路曲率ρ、横摆角速度ω、路径跟踪误差θ等4种影响预瞄时间的因素进行不同车速v和道路附着系数μ下与理想补偿预瞄时间Δtpi的相关性分析.各因素相关系数绝对值如图7所示,图7直观地显示了各影响因素与理想补偿预瞄时间的相关程度.

图7 补偿预瞄时间与影响因素的相关程度

从图7可以看出:补偿预瞄时间与λ,ρ,ω这3种影响因素之间具有较强的相关性,而与θ之间具有较弱的相关性.因此,λ,ρ,ω是影响补偿预瞄时间的主要因素,θ是影响补偿预瞄时间的次要因素.结合以上4种影响因素以及v和μ,利用智能控制算法对补偿预瞄时间进行优化,实现智能汽车驾驶员模型预瞄时间自适应调整.

2.3 预瞄时间自适应模型

2.3.1BP神经网络原理

BP(back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,具有强大的学习和适应能力.BP神经网络的学习过程如图8所示,该学习过程主要由信息的正向传播与误差的逆向传播2个过程组成.

图8 BP神经网络算法流程图

2.3.2 网络拓扑结构的确定

BP神经网络拓扑结构方案使用1个输入层,6个输入结点(λ,ρ,ω,θ,v,μ)与1个输出层,1个输出结点(理想补偿预瞄时间Δtpi).

采用式(1)确定网络隐含层节点数范围,并通过试凑法,根据公式范围内不同节点数下网络误差的变化趋势确定最合理的节点数.

(1)

式中:m为输入层节点数;n为输出层节点数;b为0～10之间的常数.

2.3.3 网络训练结果

神经网络训练结果如图9所示.

图9 神经网络训练结果

从图9可以看出,神经网络训练出的补偿预瞄时间Δtp能够很好符合理想补偿预瞄时间Δtpi.

图10 预瞄时间自适应模型框图

3 模型验证

3.1 仿真模型

为验证上述预瞄时间自适应模型的有效性,在Carsim/Simulink联合仿真平台中搭建了预瞄时间自适应的智能汽车驾驶员模型并进行了仿真研究.Carsim仿真车辆采用B级轿车.仿真中所使用的道路模型采用Alt 3 from FHWA,其跟踪路径如图11所示,路径总长度为1 km.

图11 车辆跟踪路径

3.2 仿真结果

为了验证预瞄时间自适应模型的有效性,针对正常驾驶和激进驾驶2种驾驶模式进行仿真.

正常驾驶模式下,纵向加速度a1控制方程为

(2)

式中:kpn,kin,kpn3为增益系数,kpn=0.4,kin=0.1,kpn3=4;verr为速度跟踪误差;t为时间.

在a1≤3 m·s-2,v≤ 80 km·h-1时,正常驾驶模式下速度与加速度变化曲线如图12所示.正常驾

驶模式下,分别采用基本预瞄时间和自适应预瞄时间进行路径跟踪仿真结果对比如图13所示.

从图13a可以看出:在正常驾驶模式下,自适应预瞄时间下智能汽车驾驶员模型相较于基本预瞄时间下智能汽车驾驶员模型具有较小的路径跟踪误差.从图13b可以看出:在正常驾驶模式下,自适应预瞄时间下智能汽车驾驶员模型能有效减少累积跟踪误差.

激进驾驶模式下,纵向加速度a2控制方程为

(3)

式中：kpa,kia,kpa3为增益系数,kpa=0.4,kia=0,kpa3=2；t为时间.

在a2≤7 m·s-2,v≤150 km·h-1时,激进驾驶模式下速度与加速度变化曲线如图14所示.

图13 正常驾驶模式下模型仿真结果

图14 激进驾驶模式下速度与加速度变化曲线

激进驾驶模式下,分别采用基本预瞄时间和自适应预瞄时间进行路径跟踪仿真，结果对比如图15所示.从图15a可以看出:在激进驾驶模式下,自适应预瞄时间下智能汽车驾驶员模型能有效减少路径跟踪误差.从图15b可以看出:在激进驾驶模式下,自适应预瞄时间下智能汽车驾驶员模型能有效减少累积跟踪误差.如图13c,15c所示,基本预瞄时间主要受车速的影响,而自适应预瞄时间受到道路环境与汽车行驶状态等因素的综合影响,能更好地反映驾驶员的实际驾驶特征.因此,自适应预瞄时间下智能汽车驾驶员模型具有更好路径跟踪效果.

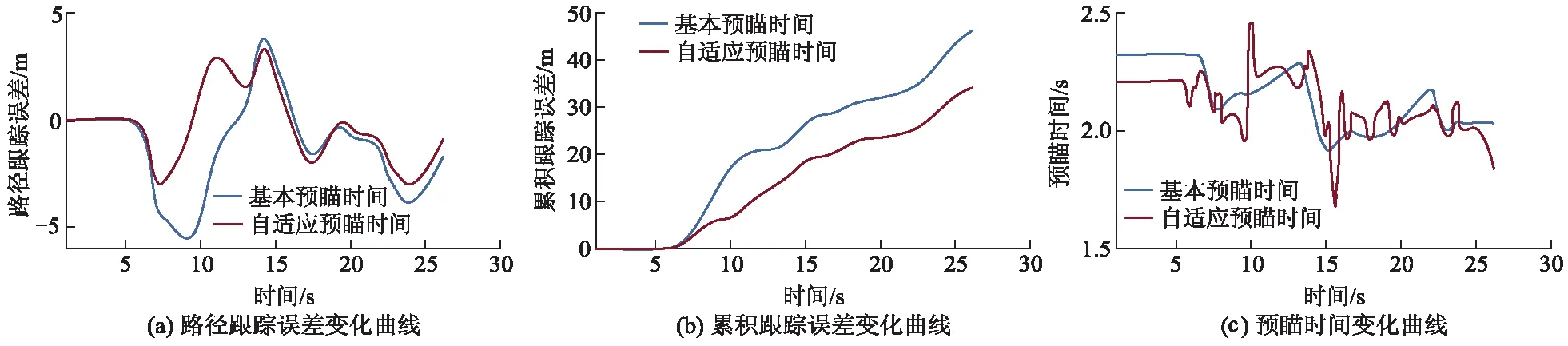
图15 激进驾驶模式下模型仿真结果

4 结 论

基于预瞄跟随理论与预瞄优化驾驶员模型构建了智能汽车驾驶员模型.从道路环境与汽车行驶状态等因素中选取了影响预瞄时间的主要因素进行分析,分别采用基本预瞄时间和补偿预瞄时间表征不同因素对驾驶员前视行为的影响,并将基本预瞄时间和补偿预瞄时间相结合,建立了基于BP神经网络的预瞄时间自适应模型.自适应预瞄时间受多种驾驶因素的综合影响,能更好地反映驾驶员的实际驾驶特征.仿真试验结果表明:该预瞄时间自适应模型能够有效减少智能汽车驾驶员模型在正常驾驶模式下的累积跟踪误差,并能够有效减少智能汽车驾驶员模型在激进驾驶模式下的路径跟踪误差与累积跟踪误差.

参考文献(References)

[ 1 ] 陈涛, 李晓旭, 孙林, 等. 智能车辆设计中驾驶员模型回顾与展望[J]. 汽车技术, 2014(6): 1-6.

CHEN T, LI X X, SUN L, et al. Review and outlook of the driver model in intelligent vehicle design[J]. Automobile Technology, 2014(6): 1-6. (in Chinese)

[ 2 ] 郭景华, 李克强, 罗禹贡. 智能车辆运动控制研究综述[J]. 汽车安全与节能学报, 2016, 7(2): 151-159.

GUO J H, LI K Q, LUO Y G. Review on the research of motion control for intelligent vehicles[J]. Journal of Automotive Safety and Energy, 2016, 7(2): 151-159. (in Chinese)

[ 3 ] 高振海, 管欣, 郭孔辉. 驾驶员方向控制模型及在汽车智能驾驶研究中的应用[J]. 中国公路学报, 2000, 13(3): 106-109.

GAO Z H, GUAN X, GUO K H. Driver directional control model and the application in the research of intelligent vehicle[J]. China Journal of Highway and Transport, 2000, 13(3): 106-109. (in Chinese)

[ 4 ] 王兵. 驾驶员对汽车方向的自适应控制行为建模研究[D]. 长春:吉林大学, 2009.

[ 5 ] 李英. 方向与速度综合控制驾驶员模型及在ADAMS中的应用[D]. 长春:吉林大学, 2008.

[ 6 ] 陈无畏, 王家恩, 汪明磊,等. 视觉导航智能车辆横向运动的自适应预瞄控制[J]. 中国机械工程, 2014, 25(5):698-704.

CHEN W W, WANG J E, WANG M L, et al. Adaptive preview control of vision guided intelligent vehicle lateral movement[J]. China Mechanical Engineering, 2014, 25(5):698-704. (in Chinese)

[ 7 ] 李红志, 李亮, 宋健,等. 预瞄时间自适应的最优预瞄驾驶员模型[J]. 机械工程学报, 2010, 46(20): 106-111.

LI H Z, LI L, SONG J,et al. Optimal preview control driver model with adaptive preview time[J]. Journal of Mechanical Engineering, 2010, 46(20): 106-111. (in Chinese)

[ 8 ] 高振海, 管欣, 郭孔辉. 预瞄跟随理论和驾驶员模型在汽车智能驾驶研究中的应用[J]. 交通运输工程学报, 2002, 2(2): 62-66.

GAO Z H, GUAN X, GUO K H. Application of preview follower theory and driver model in the research of vehicle intelligent handling[J]. Journal of Traffic and Transportation Engineering, 2002, 2(2): 62-66. (in Chinese)

[ 9 ] CAO J Y, LU H, GUO K H, et al. A driver modeling based on the preview-follower theory and the jerky dynamics[J]. Mathematical Problems in Engineering, 2013(1): 1-10.

[10] DING H T, GUO K H, WAN F, et al. An analytical driver model for arbitrary path following at varying vehicle speed[J]. International Journal of Vehicle Autonomous Systems, 2007, 5(3/4): 204-218.