压水堆燃料棒热力计算与(火用)分析

张钧波, 张功伟, 张 敏

(1. 南京师范大学 泰州学院, 江苏 泰州 225300; 2. 南京理工大学 能源与动力工程学院, 江苏 南京 210094)

核反应堆的安全运行是近代核科学研究的重要课题,在保证堆芯释热有效输出的前提下,尽可能提高核能利用率,也是核动力装置热工设计的主要研究方向[1-3].堆芯内燃料棒传热主要包括芯块导热、包壳传热以及包壳外壁面与冷却剂对流换热3部分,目前研究方法大多以热力学第一定律为基础[4-6],通过数值计算方法对燃料组件传热通道进行模拟计算,从而获得燃料棒及外围冷却剂的温度分布或者包壳表面的热流密度[7-10].但对于燃料棒内能量在数量和质量上综合性研究较少,因此不能准确全面地反映用能过程中存在的薄弱环节.

文中结合热力学第一、第二定律,在系统能量平衡的基础上,先采用数值法和解析法获得燃料棒温度场,验证模型的准确性,然后通过(火用)分析法计算正常工况下燃料棒传热过程中(火用)损的分布情况,为节能降耗、提高能量利用率提供参考.

1 模型验证

在压水堆中燃料棒长度L一般为3～4 m,外径为9.5 mm左右,按设计要求将一定数量燃料芯块装入包壳内,燃料棒外围为热通道,冷却剂自下而上流动,进行对流换热.燃料棒轴向截面如图1所示,Ru为芯块半径,Rci为包壳内径,Rcs为包壳外径.

图1 燃料棒轴向截面图

1.1 控制方程和离散方程

对于通用物理变量φ,一般的稳态扩散方程为

(1)

式中:f(xi)为几何形状因子；Γφ为对应变量φ的扩散系数;Sφ为单位体积中的净源项.

根据方程(1),在圆柱坐标系中,燃料棒的稳态导热微分方程为

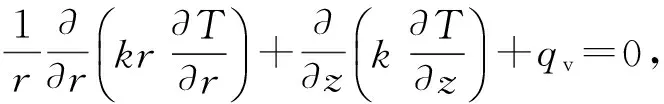
(2)

式中:r为圆柱坐标系半径;k为导热系数;∂T/∂r为r方向的温度变化率;∂T/∂z为z方向的温度变化率;qv为热源项.

在导热方程中,扩散系数Γ即为热传导系数k,反应堆正常运行工况下的热源项近似为

(3)

式中J0为第一类贝赛尔函数.

计算时采用非结构化网格,对方程(1)进行离散.在一个控制体P中,有

(4)

式中:n为控制体P与其他控制体的交界面数;VP为控制体P体积;SP为控制体P的净源项;Di为扩散项,可表示为交界面i上的法向扩散项Dpi和切向扩散项Dsi之和.

(5)

(6)

式中:φE和φP分别为控制体E和控制体P的通用物理变量;dsi为两控制体的中心距;esi为其中心连线的单位矢量.

(7)

将式(7)代入式(6),然后根据式(5),有

(8)

(9)

于是完整的离散方程可写成:

(10)

(11)

该离散方程是基于方程(1)推导的,与坐标无关,适用于任何几何形状,具体过程可参阅文献[11].

1.2 边界条件

由于燃料棒的长径比很大,在数值求解时可简化计算模型,以秦山核电二期工程堆芯燃料棒为研究对象,取燃料棒长度L=30 mm,芯块半径Ru=4.1 mm,包壳内径Rci=4.20 mm,包壳外径Rcs=4.75 mm,芯块导热系数ku=3.1 W·(m·K)-1,气隙导热系数kg=0.33 W·(m·K)-1,包壳导热系数kc=17 W·(m·K)-1,冷却剂定压比热容cp=5 800 J·(kg·K)-1,平均线功率密度ql=16.1 kW·m-1,对流换热系数h=40 kJ·(m2·K)-1,热管因子F=2.35,冷却剂入口温度Tin=565 K,冷却剂出口温度Tout=601 K[12].

考虑到燃料棒的周向对称性和轴向延续性,计算时取1/2燃料棒为计算模型,令其上下壁面为定温边界条件,轴向截面为对称边界,包壳壁面为对流换热,数学表达式为

(12)

式中:T1(z)为热通道冷却剂的温度;Tcs为包壳外壁面的温度.

1.3 温度场传热计算

在求解压水堆燃料棒温度场解析解时,做如下假设: ① 轴向释热率呈余弦分布,径向通量展平,即内热源只沿轴向变化; ② 忽略在轴线方向的导热,认为只沿半径方向导热; ③ 忽略冷却剂、燃料或包壳的所有物理变化,即其各物性参数为常数; ④ 冷却剂始终保持为液相,没有相变换热; ⑤ 忽略外推高度的影响[13].

根据上述假设和基本导热微分方程,可求得热通道冷却剂的温度为

(13)

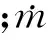
包壳外壁面的温度为

(14)

由于包壳很薄,可以看成无内热源的圆筒壁,则包壳内壁面的温度为

(15)

在包壳与燃料芯块之间有充满氦气的间隙,尽管气隙厚度很小,但由于其导热率很低,会产生相当大的温降,所以必须考虑气隙导热问题.与包壳类似,把气隙看成均匀的圆筒,则芯块表面的温度为

(16)

根据有内热源圆柱体导热问题的求解,芯块中心温度为

(17)

通过式(14)-(17),可以求得燃料棒各点的温度为

(18)

(19)

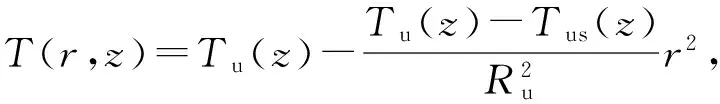
(20)

图2为燃料棒温度分布图,其中实线表示解析解,云图表示数值解,可以看出解析解与数值解得到的温度场吻合良好.

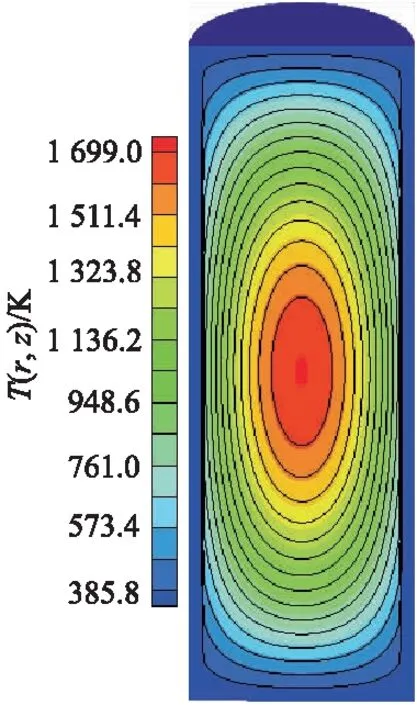
图2 燃料棒温度分布图

图3为不同半径处沿轴向的温度曲线图,从图3可以更清晰看出:在燃料棒包壳区域解析解与数值解基本吻合,越靠近中心误差越大.这是因为解析计算时由外向内,误差逐步叠加,最大达到4.62%,但仍在合理范围内.同时发现,数值模拟时燃料棒是存在轴向传热的,即很小部分热量会向两端传递,也符合实际情况,因此大多数情况下数值解略小于解析解.

图3 不同半径处沿轴向温度曲线图

2 燃料棒的(火用)计算与分析

前面通过求解数值解和解析解得到了燃料棒的温度场分布,并进行对比验证模型的准确性.在此基础上,从能量与质量相结合的角度,通过(火用)分析方法进一步分析燃料棒传热规律以及能量利用率[14].

2.1 核能转化为热能过程

从热力学观点来看,核能都是(火用),若忽略裂变过程中能量的损失,核能(火用)从数值上应等于反应堆热功率Q.对于燃料棒上任一微元体积Vu,其平均温度为Tm,释热量为dqv,假设其处于温度为T0=298.15 K的环境中,理论上其最大热量(火用)为

(21)

根据式(20),燃料芯块任一横截面上0～r范围内平均温度为

(22)

对于整根燃料棒,核能转化为热能过程中(火用)损为

(23)

将式(22)代入式(23),得到燃料棒内核能转化为热能过程中(火用)损为

(24)

2.2 对流换热过程

冷却剂流经燃料棒吸热所得(火用)值为

(25)

对流换热过程的(火用)损为

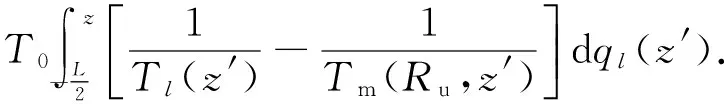
(26)

将式(13)和式(23)代入式(26),即可得冷却剂沿热通道方向的(火用)损分布.

2.3 结果分析

根据式(23),数值求解得到如图4所示燃料棒(火用)损分布图,燃料棒沿轴向两端(火用)损最小,中心处达到最大,整体分布趋势与功率大小相对应.在中心一定区域内,(火用)损增长速率最小,说明此时释热量和温度变化速率基本相等,但随后随着半径增大迅速增加,最大值出现在芯块边缘附近.

图4 燃料棒(火用)损分布图

不同半径和不同横截面处的(火用)损和温度曲线分别如图5，6所示，,核能转换过程的(火用)损主要取决于燃料芯块内温度分布,温度越高,能量形式转换所造成的(火用)损越小.同时可以发现:随着半径的增大,沿轴向(火用)损变化速率随着半径的增大而逐渐增大,在z=0的横截面附近达到最大,而越靠近燃料棒两端,(火用)损变化速率越小.这是由于功率越高,温度波动越剧烈,另一方面,燃料棒由内而外传热热阻不断增大,也将导致系统能量品质下降,做功能力降低,(火用)损变大.

根据式(24),可以得到核能转换为热能过程中总(火用)损分布情况,如图7所示.不同半径处对应的总(火用)损分布曲线如图8所示,总(火用)损从燃料棒底端向上平稳增加,近似呈线性变化,当燃料芯块r=4.10 mm,z=L/2时,该过程总(火用)损约为150 W,(火用)损系数((火用)损与燃料棒总释热量之比)为0.207,而工程实际中由于各种偏差,该系数必然会有所偏大,因此在热工设计时针对性减小(火用)损系数有着重要意义.

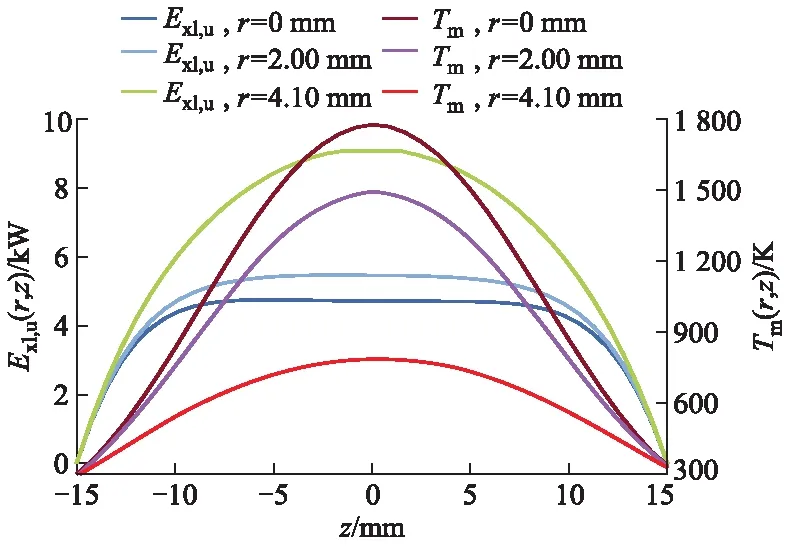
图5 沿轴向的(火用)损和温度变化曲线

图7 燃料棒总(火用)损分布图

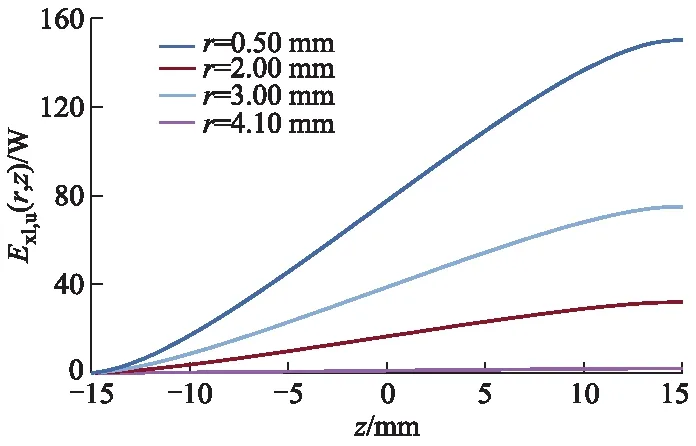
图8 不同半径处总(火用)损变化曲线

根据式(26),可得冷却剂沿热通道方向(火用)损分布,冷却剂沿热通道的(火用)损分布和温度变化曲线如图9所示,(火用)损先增大后减小,而不是与温度一样逐渐增大,这是因为对流换热过程中(火用)损主要取决于燃料芯块与冷却剂之间的传热温差,传热温差越大,(火用)损越大.冷却剂沿热通道的累积(火用)损变化曲线如图10所示,累积(火用)损的变化趋势与温度相似,在热通道中部增长速率较快,在热通道两端增长较慢,该过程累积(火用)损为219 W,相应的(火用)损系数为0.304,两图可相互印证.

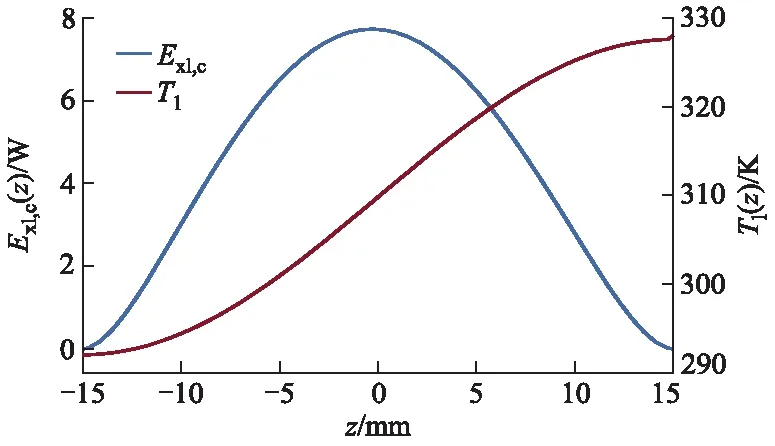
图9 冷却剂沿热通道的(火用)损分布和温度变化曲线

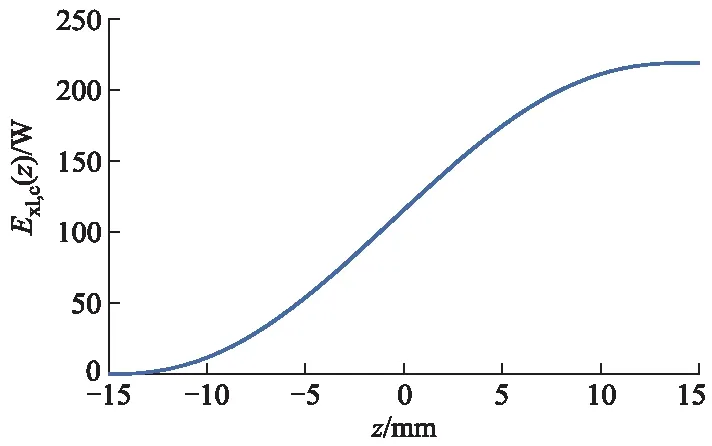
图10 冷却剂沿热通道的累积(火用)损变化曲线

3 结 论

1) 提高能量利用率的本质就是减小(火用)损,燃料棒核能转换为热能过程的(火用)损主要取决于燃料芯块的温度,沿轴向先增大后减小,沿径向不断变大;在燃料芯块边缘处达到最大值,该过程(火用)损系数为0.207.

2) 影响燃料棒与冷却剂对流换热过程(火用)损的主要因素是燃料芯块与冷却剂之间的传热温差,温差越大,(火用)损越大,该过程总(火用)损系数为0.304.

3) 通过温度场和(火用)损分析方法的结合,可以对压水堆堆芯传热过程的优劣程度进行可靠性评估,也能够为优化堆芯稳态热工设计、核燃料装载和冷却剂流量分配方面提供有益参考.

参考文献(References)

[ 1 ] 张蕊,干富军,左巧林,等.压水堆燃料棒束通道内过冷沸腾分析[J].原子能科学技术,2015,49(9):1579-1585.

ZHANG R, GAN F J, ZUO Q L, et al. Analysis of subcooled boiling in PWR rod bundle channel[J].Atomic Energy Science and Technology,2015,49(9):1579-1585.(in Chinese)

[ 2 ] 宋磊,郭赟,曾和义.板状燃料组件入口堵流事故下流场和温度场的瞬态数值计算[J].核动力工程,2014,35(3):6-10.

SONG L, GUO Y, ZENG H Y. Numerical analysis on transient flow and temperature field during inlet flow blockage accidents of plate-type fuel assembly[J]. Nuclear Power Engineering,2014, 35(3):6-10. (in Chinese)

[ 3 ] 卢川,严明宇,毕树茂,等. 基于CFD方法的行波堆19燃料棒束流固耦合传热特性研究[J].原子能科学技术,2015,49(12):2170-2175.

LU C, YAN M Y, BI S M, et al. Study on fluid-solid coupling heat transfer characteristics of TWR assembly with 19 fuel pins based on CFD method[J]. Atomic Energy Science and Technology, 2015, 49(12):2170-2175. (in Chinese)

[ 4 ] 罗磊,陈文振,陈志云,等.单个燃料元件热工水力三维数值模拟[J].海军工程大学学报,2011,23(1):63-66.

LUO L, CHEN W Z, CHEN Z Y, et al. Numerical simulation of thermal hydrodynamic of single reactor fuel rod[J].Journal of Naval University of Engineering,2011,23(1):63-66. (in Chinese)

[ 5 ] SALAMA A, EL-DIN EL-MORSHEDY S. CFD simulation of flow blockage through a coolant channel of atypical material testing reactor core[J]. Annals of Nuclear Energy, 2012, 41: 26-39.

[ 6 ] LI X C, GAO Y. Methods of simulating large scale rod bundle and application to a 17×17 fuel assembly with mixing vane spacer grid[J]. Nuclear Engineering and Design, 2014, 267: 10-22.

[ 7 ] FRICANO J W, BAGLIETTO E. A quantitative CFD benchmark for solidium fast reactor fuel assembly mode-ling[J]. Annals of Nuclear Energy, 2014, 64: 32-42.

[ 8 ] PIRO M H A, LEITCH B W. Conjugate heat transfer simulations of advanced research reactor fuel[J]. Nuclear Engineering and Design, 2014, 274: 30-43.

[ 9 ] RASU N G, VELUSAMY K, SUNDARARAJAN T, et al. Simultaneous development of flow and temperature fields in wire-wrapped fuel pin bundles of sodium cooled fast reactor[J]. Nuclear Engineering and Design, 2014, 267: 44-60.

[10] LIU C C, FERNG Y M, SHIH C K. CFD evaluation of turbulence models for flow simulation of the fuel rod bundle with a spacer assembly[J]. Applied Thermal Engineering, 2012, 40: 389-396.

[11] ZHANG M. Modeling of radiative heat transfer and diffusion processes using unstructured grid[D]. Cookeville: Tennessee Technological University, 2000.

[12] 闵元佑,黄云.秦山核电二期工程反应堆及反应堆冷却剂系统设计[J].核动力工程, 2003,24(2):1-7.

MIN Y Y, HUANG Y. Design of the reactor and reactor coolant system for qingshan phase II NPP project[J]. Nuclear Power Engineering, 2003, 24(2):1-7. (in Chinese)

[13] 陈文振,于雷,郝建立.核动力装置热工水力[M].北京:中国原子能出版社,2013.

[14] 彭敏俊,田兆斐.核动力装置热力分析[M]. 哈尔滨:哈尔滨工程大学出版社,2012.