关于an±1型正整数竞赛问题的分析*

●

(金华市第一中学,浙江 金华 321015)

在初等数论中，形如an±1(其中a,n∈N+)的正整数有着非常丰富的性质，在各种高中竞赛题中也经常出现.本文主要研究此类正整数竞赛问题以及在构造中的应用.

1 与多项式的关系

从代数角度来看，an±1型正整数容易进行因式分解，因此我们可以将其视为多项式来进行分析.

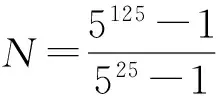
(第32届IMO预选题)

证明令x=525,则

(x2+3x+1)2-5x(x+1)2=

(x2+3x+1)2-526(x+1)2=

[(x2+3x+1)+513(x+1)][(x2+3x+1)-

513(x+1)],

于是N为两个大于1的正整数的乘积，不可能为素数.

2 结合阶以及两个定理的性质

在初等数论中有以下两个重要定理：费马小定理(若素数p不整除a，则ap-1≡1(modp))，欧拉定理(若正整数a,m互素，则aφ(m)≡1(modm)).an±1型正整数与这两个定理以及阶的定义形式相近，因此可利用它们来帮助解题.关于阶的定义及性质在各数论书上都有介绍，这里不作赘述.

例2设n是正整数，Fn=22n+1.设p为Fn的任一素因子，求证：p≡1(mod 2n+1).

证明显然p≠2.设2模p的阶为k，由

22n≡-1(modp),

(1)

得

22n+1≡1(modp),

从而k|2n+1，于是k是2的幂.

设k=2l(其中l∈N,l≤n+1).若l≤n,则将22l≡1(modp)两边同时平方n-l次,得

22n≡1(modp).

再结合式(1)，得 1≡-1(modp),

即p=2,矛盾.因此，l=n+1,即

k=2n+1,

由费马小定理知 2p-1≡1(modp),

故2n+1|(p-1).

注形如Fn=22n+1的数被称为费马数，形如Mp=2p-1的数被称为梅森数，关于它们的素数个数问题仍为未解难题，有兴趣的读者可自行查阅资料研究.

3 结合升幂定理的运用

先给出下面的定理：

定理1若x,y,n∈N+,p为奇素数，(x,p)=1,且p|(x-y)，则

vp(xn-yn)=vp(x-y)+vp(n)，

其中vp(m)表示正整数m中素数p的最高幂次.

证明分两步进行：

1)第一步证明当(p,n)=1时，vp(xn-yn)=vp(x-y).由于xn-yn=(x-y)(xn-1+xn-2y+…+yn-1),x≡y(modp),从而xn-1+xn-2y+…+yn-1≡nxn-1≢0(modp),即不为p的倍数.因此，当(p,n)=1时，

vp(xn-yn)=vp(x-y).

2)第二步证明vp(xp-yp)=vp(x-y)+1.设x-y=kpa(其中a∈N*),(k,p)=1,则

xp-yp= (y+kpa)p-yp=

(kpa)p-1+(kpa)p]-yp=

(2)

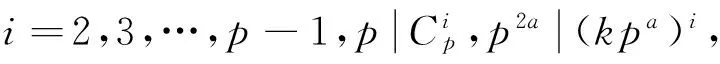
回到定理1，假设n=plm,其中l∈N,(m,p)=1.对l进行归纳：当l=0时，即为第一步证明.假设对l成立,则对l+1的情况,

vp(xn-yn)=vp(xmpl+1-ympl+1)=

vp[(xmpl)p-(ympl)p]=

vp(xmpl-ympl)+1=

vp(x-y)+l+1，

由归纳假设知对l+1亦成立.

综上所述，定理1成立.

类似地，还有以下两个定理：

定理2若x,y,n∈N+,n为奇数,p为奇素数，(x,p)=1,且p|(x-y)，则

vp(xn+yn)=vp(x+y)+vp(n).

定理3若x,y,n∈N+,(x,2)=1,且2|(x-y)，则

v2(xn-yn)=v2(x2-y2)+v2(n)-1.

上述定理被称为升幂定理，它对处理xn±yn型正整数中某些特定素因子的最高幂次有着强大的功能，而an±1型正整数恰为其中的一种特殊情况.

例3[1]求证：存在无穷多个正整数满足：

1)它的各位数字不为0；

2)它可以被它的各位数字之和整除.

(第16届加拿大数学奥林匹克竞赛试题)

v3(An)=v3(103n-1)-v3(10-1)=

v3(3n)+v3(10-1)-v3(10-1)=n,

从而3n|An.而An的各位数字之和为3n,因此An满足条件.显然这样的数有无穷多个.

4 对的素因子分析

对于有关这类数的题目，分析其素因子的情况往往会成为解题的关键和突破口.

(2007年爱沙尼亚国家队选拔考试试题)

1+by+…+by(x-1)≡x(modp),

于是p|x.

又x为n的任意大于1的因数，由上述分析可知n=pm(其中m∈N+)，从而

其中,每一个因数都为p的幂,且大于1,于是

得

bp≡1(modp).

由费马小定理bp-1≡1(modp),知

b≡1(modp),

即

p|(b-1).

p2|(bp-1),

即

bp≡1(modp2).

若m≥2,则

矛盾.因此,m=1，即n为素数.

例5求出所有满足如下条件的正整数m：对于m,存在素数p,使得对任意正整数n,nm-m都不是p的倍数.

(2004年中国国家集训队试题)

从而

p|(mq-1),

即

mq≡1(modp).

若存在正整数n,使nm≡m(modp),则

nmq≡mq≡1(modp)，

(3)

从而(n,p)=1.由费马小定理知

np-1≡1(mod p),

(4)

由式(3)和式(4)，得

n(mq,p-1)≡1(modp).

由qa+1⫮ (p-1),结合式(3)可知

(mq,p-1)|m,

从而

nm≡1(modp),

于是

m≡nm≡1(modp),

即p|q，进而p|m,这与p|(1+m+…+mq-1)矛盾.故对任意正整数n,p⫮nm-m.

5 在构造中的应用

例6[1]设p是一个素数.证明：存在无穷多个正整数n,使得pn+1是素数.

(第18届韩国数学奥林匹克竞赛试题)

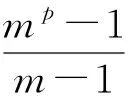
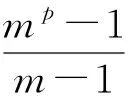
即q|p,从而q=p.而0≡mp-1≡-1(modp),矛盾.因此，q与m(m-1)互素.

回到原题,用反证法.

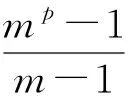
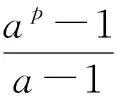
[1] 沈文选,张垚,冷岗松．奥林匹克数学中的数论问题[M]．长沙：湖南师范大学出版社，2015．