也谈对称函数中求和问题的教学策略*

●

(增城中学,广东 广州 511300)

对称是数学中的重要概念之一，一般是指在某种变换下保持的不变性，例如图形的轴对称或中心对称、数学结构的对称等.通过对称可看出数学与自然、生产和艺术之间存在着密切的关系，对称符合自然规律，满足生产需求，也顺应审美标准.正是因为如此，以对称为命题立意的题目广泛存在于各种试题中，且经久不衰.其中，利用函数的对称性质来解决求和问题是中学数学中常见的重点和热点问题之一.笔者对此类问题略作梳理，提出了初步的教学策略，并作简单的教学反思，权当抛砖引玉.

1 通过数形结合和特殊化思想引导学生理解对称函数的性质表征

性质1若函数f(x)关于直线x=a对称，则有f(a-x)=f(a+x)，反之也成立.

这是最容易理解的对称性质，教师引导学生分析a-x与a+x在坐标轴上与a的距离相等，f(x)关于直线x=a对称，即f(a-x)=f(a+x).

性质2若函数f(x)关于直线x=a对称，则有f(x)=f(2a-x)，反之也成立.

性质2是性质1的变式，此时要引导学生注意x和2a-x的位置关系.

性质3若函数f(x)关于点(a,0)对称，则有f(a-x)=-f(a+x)，反之也成立.

对比性质1，f(a-x)=-f(a+x)意味着将轴对称图形的一半翻折下来，变为关于点(a,0)对称.

性质4若函数f(x)关于点(a,0)对称，则有f(x)=-f(2a-x)，反之也成立.

教师让学生对比性质2自己判断性质3和性质4.

性质5若有f(a-x)+f(a+x)=2b，则函数f(x)关于点(a,b)对称，反之也成立.

根据中点坐标公式，设点P(a-x,f(a-x))，Q(a+x,f(a+x))，则PQ的中点坐标为

由f(a-x)+f(a+x)=2b,得

从而中点M的坐标为(a,b).由x的任意性知点P,Q恒关于点(a,b)对称，即函数f(x)关于点(a,b)对称.将性质5特殊化，令b=0即得性质3的结论.

以上性质均可用具体的函数图像来加以辅助说明，例如轴对称问题可找二次函数，点对称问题可找三角函数.

2 通过设置问题链引导学生分类归纳常见对称函数的类型及处理思路

1)反比例型对称函数.

( )

A.0 B.mC.2mD.4m

(2016年全国数学高考卷Ⅱ理科试题第12题)

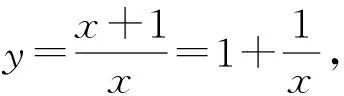
(y1+y2+…+ym)=m.

也可引导学生将f(x)这个对称函数特殊化，例如设f(x)=x+1，后面的求解就简单了.

例2方程2(x-1)sin πx+1=0在区间[-2,4]内的所有解之和等于______.

(2012年全国数学联赛吉林省预赛试题第8题)

分析2(x-1)sin πx+1=0可化为

2)三次(高次)函数型对称函数.

事实上所有的三次函数都是中心对称函数，高次函数能否成为对称函数则需具备一定的特殊性.教学中宜设置适当难度的问题，由特殊到一般、由浅入深，逐步引导学生认识对称函数的庐山真面目.

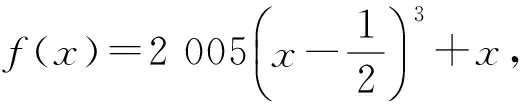
(2015年复旦大学自主招生数学试题第1题)

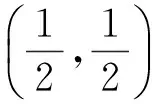
f(x)+f(1-x)=1，

从而

( )

A.0 B.504 C.1 008 D.2 016

(2017年广东省广州市第一次数学模拟测试理科试题第12题)

因此

例5例3和例4中的三次函数均为中心对称函数，那么任意的三次函数f(x)=ax3+bx2+cx+d是否都为中心对称函数？

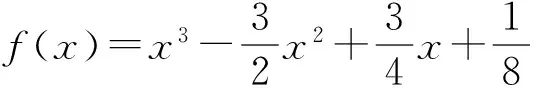
如何证明？类比例4，思路1是将f(x)中的二次项通过二项式定理隐藏起来，即

f(x)=ax3+bx2+cx+d=

( )

A.1 B.2 C.4 D.8

分析观察f(x)的形式，容易发现

f(x)=f(1-x)，

f′(x)=-5(1-x)4+5x4，

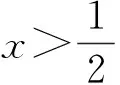
有了对称性，目标S易求得.

3 从导函数的角度归纳总结对称函数的判断方法

结论1[1]可导函数y=f(x)的图像关于点(a,f(a))对称的充要条件是其导函数f′(x)的图像关于直线x=a对称(注：f(x)在x=a处有意义).

证明先证必要性.若可导函数y=f(x)的图像关于点(a,f(a))对称，则

f(a-x)+f(a+x)=2f(a).

两边求导，由复合函数的求导法则知

-f′(a-x)+f′(a+x)=0，

即

f′(a-x)=f′(a+x)，

从而导函数f′(x)的图像关于直线x=a对称.

再证充分性.若导函数f′(x)的图像关于直线x=a对称，则

f′(a-x)=f′(a+x).

两边积分，得

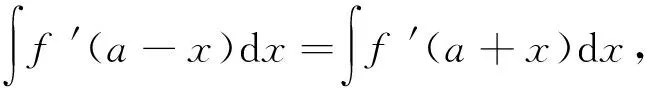
从而

-f(a-x)=f(a+x)+C.

令x=0，则C=-2f(a)，从而

f(a-x)+f(a+x)=2f(a)，

于是y=f(x)的图像关于点(a,f(a))对称.

结论2可导函数y=f(x)的图像关于直线x=a对称的充要条件是其导函数f′(x)的图像关于点(a,0)对称(注：f(x)在x=a处有意义).

结论2的证明方法与结论1类似，可让学生自行完成证明.

得到了这两个结论，教师可以让学生小试牛刀，找具体函数再次验证.例如f(x)=sinx关于(π,0)对称，其导函数f′(x)=cosx确实关于直线x=π对称.

4 几点反思

1)准确理解对称函数的表现形式是学会求和的先决条件.学生容易判断简单并且具体的初等函数的对称性，但对于抽象函数，基础较弱的学生理解起来有一定的困难，例如容易将f(a-x)=f(a+x)与f(x-a)=f(a+x)所代表的意义搞混淆，将f(a-x)=f(a+x)变成f(a-x)=f(b+x)就看不出对称性等.因此,在教学中首先要抓住对称函数本身具备的图像对称特征，数形结合，并结合具体函数验证，强化学生对对称函数的认识.

2)应循序渐进，螺旋上升.从f(a-x)=f(a+x)到f(x)=f(2a-x)，再到f(a-x)+f(a+x)=2b，需要逐步引导.而对于三次函数的对称性问题，不宜一下跳到用导数的观点来强行灌输，应有问题设置和方法引导方面的层层铺垫，经特殊到一般，方能水到渠成.

[1] 侯宝坤.导函数与原函数对称性的联系[J].数学通讯,2006(5):14.