例析三角函数中的易错点刘
2018-05-08 09:51刘博文
中学生数理化·高一版 2018年4期
■刘博文
三角函数的公式多、概念广,解题方法与技巧多样,所以经常会出现忽视讨论、遗漏条件、忽视取值范围等思维误区。下面就解题中容易出现的易错点进行举例分析,供大家学习与参考。
易错点1:忽视对整数k的讨论
错解分析:忽视对整数k的奇偶性的讨论导致出错。
由4kπ+2π<2α<4kπ+3π,k∈Z,可知2α是第一、二象限角或2α的终边落在y轴的非负半轴上。
易错点2:忽视对参数的讨论
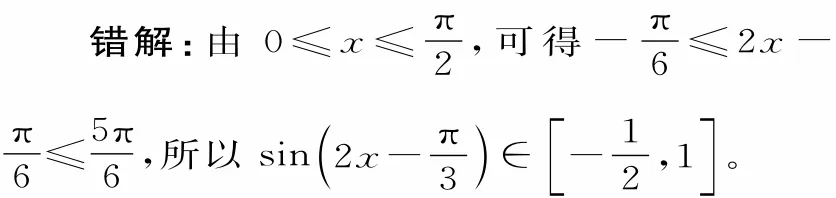
错解分析:上述解法缺少分类讨论的意识,从而导致了漏解。

易错点3:忽视角的取值范围

所以(sinθ-cosθ)2=1-2sinθcosθ=
错解分析:上述解法忽视了角θ的取值范围。事实上,由0<θ<π,可以确定sinθcosθ的取值符号。
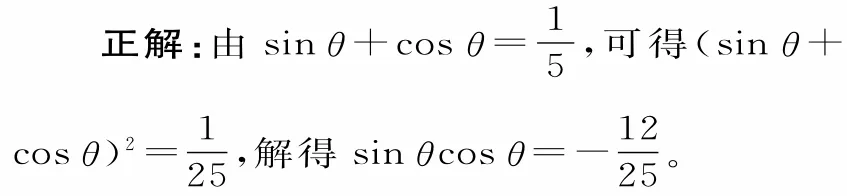
所以(sinθ-cosθ)2=1-2sinθcosθ=。
误区4:忽视同角三角函数之间的内在联系
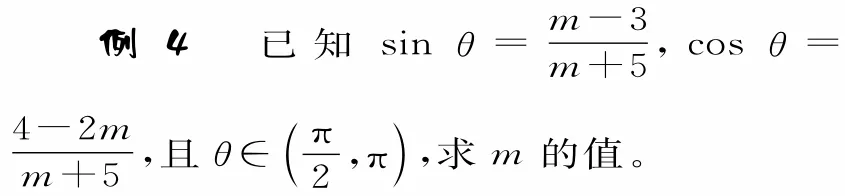

综上可得,m=8。
易错点5:三角函数图像变换中忽视整体变量观念致错
A.先将每个x值扩大到原来的4倍,y值不变,再将横坐标向右平移个单位
C.先将每个x值扩大到原来的4倍,y值不变,再将横坐标向左平移个单位
错解分析:上述解法缺少整体变量的观念致错。
函数y=sin2x的图像;再将y=sin2x图像的纵坐标不变,横坐标向右平移个单位,得到像。应选D。
猜你喜欢
中学生数理化·七年级数学人教版(2022年6期)2022-06-05
初中生学习指导·中考版(2022年3期)2022-03-25
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
新课程·上旬(2020年36期)2020-12-29
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
中学生数理化·七年级数学人教版(2020年4期)2020-08-10
中等数学(2018年12期)2018-02-16
小朋友·快乐手工(2009年5期)2009-06-11
初中生·作文(2004年9期)2004-09-18

