基于几何画板的数学探究性学习的设计与实现—《正弦定理》教学设计与评析

杜丹丹 李孝诚

摘要：基于几何画板，结合数学知识本质，该文巧设问题串，构建了动态探究平台，有效激发学生的数学思维，让学生经历“抽象—猜想—证明（验证）”过程，有效建构正弦定理，积累数学活动经验。

关键词：正弦定理；边角关系；解三角形

中图分类号：G64 文献标识码：A 文章编号：1009-3044（2018）08-0094-02

《正弦定理》是人教A版数学必修五第一章“解三角形”中的第1小节“正弦定理和余弦定理”的第1课时，主要包括正弦定理的探究、证明及应用等内容。“正弦定理”是对初中“解直角三角形”内容的延续，是基于已学习过的三角知识，通过对三角形边角关系的探究，揭示任意三角形边角之间的一种定量关系。除此之外，它与之后的余弦定理都是解三角形的重要工具，也是解决实际生活问题的有效工具。

学生已经学习过平面向量与三角函数相关的内容，具有一定的观察与分析问题的能力。但新旧知识之间联系的不足，也可能使学生陷入一种思维障碍，这就需要教师恰当的引导与提示，尽量启发学生，引导他们自主地发现问题、提出问题、分析问题和解决问题。

1发现问题，引出课题

问题1：请同学们观察老师手中的三角板，可以看到，三角板的一个角已经破损，你们能根据已知的两个角及一边长，确定破损角的大小及破损两边的长度吗？

追问：还有其他的方法吗？能否将这里的三角板抽象成我们熟悉的几何图形来处理？

接下来通过操作几何画板，将实物三角板抽象转化成三角形。

问题2：猜想在任意的三角形中都存在怎样的边角关系。

评析：基于学生初中阶段学习过的“解直角三角形”的知识，提出问题1，让学生经历“观察和思考”的过程，利用点与线、边与角之间的关系自主解决问题。通过问题2的创设，引导学生回忆有关三角形边角关系的内容，设置思维的突破点，把本节课研究的焦点聚集到“三角形的边角关系”的问题上，从而为引出本节课题做好铺垫。

2分析问题，探究新知

2.1归纳发现

問题3在任意AABC中，它的三边a，b，c与对应的三角A，B，C存在怎样的关系？

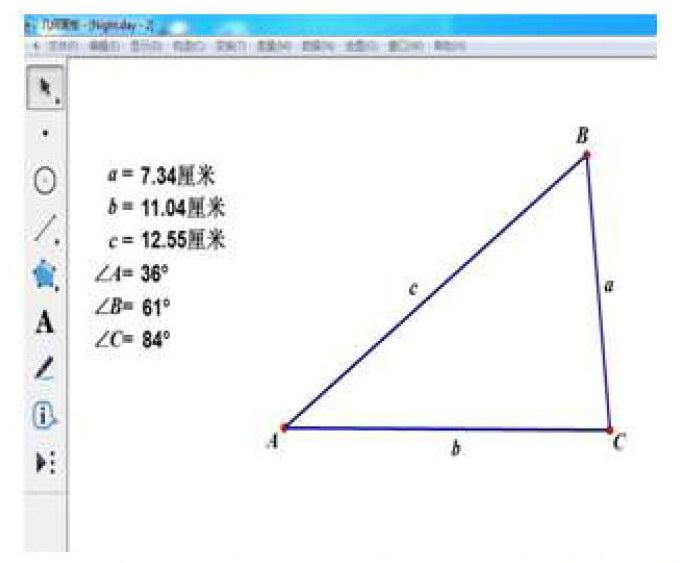
利用几何画板改变任意△ABC的边长与角度大小，让学生观察边长与角度改变时，数值之间的联系，如图1所示。

让学生尽可能多地归纳出三角形的边角关系，引导学生发现其中对探究本课最具有价值的边角关系。

评析：提示学生回顾以前学习的知识，观察几何画板中边与角间数值的联系，归纳三角形的边角存在怎样的关系。引导学生想起“大边对大角，小边对小角”的边角关系，由此将三角形中的边与角联系起来，为探寻下一步的边角关系设置好突破口。

2.2提出猜想

在学生提出的众多的三角形的边角关系中，将“大边对大角，小边对小角”的边角关系，写成数学语言表达的形式（此处将角作为弧度制处理）：

此时，共得到以上四种关于三角形边角关系的猜想。

评析：由三角形的对称美、和谐美，引发学生探究其数式结构是否也具有同等程度的美。将“大边对大角，小边对小角”的边角关系写成对称的等式形式，是学生需要解决的思维突破口。将猜想1作为先行组织者，引导学生通过适当的变换得到猜想2、猜想3和猜想4。

2.3验证猜想

问题4验证上一步中的四个猜想是否对所有的三角形都成立。

（1）对等边三角形来说，猜想1、猜想2、猜想3、猜想4均成立；

（2）对等腰直角三角形来说，只有猜想2成立；

（3）对任意直角三角形来说，只有猜想2成立；

（4）假设猜想2对于任意三角形均成立。接下来需要证明。

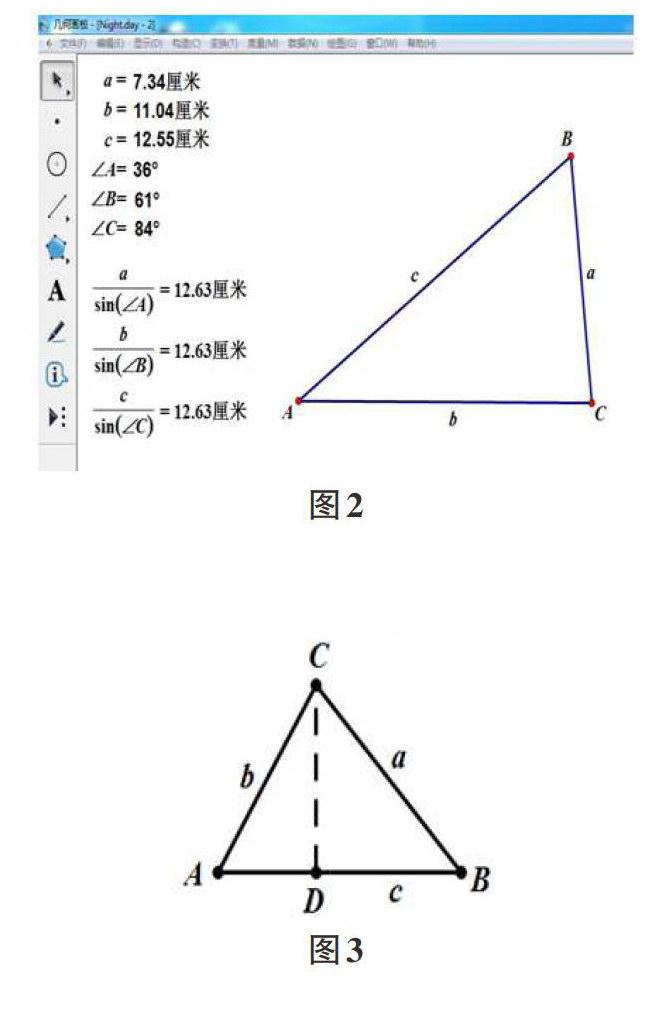
首先用几何画板动画展示验证猜想2：在任意一个△ABC中，无论三个角∠A，∠B，∠C和三条边a，b，c如何变化，猜想2都成立，如图2所示。

接下来用数学方法证明猜想2：

①对任意锐角三角形，证明猜想，如图3所示：

由第1步中对直角三角形的验证猜想，将问题转化为熟悉的情境，做AB边上的垂线CD，由此可得到两个直角三角形：

在R△ACD和Rt△ABCD中，存在一个公共的直角边CD。

在砌ACD中，有CD=bsinA；

在△BCD中，有CD=asinB；

②对任意钝角三角形来说，猜想2仍然成立，具体证明交给同学们课下完成。

2.4得出结论

综上，引导学生总结出正弦定理的内容：

在一个三角形中，各边和它所对角的正弦的比相等，即

一般地，把三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形。

评析：给出正弦定理的完整表述，说明解三角形的概念，便于同学们接下来利用正弦定理解三角形。