机翼调姿对接运动仿真技术研究

徐源，沈建新

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

飞机大部件对接是飞机总装阶段的关键部分，大部件对接技术是一项涉及许多领域的综合性技术[1]，其中翼身对接是飞机大部件对接的重要环节，其很大程度上影响着飞机装配质量、制造安装成本和生产周期。传统的型架手工装配已很难满足这些要求，数字化、柔性化、自动化已成为飞机大部件对接技术的发展趋势[2]。

装配运动仿真技术对飞机装配发挥着重要作用，通过在虚拟环境中进行装配体和工装的建模、计算、仿真验证，能提前发现和解决实际装配中可能出现的问题[3]。将其运用在机翼调姿对接过程中，可以实现调姿对接轨迹规划检验，减少工装在设计阶段可能出现的问题，提高装配效率。

本文采用3个三轴定位器搭建调姿对接模型，利用CATIA DMU运动仿真模块的分析结果评估机翼调姿对接过程中的运动稳定性，为实际的翼身自动调姿对接做好前提准备。

1 机翼调姿对接概述

1.1 机翼调姿对接流程

机翼调姿对接可以抽象为刚体位姿调整的问题[4]，即最终实现机翼从初始位置到目标位置调整的过程。调姿对接过程由多个模块共同协调完成，包括测量模块、计算模块、控制模块、定位器模块、检测反馈模块等。测量模块用于调姿对接过程中机翼表面测量点的测量，将测量点信息导入计算模块，完成机翼空间位姿的测定和定位器驱动的逆解，并通过控制模块完成对定位器模块的驱动，实现机翼调姿对接。调姿对接流程如图1所示。

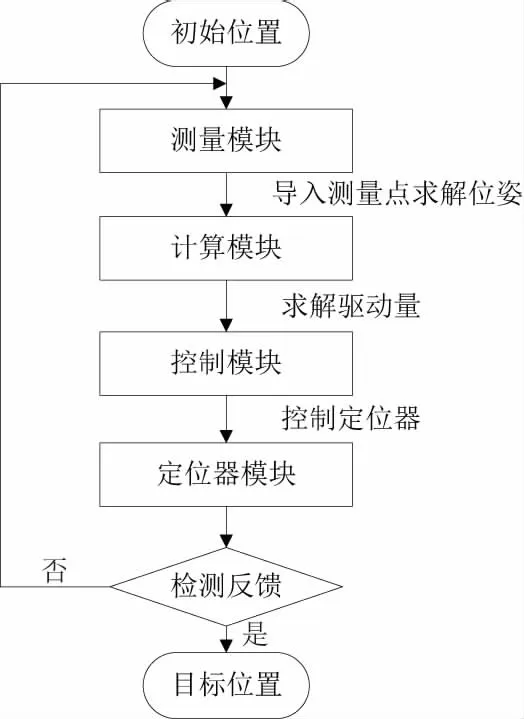
图1 调姿对接流程图

1.2 调姿定位器介绍

机翼调姿对接过程中，通常采用三轴定位器调姿。三轴定位器是一种伺服驱动装置，它既可以做为机翼调姿对接过程的调整单元，也是调姿对接全生命周期的支撑单元[5]。能够实现x、y、z三个方向的平移运动，由x方向基座、y方向滑块、z方向伸缩柱和工艺接头组成的结构原理图如图2所示。通过控制三轴定位器各个方向的运动，实现机翼在对接过程中空间6个自由度位姿调整[6]。

图2 三轴定位器原理图

2 调姿对接运动仿真

2.1 运动仿真模型搭建

运动仿真需要完成机翼在空间的调姿对接过程，其姿态和位置的调节共有6个自由度需要限制，并且需要不共线的3点支撑才能保证其约束的完备性。因此调姿对接运动仿真的最基本要求是实现机翼的6个自由度调节，这里通过使用3个三轴定位器来完成整个机构的运动。整个机构包括3个运动支链，每个支链由3个滑移副和1个球铰副组成。根据多刚体系统自由度计算公式：

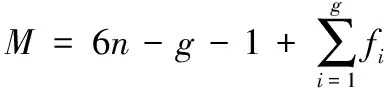
(1)

其中：n为总构件数，g为运动副数，fi为各运动副的自由度数(滑移副为1，球铰副为3)，可以求得整个调姿机构的自由度数为：

M=6×(11-12-1)+(9+3×3)=6

(2)

在CATIA DMU运动分析模块中，只有自由度为0的机构才能进行运动模拟[7]，通过运动副和驱动的添加都能减少机构的自由度，运动副已经确定，只需添加6个驱动即可。可以采用3-2-1的定位器驱动方式[8]，即第1个定位器为三驱动定位器，第2个定位器为两驱动定位器，第3个定位器为单驱动定位器。

根据某型飞机和定位器的数学模型以及二者的位置关系，在CATIA下建立自动调姿对接运动模型。模型包括：机翼、三轴定位器模型(图3)。模型间的运动接合关系包括定位器各轴上的平移接合以及工艺球头的球铰接合等，如表1所示。

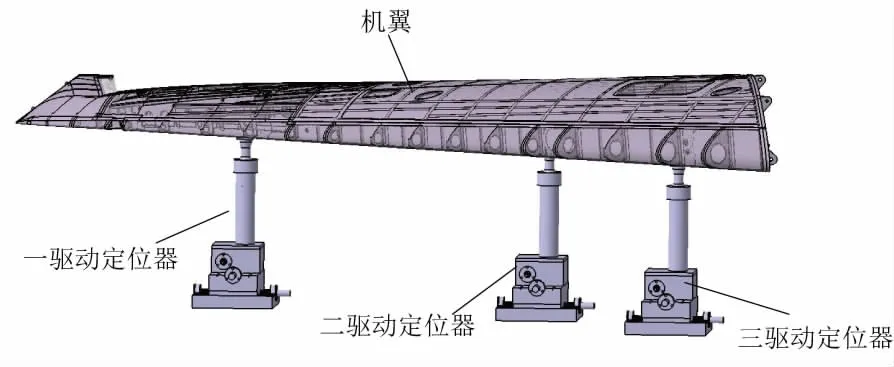
图3 机翼和定位器仿真模型

2.2 调姿运动轨迹规划

根据上述可知，机翼的空间位姿由6个参数量决定，分别是机翼局部坐标系相对于基准坐标系的3个平移量x,y,z和3个旋转量α,β,γ，完成这6个参数的调整，即可完成整个调姿过程。

机身的调姿可以直接由定位器完成这6个参数的调整，但是在机翼调姿对接调姿中，考虑到机翼可能会和机身的叉耳出发生碰撞，将机翼的调姿对接分解成如下3个阶段进行。

a) 完成机翼姿态3个欧拉角α,β,γ调整；

b) 完成0,y,z方向位置调整；

c) 完成x,0,0 方向上翼身对合过程。调姿对接流程如图4所示。

图4 机翼调姿对接流程规划

在工程实践中，实现对上述流程的具体规划，除了获得了已知的初始位姿和目标位姿，还应要求每个调姿阶段的初始速度和终止速度为0。另外，为了使调姿运动光滑连续，还应保证每个阶段的初始加速度和终止加速度为0。在对机翼对接进行运动仿真时，可采用五次多项式拟合来满足上述要求[9]，即：

Lt=m5t5+m4t4+m3t3+m2t2+l0

(3)

1) 机翼初始位姿、目标位姿约束条件：

(4)

2) 机翼速度约束条件：

(5)

3) 机翼加速度约束条件：

(6)

其中L(t) 为机翼关于时间t的函数,T为调姿时间,l0、lT分别为调姿的初始位置和目标位置。将式(4)、式(5)、式(6)的约束条件代入至式(3)方程中，可以解得机翼调姿对接五次多项式的轨迹方程为：

(7)

2.3 仿真驱动求解

由于三轴定位器接头和机翼机身属于刚性连接，定位器接头的球心在机翼的局部坐标系位置固定。因此，通过上述调姿轨迹规划的轨迹方程可逆解出3个定位器的在对接坐标系中的运动轨迹，从而确定3个定位器各个驱动轴的驱动量。

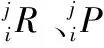
(8)

(9)

其中c 表示cos ，s 表示sin 。

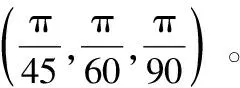
图5 定位器位移量曲线

2.4 运动学仿真分析

根据上述轨迹规划逆解出的定位器驱动轨迹，将其导入至已经建立好机翼调姿对接运动仿真模型的CATIA DMU模块，并在各个命令接合处添加编辑公式来应用驱动的轨迹。通过激活检测传感器，测量机翼在运动仿真中速度和加速度变化曲线。由于所测得的线性加速度只有大小，为了符合线性速度变化规律，将加速度曲线导出为EXCEL表格并修改，最终获得符合速度变化规律的加速度曲线。如图6、图7所示。

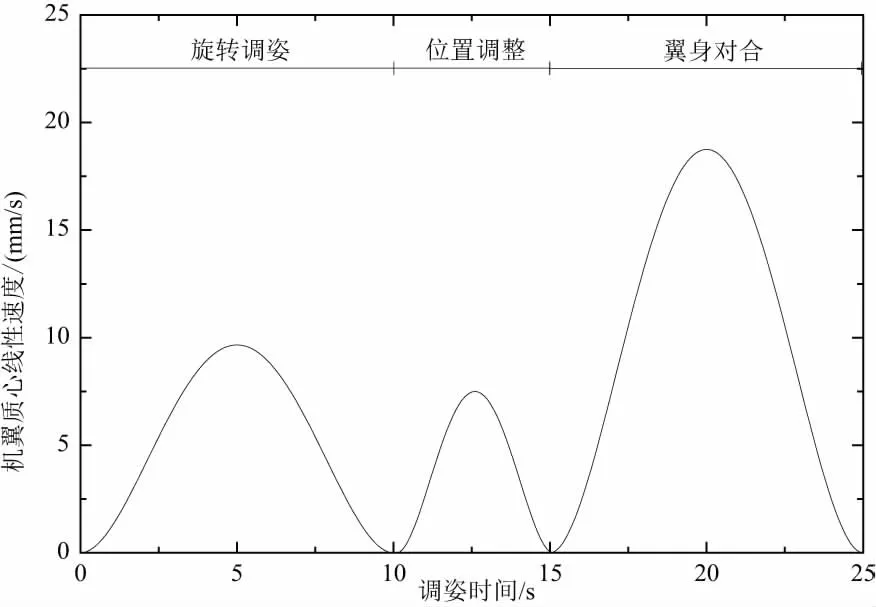
图6 机翼质心线性速度随曲线

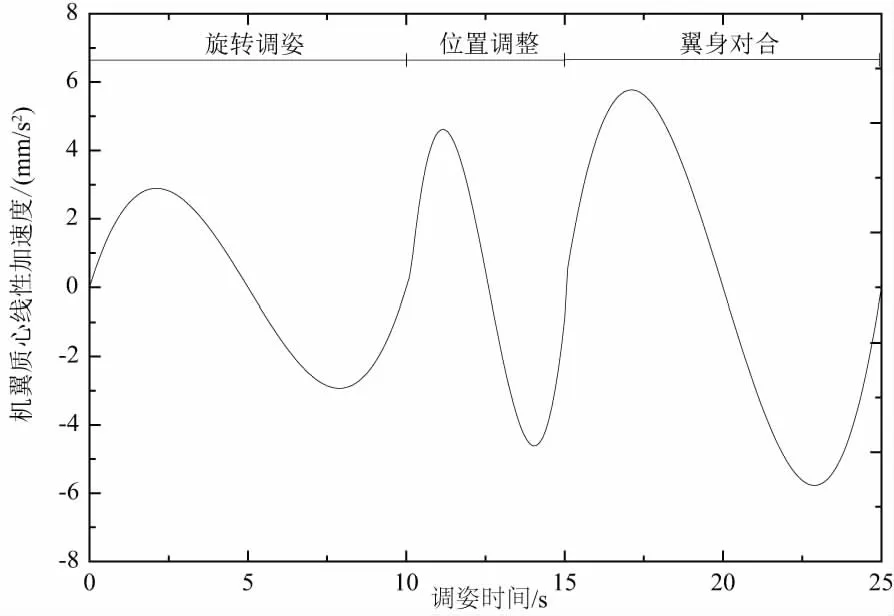
图7 机翼质心线性加速度曲线

由此可以看出在机翼调姿对接过程中速度的最大值为18.75 mm/s，发生在15 s～25 s的翼身对合过程中，加速度的最大绝对值为5.69 mm/s2，也发生在翼身对合过程中。并且在每个阶段调姿过程中其速度和加速度曲线都较为平整光滑，数值没有突变，仿真结果表明，按照上述轨迹规划，机翼调姿对接运动能够平稳进行。

3 结语

利用CATIA软件建立翼身调姿对接运动仿真模型，并将整个调姿对接过程分成旋转调姿、位置调整、翼身对合3个阶段，并根据五次多项式方程完成对机翼调姿对接的轨迹规划。按照3个阶段和轨迹规划逆解出驱动器驱动量，对整个调姿过程进行运动仿真，测量出机翼在调姿对接过程中的速度和加速度随时间变化曲线。仿真结果表明：机翼调姿对接可按预期轨迹平稳光滑的从初始位置移动至目标位置，且机翼速度、加速度没有出现突变，验证了轨迹规划的合理性，可为以后定位器运动控制、控制系统设计以及调姿对接轨迹优化奠定基础。

参考文献:

[1] 范玉青. 飞机数字化装配技术综述——飞机制造的一次革命性变革[J]. 航空制造技术, 2006 (10): 42-48.

[2] 许国康. 飞机大部件数字化对接技术[J]. 航空制造技术，2009(24): 42-45.

[3] 李惠, 张林鍹, 肖田元, 等. 基于仿真控制的飞机大部件对接原型系统研究[J]. 航空制造技术, 2013(22):90-94.

[4] 张进华, 王永园. 基于等效并联结构的大部件姿态调整平台设计与轨迹规划[J]. 机床与液压，2011(7):1-5.

[5] 盖宇春, 朱伟东, 柯映林. 大型飞机总装配中支撑点设计分析技术[J]. 浙江大学学报(工学版)，2013(12):2176-2183.

[6] Bin ZHANG, Bao-guo YAO, Ying-lin KE, et al. A novel posture alignment system for aircraft wing assembly[J]. 浙大学报(英文版), 2009, 10(11):1624-1630.

[7] 盛选禹, 李明志, 包支. 等. CATIA V5 r21运动分析教程[M]. 北京: 机械工业出版社, 2015: 71-90.

[8] 黄翔, 李泷杲, 陈磊, 等. 民用飞机大部件数字化对接关键技术[J]. 航空制造技术，2010(3):54-56.

[9] 乐英, 岳艳波. 六自由度机器人运动学仿真及轨迹规划[J]. 组合机床与自动化加工技术, 2016(4):89-92.

[10] 邹爱丽, 王亮, 李东升, 等. 数字化测量技术及系统在飞机装配中的应用[J]. 航空制造技术, 2011(21):72-75.