融合二维图像和三维点云的相机位姿估计

周佳乐，朱兵，吴芝路

（哈尔滨工业大学 电子与信息工程学院，黑龙江 哈尔滨 150001）

1 引言

相机位姿估计是机器人应用、自主导航以及增强现实中的关键技术，其目的是通过当前相机所采集的图像信息，以及已知环境的先验信息，来估计出当前相机设备在三维真实场景中的位置和姿态，由于相机的位姿信息包含六个自由度，因此也称为相机的六自由度估计。随着自动驾驶、精确定位导航等领域对定位的精度要求不断提高，仅仅使用二维图像已经无法对现实的三维世界进行准确描述，因此包含深度信息的三维场景点云成为了定位技术更为关注的重点，通过三维场景点云以及图像处理的相关算法可以实现更加精确的应用，这也成为了相机位姿估计技术的一个发展方向。

近年，相机位姿估计技术在国内外发展迅速，传统的相机位姿估计方法首先采用SFM（Structure From Motion）算法对图像数据库构建三维点云数据，同时将每一个3D点云与特征算子相关联。对于查询图像，提取其特征描述子并与三维点云匹配，使用PnP（Perspective-n-Point）位姿求解算法解得最终的位姿［1-4］。这种方法称为基于结构的相机位姿估计。然而这种方法存在较大局限，一旦点云与特征描述符的关系确定，对于位姿查询图像，只能提取特定的特征描述符来进行2D-3D匹配，这种构建2D-3D匹配点的思路在关联特征描述符不易提取的情况下表现往往较差。因此本文结合图像检索的思路与特征匹配算法，充分利用深度图像信息，在2D-3D匹配点构建思路上进行改进；同时提出位姿优化目标函数，对PnP位姿解算的结果进行进一步优化，提出多阶段的相机位姿估计方法。

随着深度学习方法的广泛应用，大量学者投身于采用深度学习的方式来解决相机位姿估计问 题。Kendall等 人［5］将GoogleNet网 络 进 行 改进，使用神经网络直接预测相机的六自由度位姿，然而该方法最终的相机位姿估计精度较低，文献［6］进一步证明了直接使用神经网络估计相机位姿的方法准确率只能逼近使用图像检索的方法［7］。Li等人［8］通过孪生神经网络来拟合查询图像与参考图像之间的相对位姿关系，进一步实现相机的位姿估计，由于图像中并不包含场景的三维场景信息，因此单独使用图像进行位姿估计的误差较大。Tang等人［9］利用深度检索算法得到参考图像，在查询图像与参考图像之间构建一个损失向量训练神经网络并获得稠密场景匹配，进一步实现相机位姿估计，其本质是采用神经网络拟合查询图像与参考图像的关系，因此前端图像检索中存在较大误差时，其位姿估计精度往往较差。总之，目前将神经网络模型直接用于相机位姿估计的端到端学习方式，由于网络模型参数的有限性，无法完全拟合所有的三维场景信息，导致其位姿估计结果的精度较低或速度较差。为实现更加精确且高效的相机位姿估计方法，本文将深度学习算法用于传统基于结构的相机位姿估计算法当中，设计卷积神经网络用于获得更为稠密的2D-3D匹配点，提出基于稠密场景回归的多阶段相机空间位姿估计方法，以此提高相机位姿估计算法的精确性。

2 数据集的构建

不同的真实场景对相机位姿估计算法精度的影响较大，为推进特定场景下相机位姿估计算法的研究，本文首先构建相机位姿估计数据集。

2.1 像素坐标与世界坐标关系

本文基于二维图像和三维点云对单目相机进行空间位姿估计，数据集中包含了单目相机的RGB图像以及RGB图像所对应的三维空间坐标信息。在三维图像处理中要考虑到2个三维坐标系和2个二维坐标系。这4个坐标系互相嵌套，相机坐标系以世界坐标系为基础，图像坐标系以相机坐标系为基础，像素坐标系则以图像坐标系为基础。世界坐标系一旦确定则不会变化，而相机坐标系一直相对世界坐标系发生变换，图像坐标系则相对相机坐标系保持稳定不变。图1为各个坐标系之间的关系：

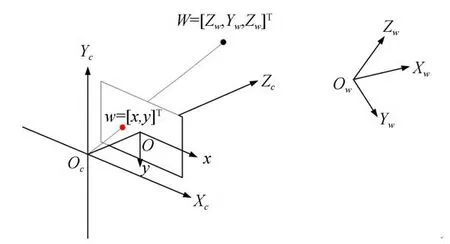
图1 各坐标系间的关系Fig.1 Relationship between coordinate systems

图中，Ow-Xw，Yw，Zw为世界坐标系，原点可以认为是相机的真实世界坐标；Oc-Xc，Yc，Zc为相机坐标系，原点为相机的光心；o-x，y为图像坐标系。

3个坐标系的变换关系可以通过外参矩阵以及内参矩阵来进行描述，外参矩阵是相机相对起始点的位置与姿势的变化，用来描述世界坐标系和相机坐标系之间的转换关系；内参矩阵是相机本身的固定参数，是指相机坐标系下的物体投影到图像平面下的内部参数，通常用来描述相机坐标系和图像坐标系之间的关系。通过坐标系关系转换，可以得到像素坐标系与世界坐标系的关系为：

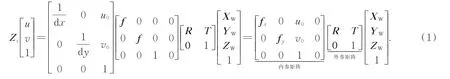
在这种转换关系中，内参矩阵可以通过相机标定的方式精准获得，在相机应用环境不发生变化时，可认为其不发生变化。然而，在相机位姿发生变化时，其外参矩阵也将发生变化。本文的目标是通过模型估计出当前相机的外参矩阵，因此数据集中包括相机所获得的RGB图像（像素坐标）、RGB图像所对应的相机外参矩阵以及相机所处场景的三维真实场景信息（世界坐标）。

2.2 SFM三维重建

通过分析像素坐标和世界坐标之间的关系，可以知道构建数据集的关键是获得单张RGB图像的外参矩阵以及相机所处场景的三维真实场景。本文采用SFM算法对相机所拍摄场景进行三维重建，并获得重建后每一张RGB图在三维场景中的外参信息。SFM算法是一种基于各种收集到的无序图片进行三维重建的离线算法，通过相机的移动采集不同视角的图像，求解相机的相对位姿信息并恢复出场景的三维信息。通过SFM算法，可以求解得到每一张RGB图像的三维稀疏点云数据以及其相对于该三维稀疏点云下的位姿信息，图2是采用该算法进行三维重建的效果示意图（彩图见期刊电子版），图中红色轨迹为每一张RGB图像所对应的真实相机位姿，黑色点为三维稀疏点云：

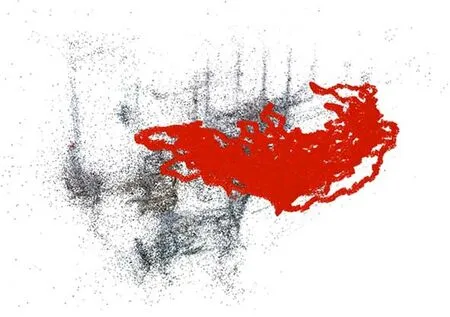
图2 三维稀疏点云重建及位姿数据集构建Fig.2 3D sparse point cloud reconstruction and pose dataset construction

基于SFM算法进行三维重建的三维点云是由特征匹配所提供的，由于这些匹配点的提取是稀疏的，因此采用SFM算法进行三维重建得到的点云数据也将是稀疏的。为了研究更加精准的位姿估计算法，本文在构建数据集的时还需产生稠密的点云数据。SFM算法可以解算得到每一帧RGB图像在当前三维稀疏点云下的位姿矩阵，为得到图像的稠密三维坐标信息，还需要采用深度相机同步采集每一帧RGB图像的深度信息［10］，通过前述三维重建过程中得到的位姿以及坐标间的变换关系，求解出场景的稠密三维点云。本文实验使用Astra Mini深度相机作为RGB图像以及深度图像采集设备。经过实际标定实验，该深度相机的深度有效测量范围为0.6～8 m，其精度为±(1～3)mm/m，深度图像数据为16位深度值，其深度值为相机与物体的实际距离，单位为mm。由于实验中不可避免存在无效的测量深度值（深度图像中黑色边缘部分），在实际实验过程中，将有效深度值对RGB图像进行掩摸处理，舍弃无效的深度值。本文对实验室进行采集，最终重建的结果如图3所示。

图3 稠密点云数据构建Fig.3 Dense point cloud data construction

通过以上方法，构建得到最终的数据集，该数据集包含4 000张RGB图像、深度图以及每张RGB图像对应的位姿信息，本文采集的数据为连续帧图像，将图像以1 000帧为单位划分为4个序列，其中1，3序列作为训练集，2，4序列作为测试集，具体信息如表1所示。

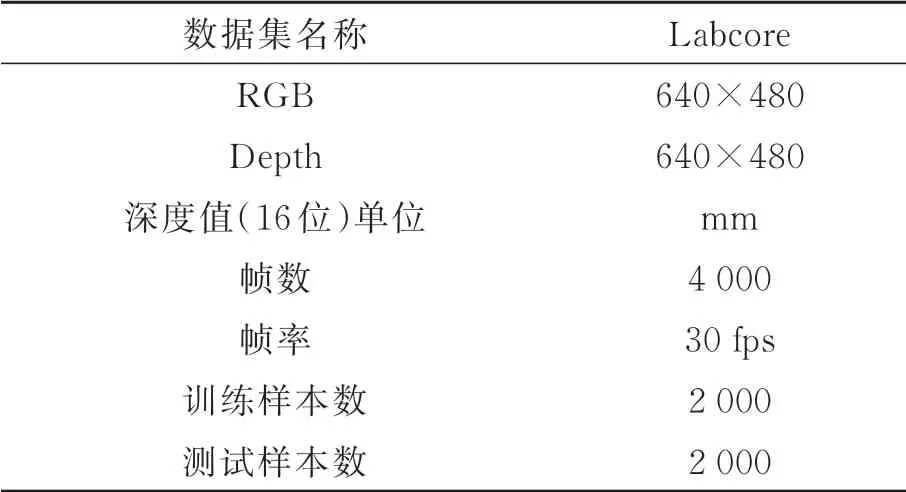
表1 Labcore数据集Tab.1 Detail of labcore dataset

3 多阶段相机位姿估计

传统基于结构的相机位姿估计方法是找到2D-3D匹配点，通过PnP位姿求解算法求解方程，以解算得到当前相机的具体位姿［1-4］，该方法在构建点云数据时将3D点与特定的2D特征点进行关联，一旦数据构建完成，其特征描述符便无法更换，而不同场景下采用不同特征描述符所得的位姿估计结果差异较大，这也成为其在特征描述符不易提取的环境中表现较差的主要原因。因此本文首次将图像检索算法引入2D-3D匹配点的构建当中，并采用传统基于结构算法的相机位姿估计思路，同时构建目标函数优化位姿估计结果，提出基于多阶段的相机位姿估计方法，该方法结合图像检索方法与基于结构相机位姿估计方法的优势，提升了2D-3D匹配点的匹配速度与精度，具体过程为：第一阶段，构建2D-3D匹配点，采用深度图像检索算法检索出查询图像的最近邻帧作为参考图像，通过特征匹配算法及坐标映射关系找到用于位姿解算的2D-3D匹配点；第二阶段，粗位姿求解并剔除外点，使用PnP位姿求解算法求解相机位姿，对求解得到的位姿进行评分，采用随机抽样一致（Random Sample Consensus，RANSAC）算法的思路剔除误匹配点，得到初始位姿估计；第三阶段，位姿对齐优化，将前一阶段求解的位姿作为初始位姿，设计目标函数，用三维点云将查询图像位姿与参考图像位姿对齐，采用最小二乘法对初始位姿估计结果进行进一步优化，得到最佳位姿估计结果。图4是整个算法的流程图。

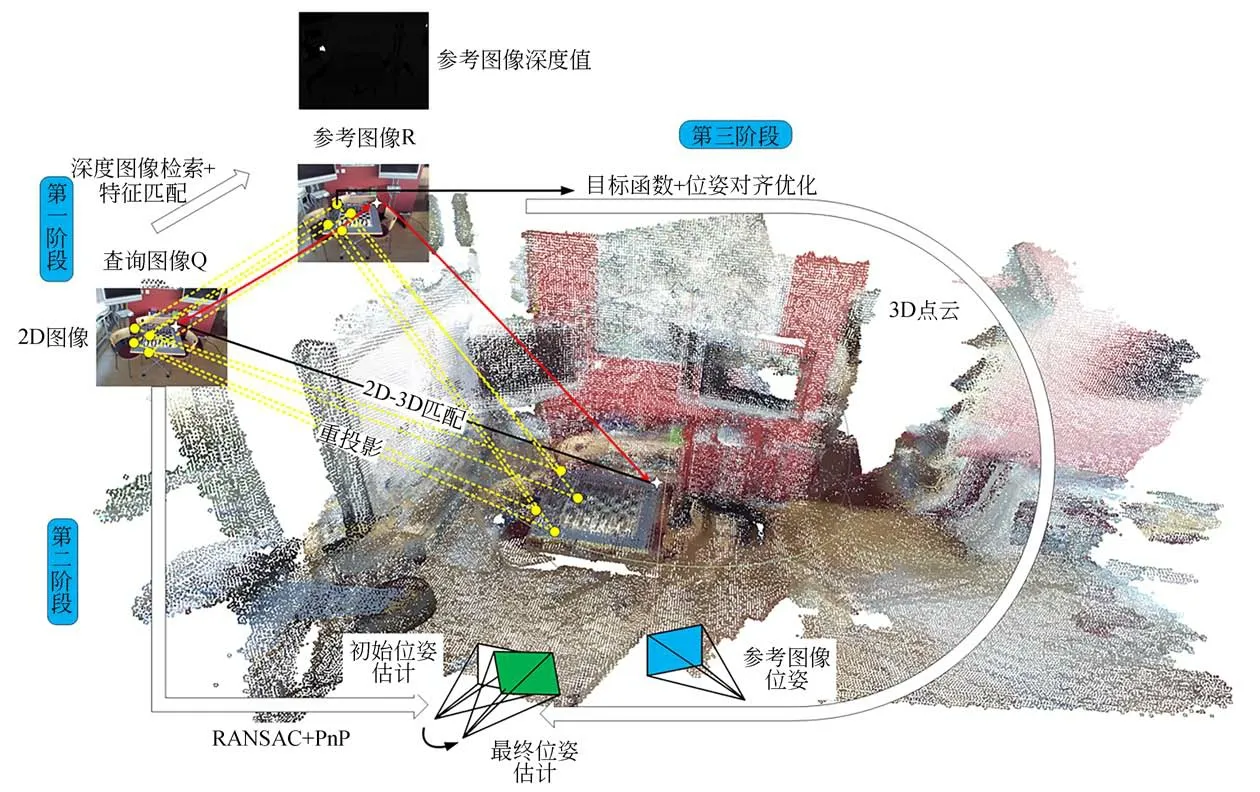
图4 多阶段相机位姿估计方法流程Fig.4 Flow of multistage camera pose estimation

3.1 构建2D-3D匹配点

为检索得到查询图像的最近邻图像（与查询图像真实位姿最接近的图像），本文采用卷积神经网络对查询图像以及已知位姿图像数据库的全局特征进行提取。采用VGG网络结构进行卷积神经网络的搭建，为了使得深度图像检索算法能够适应大部分的图像场景，将VGG网络在ImageNet数据集上进行预训练，通过一个全连接层对图像数据库以及查询图像的每一张图像提取出一个1×512的图像全局特征向量。在图像检索阶段，将图像数据库中与查询图像相似度最高的图像作为参考图像。

完成最近邻帧检索之后，对查询图像及参考图像进行特征匹配以进一步找到2D-3D匹配点。为了进一步分析不同特征描述子对特征匹配结果及最终的位姿解算结果的影响，本文分别采用ORB（Oriented Fast and Rotated Brief）算 子、SIFT（Scale Invariant Feature Transform）算子以及SURF（Speeded-Up Robust Features）算 子［11］对图像的特征进行提取，并使用暴力匹配法进行匹配。

3.2 粗位姿求解并剔除外点

使用特征匹配算法对查询图像及参考图像的特征点进行匹配，并计算像素和世界坐标间的坐标映射关系获得2D-3D匹配点，利用PnP算法对2D-3D匹配点进行位姿解算得到当前相机具体位姿。然而实际上特征匹配算法的匹配结果中可能存在误匹配点，导致最终使用PnP算法进行位姿求解时的结果误差较大，为了进一步剔除误 匹 配 点，本 文 采 用RANSAC算 法［1-3，13］的思 想对相机位姿估算的结果进行进一步的优化。图5是采用RANSAC算法思想进行位姿估计结果优化的流程图。

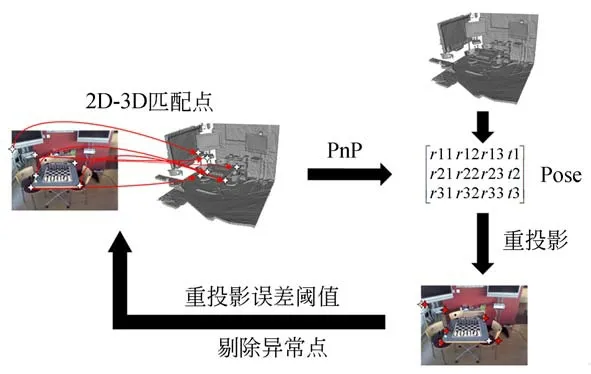
图5 RANSAC算法流程Fig.5 Flow of RANSAC algorithm

模型估计：在特征匹配算法得到的2D-3D特征匹配点中选取一定数量的点对作为PnP求解问题的输入，并采用PnP求解算法解得相机位姿假设。

模型评价：为了判断样本数据点是样本内点还是样本外点，定义重投影误差作为判断依据，重投影误差的定义如式（2）：

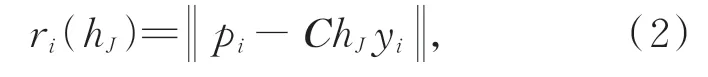
式中：pi为查询二维图像中第i个像素在图像中的2D位置，C为相机的内参矩阵，hJ为相机位姿假设数学模型，yi为pi对应的三维场景坐标真实值。由此，设置误差阈值τ，本文实验中τ=5，如果ei＜τ，则称对应点对pi-yi为内点；反之，对应点pi-yi为外点。记录每个数学模型的内点数量作为模型的评分s(hJ)。

模型筛选：重复以上步骤直至抵达迭代次数（本文实验设置为10 000次）上限或所有匹配点的重投影误差均小于预设阈值。统计不同的位姿假设数学模型下的样本内点数量，样本内点数量最多，即模型的评分最大的模型作为最佳数学模型，保留所有样本内点，剔除样本外点，并将剔除外点后的对应点对用于下一步的点云配准操作。

3.3 位姿对齐优化

位姿优化的目标是寻找最优的相机估计位姿(R̂，T̂)，使得估计的位姿矩阵与真实位姿矩阵的误差达到最小。光束平差法（Bundle Adjustment，BA）是相机位姿优化领域的一个经典方法，该方法在大量文献［11-16］中的应用也已证明其位姿优化的有效性。因此本文参考文献［16］的优化目标函数，设计目标函数构建一个光束平差问题来优化第二阶段中相机位姿估计结果，使得三维点云对于查询图像q与参考图像r的重投影差异最小化，定义的目标函数如式（3）所示：

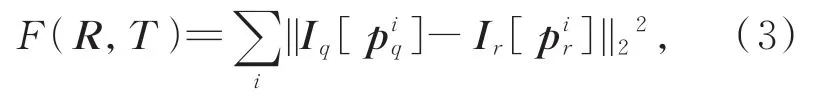
式中：piq=ChJ yi为参考图像r视场范围内的第i个3D点yi在当前相机位姿估计下的重投影坐标值，[⋅]为亚像素级别插值，本文实验过程中采用线性插值，Iq为当前像素点的归一化像素值。在欧式群SE（3）中，采用对应的李代数对位姿更新δ∈R6进行参数化［13］。本文采用高斯牛顿法来解决上述最小二乘问题，雅克比矩阵和黑塞矩阵计算如式（4）所示：

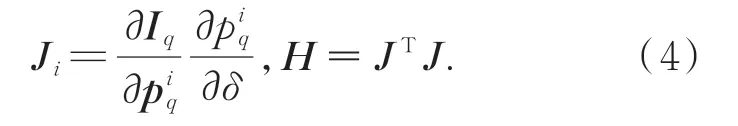
通过雅克比矩阵和黑塞矩阵计算位姿更新：

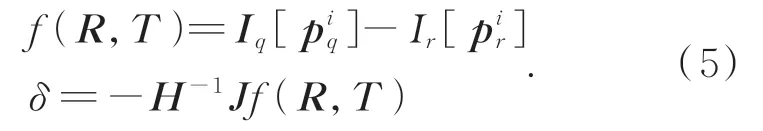
则最终的位姿更新为：

采用上述过程对估计的相机位姿(̂)进行更新，直到位姿更新量δ足够小时停止更新，本文 实 验 中 当dT＜0.005，dR＜0.05时 停 止更新。

4 基于稠密场景回归的多阶段相机位姿估计

4.1 稠密场景回归

第3节中所述采用深度图像检索及特征匹配算法来确定2D-3D匹配点，进一步实现相机的空间位姿估计。然而当图像中特征点不易提取以及查询图像与参考图像场景变化较大的情况下，该方法存在大量的误匹配点，导致最终的位姿解算结果误差较大甚至出现错误。同时由于特征匹配点较少，当存在大量误匹配点时，通过RANSAC算法剔除了异常点［17］，便无法得到足量用于PnP解算的2D-3D匹配点。然而特征点在每一帧图像像素点中占比其实是较少的，即提取的特征点相对与图像像素点来说是稀疏的，获得的2D-3D匹配点也是稀疏的。为了获得稠密的2D-3D匹配点，以此来提高相机空间位姿估计的精度，本文采用卷积神经网络对输入的RGB图像进行场景坐标回归，构建稠密的2D-3D匹配点，以实现第3节所述多阶段相机位姿估计方法中的第一阶段2D-3D匹配点的构建，提出基于稠密场景回归的多阶段相机位姿估计方法。

本文采用ResNet神经网络结构，在保证网络深度的同时防止网络的退化。为实现相机稠密坐标回归并减少计算量，对ResNet网络结构进行改进，将全连接层删除，构建全卷积神经网络，通过卷积层输出一个3通道的特征图作为最终的预测结果，网络输出为160×120的三维场景坐标回归，即是输入图像下采样后的三维场景坐标。图6是本文构建的稠密场景回归网络结构。

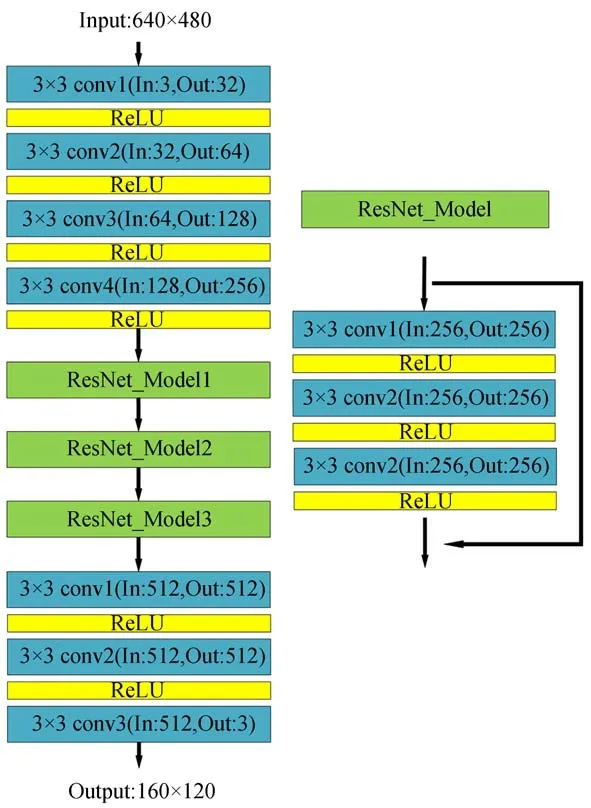
图6 稠密场景回归网络结构Fig.6 Structure dense scene regression network

采用以上神经网络结构对查询图像的三维坐标值进行回归，首先通过4个卷积层对图像的特征进行提取，之后经过3个残差网络结构对场景回归进行更好地拟合，通过卷积层输出最终的三维坐标预测值。本文的Loss函数定义如公式（7）［18］：

式中：gt_coords表示查询图像每一个像素区域对应的三维坐标真实值，pred_coords表示网络模型对查询图像每一个像素区域（4×4像素点区域）三维坐标的预测值，Norm(·)为归一化函数，s为损失因子，i表示第i个像素区域，n为像素区域总数。

4.2 场景回归结果

本文采用训练完成后的网络对数据集下的测试图像进行场景回归。本文将真实场景坐标以及预测的场景坐标的三维信息（x，y，z）映射到图像的RGB三通道，以RGB图像进行展示，各数据集下回归的结果如图7所示。

图7 各场景下场景回归的结果Fig.7 Result of scene regression

由场景回归的结果可以看出，采用神经网络对图像的三维坐标进行回归结果边缘信息丢失较为严重，这是由于本文为了减少后续位姿求解过程的计算量，将图像划分成像素区域，对每一个像素区域的三维坐标真实值进行回归，即是原始图像三维坐标下采样后的结果，因此丢失了大部分边缘信息；而对于其余部分，在本文实验的大部分场景下，图像的三维坐标预测值和三维坐标真实值基本一致。

采用卷积神经网络对图像中的像素点进行三维坐标回归也可能存在一定错误，因此在回归得到查询图像场景坐标的基础上，本文采用随机抽样的方式，随机抽取回归结果中一定数量的场景坐标预测值作为PnP求解过程的输入，解得一组相机的位姿假设hi。重复以上步骤构造n组位姿假设集合（本文实验过程中n=64），通过第三节中的RANSAC算法思路对位姿假设进行筛选，同时采用位姿对齐对估计位姿进行优化，得到最终的相机位姿估计结果。

5 位姿估计实验结果

5.1 实验环境

本文在公开数据集7scenes［14］以及自建数据集Labcore下对网络参数进行训练，其中7scenes数据集涵盖了7种不同的室内场景，是用于相机位姿估计的一个标准数据集。实验选取的硬件工作平台为台式计算机，配有NVIDIA3090显卡一张，网络模型通过PyTorch平台搭建。

5.2 位姿估计精度定量分析

相机位姿估计结果的精度可用位姿估计误差低于误差阈值（同时满足平移误差阈值和旋转误差阈值）帧数所占总帧数的百分比以及位姿估计误差中值来进行评价［15-16，19-20］。首先利用随 着误差阈值增大时，位姿估计误差低于误差阈值数所占测试集总数的百分比来衡量相机位姿估计的准确性。图8为本文所提方法在自建数据集Labcore以及公开数据集7scenes上实验的相机位姿估计准确率结果。从图中可以看出，采用多阶段相机位姿估计方法的过程中，对于大部分场景，使用SIFT算子以及SURF算子作为特征点提取时位姿估计准确率较高，在位姿估计误差阈值为5 cm/5°的范围内，自建数据集Labcore上的估计精度最大为87.3%，公开数据集7scenes上，数据集中环境变化较大时其表现较差（后3个场景）；同时，将稠密场景回归网络引入多阶段相机位姿估计方法，以此构建更为稠密的2D-3D匹配点之后，不论在自建数据集还是在公开数据集上相机位姿估计的精度均有大幅度提升。

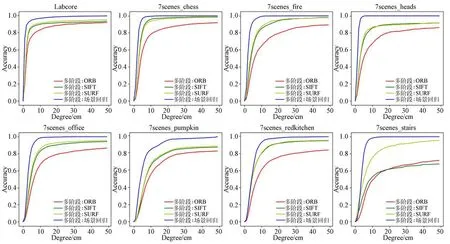
图8 位姿估计精度随误差阈值变化Fig.8 Accuracy of pose estimation varies with the error threshold

图9为引入稠密场景回归后多阶段相机位姿估计方法与其他方法在公开数据集以及自建数据集上的位姿估计准确率对比（误差阈值范围为5 cm/5°，7Scenes下为7个场景的平均准确率，Labcore下为单个场景准确率）。可以看到在公开数据集下，本文方法的位姿估计准确率为82.7%，优于DSM［9］，DSAC［12］，DSAC++［15］，SANet［20］，Pixloc［16］，同时本文将现存几种位姿估计较为优越的方法在自建数据集上进行估计，结果表明本文方法能达到94.8%的位姿估计准确率，较其余方法更加优越。其中DSAC++在自建数据集上表现相对较差，这是由于自建数据集环境变化较大，该网络无法完全拟合数据集中的场景。

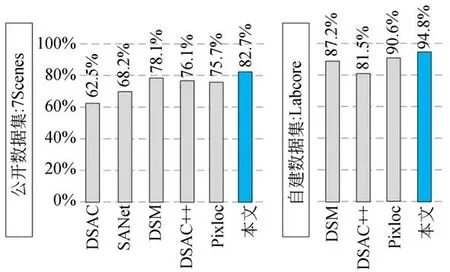
图9 位姿估计准确率对比（5 cm/5°）Fig.9 Pose estimation accuracy comparison（5 cm/5°）

其次用平移误差和旋转误差中值来衡量相机位姿估计算法的精度。图10是本文方法在自建数据集Labcore以及7scenes数据集上进行位姿估计后的估计误差中值结果。从图中可以看出，对于大部分场景，本文方法的位姿估计误差中值小于5 cm/5°。为了验证本文提出方法的精度，根据平移误差和旋转误差中值来与其他相机位姿估计方法相比较，表2为本文方法以及其他相机位姿估计方法的相机位姿估计精度，表格中的数据均来自于原始论文，加粗部分为取得各对比算法中最优的结果。从表2可以看出，采用相机位姿估计的误差中值作为评价标准时，相较于其余相机位姿估计方法，本文方法在大部分场景中位姿估计精度均有所提升。

图10 各场景下的中值误差结果Fig.10 Results of median localization Errors

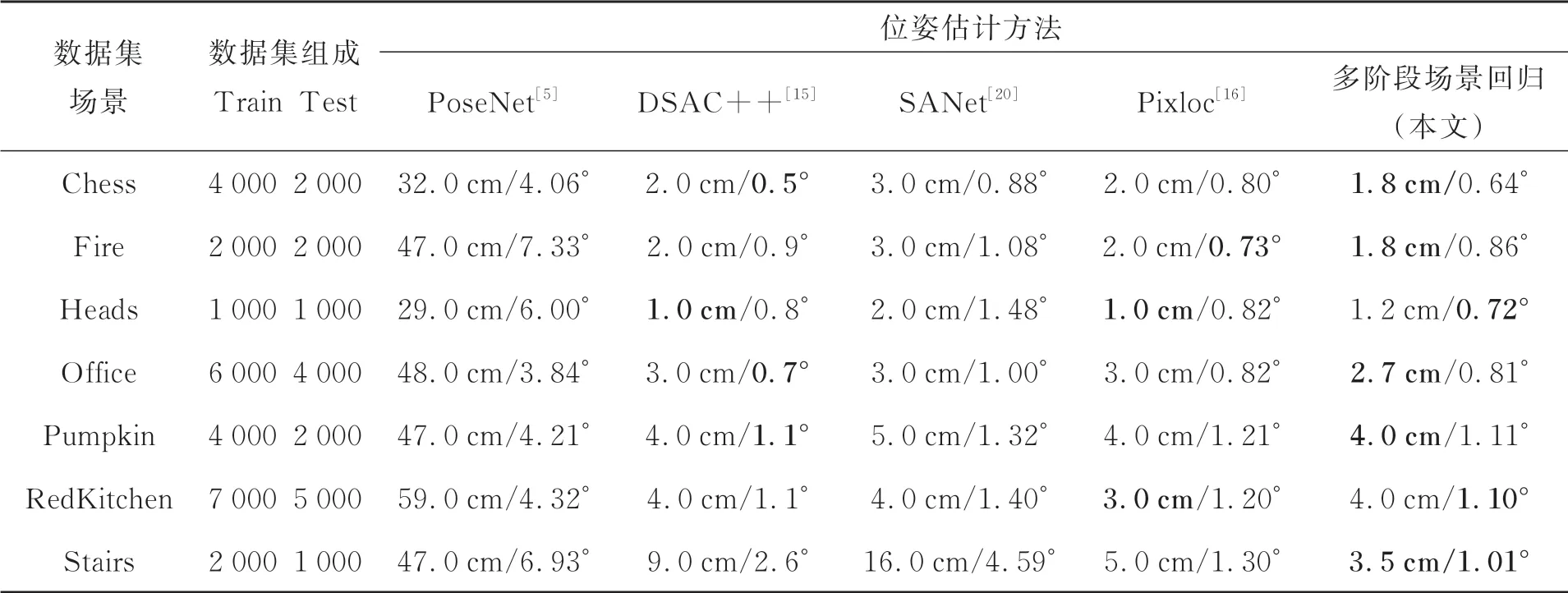
表2 相机位姿估计算法性能对比Tab.2 Performance comparison of camera pose estimation algorithms

5.3 位姿估计时耗定量分析

为对本文方法进行位姿估计的实时性进行评估，本文实验中在7scenes数据集上17 000张用于测试的场景图像进行位姿估计，并取位姿估计耗时均值作为评价指标。表3列出了本文方法与DSM［9］，DSAC++［15］，Pixloc［16］对单帧场景图像进行位姿估计时每个步骤的耗时均值，实验环境均为5.1节中所述。

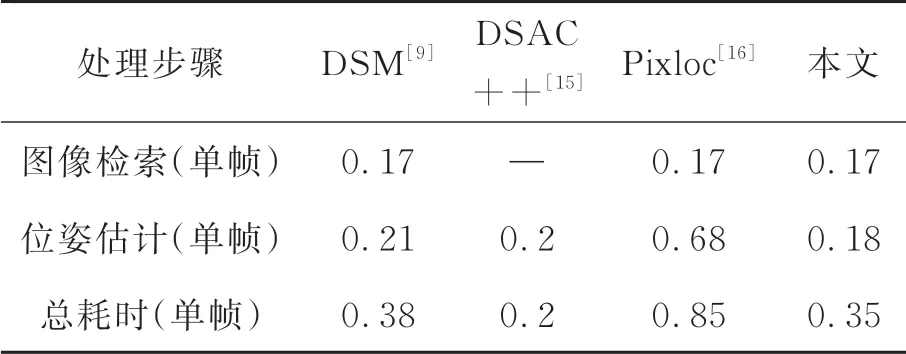
表3 相机位姿估计算法时耗对比Tab.3 Time consumption comparison of camera pose estimation algorithms （s）

6 结论

本文通过单目相机采集的RGB数据及先验的三维点云信息，实现相机位姿估计。首先根据深度图像及SFM算法，构建稠密的相机位姿估计数据集。然后将深度检索算法与基于结构的算法相结合，提出多阶段相机位姿估计方法。最后，采用全卷积神经网络回归图像的稠密场景信息，提出基于稠密场景回归的多阶段相机位姿估计算法。

实验结果证明：

1.在自建数据集Labcore下，多阶段相机位姿估计方法位姿估计中值误差为平移误差1.5 cm、旋转误差0.70°，且位姿估计准确率为87.3%（误差阈值为5 cm/5°时）；基于稠密场景回归的多阶段相机位姿估计算法位姿估计中值误差为平移误差0.3 cm、旋转误差0.60°，位姿估计准确率为94.8%（误差阈值为5 cm/5°时）。

2.在公开数据集7Scenes下，多阶段相机位姿估计的中值误差受场景变化影响较大，引入稠密场景回归后，位姿估计的精度大幅度提高，7个公开场景下的中值误差均小于5 cm/5°，同时平均位姿估计准确率为82.7%（误差阈值为5 cm/5°时）。相比于目前的相机位姿估计算法，本文算法在位姿估计环节耗时更短；在位姿估计精度上，不论从位姿估计准确率还是中值误差角度进行评价，本文所提算法均有显著的性能提升。由于本文在图像检索以及场景回归阶段均采用了卷积神经网络模型，因此在位姿估计的总时耗上相对较长。后续工作将进一步考虑实际应用的具体需求，通过简化网络模型的复杂度，提升本文位姿估计方法的效率。

从表3可以看出，本文在单帧场景图像位姿估计的计算阶段耗时为0.18 s，相比于其他3种方法来说耗时较短；同时，相比其余存在图像检索的相机位姿估计算法，本文方法相机位姿估计的总耗时最短。然而相比于文献［15］中的DSAC++，由于本文增加了图像检索阶段，因此相机位姿估计总耗时更长。本文方法耗时主要源于在图像检索以及位姿估计阶段均使用了卷积神经网络，复杂的网络结构造成了大量耗时。因此在后续工作中，综合实际应用场景的精度及时耗需求，通过简化图像检索以及场景回归阶段的网络模型，可提升本文位姿估计方法的效率。