3D位姿估计结合阻抗控制的沉孔装配

陈平，雷学军，李灿，胡义亮，陈爽

（重庆大学 机械与运载工程学院，重庆 400044）

1 引言

随着工业4.0时代的到来，智能化装配受到广泛的关注，吸引着大量的研究人员。其中装配领域最为常见的便是轴与孔的装配。随着技术的发展，轴孔装配的自动化程度越来越高，但传统的自动化装配无法满足日益智能化、精密化的装配要求，尤其是在军工、光学产品装配中。圆轴与沉孔是比较常见的配合零件，圆轴与沉孔零件的装配面临的关键问题是：（1）如何估计沉孔零件的任意的空间位置和姿态；（2）如何将轴零件柔顺地导入沉孔零件内。

关于孔零件的位姿（位置和姿态）估计方法，根据不同的相机配置和视觉技术，大致可以分为3种：采用单目相机［1-2］，采用双目相机［3-6］及采用3D相机［7-9］。胡瑞钦等人［1］建立了单目相机与探针、销钉结合的方式，利用单目相机将部件引导至辅助销钉的导向范围内以完成装配。该策略易于系统工程化，但是孔位测量匹配误差达到了2.9 mm，无法满足更精密的装配要求，此外，单目相机获取的图像丢失深度信息且易受光照影响，无法直接用于位姿估计，需要利用销钉导向，通用性不高。Zheng等人［6］采用双目相机拍摄空间中的圆孔，根据两个视角中椭圆与圆孔的几何关系，完成圆孔的空间位姿估计，但其前提是已知空间圆的半径。Shah等人［9］利用CAD创建零件的标准化模型点云，再通过3D相机获得零件的真实点云，将二者配准获得零件的空间位姿，但是该方法需要预先已知待装配零件的尺寸。Vosselman等 人［10］使用霍夫圆 柱 拟 合对圆柱点云拟合来估计其位姿。Forsman等人［11］则采用随机采样一致性（Random Sample Consensus，RANSAC）圆柱拟合来估计姿态。这些方法的前提是必须获得零件的径向点云（即侧面点云）。在沉孔的装配场景中，孔作为零件的一部分，外圆柱面形状未知，径向点云很难获取，故无法采用圆柱拟合的方法估计位姿。沉孔的上端面特征较为固定，一般由平面和平面上的圆组成，且点云数据易获得，故本文基于沉孔端面点云（轴向点云）来估计沉孔零件位姿。

零件柔顺装配的关键在于机器人的柔顺控制，已有的方法包括阻抗控制［12-15］和力/位混合控制［16］等。力/位混合控制利用接触力和位置的正交原理同时实现机器人末端的接触力和位置跟踪控制。阻抗控制通过建立机器人末端作用力与位置偏差之间的动态关系，间接地控制机器人与待装配零件之间的接触力，使机器人在受约束方向保持期望的接触力。在轴与沉孔装配过程中已完成对沉孔零件的精确定位，但由于机器人在运动过程中的位置控制误差无法完全消除，且沉孔与轴之间的配合间隙很小，很容易产生卡阻现象，此时阻抗控制便能很好地消除卡阻，实现柔顺装配。

本文针对长圆轴与沉孔的自动装配问题，通过3D相机获得沉孔的轴向点云，并针对轴向点云提出了沉孔空间位姿估计算法，同时融合阻抗控制的优点，形成3D视觉和力觉的柔顺装配策略，实现圆轴与沉孔零件的柔顺装配，可提升装配精度和装配效率，适应性更广，并满足稳定可靠的要求。

2 系统组成及工作原理

2.1 自动装配系统的硬件构成

图1展示了机器人零件装配平台的组成。其中，六自由度机器人是整个系统的载体，3D相机和单目相机安装于机器人末端法兰盘，它们共同组成整个系统的视觉部分，可实现在抓取过程中对轴的识别、定位以及装配过程中对沉孔的空间位姿估计。六维力传感器安装于机器人末端法兰盘与末端执行气爪之间，可实时监测装配过程中的力/力矩变化，从而引导机器人的移动，达到柔顺装配的目的。

待装配的零件为圆轴与沉孔零件，其基本尺寸如图1所示，沉孔零件的内径为20 mm，整个沉孔的深度为270 mm，轴零件的直径为19 mm，轴的长度为270 mm，轴孔之间的配合间隙为0.5 mm±0.05 mm。

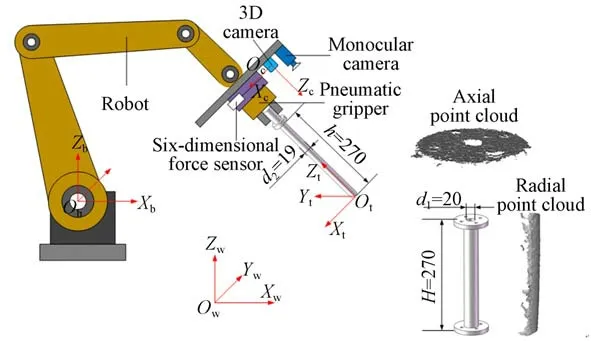
图1 机器人零件装配平台Fig.1 Platform of robotic assembly

2.2 自动装配系统的工作原理

应用该系统进行圆轴与沉孔装配的主要步骤如下：

（1）机器人移动至待装配圆轴零件工作台上方，利用单目相机，通过基于深度学习的目标检测方法完成对轴零件的识别与定位，最后完成抓取；

（2）完成抓取后，机器人移动至沉孔零件工作台上方，使用3D相机完成对沉孔零件上端面点云数据的获取；

（3）通过沉孔位姿估计关键算法获取沉孔零件的空间位姿；

（4）最后根据（3）中获取的位姿，通过阻抗控制将轴柔顺的装入沉孔中。

本文将使用预训练的网络YOLOv3来完成步骤（1）中对圆轴零件进行检测的任务，因为YOLOv3已经有较成熟的应用技术，在本文中将不再进行叙述。本文聚焦于步骤（3）和（4）的叙述，即沉孔位姿估计算法和阻抗控制。

3 沉孔位姿估计关键算法

沉孔的空间位姿可表示为(X，n)，其中X表示沉孔上端面的圆孔圆心，n表示沉孔上端面平面法线。当获得沉孔上端面点云之后，通过预处理去除点云数据中的离群点和噪声。对沉孔上端面的平面拟合可获得其平面参数，进而获得n。而X可利用沉孔轮廓的圆拟合来估计。

3.1 点云数据预处理

3D相机获得的沉孔上端面点云数据如图2所 示，表 示 为 点 集P={p1，p2，...，pn}，pi∈R3，受外部环境及相机自身噪声的影响，获得的点云存在许多离群点和噪声，这些数据影响装配位姿估计的精度，本文采取超体素聚类分割［17-18］和约束平面分割（Constrained Planar Cuts，CPC）超体素聚合［19］来去除噪声和离群点。

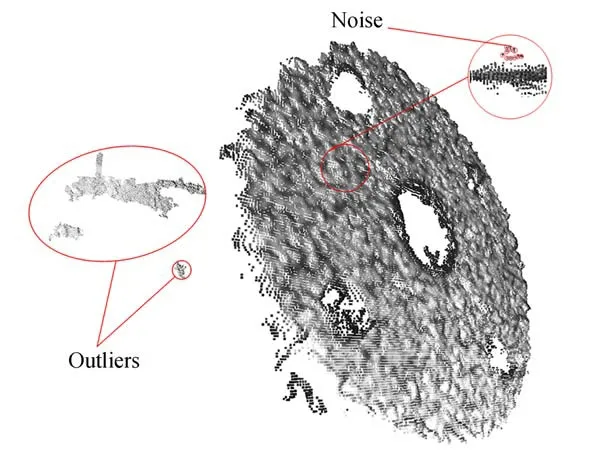
图2 点云离群点和噪声Fig.2 Outliers and noise of point cloud

超体素分割算法首先对点云数据进行体素化处理得到体素云，并且在体素空间下利用网格化来筛选出种子体素，为后续的聚类算法进行初始化。然后利用体素数据的空间位置和特征属性，设计邻接体素之间的距离度量。并利用基于流约束的聚类算法将体素云过分割得到超体素。最后由CPC聚类算法完成对离群点和噪声的去除，获得最终点云Pc={pc1，pc2，...pcnc}，pci∈R3。图3中使用不同的颜色标注出分割的超体素（彩图见期刊电子版），并连接相邻的超体素，随着体素半径和网格半径的增大，所分割的超体素个数也在增多，CPC聚类结果中使用不同的颜色将离群点标出，当体素半径为0.3 mm，网格半径为15 mm时已经可以分割出离群点，但是同时存在误分割。图4给出了在不同的体素半径下超体素的个数及分割比，从图4中可以看出在体素半径为0.32 mm之后，点云的分割比维持在75%左右，此时可有效地去除离群点和噪声。

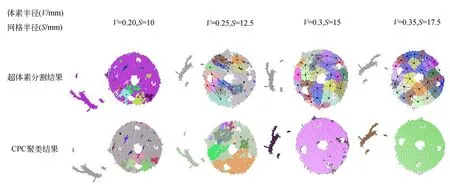
图3 超体素分割与CPC结果对比Fig.3 Results of supervoxel segmentation and CPC clustering

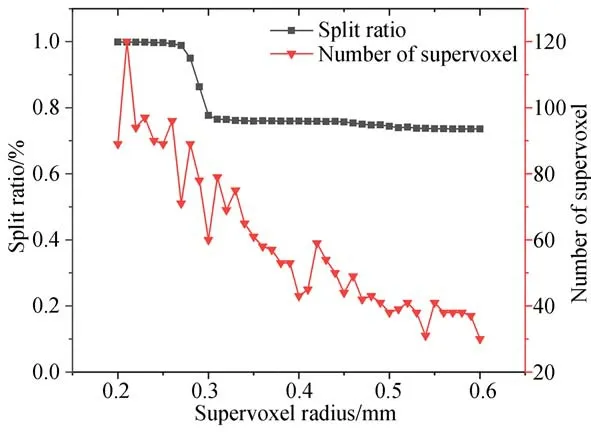
图4 超体素分割结果Fig.4 Results of supervoxel segmentation

3.2 基于权重RANSAC的沉孔上端面拟合

为获得沉孔上端面法线n，需对预处理后的点云数据进行平面拟合。预处理虽然去除了大片聚集的离群点，但是点云数据仍然存在部分分散的离群点和噪声，且在点云数据的边缘处明显增多，如图5红色标记所示（彩图见期刊电子版），这源于双目结构光相机自身的噪声和误差。针对这种点云数据，提出基于权重的RANSAC（Weight-based Random Sample Consensus，

图5 边缘离群点和噪声点Fig.5 Outliers and noise of the edge

WRANSAC）平面拟合方法来获得沉孔的上端面。因为传统RANSAC的平面拟合方法中，点云中的每个点被选中的概率是相同的，但是点云边缘点误差太大，会影响平面拟合的精度，为改进传统的RANSAC方法，对邻近沉孔中心的点赋予大权重，而远离沉孔的边缘点赋予小权重，来减小边缘点的影响，如图6所示，权重函数如式（1），式（2）所示：

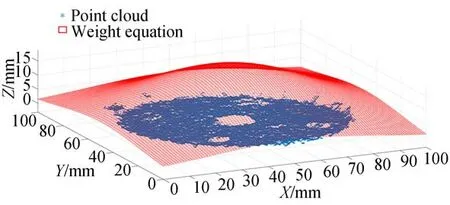
图6 权重函数示意图Fig.6 Schematic diagram of the weight function

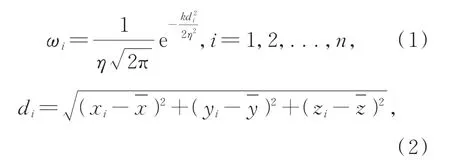
其中：di为点云中的一点pi到重心的距离，k为比例系数，η为标准差，本文取k=1/10 000，η=4。

为从拟合出的众多平面模型中筛选出最佳平面，设计如式（3）所示的评价公式：

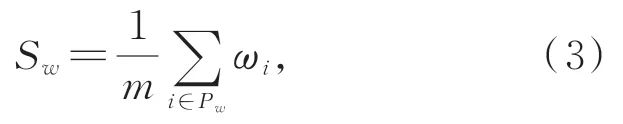
其中：Pw是与拟合平面的距离误差小于阈值β（β=0.1 mm）的点集，m是该点集的点数，归一化计算可以得到平面的尺度不变分数。

WRANSAC沉孔上端面拟合的流程如下：

（1）根据公式（1）计算点云P（c经过预处理后的点云）中每个点的概率ωi；

（2）根据每个点的概率ωi从点云Pc中选择3个点作为样本点，估计平面模型：Ai x+Bi y+Ci z+Di=0；

（3）计算点云Pc中的每个点pci与平面模型的距离，将距离小于阈值β的点记录在点集Pm（内点集）中；

（4）根 据 公 式（3）计 算 该 平 面 模 型 的得分Swi；

（5）重复步骤（2）～（4），达到最大迭代次数（本文设置的迭代次数k=100）则停止。

选取分数Sw最大的估计作为最终的平面拟合模型：Ax+By+Cz+D=0，拟合的平面如图7所示的P平面。

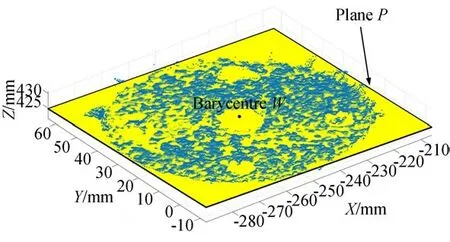
图7 平面拟合结果Fig.7 Results of plane fitting

3.3 沉孔圆拟合

经过3.2的平面拟合后，可获得沉孔上端面：Ax+By+Cz+D=0，则n=(A，B，C)。而X可通过对沉孔轮廓的圆拟合来获得。

3D相机获得的点云如图8所示（彩图见期刊电子版），沉孔轮廓并非为圆（如图中红色实线），轮廓应为图中红色虚线所示，这是因为3D相机在扫描沉孔的时候，会在沉孔圆内生成一些无关的点云数据（沉孔内点），如图8红色实线与虚线内的点，为了提取出沉孔的轮廓，完成轮廓的圆拟合，需要将沉孔内点分割出来，然后再提取出沉孔轮廓进行圆拟合，以完成对X的估计。

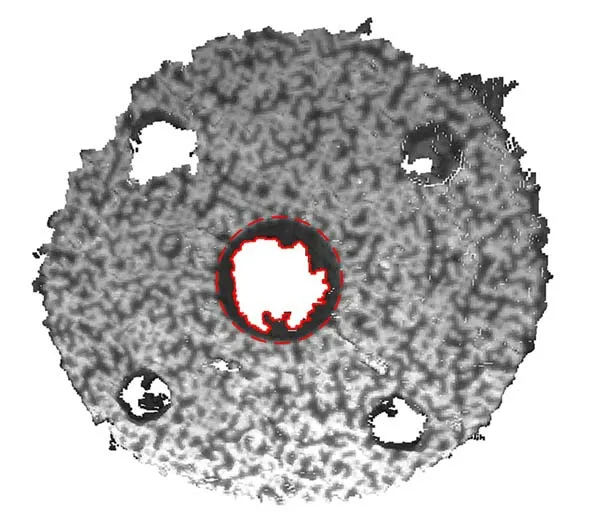
图8 点云数据Fig.8 Point cloud

点云数据在3D相机获取的过程中会根据深度不同赋予不同的RGB值。在经过沉孔轮廓时点云数据的法线方向会发生改变，属于上端面的点云法线应与端面法线方向一致，而沉孔内点的法线方向会因深度的不同发生偏移。据此，利用结合颜色和法线信息的权重函数，来完成对沉孔内点的分割。

权重函数如式（4）所示：

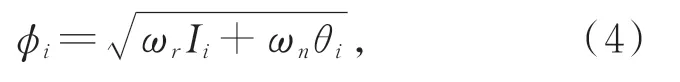
其中：Ii为 点 的RGB值，θi为点的法 线 与 上 端 面的法线n=(A，B，C)的夹角，ωr为颜色值的权重，ωn为法线夹角的权重，同时设定阈值λ，只有当φi大于阈值λ的点才会被筛选为沉孔内点，经过该权重函数的筛选之后，可完成对沉孔内点的分割，图9中红色点为利用公式（4）分割出的沉孔内点（彩图见期刊电子版），其中包含部分螺纹孔的点云和边缘点云，再次利用3.1节中介绍的超体素分割和CPC聚类分割出属于沉孔的部分，并表示为Pe={pe1，pe2，...，pen}，pei∈R3。

图9 沉孔内点Fig.9 Inliers of countersunk-hole

为完成对沉孔轮廓的圆拟合以确定上端面圆心X，将点集Pe中的点投影到3.2拟合的平面Ax+By+Cz+D=0上，提取出其外部轮廓，然后完成圆拟合，估计出圆心X。

令点集Pe中 一 点为pei(x0，y0，z0)，设其在 平面上的投影为pplane(xp，yp，zp)，则有：

将式（5），式（6）代入平面方程Ax+By+Cz+D=0，可以解得：

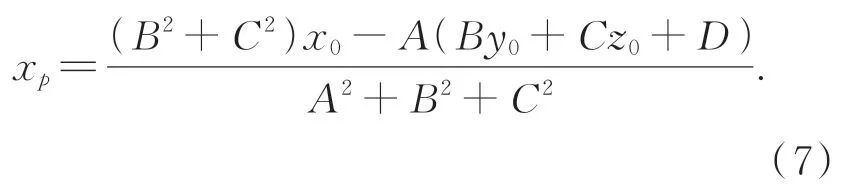
将式（7）代入式（5），式（6），可以解得：

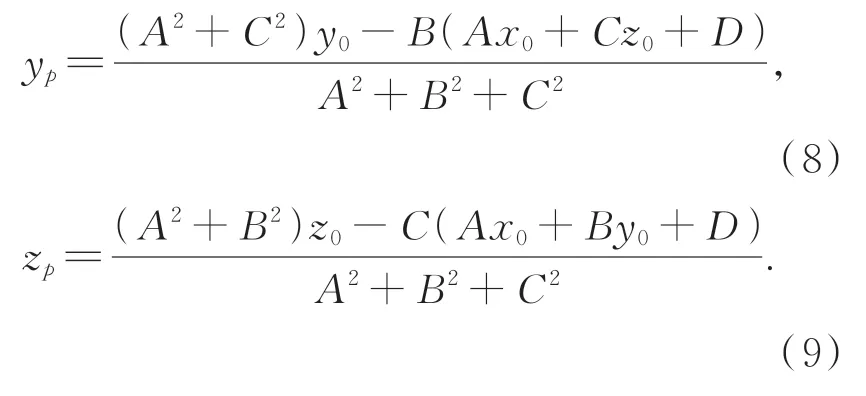
经过平面投影后，所有的沉孔内点都在平面Ax+By+Cz+D=0上，如图10所示（彩图见期刊电子版），通对这些内点的轮廓点提取获得二维点集Pcircle，如图10中红色点所示。通过对点集Pcircle的圆拟合便可估计出沉孔上端面圆心X。

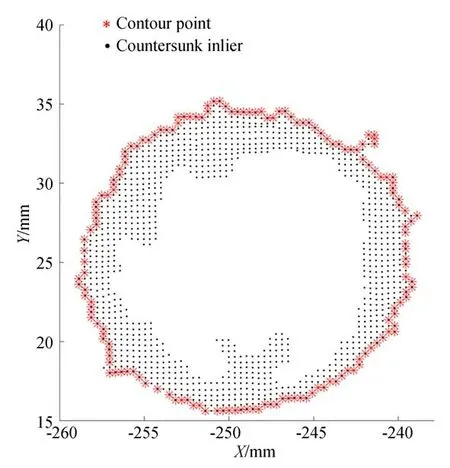
图10 沉孔轮廓Fig.10 Profile of countersunk-hole

在现有的圆拟合方 法中，Hyper算法［20-22］的精度和速度都领先于同类算法，且它可以完成对残缺的圆的拟合，故本文采用Hyper算法完成对点集Pcircle的圆拟合，首先，将圆表示为代数方程形式：

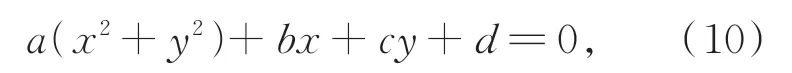
其中：a，b，c，d为圆的待求参数，将其表示为向量形式为：A(a，b，c，d)，将式（10）转换为圆参数方程的一般形式：

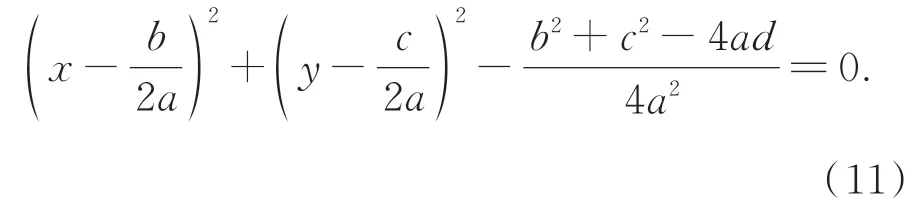
则圆心为：

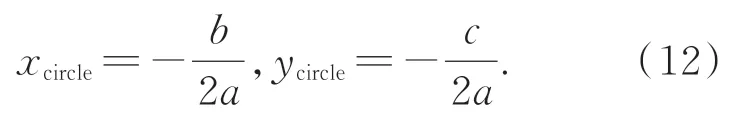
半径为：

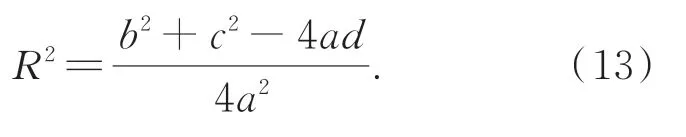
将点集Pcircle表示为矩阵形式为：

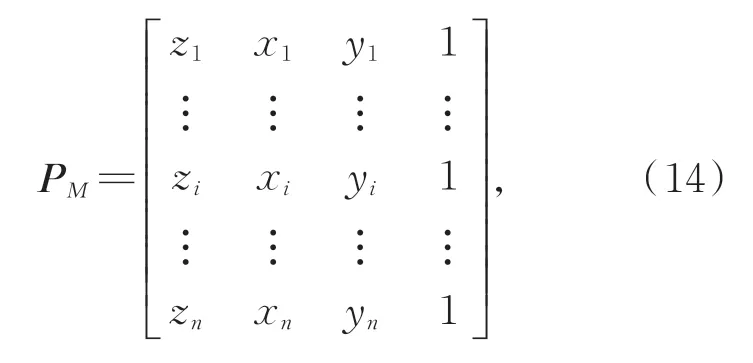
其中zi=x2i+yi2，xi，yi为点集Pcircle中点的x，y坐标。定义矩阵M为：

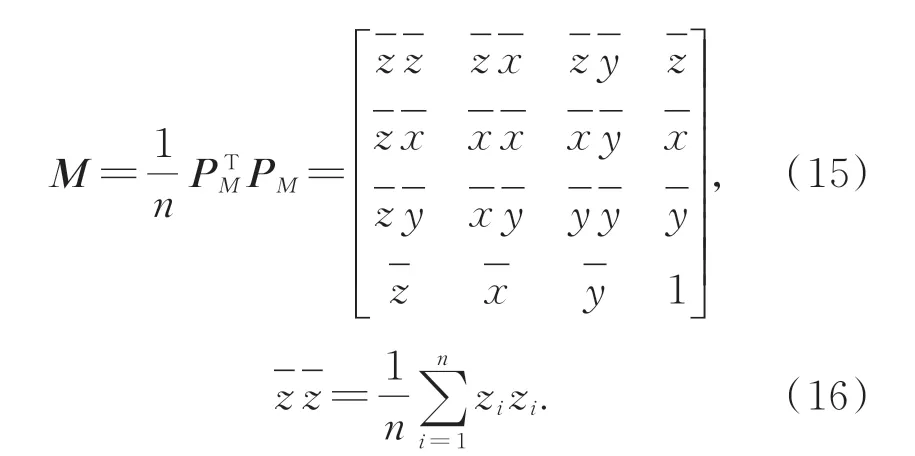
M矩阵中的求法与公式（16）中的相同。在ATNA=1的约束下，Hyper算法将圆拟合问题变成最小化函数F(A)=ATMA问题，只需要解决广义特征值问题MA=ηNA，选择所有解中最小的η和对应的单位向量作为最终拟合结果，即A等于单位向量。其中矩阵N为：

具体求解过程为对矩阵PM进行奇异值分解，PM=UΣVT，如果分解出的最小特征值σ4＜10-12，则A为矩阵V的第4列，当σ4≥10-12时，令Y=VΣVT，并求解YN-1Y的特征对，选择具有最小特征值的特征对(η，A*)，此时待拟合圆参数向量A(a，b，c，d)=Y-1A*，至此，完成对沉孔轮廓圆的拟合，将圆心点投影回三维空间便可确定X。

至此，得到了沉孔零件的空间位姿，即

(X，n)。

4 轴孔零件的阻抗控制

机器人末端气爪沿着沉孔轴线将轴零件移入孔内。然而，考虑到机器人位置控制误差、沉孔轴线位姿估计的误差，轴与沉孔配合间隙较小且轴与孔的长度较长，轴零件部分插入孔内，可能会接触沉孔零件内壁，发生卡阻现象。因此，为避免卡阻现象，在轴插入孔的过程中，采用阻抗控制［12-15］自适应地调整末端执行器的姿态，从而使轴零件柔顺地装入孔内，直至轴零件插入沉孔三分之二后，松开气爪，轴在重力的作用下完成整个装配。

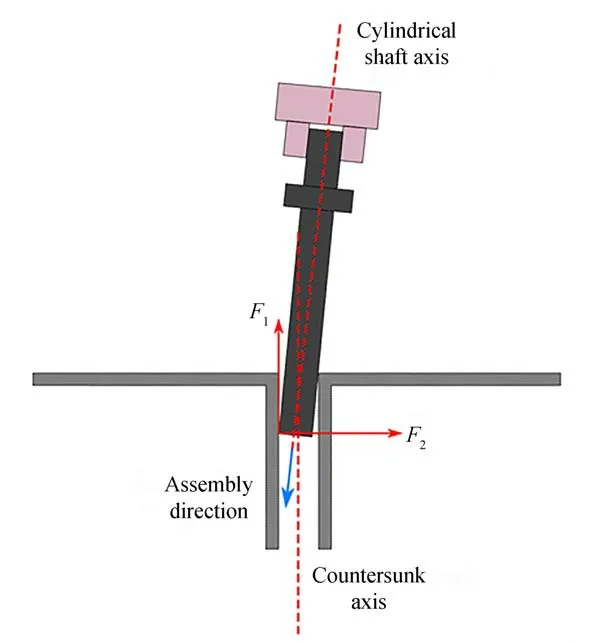
图11 圆轴零件与孔壁接触时的接触力Fig.11 Contact force generated when the cylindrical shaft part contacts the hole wall

轴零件插入沉孔的过程中，当轴与孔相互作用时，可建立二阶线性［13］方程：

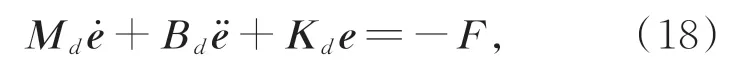
其 中：e=(ex，ey，ez)是 末 端 执 行 器 的 位 置 修 正量，F是来自环境的外力，Md，Bd，Kd分别为期望惯性矩阵、期望阻尼矩阵和期望刚度矩阵。阻抗控制过程中，根据式（18）可以根据力偏差计算位置修正量e，通过e对机器人末端执行器的姿态持续调整，以避免产生卡阻，实现柔顺装配。

5 实验与结果

5.1 实验条件

实验系统实物如图12所示。机器人末端安装单目相机、3D相机、力/力矩（F/T）传感器和气爪。机器人为安川公司的YASKAWA MOTOMAN MCL-50型机器人，有效载荷为50 kg，位置控制精度可达0.07 mm。单目相机为大恒MER-200-20G型号的工业相机，分辨率为1 268×1 236。3D相 机 型 号 为IDS Ensenso N10，其获取的点云位置精度可达到0.1 mm。六维力传感器即力/力矩（F/T）传感器，选用的型号为ATI-FT26044，其沿x轴与y轴方向的力Fx，Fy的量程为660 N，分辨率为1/8 N，沿z轴方向的力Fz的量程为1 980 N，分辨率为1/4 N；力矩Tx，Ty，Tz的 量 程 为60 N·m，分 辨 率 为10/1 333 N·m。在实验之前，已完成了单目相机和3D相机的手眼标定，六维力传感器已进行标定和重力补偿，且在轴零件末端圆心处采用五点法建立了工具坐标系。机器人已根据单目相机对轴零件的识别与粗定位完成抓取并移动到沉孔零件的上方，用3D相机拍摄沉孔零件的上端面获得点云，因3D相机已完成手眼标定，故相机坐标系下的点云可直接转换到机器人基坐标系下。

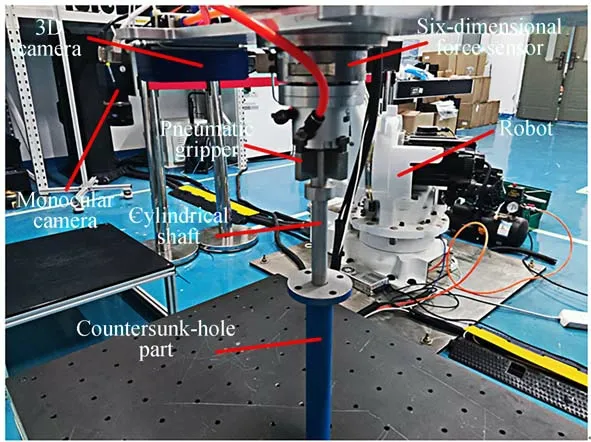
图12 沉孔零件装配平台Fig.12 Platform of countersunk-hole part assembly

5.2 基于权重RANSAC的沉孔上平面估计

为验证所提出的WRANSAC沉孔端面拟合算法在噪声和离群点的干扰下的鲁棒性，使用meshlab生成平面点云，其平面方程为z=0，即平面的参数A=0，B=0，C=-1，D=0，利用MATLAB为该点云添加零均值μ=0，标准差σ2=2的高斯噪声，分别使用M样本估计一致性［23］（M-Estimate Sample Consensus，MSAC）、最小二乘法［24］（Least Square，LS）、霍夫变换［25］（Hough Transform，HT）、随 机 采 样 一 致 性（RANSAC）与本文提出WRANSAC对生成的点云数据进行平面拟合，并计算模型内点到理想平面的平均距离Δd和拟合平面法线与理想平面法线的夹角Δθ，结果如图13和表1所示。此外为验证算法对离群点的鲁棒性，在上述点云中加入15%的离群点，实验的结果如图14和表2所示。

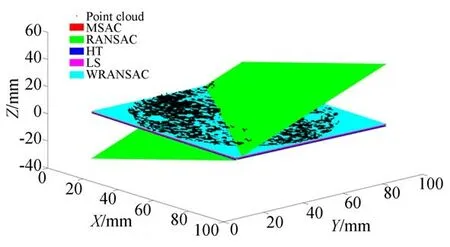
图13 平面拟合结果对比Fig.13 Comparison of plane fitting results

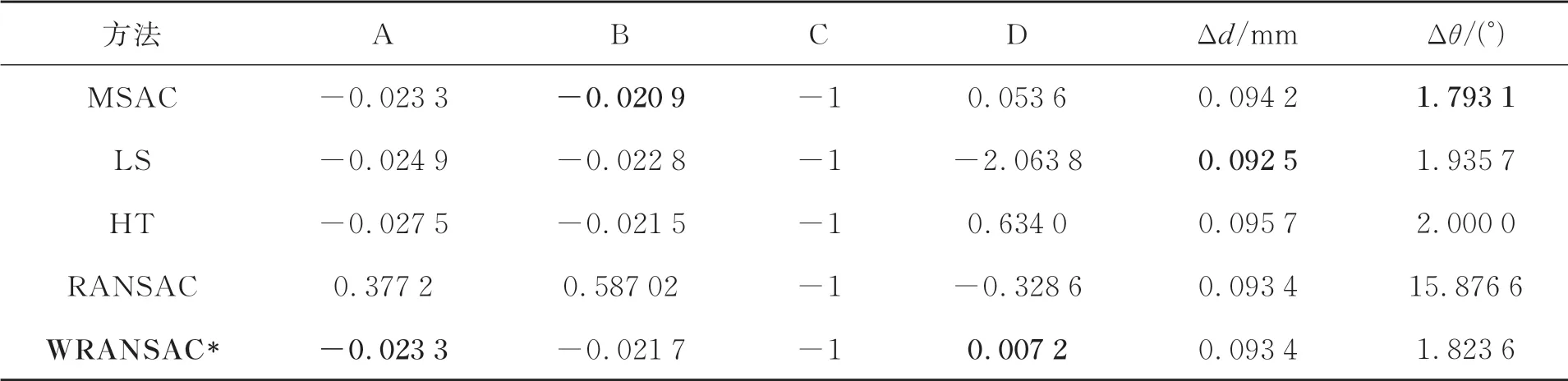
表1 平面拟合结果Tab.1 Comparison of plane fitting results

表1中，在没有离群点的干扰时，本文方法WRANSAC估计的平面参数A=-0.023 3，B=-0.021 7，D=0.007 2，角 度 误 差 达 到Δθ=1.823 6°，平均距离误差Δd=0.093 4 mm，与MSAC，HT的估计结果相差不大，优于RANSAC和LS方法，其中HT的估计结果精度虽然也很高，但是HT的计算量太大，严重影响算法的速度。表2中，在加入15%的离群点后，本文方法估计的平面参数A=-0.024 1，B=-0.022 1，D=-0.136 6，估计结果受离群点的影响很小，角度误差为Δθ=1.872 0°，平均距离误差Δd=0.092 6 mm，而其他几种方法的结果都受到一定的影响，LS和RANSAC所受影响最大，LS估计的平面模型参数B已经达到1.474 2，从图14中可以看到LS估计的平面已经严重倾斜。通过以上仿真结果，可以看出本文方法对噪声点和离群点具有良好的鲁棒性。

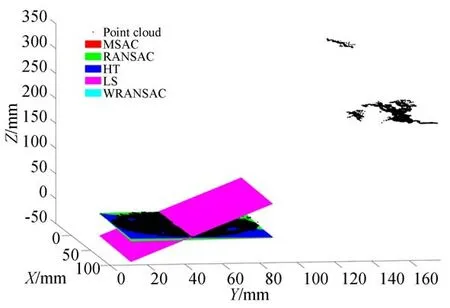
图14 离群点下平面拟合结果对比Fig.14 Comparison of plane fitting results under outliers

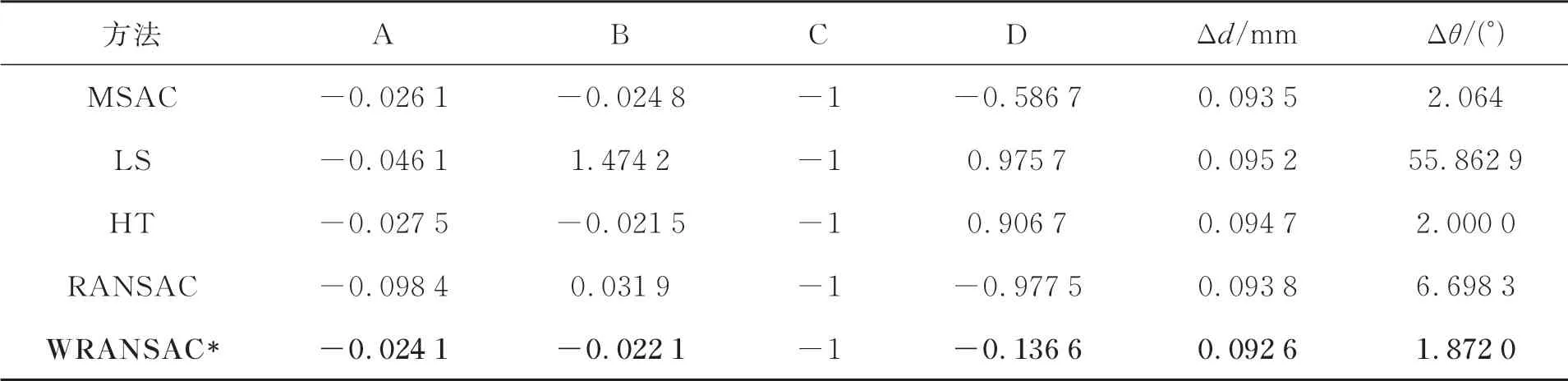
表2 离群点下平面拟合结果Tab.2 Comparison of plane fitting results under outliers

5.3 沉孔零件装配实验

使用图12所示的机器人平台，验证所提出的3D视觉引导定位和阻抗控制下的柔顺装配策略在装配中的有效性和可靠性。实验中对4种不同位姿的沉孔进行位姿估计，每一种姿态下的沉孔进行10次实验，取10次实验的平均值作为最终估计值。

在装配实验时，机器人根据单目相机对轴零件识别与粗定位后抓取并移动到沉孔零件的上方，使用3D相机对沉孔的上端面进行拍摄获得点云，并根据该点云对沉孔位姿进行估计。估计过程如图15所示（彩图见期刊电子版），沉孔位姿表示为(X，n)，①为原始点云P，②为去除部分离群点和噪声后的点云Pc，③中红色平面为WRANSAC平面拟合结果，即获得n，④为沉孔内点筛选结果，⑤为沉孔轮廓圆拟合结果，即获得X，至此完成整个沉孔的位姿(X，n)估计，将其表示成沉孔轴线与沉孔上端面的形式，如⑥所示。

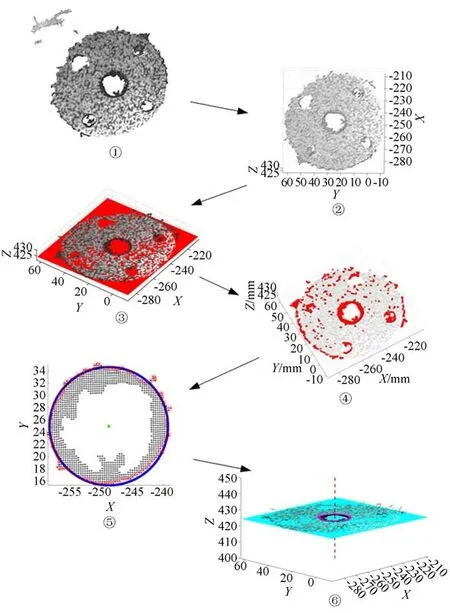
图15 沉孔位姿估计流程Fig.15 Process of countersunk hole pose estimation

由于空间中沉孔的真实姿态(X，n)无法获得，为此本文提出，在轴孔阻抗控制完成时，使用最终轴的姿态作为理想沉孔位姿(X*，n*)，来计算4种不同位姿下的位姿估计均方根误差（Root Mean Square Error，RMSE）：

图16 装配过程Fig.16 Assembly process

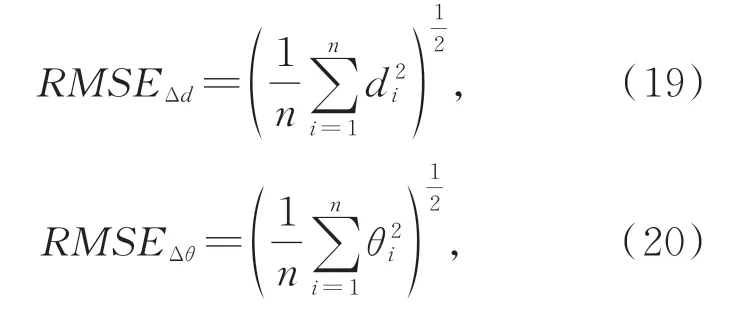
其中：θi为n与n*的角度差(°)，di为X与X*的距离差（mm），n为10，即进行了10组实验。比较结果如表3所示，可以看出，4种姿态下，本文方法估计的沉孔位姿的距离均方根误差小于0.5 mm，角度均方根误差小于0.7°，估计结果稳定。

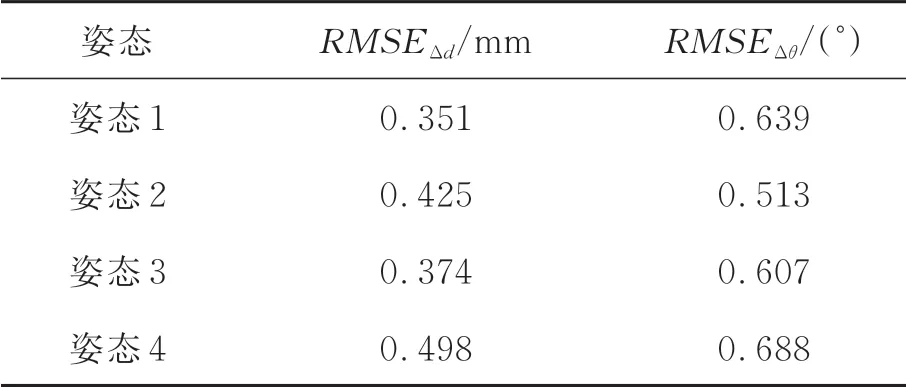
表3 不同姿态的误差结果Tab.3 Error of different postures

根据估计的沉孔位姿，进行装配，其中一次装配过程中的力与力矩的变化如图17所示，开始时刻，力与力矩几乎为零，此时力和力矩未达到触发阻抗控制的阈值，表明轴与孔无激烈的碰撞，轴可以准确平稳的装入沉孔中，也从侧面反映出本文提出的3D位姿估计算法位姿估计准确。在轴零件达到一定的深度之后，轴与沉孔内表面产生接触，导致力和力矩发生突变，当达到阈值之后，阻抗控制开始作用，机器人自适应的调整末端执行器的姿态，避免产生过大的力和力矩，从图17中可以看到，中间时刻，力和力矩突增，后在阻抗控制的调整下力和力矩逐渐减小。最后，当装配完成时，力和力矩再次接近零。其中力反馈控制中的力响应阈值为10 N，力矩响应为1 N·m。

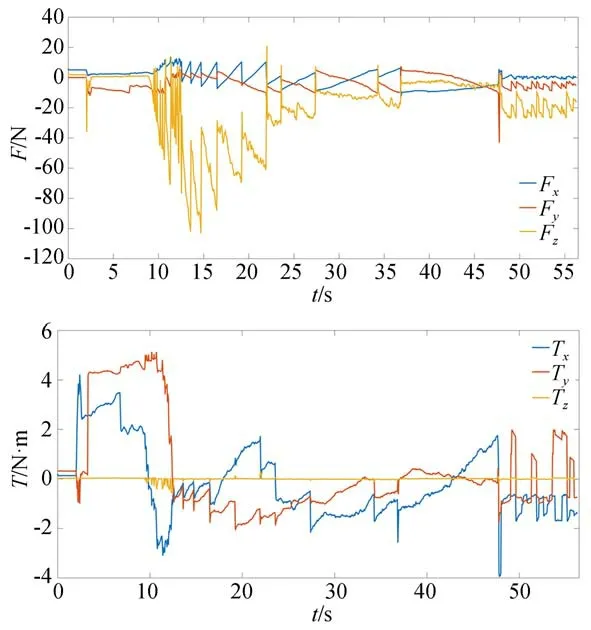
图17 力和力矩Fig.17 Force and torque

至此，整个装配过程完成。

6 结论

本文针对圆轴与沉孔的装配问题，提出了一种3D视觉引导定位和阻抗控制下的柔顺装配策略。介绍了基于WRANSAC的沉孔上端面拟合的基本原理并与经典的平面拟合方法进行了对比实验，实验表明本文方法拟合出的平面的平均距离误差Δd可以达到0.09 mm，角度误差Δθ可以达到1.8°。同时也介绍了沉孔空间位姿获取算法流程。实验表明：本文提出的算法策略可以完成配合间隙为0.5 mm的沉孔装配，满足工程实施的要求。