双余度电机两种模式下电磁力及电磁振动分析
李国栋, 郝翊帆, 马东娟
(1. 国网山西省电力公司电力科学研究院, 山西 太原 030001; 2. 中北大学 朔州校区, 山西 朔州 036000)
0 引 言
双余度永磁同步电机由于其结构简单、 效率高、 可靠性高等优点, 应用于航空航天、 军事等领域, 但其同样也存在振动和噪声问题.
电磁振动是电机振动的一个主要来源. 国内外学者对电机的电磁力及电磁振动问题进行了广泛深入的研究. 文献[1-3]针对不同槽极配合的表贴式无刷直流电机采用解析法对引起电磁振动的径向电磁力进行推导, 取得了较好效果. 文献[4-6]分析了不同槽极配合的永磁同步电机的电磁振动情况, 并针对主要的振动源, 提出了一种抑制振动的方法. 文献[7]利用等效磁路网络的方法研究了无刷直流电机内部的径向电磁力. 文献[8]以小型分数槽永磁电机为研究对象, 提出的磁固耦合方法更能精确地反映电机振动的频谱特性. 文献[9]研究了异步电动机在非正弦波供电电压下的气隙磁场引起的定子铁芯电磁振动. 文献[10]通过解析法分析了表贴式永磁同步电机定子的振动特性, 以此来降低声压等级并优化电机性能. 文献[11]以9/8和3/2两台永磁同步电机为例, 针对非对称齿槽结构永磁电机的不平衡磁拉力进行了研究. 文献[12]分析了24/22无刷电机的径向磁密和径向电磁力分布, 并进行了相关的振动实验. 文献[13]从电磁振动源的角度出发, 通过分析脉动转矩、 齿槽转矩和径向电磁力得到永磁同步电机的振动情况.
本文对一台定子采用分数槽集中绕组、 槽极数配合为12/10的各相绕组间低热耦合双余度永磁同步电动机(以下简称双余度电机)在正常运行和故障后单余度运行下电磁力引起的电磁振动进行分析. 首先对双余度电机进行二维电磁场仿真, 得到两种工况下电机内部的磁场分布情况. 然后, 对电机定子内表面的电磁力进行计算. 最后, 将所得到的电磁力耦合到电机的瞬态结构有限元模型中, 对比分析两种工况下电机定子的电磁振动.
1 双余度永磁同步电机基本结构
各相绕组间低热耦合双余度电机剖面图如图 1 所示, 其主要参数见表 1.

图 1 双余度永磁同步电动机剖面图Fig.1 Cross-sectional diagram of the DRPMSM

参数数值参数数值额定功率/kW10铁心长度/mm150额定电压/V280定子外径/mm120额定电流/A18.8定子内径/mm61额定转速/(r·min-1)3600转子外径/mm58槽数/极数12/10永磁体厚度/mm4.46~5.50定子齿高/mm22.5定子槽肩角/(°)45定子槽口宽/mm2定子磁轭高/mm6定转子叠压系数0.95极弧系数0.85
由图 1 可见, 在相邻的两相绕组之间放置隔热板, 可以使各相绕组的热耦合减弱, 这样在一相绕组由于短路故障而发热时, 并不会影响其他绕组. 6个相绕组按照A1、 B2、 C1、 A2、 B1、 C2的顺序排布, 最后连接成A1B1C1和A2B2C2的两套Y接对称绕组. 两套绕组中相同冠名相的电动势大小相同、 相位相同; 两套绕组在空间上互补交叉布置, 便于单余度运行时绕组铜耗的散热. 两套绕组由两台逆变桥供电, 正常时, 双余度运行, 两台逆变桥同时供电; 当某一套系统的绕组或逆变桥发生故障时, 进行余度切换, 单余度运行, 由另一套无故障系统供电[14].
为了使双余度电机在一套绕组故障时也能正常工作, 电机正常运行时并不是在额定负载下工作, 而是带0.7倍的额定负载. 这样可以保证电机在一套绕组故障被切以后, 另一套绕组单独工作时, 不会有由于电枢电流太大而产生发热严重的问题.
2 双余度电机定子电磁力分析
2.1 电磁力定性分析
一般永磁电机定子内表面的径向磁密远高于切向磁密, 电机的电磁振动主要是由径向电磁力产生的. 下面定性地分析电机径向磁密和径向电磁力的谐波组成[1].
电机空载时转子上永磁体产生的径向磁密为
(1)
式中:n为永磁空间谐波次数;p为电机极对数;ω为电机机械转速;r为所取气隙圆半径;θ为转子位置角;Bn(r)为气隙处的n次空间谐波磁密幅值.
电机负载时由交轴电流产生的径向磁密为
BA(r,θ,t)=

式中:l为空间谐波次数;j为电流时间谐波次数, 而且满足下式关系
l±j=3C,C=0,±1,±2;(3)
Imj为j次电流时间谐波的幅值;φj为j次电流时间谐波初相角;Bl(r)为l次空间谐波磁密幅值.
因此, 电机负载时的径向气隙磁密为
BL(r,θ,t)=BP(r,θ,t)+BA(r,θ,t).(4)
在极坐标中, 电机定子内表面的电磁力可由麦克斯韦应力张量法计算而得. 任意一点的径向电磁力密度可表示为
(5)
式中:μ0为空气磁导率.
若永磁体产生的空间谐波磁密次数为n1,n2,n3,…, 而交轴电枢反应产生的空间谐波磁密次数为l1,l2,l3,…, 由式(4)和式(5)可知电机负载下径向电磁力由以下3部分组成:
1)k=2nμ和nμ±nν(μ=ν=1,2,3,…), 只由永磁谐波磁密产生;
2)k=2lν和lμ±lν(μ=ν=1,2,3,…), 只由电枢反应谐波磁密产生;
3)k=nμ±lν(μ=ν=1,2,3,…), 由永磁谐波磁密和电枢反应谐波磁密相互作用产生.
2.2 径向磁密分析
取靠近双余度电机定子内表面的一个气隙圆路径代替定子内表面, 分别得到如图 2 所示的某一时刻双余度电机在正常运行和故障单余度运行时的气隙磁密.
由图2(a)可以看出电机在单余度运行后, 气隙径向磁密波形在一定程度上发生了变化. 这是由于电机故障绕组的电枢反应磁场消失所造成的. 由图2(b)可以看出电机在单余度运行后, 径向磁密不仅在幅值上有所差异, 同时出现了幅值比较小的偶数次谐波, 如2次和4次. 由于两种工况下永磁体是相同的, 只是电枢绕组不同, 可知差异是由电枢反应磁场造成的. 以下对两次的电枢反应磁场进行比较分析.
从图 3 可以清楚地看出两次电枢反应磁场的差异, 从图3(a)可知非故障线圈处的电枢反应磁密在单余度运行时要比电机正常工作时的大. 这是因为在单余度运行时要保证足够的输出转矩, 因此需要通更大的电枢电流, 于是形成了更强的电枢反应磁场. 从图3(b)可以看到两种工况下电枢反应磁场最大的区别不仅是幅值上的差异, 更在于谐波次数的不同. 单余度运行时使全部的偶数次谐波出现, 这是在电机正常运行时不存在的. 下面以A相绕组为例对两种工况下的电枢反应磁场进行详细分析.

图 2 两种工况下定子内表面径向磁密及其FFT分解Fig.2 Radial magnetic flux density of stator inner surface and its FFT decomposition in two conditions

图 3 两种工况下电枢产生的径向磁密及FFT分解Fig.3 Radial magnetic flux density produced by armature windings and its FFT decomposition in two conditions
正常工作时A相绕组产生的磁动势波形如图 4 所示. 对图 4 的磁动势波形进行傅氏级数分解, 由于磁势波形是关于F轴的偶函数, 于是此时的A相绕组磁动势可以表示为
(6)
式中:F1,F2,…,Fν分别为极对数为1,2,3,…,ν的谐波磁动势的幅值.Fν可由傅氏级数积分求得

式中:i为电枢电流;Nc为A相绕组一个线圈的串联匝数.

图 4 双余度永磁同步电机正常运行时A相绕组电流产生的磁动势波形Fig.4 A phase MMF when DRPMSM working normally
可以看出, 当ν为偶数时, A相绕组产生的磁动势Fν为0. 只有极对数为奇数的磁动势谐波才存在. 当三相绕组星形连接后, 就消除了极对数为3的倍数的磁动势谐波, 于是最后就只存在极对数为1,5,7,11,….
双余度电机故障后, 单余度运行时A相绕组产生的磁动势波形如图 5 所示.

图 5 双余度永磁同步电机单余度运行时A相绕组电流产生的磁动势波形Fig.5 A phase MMF when DRPMSM working in one
同样对图 5 的磁动势波形进行傅氏级数分解, 由于此时的磁势波形是关于F轴的奇函数, 于是A相绕组磁动势可以表示为
F(α)=F1sinα+F2sin2α+F3sin3α+…+

同样对Fν用傅氏级数积分求得, 此时表达式为

此时, 无论ν为奇数还是偶数, A相绕组产生的磁动势Fν都不为0, 也就是所有极对数的磁动势谐波都存在. 当三相绕组星形连接后, 同样消除了极对数为3的倍数的磁动势谐波, 于是最后的磁动势谐波极对数为1,2,4,5,7,8,….
2.3 径向电磁力分析
当所取气隙圆半径一定时, 由于BL不仅是空间的函数波, 也是时间的函数波, 根据式(4)可知, 电磁力也是空间和时间的函数波. 对该电磁力进行FFT分析, 从而得到电磁力在空间和时间上的表达式为[4]
(10)
式中:F0为电磁力的恒定分量;Fυk为各阶谐波电磁力幅值;υp为径向力在时域上的变化频率;k为空间谐波次数;kp为径向力的模数;θ0为转子的初始位置角.
通过仿真计算可以得到双余度电机在正常运行和故障单余度运行时, 定子内表面径向电磁力随转子位置的关系及其FFT分解如图 6 所示.
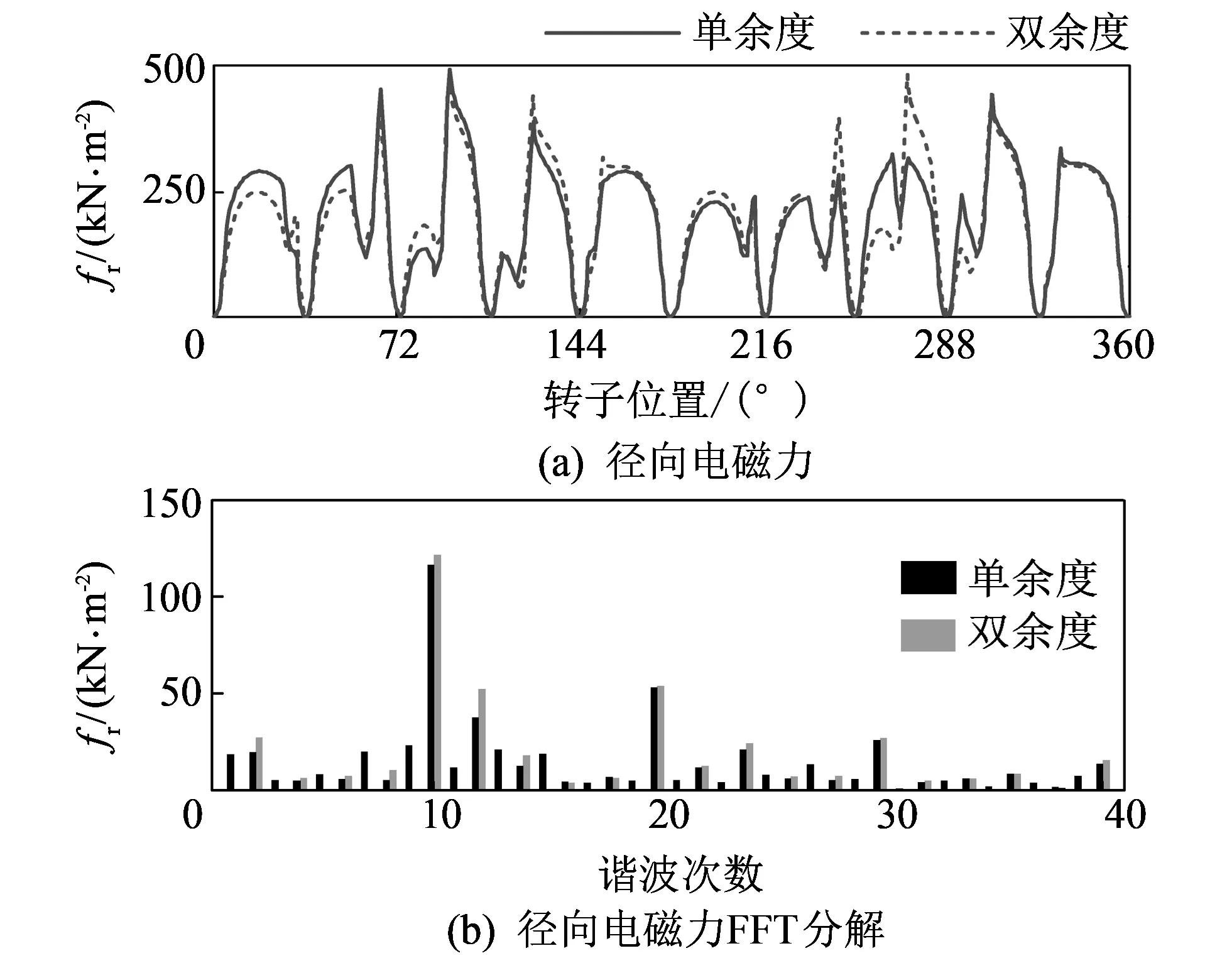
图 6 两种工况下的径向电磁力及其FFT分解Fig.6 Radial electromagnetic force of stator inner surface and its FFT decomposition in two conditions
从图 6 可知, 两种工作状态下, 径向电磁力的差别不仅是在幅值上的不同, 更重要的是所含电磁力波阶数的不同. 正常运行时, 只含有阶数为偶数的电磁力波, 而故障后单余度运行时, 含有所有阶数的电磁力波. 由上对电枢反应磁场的分析可知, 单余度运行后电枢反应磁场产生了除3的倍数外的所有极对数的径向磁密谐波. 这些增加了的偶数次谐波与本身存在的奇数次谐波就产生了阶数为奇数的电磁力波, 比如1次磁密谐波与2次磁密谐波相互作用就会产生阶数为1的电磁力波, 1次磁密谐波与4次磁密谐波相互作用就会产生阶数为3的电磁力波.
总结以上分析和仿真结果, 电机在双余度和单余度运行状态下的气隙磁场和电磁力的各次谐波如表 2 所示.

表 2 两种工况下双余度电机内部力波阶数
3 定子电磁振动分析
由经典力学理论可知, 任何线性机械系统结构的机械振动动力学通用方程为

(11)
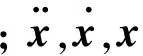
双余度电机定子内部的电磁力就是电磁振动的激励源. 将电磁仿真得到的两种工况下的电磁力分别耦合到二维结构有限元模型中, 对其进行瞬态结构动力学仿真分析.
在电磁力耦合环节中, 定子大齿离散为10个点. 将每个离散点的径向电磁力作用到电机动力学模型中进行计算. 振动仿真在电机额定转速下进行, 建立电机定子的结构有限元模型如图 7 所示.
在仿真计算中, 电机转速为3 600 r/min, 定子阻尼比为ζm, 且保持恒定.ζm由电机定子的固有模态频率fm采用以下经验公式求得,
ζm=(2.76×10-5fm+0.062)/(2π).(12)

图 7 定子铁心结构有限元模型Fig.7 Structure FEM of stator core
现只研究图 7 中定子外表面上一点H(0, 60)的振动位移. 待电机振动达到稳定状态后得到H点在正常运行和故障后单余度运行时的x和y方向的振动位移图像.H点x,y方向上随时间的振动位移及其FFT分解如图 8 所示.
从图 8 可以看出, 双余度电机无论在正常运行还是故障后单余度运行时,x和y方向的位移主波都是600 Hz的位移波. 单余度运行后,x方向的振动位移不仅在幅值上大幅度减小, 幅值减少幅度达到19.8%, 同时出现了一定程度的振动偏心和相移的情况, 这主要是由1阶径向电磁力波造成的. 而y方向上的振动位移幅值增大了10.3%. 由于H点位于绕组A1相的正上方, 单余度运行为了保证有足够的输出转矩, A1相的电枢电流更大, 产生更大的气隙磁密, 从而使结构仿真中的激励——径向电磁力更大, 使H点的y向振动更强.

图 8 H点x, y方向的振动位移及其FFT分解Fig.8 Vibration displacement in x and y direction and its FFT decomposition of H point
4 结 论
1)双余度电机定子表面径向磁密不仅是转子位置的函数, 也是时间的函数, 因此电机定子内表面的径向电磁力是随转子位置和时间变化的力波.
2)双余度电机定子内表面的电磁力由永磁磁场单独作用、 电枢反应磁场单独产生以及永磁磁场与电枢反应磁场共同作用产生三部分组成.
3)双余度电机在故障后单余度运行时, 电枢反应产生的气隙磁密不仅在幅值上发生了变化, 同时在谐波次数上也更加丰富.
4)电机单余度运行后, 气隙磁密谐波次数的丰富直接使电磁力波阶数增加, 从而造成电机在振动时存在一定程度上的偏心.
参考文献:
[1] Zhu Z Q, Xia Z P, Wu L J, et al. Analytical modeling and finite-element computation of radial vibration force in fractional-slot permanent-magnet brushless machines[J]. IEEE Transactions on Industry Application, 2010, 46(5): 1908-1918.
[2] Zhu Z Q, Howe D, Chan C C. Improved analytical model for predicting the magnetic field distribution in brushless permanent magnet machines[J]. IEEE Transactions on Magnetics, 2002, 38(1): 229-238.
[3] Zhu Z Q, Xia Z P, Wu L J, et al. Influence of slot and pole number combination on radial force and vibration modes in fractional slot PM brushless machines having single- and double- layer windings[C]. Energy Conversion Congress and Exposition, IEEE, 2009: 3443-3450.
[4] 杨浩东, 陈阳生, 邓志奇. 永磁同步电机常用齿槽配合的电磁振动[J]. 电工技术学报, 2011, 26(9): 24-30.
Yang Haodong, Chen Yangsheng, Deng Zhiqi. Electromagnetic vibration of PM synchronous motors with different combinations of slot and pole number[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 24-30. (in Chinese)
[5] 杨浩东, 陈阳生. 分数槽永磁同步电机电磁振动的分析与抑制[J]. 中国电机工程学报, 2011, 31(24): 83-89.
Yang Haodong, Chen Yangsheng. Electromagnetic vibration analysis and suppression of permanent magnet synchronous motor with fractional slot combination[J]. Proceedings of the CSEE, 2011, 31(24): 83-89. (in Chinese)
[6] Yang H D, Chen Y S. Influence of radial force harmonics with low mode number on electromagnetic vibration of PMSM[J]. IEEE Transactions on Energy Conversion, 2014, 29(1): 38-45.
[7] Hur J, Chun Y D, Lee J, et al. Dynamic analysis of radial force density in brushless DC motor using 3-D equivalent magnetic circuit network method[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3142-3145.
[8] 倪明明, 廖连莹, 左言言, 等. 车用永磁电机电磁振动与噪声分析[J]. 微特电机, 2015, 43(3): 9-13.
Ni Mingming, Liao Lianying, Zuo Yanyan, et al. Electromagnetic vibration and noise analysis of permanent magnet motor for vehicle[J]. Small and Special Electrical Machines, 2015, 43(3): 9-13. (in Chinese)
[9] 翁双安. 电机气隙时间谐波磁场引起的电磁振动分析[J]. 微特电机, 1997, 25(2): 22-23.
Weng Shuangan. Analysis of electromagnetic vibration caused by the time harmonic magnetic field of motor air gap[J]. Small and Special Electrical Machines, 1997, 25(2): 22-23. (in Chinese)
[10] Huang S, Aydin M, Lipo T A. Electromagnetic vibration and noise assessment for surface mounted PM machines[C]. Power Engineering Society Summer Meeting, IEEE, 2001: 1417-1426.
[11] Zhu Z Q, Ishak D, Howe D, et al. Unbalanced magnetic force in permanent magnet brushless machines with diametrically asymmetric phase windings[J]. IEEE Transactions on Industry Applications, 2007, 43(6): 1544-1553.
[12] Wang J, Xia Z P, Long S A, et al. Radial force density and vibration characteristics of modular permanent magnet brushless AC machine[J]. IEEE Proceedings on Electric Power Applications, 2006, 153(6): 793-801.
[13] Shin H J, Choi J Y, Park H I, et al. Vibration analysis and measurements through prediction of electromagnetic vibration sources of permanent magnet synchronous motor based on analytical magnetic field calculations[J]. IEEE Transactions on Magnetics, 2012, 48(11): 4216-4219.
[14] 周勰, 陈益广. 基于场路耦合的双余度永磁同步电动机特性仿真分析[J]. 微特电机, 2015(8): 40-44.
Zhou Xie, Chen Yiguang. Analysis of dual redundancy permanent magnet synchronous motor's performance simulation based on field-circuit coupling[J]. Small and Special Electrical Machines, 2015(8): 40-44. (in Chinese)

