N型反应装甲对射流干扰的数值模拟研究

李 优， 王凤英， 阮光光， 吴育智

(中北大学 环境与安全工程学院， 山西 太原 030051)

0 引 言

近几年的局部战争表明坦克和装甲车辆等现代装甲目标仍是地面战场上的主要突击兵器和装甲兵的基本装备， 它集火力、 防护性、 机动性、 通信能力于一身， 主要用于突破敌方防线， 消灭敌方步兵， 以及与敌人的坦克和其他装甲战斗车辆作战[1]. 爆炸反应装甲是由“三明治结构”的平板装药组合而成， 其中“三明治结构”的平板装药是指两块金属板中间夹层惰性炸药. 在聚能射流和穿甲弹的冲击下， 夹层炸药爆炸后驱动金属板， 使其获得动能从而干扰来袭射流或穿甲弹， 从而减低来袭弹药的毁伤能力. 由于爆炸式反应装甲具有体积小、 质量轻、 成本较低、 安全系数高等优点， 在现代装甲车辆的防护中得到广泛应用[2]. 伴随着反装甲弹药的不断推进， 大口径聚能装药、 串联战斗部、 隔板装药等技术在破甲弹上的应用大大提高了破甲弹的毁伤能力， 因此对爆炸式反应装甲也有了更高的标准. 传统结构的反应装甲结构一般为单层平板装药、 楔形平板装药或者多层平行板装药等， 已经不足以应对新型破甲弹战斗部对目标的毁伤能力. 如Mayseless等[3]对单层反应装甲干扰射流作用过程进行了深入的研究. 刘宏伟等[4]提出了垂直和斜侵彻单层爆炸反应装甲干扰射流模型， 并分析了双层平行反应装甲和V型反应装甲干扰射流的机理. 姬龙等[5]总结了双层楔形爆炸反应装甲飞板的运动规律. 但对于N型夹层炸药干扰射流侵彻的研究还较少.

本文提出了N形反应装甲结构并通过数值仿真模拟的方法对N形反应装甲干扰聚能射流的过程进行了研究， 分别讨论了聚能射流的入射角和N形反应装甲的平板装药夹角对其干扰射流能力的影响， 并得出了最佳平板装药夹角以提高N形反应装甲的防护能力， 为今后新型反应装甲的研究制备工作提供借鉴参考.

1 射流作用数值模拟

1.1 仿真模型的建立

仿真模型由主装药、 药型罩、 空气域、 后效靶板和呈N形安装的平板装药组成. 其中， 模型的基本结构参数如下： 主装药直径56 mm， 装药高度73 mm， 药型罩口部直径54 mm， 药型罩壁厚1 mm， 药型罩锥角60°， 炸高80 mm. N形反应装甲由3块平板装药按一定的夹角、 间距方向组合而成； 3块平板装药的夹层炸药选择为3 mm-2 mm-3 mm 的组合方式， 聚能射流与平板装药的法线角(NATO角)为45°， 平板装药间距均为5 mm. 分别模拟了夹角为5°， 7°， 9°， 13°， 15°和平行6种情况， 并分析了通过反应装甲后的残余射流对主靶板的侵彻过程. 不同夹角的N形反应装甲仿真模型如图 1 所示.

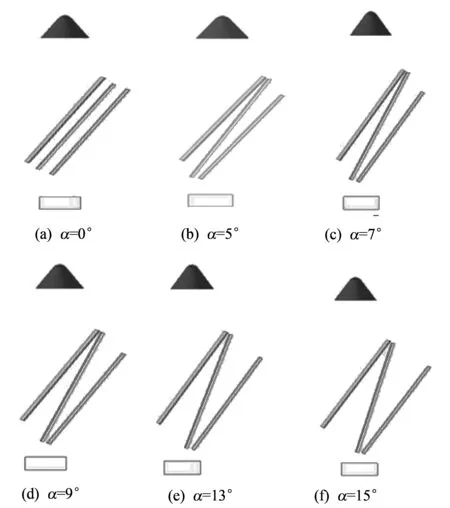
图 1 不同夹角的N形反应装甲仿真模型Fig.1 N-shaped reactive armor simulation model with different angles

1.2 材料参数

由于射流与靶板间是高速碰撞的作用过程， 因此在侵彻中出现了大应变、 大变形、 高应变率的现象. 为避免网格变形过大造成负体积和计算中止现象， 聚能装药、 药型罩、 空气采用ALE算法， 后效靶板和平板装药采用Lagrange算法， 对于夹层炸药采用附带失效方程描述， 当炸药爆轰体积膨胀到一定程度时自动删除炸药网格.

计算时， 药型罩采用steinberg模型和Gruneisen状态方程共同描述； 主靶、 面板与背板均采用Johnson-Cook模型和Gruneisen状态方程共同描述； 主装药选用JWL状态方程， 运用流体弹塑性模型及点火与增长方程共同描述夹层炸药.

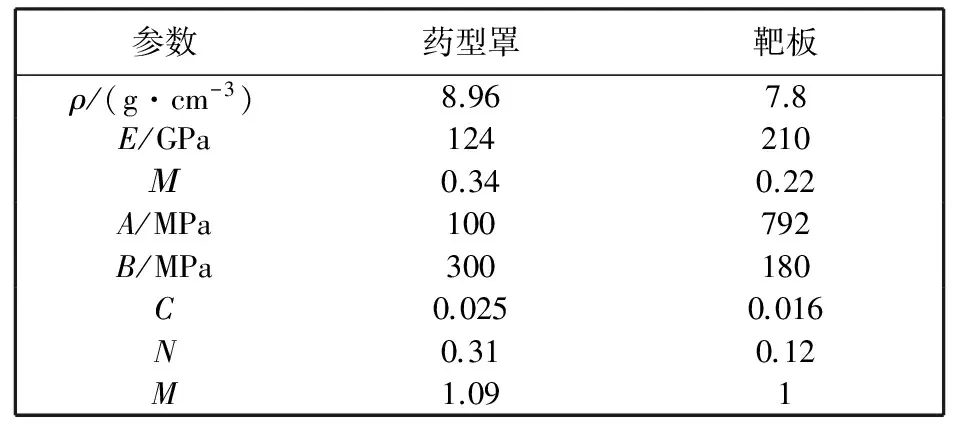
表 1 材料基本参数

表 2 主装药材料状态方程参数

表 3 夹层装药材料状态方程参数

2 模拟结果分析

2.1 N型夹角对射流的干扰分析

李如江等[6]对聚能射流侵彻爆炸反应装甲的入射角进行了深入的研究. 单层平板装药对聚能射流的干扰效果最佳时， NATO角为60°. 本节主要讨论N形反应装甲的夹角对其干扰聚能射流能力的影响规律， 因此固定聚能射流侵彻N形反应装甲的NATO角为60°， 改变N形反应装甲的平板装药间夹角. 图 2 是入射角为60°、 N形反应装甲的平板装药夹角分别为0°， 5°， 7°， 9°， 13°， 15°时， 射流侵彻N型夹层炸药的典型时刻状态图. 不同角度下射流的头部速度如表 4 所示.

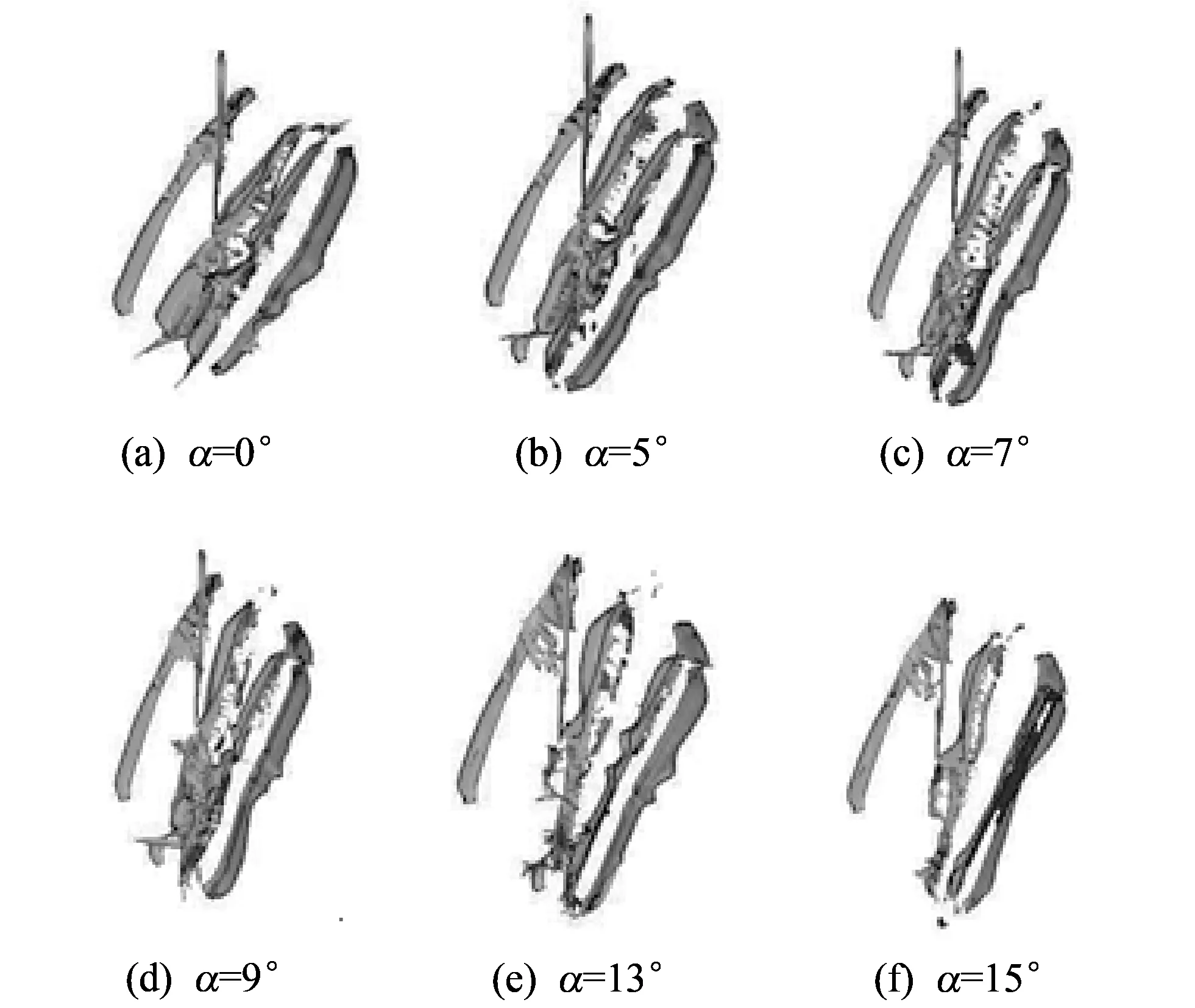
图 2 射流与N型反应装甲作用图Fig.2 Action diagrams of jet-flow and N-shaped reactive armor

角度/(°)射流最终头部速度/(m·s-1)01730516507180091900132010152100

射流通过N型夹层炸药， 首先引爆上层夹层装药， 炸药起爆后， 夹层炸药驱动两侧金属板， 使其沿法线方向飞散[7-9]. 在飞行中金属板对斜侵彻的射流产生干扰作用， 射流偏离了轴线方向， 同时发生弯曲， 最终形成了更多的断裂射流， 由于两板间角度较小且距离较近， 受到射流和上层爆轰形成的压力及上层背板的共同作用， 上层背板很快就与中层面板发生塑性碰撞， 使飞板消耗射流的时间减少[10]. 上层飞板的碰撞引爆第二层夹层炸药， 从而驱动中层面板和背板相向运动， 在射流未完全加速完成时， 中组背板和下组面板发生碰撞并焊接在一起， 正是这种爆炸焊接作用， 使N型反应装甲相对于V型反应装甲对射流的防护效果更好.

N型反应装甲干扰聚能射流与V型反应装甲和多层变角度反应装甲的作用原理类似， 只是聚能射流的变形程度和速度降低幅度以及聚能射流对后效板的作用效果不同.

由表 5 和图 3 可知， 对于射流入射角度60°， 侵彻不同N型角平板装药结构时， 射流的侵彻能力随夹角的增大呈上升趋势. 当N型角为 15° 时， 由于入射角固定夹角增大， 射流只穿过上、 中两组飞板， 从图中可以明显看出， 从飞板出来的射流只有4个弯曲段， 所以消耗射流的能力减弱， 侵彻深度增加. 随着夹角的增大， 反应装甲对射流的防护效果越差， 在平板装药夹角为5°时， 防护效果最为明显.

图 3 不同角度下侵彻后效靶板效果图Fig.3 Effects of penetrating post-effect targets at different angles

角度/(°)射流最终头部速度/(km·s-1)后效靶板的侵彻深度/mm05000．7558000．26713501．19917001．661317502．261518001．81

2.2 N型夹层炸药爆炸后飞板的飞散特性分析

通过射流引爆N型夹层炸药， 分别测量了各组面板、 背板的飞散速度. 图 4 分别是平板装药药夹角为9°， 13°， 15° 时6块飞板的飞散速度曲线图. 平板装药被射流引爆后， 爆轰产物向外迅速膨胀， 在爆轰波的驱动作用下， 反应装甲面、 背板沿各自法线方向向外飞散.

图 4 各角度下飞板飞散速度曲线图Fig.4 Radial velocity curve of flying board at different angle

夹层炸药爆炸后， 爆轰产物作用于面板和背板， 使面、 背板从中心开始发生局部凸起[11-13]. 首先被射流引爆的N型平板装药中的上层反应装甲的飞板向外运动， 穿过上层反应装甲的射流继续侵彻并引爆中层反应装甲， 驱使中层反应装甲飞板发生运动， 穿过中层反应装甲后的剩余射流将继续侵彻并引爆下层反应装甲， 驱使下层反应装甲飞板运动. 三层反应装甲间有一定的间隔距离， 使各夹层炸药引爆时间不同， 飞板的初始运动也存在一定的时间差[14-16]. 对于N型反应装甲， 其中上层反应装甲的背板与中层反应装甲的面板、 中层反应装甲的背板和下层反应装甲的面板均有相互碰撞的可能性. 在两板接触之前是相互独立的两组件的运动， 而碰撞之后， 根据完全塑性碰撞理论， 焊接在一起的两板就像以较低速度运动的单板一样. 由图4知， 对射流防护能力最明显的是中间靶板.

3 结 论

由于N型反应装甲有多层平板装药， 每层飞板均与射流有接触， 干扰射流的过程变得更加复杂， 运动的飞板与射流产生相互作用的同时， 各飞板间也会接触并发生碰撞作用. 通过对侵彻带有N型夹层炸药的靶板的数值模拟， 可得出以下结论：

1) 在射流入射角为60°， 侵彻不同N型夹角平板装药结构时， 射流的侵彻能力随着夹角的增大呈上升趋势. 当夹角大于9°后， 夹角对残余射流的侵彻深度变化并不敏感.

2) 随着N型夹角的增大， 射流对主靶的侵彻深度增加， 反应装甲对射流的干扰减小. 当N型夹角为5° 时， 防护效果最好.

3) 对于N型夹层炸药的结构， 相比于单层爆炸反应装甲， 其飞板数量增多， 对射流产生更强的干扰作用， 从而造成射流断裂并发生严重偏转， 大幅度减小射流的侵彻深度.

参考文献：

[1] 李向东， 沈培辉. 弹药概论[M]. 北京： 国防工业出版社， 2010.

[2] 高学浩， 王凤英， 刘天生， 等. V型夹层炸药干扰杆式侵彻体的影响因素研究[J]. 弹箭与制导学报， 2014， 34(1)： 87-89.

Gao Xuehao， Wang Fengying, Liu Tiansheng, et al. Study on influencing factors of V-type sandwich explosive interfere in rod-type penetrating body[J]. Journal of Projectiles， Rockets， Missiles and Guidance， 2014， 34(1)： 87-89. (in Chinese)

[3] Mayseless M， Erlich Y， Falcovitz Y, et al. Interaction of shaped-charge jet with reactive armour[C]. Proceedings of 8th International Symposium on Ballistic， Orlando Florida， 1984, 7: 15-20.

[4] 刘宏伟， 夏松林， 赵靖. V型反应装甲与射流作用过程分析[J]. 兵器材料科学与工程， 2011， 34(4)： 20-22.

Liu Hongwei， Xia Songlin, Zhao Jing. The analysis of V-type reactive armor with jet process[J]. Ordnance Material Science and Engineering， 2011， 34(4)： 20-22. (in Chinese)

[5] 姬龙， 黄正祥， 顾晓辉. 双层楔形爆炸反应装甲飞板的运动规律[J]. 爆炸与冲击， 2013， 33(4)： 387-393.

Ji Long， Huang Zhengxiang, Gu Xiaohui. The movement law of double-deck wedge-shaped explosion reaction armored[J]. Explosion and Shock Waves， 2013， 33(4)： 387-393. (in Chinese)

[6] 李如江， 沈兆武. NATO角和飞板速度对平板装药干扰射流频率的影响[J]. 含能材料， 2008， 16(3)： 295-297.

Li Rujiang， Shen Zhaowu. Effect of NATO angle and plate velocity on disturbance frequency of reactive armor aganist shaped charge jet[J]. Chinese Journal of Energetic Materials， 2008， 16(3)： 295-297. (in Chinese)

[7] Nicholson L S， Rogers M C， Cox R J， et al. The use of analystical shaped charge jet and target response mode to predict the efficiency of jet disruption by single and multiple explosive armour targets[C]. Proceedings of 8th International Symposium on Ballistic, 1984.

[8] 吴鹏， 李如江， 阮光光， 等. 弹着点位置对V形反应装甲干扰射流的影响[J]. 高压物理学报， 2018, 32(1)： 1-7.

Wu Peng, Li Rujiang, Ruan Guangguang, et al. Impact of the position of the impact point on the V-shaped reaction armor jamming jet[J]. Chinese Journal of High Pressure Physics, 2018, 32(1)： 1-7. (in Chinese)

[9] 张乐. 某结构反应装甲对射流干扰的机理研究[D]. 南京： 南京理工大学， 2016.

[10] 武海军， 陈利， 王江波， 等. 反应装甲对射流干扰的数值模拟研究[J]. 北京理工大学学报， 2006， 26(7)： 565-568.

Wu Haijun， Chen Li， Wang Jiangbo, et al. Numerical simulation study on jet interference of reaction armor[J]. Journal of Beijing Institute of Technology， 2006, 26(7): 565-568. (in Chinese)

[11] 甄金鹏. 平板装药飞板运动规律的数值模拟及研究[D]. 太原： 中北大学， 2010.

[12] 张乐， 姚文进， 王晓鸣， 等. 隔板对双层平行反应装甲金属板运动影响[J]. 机械制造与自动化， 2017， 43(6)： 106-109.

Zhang Le, Yao Wenjin， Wang Xiaoming, et al. Influence of separator on the movement of double parallel armored metal plates[J]. Machinery Manufacturing and Automation, 2017, 43(6): 106-199. (in Chinese)

[13] 侯辉， 姚文进， 李文彬， 等. 新型双层反应装甲金属板运动分析与研究[J]. 弹道学报， 2017， 29(2)： 34-38.

Hou Hui, Yao Wenjin, Li Wenbin, et al. The motion of analysis and research on a new type of double-layer reactive armored metal plate[J]. Journal of Ballistics， 2017, 29(2): 34-38. (in Chinese)

[14] 刘宏伟. 爆炸反应装甲飞板变形及干扰射流模型[D]. 南京： 南京理工大学， 2007.

[15] 李辉， 张峰庆. 适用装甲车辆的爆炸反应装甲研究[J]. 山西化工， 2016, 36(1): 44-46.

Li Hui, Zhang Fengqing. Research on armored explosive reactive armor for armored vehicles[J]. Shanxi Chemical Industry， 2016, 36(1): 44-46. (in Chinese)

[16] 余晖， 刘天生， 王凤英， 等. 基于正交设计法的爆炸反应装甲优化设计[J]. 兵器材料科学与工程， 2015， 11(6)： 70-74.

Yu Hui, Liu Tiansheng, Wang Fengying, et al. Orthogonal design based explosion response armor optimization design[J]. Ordnance Material Science and Engineering， 2015， 11(6): 70-74. (in Chinese)