基于道路交通安全综合风险水平的城市模糊聚类评价

赵学刚

(山西警察学院 交通管理系， 山西 太原 030021)

0 引 言

城市是一个受多因素影响而不断变化的动态系统[1]. 城市系统内部模块要素众多， 相互之间影响、 作用复杂. 因此， 一个城市又是一个复杂巨系统. 不同城市系统中的众多模块要素的相互影响与作用形成了每个城市系统独有的特点； 同时， 不同城市系统的规模[2]、 经济、 土地利用[3]等发展不平衡， 导致城市系统对其子系统的影响作用呈现出较大的差异性. 因此， 针对地理环境、 环保等领域， 已经开展了城市系统对其子系统的具体影响作用研究[4]. 城市道路交通安全综合风险控制系统是城市系统的一个重要子系统， 如何评价城市系统对该系统的影响作用， 对于客观、 科学地开展城市道路交通安全风险的横向评价具有重要的意义.

目前， 在国内外大多数关于区域道路交通安全状况的横向宏观评价研究中， 评价的重点基本都是对区域道路交通安全的管理效果[5-6]， 而且在这些横向评价研究中， 并没有针对性地研究区域的不同规模、 不同状况对安全状况的影响作用. 但是， 实施不同城市交通安全管理评价， 如城市“畅通工程”评价及不同城市交通应急机制等研究[7-8]， 以及作者前期在评价不同城市的道路交通安全风险状况[9]等相关研究中， 都已经涉及到城市系统特点对其交通安全子系统的影响作用. 在这些文献中， 横向评价城市交通安全时， 涉及到城市系统对其交通系统或交通安全综合风险控制系统的影响作用的， 采用的方法均是以城市的规模为依据进行分类评价. 具体方法都是直接套用国家对城市规模的分类标准， 不同类型城市对应不同影响作用等级. 然而， 这种对城市的分类， 仅仅依据的是城市人口(或国民生产总值)单一指标的规模分类[2]. 将这种简单的城市规模分类结果用于其对道路交通安全风险控制系统的影响作用评价， 很容易出现偏误[10]. 综合国内外相关研究来看， 城市系统对其道路交通安全综合风险控制子系统的影响作用虽然具有重要的理论与实践意义， 但目前的相关研究还相当有限.

本文应用系统动力学相关理论， 分析城市系统对其道路交通安全综合风险控制子系统的影响作用； 通过研究风险控制系统受作用于城市系统的特定表征指标， 以此构建具有正相关性的城市聚类评价指标体系； 依据评价指标体系和城市系统间影响作用横向评价需求， 进一步研究相应的聚类评价方法. 该聚类评价方法突破了之前的单一评价指标模式， 是建立在城乡人口比、 民用汽车拥有量、 公共汽电车客运量、 公路货运量、 公路里程、 城市道路面积、 城市建成区面积、 国内生产总值等8个指标评价体系基础上的综合评价法. 该综合评价方法实现了城市系统对其道路交通安全综合风险控制子系统影响作用的等级量化评价， 其结果可以为城市风险控制决策提供科学依据.

1 城市系统对其风险控制系统影响作用分析

1.1 城市系统交通安全综合风险控制模型

在社会发展进程中， 城市(或城镇， 下同)逐渐成为社会组织的主要区域性单元. 随着社会城镇化程度的提高， 城市系统已经成为社会系统的主要构成和存在形式， 因此， 城市将是社会管理的主要功能单元. 城市道路交通安全综合风险控制系统(简称风险控制系统)作为城市系统的子系统， 是建立在道路交通系统、 驾驶人-车辆系统、 交通安全管理系统及交通安全风险系统基础上的复合系统； 其系统构成要素包括人-车、 道路、 环境、 交通流、 交通安全管理、 交通组织控制、 交通安全决策及人-物等[11]. 从宏观来看， 城市系统承担社会功能必然生成道路交通安全综合风险. 风险控制系统作为城市系统的子系统， 其功能就是调节、 控制城市系统中的道路交通安全综合风险. 从风险控制系统结构来看， 通过对系统输出的道路交通安全风险偏差确定并转化为预警信号， 可以建立系统的反馈回路[11]. 根据系统动力学原理[12]， 构建该系统的反馈闭合环路， 可以实现对城市系统道路交通安全综合风险的动态控制. 具体的控制作用过程是， 风险控制系统对城市系统输入的高势能道路交通安全风险(即城市道路交通安全综合风险， 简称为综合风险或输入风险)进行控制， 输出低势能道路交通安全风险(简称为控制风险或输出风险). 城市道路交通安全综合风险控制模型见图 1.

1.2 系统间作用分析

由图 1 可知， 风险控制系统的功能是对城市系统道路交通安全综合风险管理， 城市系统的输入风险是管理与控制对象.

图 1 城市道路交通安全综合风险控制模型Fig.1 A comprehensive risk control model for urban road traffic safety

该系统控制目标是使城市系统的输出风险水平趋于城市系统需要的某种状态. 系统输出风险水平与系统控制效率和系统输入风险水平相关. 一般情况下， 控制系统的控制效率相对稳定， 系统的输出风险水平和输入风险水平成正相关关系. 从风险控制系统的具体构成系统及其中的各要素来看， 它们都受到城市系统中经济状况、 产业分布、 人口状况、 地理环境、 道路状况、 科技水平及政府相关政策等众多因素影响. 故而， 城市系统的规模、 城市化水平、 城市类型、 特性等对该控制系统的运行均具有较大影响作用. 从城市系统角度看， 不同城市系统具有不同的经济、 人口等社会经济情况[13]， 不同社会经济情况生成的综合风险必然不同， 其生成的综合风险对于风险控制系统即为输入风险. 因此， 不同城市系统具有不同的输入风险； 城市道路交通安全综合风险即为城市系统的生成风险. 由图 1 可知， 城市系统对其风险控制系统的影响作用， 就直接表现为城市系统对其子系统的输入风险， 即城市道路交通安全综合风险， 也可以称为城市系统的生成风险. 综上所述， 城市系统的生成风险， 即城市道路交通安全综合风险， 就是城市系统影响作用于风险控制系统的直接反映； 城市道路交通安全综合风险越大， 城市系统对风险控制系统的影响作用越大. 可以将城市道路交通安全综合风险水平(简称为综合风险水平)作为这一作用的一个表征量， 进一步定量研究城市系统对其风险控制系统的影响作用.

1.3 城市系统综合风险水平分析

1.3.1 风险度量

根据道路交通安全风险理论研究成果[9，11，14]， 在城市系统的风险控制子系统中， 控制风险是在一定时期该系统内部所有构成要素风险的耦合结果. 城市系统控制风险基本度量形式为

R=(g1,g2,…,gn)·(r1,r2,…,rn)T,(1)

式中：R为控制风险；ri为要素风险源的风险，ri=ri(hi,pi,di)(i=1,2,…,n)，pi为要素风险源风险发生的概率，di为要素风险源可能造成的风险损失，hi为要素风险源的子风险源风险；gi表示要素风险源风险在合成综合风险时的函数关系， 与时间、 要素风险源数量等有关. 由此可见， 控制风险水平取决于其风险概率与风险损失， 而且与它们正相关.

1.3.2 综合风险水平特性及表征指标分析

城市系统综合风险水平基本度量形式雷同于城市系统控制风险， 正相关于其风险概率与风险损失. 考虑城市系统输入风险和输出风险的正相关关系， 以及控制系统的控制效率和输入风险概率在一定时期内具有相对稳定性的特点， 城市系统综合风险水平可以借助控制风险(输出风险)的风险损失进行量化分析. 风险损失虽然在管理控制中是未来事件， 但是与已经发生的道路交通事故的损害后果具有相对稳定的正相关关系. 因此， 最终选用道路交通事故的绝对损害系数作为综合风险水平的量化表征指标. 道路交通事故绝对损害系数(简称绝对损害系数)具体是指， 一定范围及时期内道路交通事故(风险事件)造成的平均损害程度， 可以用一定时期内的绝对经济损失表示. 该系数越大， 表明这一时期及范围系统综合风险中风险损失越大， 相应的综合风险也越大， 综合风险水平越高. 其计算式(2)为

AH+L/Q′,(2)

式中：S为道路交通事故绝对损害系数；D为统计范围及周期内交通事故造成的死亡人数；AD为交通事故造成人员死亡转为经济损失系数， 可以结合国家相关规定确定为20[15]；AH为交通事故造成人员受伤转为经济损失系数， 可以结合国家相关规定确定为10[15]；f,d为统计范围及周期内城镇居民人均可支配收入、 农村居民人均纯收入(单位为万元)；Q为统计范围及周期内事故起数.

利用式(2)计算我国2004年～2013年的绝对损害系数. 所需原始数据来源为《中国统计年鉴》(2004～2013)， 计算结果见表 1.

表 1 我国2004年～2013年的道路交通事故情况

由表 1 数据分析可知， 2004年～2013年期间， 我国道路交通事故统计死人数、 起数指标均呈现出逐年递减趋势， 但交通事故的绝对损害系数逐年递增. 由绝对损害系数与道路交通安全综合风险水平的正相关关系， 表明近年来全国道路交通安全综合风险水平整体呈现上升趋势. 具体分析， 这一时期我国道路交通系统整体呈现规模快速扩大趋势， 导致其综合安全风险加大， 符合风险生成的基本规律. 由以上分析可知， 随着近年来我国城镇化程度的逐年提高， 我国城市的综合风险水平总体呈现上升趋势. 因此， 可以选用道路交通事故绝对损害系数作为城市的综合风险水平的相关性表征指标.

2 评价指标体系构建

2.1 评价方法及指标体系设计思路

由前述可知， 交通事故的绝对损害系数与综合风险水平具有正相关关系， 将其作为表征风险控制系统受作用于城市系统的特定指标， 可以此构建具有正相关性的综合风险水平评价指标体系. 借助城市范围具体时期相应指标统计数据， 根据指标与综合风险水平的正相关性这一特点， 采用聚类分析的方法对这一时期不同城市的综合风险水平进行横向评价. 指标体系构建的基本思路是， 以道路交通事故的绝对损害系数为参照， 以风险控制系统的构成要素风险源为指针， 具体分析城市系统中具有直接作用的要素选取指标， 即一般选取具有相关关系的绝对指标. 考虑指标选取的可获得性和城市统计数据的可行性， 以及统计取样尽可能长时期大范围的原则， 在我国现有国家统计指标体系中进行选择构建.

2.2 指标体系构建

在确定指标时， 为考虑控制系统的控制效率和输入风险概率在一定时期内具有相对稳定性的特点， 选取全国范围内2004年～2013年的交通事故统计数据， 计算道路交通事故的绝对损害系数， 结果见表 1. 依照风险控制系统的8个构成要素， 在我国国家统计指标中人工初选. 对应风险控制系统的8个构成要素， 可以初选出12个统计指标. 将12个统计指标数据对表 1 中的绝对损害系数进行相关性识别. 选择在显著性水平为0.01时的Pearson系数大于0.8的指标， 在此基础上再对其进行有效性t检验(大于t0.005(8)=3.355 4)， 最终遴选出其中相关性较强的指标. 选取《中国统计年鉴》(2004～2013)中相关统计指标的原始数据， 借助SPSS软件对数据进行处理， 结果见表 2.

表 2 最终遴选指标的Pearson系数及t检验

由表 2 可知， 对应控制系统的8要素(因部分要素在现有统计体系中无明显对应统计指标， 可将其合并为其他类构成要素， 待完善统计体系后可再补充完整)， 共选取了符合要求的9个相关指标. 考虑到乡村人口指标的负相关性， 将其与城镇人口指标合并为一个指标， 即城乡人口比(城镇人口数与乡村人口数的比值). 最终由8个指标构成了控制系统的要素相关指标体系， 作为正相关的综合风险水平评价指标体系. 为了验证这8个指标体系与城市道路交通安全综合风险的复合相关性， 再次识别它们与绝对损害系数数据的复相关系数. 借助SPSS软件计算可得复相关系数为1， 显著性水平为0.05时有效性F检验值为4 851.248， 远大于标准值F0.05(1,8)=238.9， 复相关检验有效. 由此可知， 该指标体系中所有指标与综合风险水平的具有高度正相关性.

2.3 指标权重计算

依据所构建指标体系与道路交通事故绝对损害系数的高度相关情况， 采用模糊相关系数法[16]计算各指标的权重值.

2.3.1 标定模糊相似矩阵A

在2004年～2013年统计数据中将指标体系中8个指标用相关系数法进行标定， 得到模糊相似矩阵A， 记为A=(aij)8×8， 这里aij(i,j=1,2,…,8)为

(3)

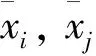
2.3.2 计算指标间多元相关系数ρi

第i个指标与其它7个指标间多元相关系数为ρi，

(4)

2.3.3 计算指标的权重ωi

第i个指标的权重为ωi， 计算公式为

(5)

应用该方法， 借助Matlab软件编程可以对原始数据进行处理计算出指标权重. 最终构建城市聚类评价指标体系及指标权重， 见表 3.

表 3 城市分类指标体系及指标权重

3 城市聚类评价方法

3.1 系统要素指标测度计算

按照表 3 构建的城市聚类评价的指标体系收集所要研究城市的具体统计期原始统计数据， 建立系统要素相关指标数据矩阵X=(xij)m×8，m为研究城市系统个数. 利用指标权重系数， 按照表3中控制系统要素类型为划分依据， 采用加权平均法， 获得m个城市系统的要素指标测度矩阵U=(uij)m×5， 计算公式为

(6)

式中：ωj*(j*=1,2,…,8)为式(5)中的ωi(i=1,2,…,8). 系统要素指标测度矩阵U=(uij)m×5的每个列向量对应风险控制系统要素指标， 它仍然保持了与城市系统的综合风险水平的正相关特性， 也可以反映出所有城市系统在单要素方面的影响作用.

3.2 模糊性标定

为了消除指标不同量级的影响， 且更好地利用各要素指标测度的原始数据统计信息， 对其采用标准差法与极值法进行二重标定， 获得矩阵B=(bij)m×5， 计算公式为

(7)

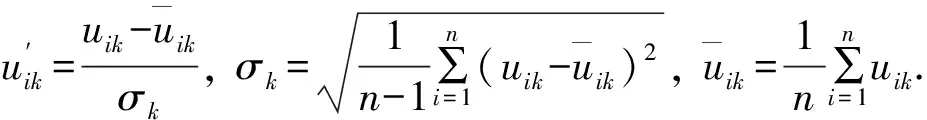
3.3 模糊C均值聚类分析

根据城市道路交通安全综合风险控制研究需要, 一方面考虑应该人为控制对所有研究城市系统的评价等级数， 另一方还需获得某一类型(等级)所表示的综合风险水平程度及各城市系统属于等级时的程度等信息， 比较现有各种硬聚类方法， 模糊聚类方法能够满足这些要求. 此外， 针对系统要素指标测度的标准化模糊矩阵B=(bij)m×5进行聚类分析， 该矩阵保留了系统要素指标测度的正相关特性； 考虑聚类方法应当能够根据聚类后所得类别之间对指标正相关特性差异的量化表达来确定每个类型的等级， 依此可以对城市系统的综合风险水平进行等级量化. 为此， 最终选择模糊C均值聚类法(FCM)[17]. 具体应用该方法时， 一般可以根据研究城市的实际情况人为确定城市的聚类数. 借助Matlab软件的FCM程序， 可以直接对系统要素指标测度的标准化模糊矩阵进行聚类分析， 最终得到研究城市的所属类别等级及属于该类别的隶属度(即程度).

3.4 聚类有效性检验及等级确定

对于模糊C均值聚类法的有效性检验可以应用Friedman检验[18]. 该方法利用聚类数和各城市全部指标分别属于每类型的隶属度作为检验依据. 具体方法是对模糊C均值聚类法所得模糊分区矩阵U进行Friedman检验， 99%置信区间统计量大于对应临界值即为有效. 在聚类有效前提下， 应用模糊C均值聚类结果确定各城市所属类型及等级. 具体方法是： 在Matlab运行程序输出的结果中， 聚类中心矩阵center各行的数值表示城市每个聚类类型各要素指标测度的中心坐标值； 行数为聚类数， 各行排列序号为系统默认聚类号码， 在Y中的用数值表示.Y中最后一行数值对应每个城市的所属类型号码，I中的数值对应为城市聚类类型号码的隶属度. 根据控制系统要素指标与系统综合风险水平的正相关特性， 每类型中指标聚类中心坐标center的这一特性可以用来确定该类型对应的等级. 即求聚类中心矩阵center中各行的中心坐标值的加权平均值， 所得数值(简称为等级值)的大小排序对应确定为程度等级， 即数值越大表明程度越高. 每个类型的程度等级可表示该类型城市系统综合风险水平， 最终以等级量化形式评价所有研究城市系统对其控制子系统的影响作用.

4 山西省地级城市聚类评价

4.1 系统要素指标测度计算

应用上述城市聚类评价所构建的指标体系及方法， 以山西省11个地级城市2012年度的9个相应指标统计数据为例， 进行实例应用. 根据《山西省统计年鉴》(2013)统计数据， 利用表3构建山西省地级城市要素相关指标数据矩阵X=(xij)11×8(因篇幅有限， 未列出)， 应用式(6)进行要素指标测度计算, 获得U=(uij)11×5(因篇幅有限， 未列出).

4.2 模糊性标定

利用式(7)， 对U=(uij)11×5进行模糊标准化标定， 借助Matlab软件计算， 获得要素指标测度标准化模糊矩阵B=(bij)11×5，

4.3 模糊C均值聚类分析

将山西省11个地级城市聚类数c定为4， 将B=(bij)11×5作为聚类数据， 借助Matlab软件运行FCM程序， 得到系统默认山西省地级城市聚类类型号码及其隶属度. 应用SPSS软件进行Friedman检验， 99%置信区间的统计量为14.018， 大于临界值11.345(查表所得)， 聚类有效. 根据聚类中心矩阵center的中心坐标的加权平均值， 确定程度等级由高到低排列为第一到第四类， 结果见表 4.

表 4 山西省地级城市聚类评价结果

4.4 山西省地级城市聚类评价结果分析

这11个城市都是山西省的地级城市， 按照现有城市规模划分标准(以城区人口指标划分)， 分为3类： 除太原市属于Ⅰ型大城市， 阳泉与朔州属于中型城市外， 其余都是Ⅱ型大城市. 但是由表 4 可知， 应用本文聚类评价方法所得基于综合风险水平的聚类结果来看， 可以分为4类， 与原有分类结果并不相同. 太原市属于第一类城市， 综合风险水平高， 且其隶属度为1， 说明该城市属于第一类的程度几乎是绝对的. 具体分析， 该市作为省会城市， 城市城乡人口比、 民用汽车拥有量、 公共汽电车客运量、 城市建成区面积、 国内生产总值等指标值均为最高值且远大于其他城市， 见表 5. 可见， 该城市规模远大于其他地级城市， 城市系统相对复杂， 系统生成综合风险最大， 该城市的综合风险水平最高， 其对风险控制子系统影响作用的程度最大. 第二类城市包括大同市、 晋城市和晋中市， 综合风险水平较高， 即系统生成风险水平较高, 其对风险控制子系统影响作用的程度较大. 它们的隶属度均大于0.8， 属于第二类的程度是肯定的. 具体分析， 这3个城市比较突出的情况是控制系统中道路要素值， 特别是指标权重最高的城市道路面积这一指标处于高水平(见表5)， 对于综合风险水平的影响程度较大. 第三类城市包括长治市、 运城市和临汾市， 这类型城市风险水平一般， 即系统生成风险水平一般； 其对风险控制子系统影响作用的程度一般； 隶属度均大于0.8， 属于第三类的程度是肯定的. 这3个城市多数指标处于中下水平(见表5)， 综合评价城市系统生成风险水平属于一般水平. 第四类城市包括阳泉市、 朔州市、 忻州市和吕梁市， 这类型城市综合风险水平低， 即系统生成风险水平低， 其对风险控制子系统影响作用的程度低； 其中阳泉市和吕梁市的隶属度均在0.5～0.8范围， 属于第四类的程度是基本肯定的， 朔州市、 忻州市属于第四类的程度是肯定的. 其中， 忻州市、 吕梁市的城乡人口比、 城市建成区面积两项指标处于最低水平， 民用汽车拥有量指标仅略高于阳泉、 朔州(见表5)， 可见将其与阳泉、 朔州归为一类是合理的. 以上这一评价结果是针对2012年， 根据每年相应的统计数据， 应用该方法还可以实现对山西省地级城市综合风险水平的动态评价.

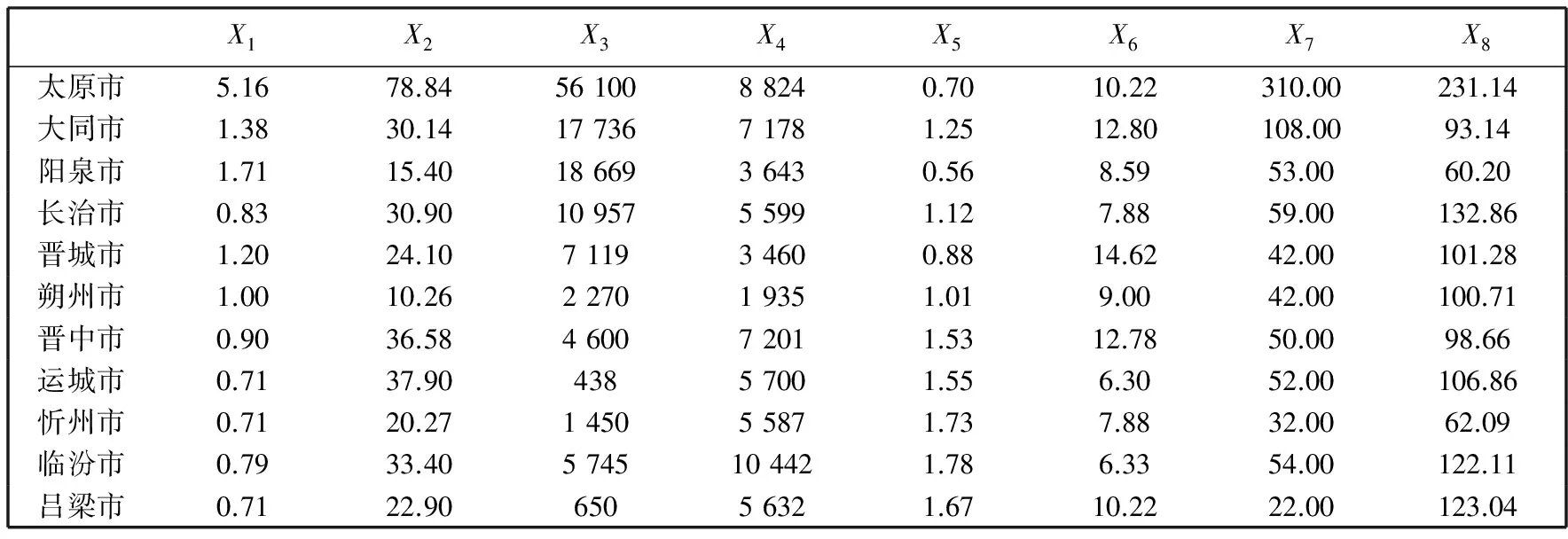
表 5 山西省11个地级城市2012年度的相关指标数据

5 结 论

1) 城市道路交通安全综合风险水平可以作为城市道路交通安全综合风险控制系统受制于城市系统的一个表征量； 道路交通事故绝对损害系数可以作为其相关性的表征指标.

2) 以道路交通事故的绝对损害系数为参照， 以城市道路交通安全综合风险控制系统的构成要素风险源为指针， 可以构建包括城乡人口比、 民用汽车拥有量、 公共汽电车客运量、 公路货运量、 公路里程、 城市道路面积、 城市建成区面积、 国内生产总值等8个具有正相关性的城市聚类评价指标体系.

3) 利用构建的城市聚类评价指标体系， 应用模糊C均值聚类法可以对不同规模城市系统进行聚类评价， 以此实现城市系统对其道路交通安全综合风险控制子系统影响作用的横向等级量化评价.

4) 应用本文的城市聚类评价方法， 可以实现基于道路交通安全综合风险水平的特定期间所研究区域范围不同城市系统的模糊聚类. 利用统计期变换可以实现对研究城市的动态评价. 这更有利于城市道路交通安全综合风险动态控制研究与管理实践.

5) 根据国家相关统计指标的补充健全， 应用本文指标体系构建方法还可以进一步完善所构建的聚类评价指标体系.

参考文献：

[1] 姜洋. 系统动力学视角下中国城市交通拥堵对策思考[J]. 城市规划, 2011, 35(11)： 73-80.

Jiang Yang. Reflections on anti-congestion policies in Chinese cities from system dynamics perspective[J]. City Planning Review, 2011, 35(11)： 73-80. (in Chinese)

[2] 孙晓, 刘旭升, 李锋, 等. 中国不同规模城市可持续发展综合评价[J]. 生态学报, 2016, 36(17)： 1-11.

Sun Xiao, Liu Xusheng, Li Feng, et al. Comprehensive evaluation of sustainable development for different scale cities in China[J]. Acta Ecologica Sinica, 2016, 36(17)： 1-11. (in Chinese)

[3] 谢奔一， 蒋惠园. 基于路网饱和度的城市土地混合利用规划[J]. 公路交通科技, 2015, 32(5)： 129-134.

Xie Benyi, Jiang Huiyuan. Urban mixed-land-use planning based on road network saturation[J]. Journal of Highway and Transportation Research and Development, 2015, 32(5)： 129-134. (in Chinese)

[4] 石艳， 范兴华. 长三角地区城市水安全模糊聚类分析[J]. 水电能源科学， 2014, 32(4)： 147-150.

Shi Yan, Fan Xinghua. Fuzzy clustering on urban water security in Yangtze delta[J]. Water Resources and Power, 2014, 32(4)： 147-150. (in Chinese)

[5] Bao Q， Ruan D， Shen Y J, et al. Improved hierarchical fuzzy TOPSIS for road safety performance evaluation [J]. Knowledge-Based Systems, 2012, 32： 84-90.

[6] 党晓旭， 王元庆， 吴洲豪， 等． 区域道路交通安全变化测度研究[J]. 中国安全科学学报， 2015, 25(1)： 152-157.

Dang Xiaoxu, Wang Yuanqing, Wu Zhouhao, et al. Research on variation metric of regional road traffic safety[J]. China Safety Science Journal, 2015, 25(1)： 152-157. (in Chinese)

[7] 张烨， 文竹. 煤炭城市道路规划[J]. 煤炭技术, 2013, 32(4)： 117-118.

Zhang Ye, Wen Zhu. Coal cities urban road planning[J]. Coal Technology, 2013, 32(4)： 117-118. (in Chinese)

[8] 龚鹏飞. 城市道路交通突发事件应急响应分级研究[J]. 现代城市研究, 2015(3)： 23-27.

Gong Pengfei. Classification of emergency response to urban road traffic emergencies[J]. Modern Urban Research, 2015(3)： 23-27. (in Chinese)

[9] 赵学刚. 城市道路交通安全风险分类动态评价技术[J]. 中北大学学报(自然科学版), 2014, 35(4)： 419-426.

Zhao Xuegang. Dynamic evaluation technology about classification of urban road traffic safety risks[J]. Journal of North University of China(Natural Science Edition), 2014, 35(4)： 419-426. (in Chinese)

[10] 劳昕， 沈体雁， 孔赟珑. 中国城市规模分布实证研究——基于微观空间数据和城市聚类算法的探索[J]． 浙江大学学报(人文社会科学版)， 2015, 45(2)： 120-132.

Lao Xin, Shen Tiyan, Kong Yunlong. The empirical research on China’s city size distribution: an exploration based on the micro spatial data and city clustering algorithm[J]. Journal of Zhejiang University(Humanities and Social Sciences), 2015, 45(2)： 120-132. (in Chinese)

[11] 赵学刚. 城市道路交通安全综合风险预警控制研究[J]. 中国安全科学学报, 2016, 26(2)： 158-163.

Zhao Xuegang. Research on integrated warning control of urban traffic safety risks[J]. China Safety Science Journal, 2016, 26(2)： 158-163. (in Chinese)

[12] 杨浩雄, 李金丹, 张浩, 等. 基于系统动力学的城市交通拥堵治理问题研究[J]. 系统工程理论与实践, 2014, 34(8)： 2135-2143.

Yang Haoxiong, Li Jindan, Zhang Hao, et al. Research on the governance of urban traffic jam based on system dynamics[J]. Systems Engineering-Theory & Practice, 2014, 34(8)： 2135-2143. (in Chinese)

[13] 辛督强. 基于熵权-TOPSIS 模型的我国区域道路交通安全评价[J]． 物流技术, 2015, 34(9)： 108-110.

Xin Duqiang. Evaluation of regional highway transportation safety in China based on entropy-TOPSIS model[J]. Logistics Technology, 2015, 34(9)： 108-110. (in Chinese)

[14] 赵学刚， 谭迎新． 区域道路交通事故伤亡风险源分类评价研究[J]．中国安全科学学报， 2013， 23(2)： 160-165.

Zhao Xuegang, Tan Yingxin. Classification evaluation of regional road traffic accident casualty risk sources[J]. China Safety Science Journal, 2013， 23(2)： 160-165. (in Chinese)

[15] 赵学刚. 区域路网交通安全风险动态预警关键技术研究[D]． 西安： 长安大学， 2010.

[16] 蒋辉, 邓伟民, 陈晓青. 基于Pearson系数与多元核支持向量分类的葡萄酒分析[J]. 农业机械学报, 2014, 45(1)： 203-208.

Jiang Hui, Deng Weimin, Chen Xiaoqing. Analysis of wine based on Pearson coefficient and multiple kernel support vector classification[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(1)： 203-208. (in Chinese)

[17] 黄艳国， 许伦辉， 邝先验. 基于模糊C均值聚类的城市道路交通状态判别[J]. 重庆交通大学学报(自然科学版)， 2015, 34(2)： 102-107.

Huang Yanguo， Xu Lunhui， Kuang Xianyan. Urban road traffic state identification based on FuzzyC-mean clustering[J]. Journal of Chongqing Jiaotong Univresity(Natural Science), 2015, 34(2)： 102-107. (in Chinese)

[18] 王承宗. 中部六省金融、 教育与经济增长的比较研究[J]. 统计与决策, 2015, 434(14)： 103-105.

Wang Chengzong. A comarative study of financial education and economic growth in six central provinces[J]. Statistics & Desision, 2015, 434(14)： 103-105. (in Chinese)