基于改进的模糊C均值聚类算法的颗粒种子图像分割方法

王 宇， 陈 婧， 王 高

(1. 山西工程职业技术学院 电气工程系， 山西 太原 030009； 2. 中国航天科工集团第二研究院706所， 北京 100854； 3. 中北大学 仪器科学与动态测试教育部重点实验室， 山西 太原 030051； 4. 中北大学 电子测试技术国防科技重点实验室， 山西 太原 030051)

0 引 言

图像处理技术和机器视觉技术的不断完善使得应用计算机视觉、 图像处理和模式识别来实现农作物颗粒种子检测的自动化成为可能. 机器视觉系统的光电系统能获得被检测对象的图像信号， 利用适当的方式处理图像信息后可通过识别、 分析得到检测结果， 图像信息处理方法的适用与否及处理结果的好坏直接影响到后续图像分析的结果， 因此机器视觉系统能够广泛应用的前提是图像处理工作的精确化[1].

在此背景下， 本文对农作物颗粒种子机器视觉计数检测系统中， 光电采集系统所采集的农作物颗粒种子图像(如图 1 所示玉米种子原始图像)进行图像分割算法的研究， 该工作处于对原输入图像平滑、 去噪处理之后(如图 2 所示玉米种子平滑图)， 支持向量机(SVM)计数工作之前. 为了能够准确地自动计数颗粒， 需要对图像进行有效分割， 避免分割不好造成计数错误.

图 1 玉米种子原始图象Fig.1 Original image of corn seeds

图 2 玉米种子平滑图Fig.2 Image of corn seeds after smooth processing

图像分割是指将图像中具有相似特征的区域进行划分， 且划分后的区域之间存在着差异性. 在对农作物颗粒种子图像进行检测识别、 计数之前要先进行图像分割， 即将每个颗粒种子从图像中独立分割出来， 它决定了后续计数结果的准确性及系统检测的整体速度. 20世纪90年代初主要采用算法相对简单的阈值分割、 边缘检测等图像分割方法， 这些算法对一般图像的错误率较大[2-4]. 2000年后出现的超像素分割方法， 特别是模糊C均值聚类(FCM)算法尽管复杂度较高、 计算量较大， 但分割效果比早期的阈值分割、 边缘检测等方法好[5]. 本文采用改进的FCM算法对颗粒种子图像进行分割， 使单个种子与背景图像分开， 只有当种子与背景明显分离， 单个的种子才具备计数条件.

1 基于聚类的图像分割方法

图像分割是把所有属性相同或相似的像素点划分为同类， 这个过程就是聚类. 只有使同类的特征点密集， 不同类的特征点相距疏远， 聚类方法才是有效的. 由此， 特征点在特征空间中的分布情况决定了基于相似准则建立的聚类方法的有效性.

聚类算法最常用的是K均值(K-means)聚类， 它的优势在于简洁和高效[2-5].

1.1 K-means聚类算法流程

设定输入为有k个聚类的待分类样本集X={x1,x2,x3,…,xn}， 输出为k个聚类Cj(j=1,2，…，k).

1) 初始化： 选取k个初始聚类中心；

2) 分配样本： 按照最小距离原则将每个样本分配到最邻近的聚类中心；

3) 修正聚类中心： 设定每个聚类中的样本均值作为新的聚类中心；

4) 判断是否满足收敛条件： 重复2), 3)步骤， 直到聚类中心变化值小于预设阈值；

5) 结束： 输出k个聚类.

1.2 K-means聚类算法的局限性

K-means聚类图像分割算法属于一种硬聚类分割算法， 即每一个像素点明确只能属于某一类. K-means聚类算法分割图像时有以下明显的局限性：

1) 使用该算法分类之前必须事先给出待分类样本集的聚类数目k， 但实际在分类之前我们并不确定样本中到底有多少个分类， 这就需要加大工作量来确定聚类数目k；

2) 该算法对初始聚类中心值敏感， 对于不同的初始聚类中心值， 可能会导致不同的结果；

3) 该算法最大的缺点是对于噪声和孤立点数据非常敏感， 在K-means聚类算法过程中每次迭代需要重新修正聚类中心， 即将每个聚类中的样本均值作为新的聚类中心， 这样就使得少量的噪声及孤立点就会让样本均值偏离真正的聚类中心；

4) 该算法不适用于大量数据的聚类， 由于K-means聚类算法需要多次迭代来确定最终的聚类结果， 而每次迭代都需要计算所有样本均值， 这就使得计算量过大， 耗时过多.

2 基于FCM的图象分割算法

软聚类分割算法能够更准确地对图像像素进行归类， FCM算法就是其中的一种， 即使在复杂的背景下， 依然能够实现准确的图像分割. 这种算法将样本点属于隶属度类别的程度考虑其中， 而不像K-means聚类算法中只是简单地将其区分为“是”或“不是”， 分割结果比K-means聚类算法更为精确化、 合理化.

2.1 模糊集理论

在集合理论中， 其特征函数为

(1)

从特征函数中可以看出， 这是一个不连续函数， 根据元素的取值区间不同， 相应的函数结果只有“0”和“1”， 但是某一个像素点其实是与周边的像素点存在一定的联系的， 它们并不是孤立存在的， 因此， 这样的特征函数应用在实际分割图形的过程中并不能体现出像素点之间的联系， 只是就点论点， 缺乏客观性， 图形分割结果会有失准确性. 因此， 需要对特征函数进行改进， 将原来离散化的取值改成从0到1的连续区间， 使得利用该函数得到的结果更加合理， 而函数改进的过程也就是用隶属函数取代特征函数的过程.

2.2 FCM图像分割算法

由于FCM算法本身的优势， 使其能够更加精确地处理图像的分割问题， 应用前景非常广泛， 很多国内外的专家学者致力于它的发展研究， 以便更好的应用于实际工作中. 首先提出用模糊理论处理聚类问题的是Zadeh等人， 在此基础上， Ruspini提出了新的聚类方法， 为

(2)

后来， Dunn把聚类的目标函数改进为类内加权误差平方和形式， 目标函数表示为

(3)

随着研究的不断深入， 为了让该理论能够解决更多的实际问题， 在原来的基础上， BezDek将模糊加权指数m引入到目标函数中， 使模糊目标函数进一步一般化，

(4)

隶属度函数uik表示第k个样本xk属于第i个聚类中心vi的程度，uik∈[0,1]. 模糊聚类的划分矩阵均属于以下划分空间，

m∈[1,∞]为模糊加权指数， 控制着样本在各个类间的分享程度， 有相关的研究表明，m的最佳取值范围为[1.5,2.5][6].

引入拉格朗日乘子λ求解， 并使目标函数Jm最小，

(6)

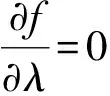
(7)

式中：dik=‖xk-vi‖.

FCM算法流程：

1) 初始化：V0为聚类中心，b为迭代次数(b的初始值为0)，c为聚类个数(2≤c≤n)，ε为迭代阈值(ε>0)[4]；

2) 划分矩阵的更新： 计算模糊聚类的划分矩阵Ub；

3) 更新聚类中心： 根据式(8)更新聚类中心Vb+1；

4) 输出： 如果‖V(b+1)-V(b)‖<ε则停止迭代， 将U,V输出， 反之则继续执行第2)步[7-9]；

5) 去模糊化： 即某一样本点属于哪个类别的程度最大， 则判定该样本点属于哪一类， 用Ck表示第k个样本点所属的类别， 有Ck=argimax(uik),∀i,∀k.

图 3 为玉米种子图像使用传统FCM算法分割的结果， 可以看到： 大部分种子实现了边界清晰地分割， 但个别种子之间存在明显的粘连， 这就使得后续的计数产生误差， 这是传统FCM算法存在的局限性.

图 3 传统FCM算法分割结果Fig.3 Segmentation result by traditional FCM algorithm

3 改进的FCM图像分割算法

3.1 传统FCM算法的缺陷

传统FCM算法存在的主要缺陷有：

1) 在图像分割的过程中， 某一点的像素值并不是孤立的， 它与周边相邻的像素值之间存在着联系. 但是传统FCM算法并没有考虑某像素与它相邻的像素值之间的影响而只考虑单一像素， 即没有考虑图像的空间信息. 当图像受到噪声影响时， 传统FCM算法使得图像的分割不充分而导致像素点的错误分类， 得不到满意的分割结果[7-10].

2) 传统FCM聚类算法没有考虑像素点属于该聚类的程度对最终模糊聚类目标函数的影响， 使得每一个像素点都是孤立的， 这样会增加分割过程中对干扰因素的敏感性， 使得最终得出的图像分割结果并不精确[11-12].

3.2 传统FCM算法的改进

针对上述的缺陷1)， 在传统FCM算法的目标函数中加入惩罚项来说明邻域像素值的影响. 带惩罚项的非线性目标函数可以表示为

(9)

式中：ξ为惩罚项； ∂为惩罚项的系数. 在图像分割的过程中， 惩罚项的存在可以对空间信息进行有效的约束， 它可以提升像素聚类的准确性， 尤其当图像受到噪声影响时， 惩罚项起到的作用会更加明显， 它可以削弱甚至消除噪声对像素正确聚类的干扰.

具体改进后的FCM算法目标函数为

对目标函数引入模糊加权因子来改进上述传统FCM算法的缺陷2)， 这样在FCM聚类算法的基础上既判定了每一个像素点xk对于不同聚类中心的隶属程度， 又判定了不同的像素点对于同一个聚类中心的隶属程度. 模糊加权因子的性质类似于隶属度， 但作用不同于隶属度函数uik. 其定义为

(11)

式中：Wik为第k个样本点属于第i个聚类中心的模糊加权因子.

3.3 改进后的FCM算法

以下为改进后的目标函数

式中：xk距离聚类中心越远，Wik越大， 1/Wik越小， 距离放大的尺度就越小， 所以距离值越小.

实际上模糊加权距离的原理就是用加权因子来修饰空间距离， 在这个过程中它利用倒数来使聚类更加准确， 并且使聚类结果更加合理[13-16]. 将空间距离取倒数， 这样像素点的距离越大， 即放大的尺度越大， 反之， 则尺度越小， 最终导致“两级分化”使得图像更易于聚类， 而得到很好的聚类结果.

图 4 为玉米种子图像使用改进的FCM聚类算法分割的结果. 由图4可以看到： 目标与背景分割明确， 种子之间的粘连明显减少， 为后续种子计数打下很好的基础.

图 4 改进的FCM分割结果Fig.4 Segmentation result by improved FCM algorithm

4 实验结果分析

实验选取玉米种子作为样本， 采用大恒水星MER-500-7UM工业数字摄像机及百万像素系列变焦镜头M3Z1228C-MP采集图像， 检测系统软件使用Qt Creator制作界面， 程序编写使用C++， 使用OpenCV图像处理库来进行种子图像平滑处理、 图像分割以及后续的计数功能， 如图 5 所示为采用改进FCM分割方法后进行种子计数的软件运行结果.

图 5 种子计数软件运行结果Fig.5 Result of seed count testing software

选取5张玉米种子图像作为本次实验的输入样本图像， 其中3张样本的颗粒数相同， 其余2张样本的颗粒数不同. 对上述5张图像分别进行两次实验， 两次实验的图像平滑处理都采用中值滤波， 计数方法都采用支持向量机(SVM)， 而图像分割分别采用传统FCM算法与文中改进的FCM算法. 对这5张图像最终的计数结果、 准确率、 检测耗时进行比较分析， 表 1 为传统FCM算法的实验结果数据， 表 2 为改进FCM算法的实验结果数据.

从两组实验结果看到， 改进的FCM算法相对于传统的FCM算法考虑了像素的空间邻域信息以及同一类别不同像素的归属程度， 这就使得改进的FCM聚类算法具有更强的抗噪声性能， 准确率平均可以达到99%， 比传统的FCM算法高出6%， 少数情况下有一定的误差， 而误差的存在主要是由于种子分布上存在重叠， 造成计数误差.

表 1 传统FCM算法的实验结果

表 2 改进FCM算法的实验结果

在处理速度上， 由于改进的FCM算法采用模糊加权因子对目标函数进行改进， 减少了聚类过程的迭代次数， 计算时间仅为传统FCM算法的一半， 使整个检测系统的效率得到提高.

通过实验验证了整个改进过程的有效性和合理性， 图像分割结果更加精确、 高效， 图像分割工作得到进一步完善和质量的进一步提升， 为下一步准确计数打下良好基础.

5 结 论

本文在介绍了K-means、 FCM算法之后， 针对两种算法在应用中的特点， 提出了K-means、 FCM算法在类似种子图像分割中的不足之处. 使用K-means算法， 首先要加大工作量来确定聚类数目k； 其次其对初始聚类中心值、 噪声和孤立点数据敏感； 并且在修正聚类中心的过程中会让样本均值偏离真正的聚类中心； 而且该方法不适用于大量数据的聚类. 而FCM算法虽然在K-means算法上进行了改进， 但是由于它没有考虑图像的空间信息， 当图像受到噪声影响时， 会导致像素点的错误分类； 且FCM算法没有引入像素点隶属度对其最终模糊聚类目标函数的影响， 使得最终结果有失客观性. 而改进后的FCM算法考虑了像素的邻域信息并引入像素点隶属于最终聚类的程度， 使得分割更具有科学性和合理性. 最后用机器视觉系统获取的种子图像对传统FCM算法及改进的FCM算法进行了分割后的计数实验验证， 结果同样表明改进的FCM算法在准确率及处理速度上都较传统FCM算法有优越性， 改进的算法在颗粒种子机器视觉检测中能够得到很好的应用.

参考文献：

[1] 杨淑莹. 模式识别与智能计算[M]. 北京： 电子工业出版社, 2011.

[2] 章毓晋. 图像分割[M]. 北京： 科学出版社， 2001.

[3] 王威, 曾小能. 图像分割技术研究与应用[J]. 计算机时代， 2015(1)： 26-28.

Wang Wei， Zeng Xiaoneng. Research of image segmentation technology and application[J]. Computer Era， 2015(1)： 26-28. (in Chinese)

[4] 张丹丹， 赵双. 图像分割技术综述[J]. 科技创新与应用， 2013(10)： 36.

Zhang Dandan， Zhao Shuang. Review of image segmentation technology[J]. Technology Innovation and Application， 2013(10)： 36. (in Chinese)

[5] 汪梅， 何高明， 贺杰. 常见图像分割的技术分析与比较[J]. 计算机光盘软件与应用， 2013， 16(6)： 63-64.

Wang Mei， He Gaoming， He Jie. Analysis and comparison of common image segmentation technical [J]. Computer CD Software and Applications， 2013， 16(6)： 63-64. (in Chinese)

[6] 高新波， 谢维信. 模糊c-均值聚类算法中加权指数m的研究[J]. 电子学报， 2000， 28(4)： 80-83.

Gao Xinbo， Xie Weixin. A study of weighting exponent m in a fuzzy C-means algorithm[J]. Acta Electronica Sinica， 2000， 28(4)： 80-83. (in Chinese)

[7] Pal N R， Bezdek J C. On cluster validity for the fuzzy c-means model[J]. IEEE Transactions on Fuzzy Systems， 1995， 3(3)： 370-379.

[8] 张洪艳. 模糊C均值聚类算法及应用[J]. 科技资讯， 2014(5)： 178-179.

Zhang Hongyan. Fuzzy c-means clustering algorithm and its application[J]. Science & Technology Information， 2014(5)： 178-179. (in Chinese)

[9] Ambroise C， Govaert G. Convergence of an EM-type algorithm for spatial clustering[J]. Pattern Recognition Letters， 1998， 19(10)： 919-927.

[10] Ayech M W， El Kalti K， El Ayeb B. Image segmentation based on adaptive fuzzy-C-means clustering[J]. International Conference on Pattern Recognition (ICPR)， 2010， 12(10)： 2306-2309.

[11] 王颖洁， 白凤波， 王金慧. 关于模糊C-均值(FCM)聚类算法的改进[J]. 大连大学学报， 2010， 31(6)： 1-4.

Wang Yingjie， Bai Fengbo， Wang Jinhui. Improvement of the fuzzy C-means clustering algorithm[J]. Journal of Dalian University， 2010， 31(6)： 1-4. (in Chinese)

[12] Yang Y， Zheng C X， Lin P， et al. A new algorithm for image segmentation based on modified fuzzy C-means clustering[J]. Journal of Optoelectronicslaser， 2005， 16(9)： 1118-1122.

[13] Pu P B, Wang G, Liu T A. Research of improved fuzzy C-means algorithm based on particle swarm optimization[J]. Computer Engineering and Design， 2008， 10(6)： 556-675.

[14] Wang G H， Li D H. A fast and effective fuzzy clustering algorithm for color image segmentation[J]. Journal of Beijing Institute of Technology， 2012， 21(4)： 518-525.

[15] Li Y L， Sheng Y. Fuzzy C-means clustering based on spatial neighborhood information for image segmentation[J]. Journal of Systems Engineering and Electronics， 2010， 21(2)： 323-328.

[16] Lou X J， Li J Y, Liu H T. Improved fuzzy C-means clustering algorithm based on cluster density[J]. Journal of Computational Information Systems， 2012， 8(2)： 727-737.