旋转直接驱动电液压力伺服阀稳定性分析
原佳阳, 訚耀保, 陆 亮, 方 向, 夏飞燕
(1. 同济大学 机械与能源工程学院,上海 200092;2. 南京机电液压工程研究中心,江苏 南京 210061;3. 航空机电系统综合航空科技重点实验室,江苏 南京 210061)
上世纪90年代前后,出现了旋转直接驱动电液伺服阀(RDDV)的新结构[1].这种伺服阀通过旋转驱动机构,将力矩马达旋转运动转化为功率滑阀直线运动;由于取消了传统伺服阀的前置液压放大级、加入电反馈伺服控制,这种直接驱动式伺服阀具有结构简单、可靠性高、抗污染能力强,控制方式灵活的优点;且由于马达转动和滑阀平动方向垂直,旋转直驱式伺服阀在结构布置上相对于直线直驱阀更加紧凑[2],在国外已逐渐应用于飞机电子防滑刹车、飞行器舵面及发动机控制等领域[3].
电液伺服阀是电液伺服控制系统的核心元件,其性能对系统乃至整机的工作特性有决定性的影响[4];并且电液伺服阀作为机电液综合的精密控制元件,其中的能量转换过程多、参数匹配关系较为复杂[5];因此电液伺服阀稳定性和快速响应性能的分析和改进一直是国内外的热点研究方向.国外方面,Watton深入研究了喷嘴挡板式放大器产生啸叫的原因,并提出调整回油阻尼元件参数的方法降低振动啸叫[6].Ziada等对水轮机控制阀的啸叫现象进行了分析,认为剪切层振荡造成了阀内的流体压力脉动[7].此外,文献[8-9]分别研究了气穴和回油压力波动对伺服阀稳定工作的影响.Klarecki分析了电子控制器参数对电液伺服系统动态特性的影响[10].国内方面,李松晶等人研究了力矩马达的振动啸叫情况,通过向工作间隙加入磁流体的方法,抑制了力矩马达的自激振动[11].南京机电液压工程研究中心针对偏导板式放大器的啸叫进行了仿真和试验对比研究,通过改变结构参数,消除了前置级流场的卡门涡,改善了伺服阀的啸叫问题[12].压力伺服阀由于输出增益大,其振动和失稳问题更加突出[13],但目前对压力伺服阀动态特性研究的文献较少.
在研制某旋转直接驱动电液压力伺服阀(RDDPV)过程中,发现其稳定性差,工作过程中出现控制压力大幅振荡的现象,本文建立了该阀的非线性数学模型及简化框图,进行了整阀的稳定性分析,得到了保证伺服阀稳定工作的结构参数设计依据和控制参数调试方法,提出了提高RDDPV稳定性的具体措施,并进行了试验验证.
1 RDDPV工作原理及数学模型
1.1 RDDPV工作原理
旋转直接驱动电液压力伺服阀工作原理如图1

1—电子控制器;2—转角位移传感器;3—有限转角力矩马达;4—偏心驱动机构;5—回油单向阀;6—功率滑阀;7—偏置弹簧;8—阀套;9—阀体;10—压力传感器;11—负载容腔;12—溢流阀;13—液压泵;14—油箱
图1旋转直接驱动电液压力伺服阀工作原理
Fig.1Operationprincipleofrotarydirectdriveelectrohydraulicpressurecontrolservovalve
所示,主要由电子控制器、有限转角力矩马达、偏心驱动机构、功率滑阀副和相关传感器组成.当电子控制器输入指令为0时,转角力矩马达无力矩输出,此时滑阀被复位弹簧推至最右端,进油口关闭,工作腔与回油口接通,伺服阀输出压力为零;当输入非零正指令信号i0时,电子控制器经过计算,输出PWM信号驱动转角力矩马达旋转,偏心驱动机构将马达的旋转运动转化为功率阀芯的直线运动;功率滑阀为负遮盖形式,阀芯的直线运动改变了进回油口节流面积比;Pc口所接的负载容腔在刹车时为闭死容腔,因此负载容腔的稳态压力值仅随进回油口节流面比变化;阀芯的有效行程即为负遮盖量.该阀采用电反馈形式进行伺服控制;转角位移传感器将力矩马达旋转角度反馈至控制器,形成马达位置内闭环;压力传感器将工作腔压力反馈,形成压力外闭环控制.
马达转轴末端偏心驱动机构初始状态示意图见图2.图中小球和柱形孔具有相同的名义尺寸,坐标原点O为滑阀中心轴线和柱形孔中心轴线的交点,X轴过O点平行于滑阀中心轴线,Y轴过O点平行于马达转轴;通过结构和尺寸调整保证马达转轴处于YZ平面上,且小球球心距离XOZ平面高度为h.
初始状态时,柱形孔中心轴线与Y轴重合;当马达转动,小球球心绕马达转轴旋转,可分解为X和Z方向运动;其中小球X方向的运动带动阀芯平动,从而改变进回油口节流面积;而Z方向的运动则带动阀芯绕X轴转动.

图2 马达转轴末端偏心驱动机构初始状态示意图Fig.2 Sketch of initial status of the eccentric drivemechanism on the end of the motor shaft
1.2 RDDPV数学模型
1.2.1马达及功率阀芯动力学方程
马达转子受到的电磁驱动力矩Tem为
Tem=kti0-kmα2
(1)
式中:i0为马达输入电流;α为马达转子转动角度;kt为电流力矩系数;km为转角力矩系数.
马达转子的动力学方程为
(2)
式中:Tf为负载力矩;Jr为马达转子的转动惯量;Br为马达转子的阻尼系数.
滑阀在打开过程中,存在两个方向的运动:沿滑阀轴向的平动和绕滑阀中心轴线的转动,将两个方向的运动分解,有

(3)
Fs=2CdπDvcosφ[xv(Ps-Pc)-(U-xv)Pc]
(4)

(5)
式中:Fx为滑阀轴向平动的驱动力;Tβv为滑阀转动的驱动力矩;Fs为稳态液动力;xv为滑阀位移;Cd为滑阀阀口流量系数;mv为阀芯质量;Dv为阀芯端面直径;Bv为滑阀轴向平动阻尼系数;kv为偏置弹簧刚度;xv0为偏置弹簧预压缩量;φ为滑阀节流口射流角;βv为阀芯绕阀芯轴线的转角;Jβv为滑阀对其中心轴线的转动惯量;Bβv为滑阀转动阻尼系数;U为滑阀预开口量;Ps为供油压力;Pc为工作腔压力.
1.2.2偏心机构运动学及力学方程
图3为偏心驱动机构运动和力传递三维示意图.

图3 偏心驱动机构运动和力传递三维示意图Fig.3 Diagram of motion and force transfer processof the eccentric drive mechanism
根据图中几何关系可求得阀芯运动(沿X轴位移xv和绕X轴转动角度βv)与马达转角α间的运动学表达式为
xv=esinα
(6)
图中小球受到阀芯作用力为Fxb(为滑阀轴向驱动力Fx的反作用力)和Fβvb(为滑阀绕轴向转动驱动力的反作用力),有
Fxb=Fx
Tf=Fxbecosα+Fβvbesinαcosβv
(7)
1.2.3负载压力方程
压力伺服阀应用于飞机刹车系统时,其控制的刹车作动筒行程极小;因此,在刹车用压力伺服阀的试验和理论分析中,通常采用固定容积的容腔代替实际刹车腔,油液连续性方程为
(8)
式中:ρ为油液密度;V为负载腔容积;E为油液体积弹性模量.
1.2.4电子控制部分
如图4所示,为电子控制部分示意图.
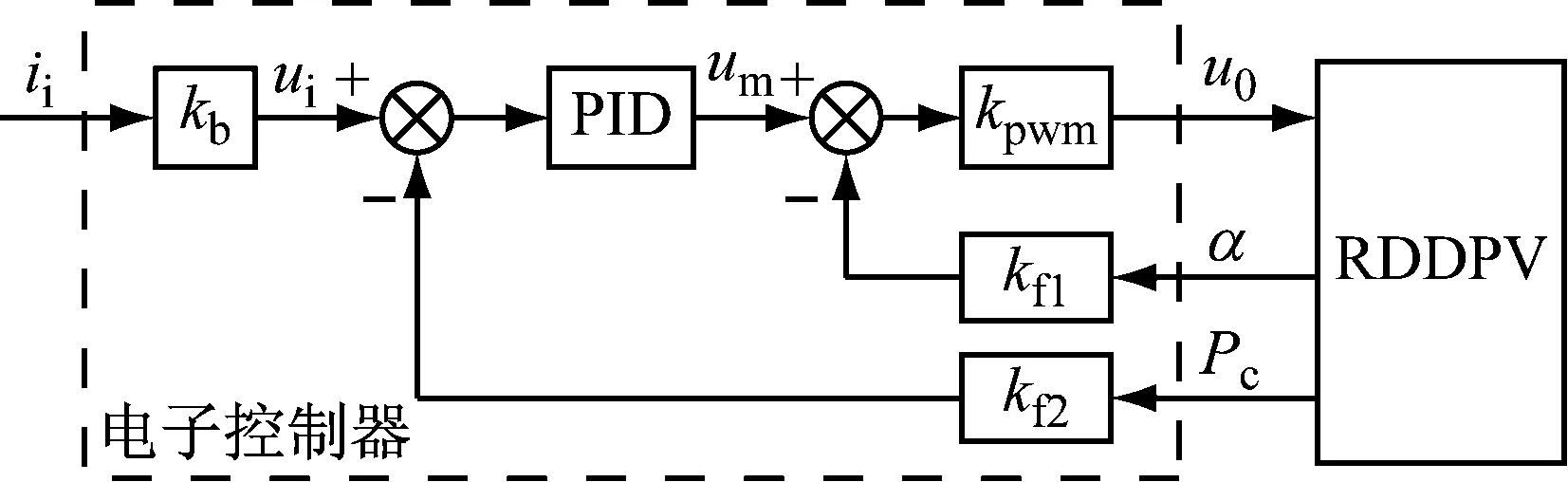
图4 电子控制部分示意图Fig.4 Diagram of electronic controller
电子控制器实现的主要功能有
(1)信号调理;将输入的控制电流信号ii转化为电压信号ui,并进行降噪滤波处理;该环节为比例环节,比例系数为kb;
(2)压力外闭环的PID控制;压力传感器(响应频率>1 kHz,视为比例环节)将液压力Pc转换为相应电压,该电压信号经放大器线性放大后作为压力反馈信号up,这一过程的比例系数为kf2(即,up=Pckf2),称为负载压力电反馈系数;根据输入信号ui和压力反馈信号up的差值进行比例、积分和微分运算,得到压力反馈控制的输出信号um;
(3)马达转角反馈控制:旋转变压式角位移传感器(响应频率>1 kHz,视为比例环节)将马达转角α转换为相应电压,该电压信号经放大器线性放大后作为马达转角反馈信号uα,这一过程的比例系数为kf1(即,uα=αkf1),称为马达转角电反馈系数;压力反馈控制的输出信号um与马达转角反馈信号uα作差,输出最终的马达控制信号.
(4)PWM放大:将控制信号进行功率放大,输出驱动马达运动的电压信号u0.该环节为比例环节,比例系数为kpwm.因此,电子控制部分的数学模型为
ui=kbii
u0=(um-αkf1)kpwm
(9)
式中,s为Laplace算子.
2 RDDPV稳定性分析
2.1 RDDPV线性化数学模型
式(1)中的转角力矩系数较小,可忽略,有
Tem=kti0
(10)
由于压力伺服阀阀芯位移小,所需的马达转动角度α也较小(<6°),式(6)可以简化为
xv=eα
(11)
式中:αx为马达转子的任意工作点.
式(8)为控制压力方程,在滑阀任意工作点xvx(xvx=eαx)附近线性化可得
Pc=kpxv
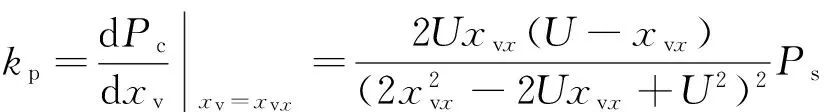
(12)
式中:kp为滑阀在工作点xvx的压力增益.作用在滑阀上的稳态液动力视为弹性力,有
Fs=ksxv
ks=2CdπDvcosφ(Ps-Ukp)
(13)
式中:ks为滑阀在工作点xvx的稳态液动力刚度.
将式(7)、(11)和(13)代入式(2),可得马达转子在工作点αx的动力学方程
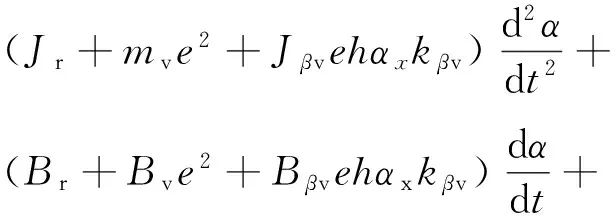
(kv+ks)e2α+kvexv0
(14)
根据式(2)和(9)—(14)得到如图5所示的RDDPV在任意工作点线性化框图.图中JM、BM、KM分别为伺服阀中机械运动部件等效到马达转轴上的转动惯量、阻尼系数和弹性系数,根据式(14)有
JM=Jr+mve2+Jβvehαxkβv
BM=Br+Bve2+Bβvehαxkβv
KM=(kv+ks)e2
(15)

图5 RDDPV在任意工作点线性化框图Fig.5 Block diagram of RDDPV after linearization at arbitrary operating point
2.2 结构及控制参数对RDDPV稳定性的影响
根据图5的RDDPV框图,可得到传递函数为
(16)

根据劳斯稳定性判据,伺服阀保持稳定的充要条件为a1a2>a0a3;带入可得任意工作点αx附近的RDDPV稳定性判据[15]
(17)
式中:KEα为马达转角电反馈刚度;KEp为供油压力电反馈刚度;B为整阀阻尼.有
(18)
式(17)中,RDDPV机械部分刚度KM主要由稳态液动力刚度和复位弹簧刚度组成,其中复位弹簧是为保障掉电状态下阀芯复位而设计的,为减小阀芯开启的阻力,复位弹簧刚度kv取值较小,设计中取kv为2~6 N·mm-1.工作点xv对稳态液动力Fs和稳态液动力刚度ks的影响如图6所示;可见,相比稳态液动力刚度ks,复位弹簧刚度kv在RDDPV机械刚度KM中所占比重较小.

(U=0.1 mm,Dv=6 mm,Ps=8 MPa)图6 工作点xv对稳态液动力Fs和稳态液动力刚度ks的影响
Fig.6Effectofoperatingpointxvonthesteady-stateflowforceFsandrigidityofsteady-stateflowforceks
图6中,当滑阀阀芯位于进回油口中间位置(xv=U/2)附近时,稳态液动力的刚度ks为负向最大值,在滑阀开启过程中表现为正反馈作用,不利于伺服阀稳定;若此时电反馈刚度(KEα、KEp)较小,RDDPV参数不满足式(17)所示判据,伺服阀将处于失稳状态.因此,根据式(17)所示的稳定性判据,为使RDDPV能够在所有工作点稳定工作,需要保证足够大的电反馈刚度.
3 理论及试验结果分析
根据式(17)所示,增加RDDPV电反馈刚度的方法有:提供较大的马达转角电反馈刚度KEα、较大的供油压力电反馈刚度KEp或将PID控制器的比例系数KP调大等.为了进一步说明内位置闭环对直接驱动式压力伺服阀的重要作用,本文将重点介绍马达转角电反馈刚度KEα对RDDPV稳定性的影响.根据式(18),通过增加马达转角电反馈系数kf1可达到增加转角电反馈刚度KEα的目的.
3.1 RDDPV数值模拟
RDDPV主要结构参数如表1所示.采用Runge-Kutta算法对式(1)—式(9)的非线性数学模型求解,可得到RDDPV的数值模拟结果.
供油压力8 MPa时,输入频率0.05 Hz,幅值7.5 mA的三角波信号作为指令,可得到如图7所示的RDDPV压力特性理论曲线,图7a为马达转角电反馈系数kf1取0.2 V·deg-1时对应的理论压力特性曲线;从图中可以看出,指令电流增加时(0→7.5 mA),RDDPV在5→6.5 mA的工作点输出压力抖动;指令电流减小时(7.5 mA→0),RDDPV在4.5→3 mA的工作点处有压力抖动现象.指令电流增加和减小时负载压力波动对应的工作点不同,这是由于机械结构在稳定状态和失稳状态转化的过程中对应着能量的积累和散耗,而能量的变化需要时间,因此形成了如图7a中所示的“迟滞”现象.但“去程”和“回程”时,失稳初始发生的工作点是相近的(4.8 mA左右),即滑阀阀芯工作行程的中间位置(xv=U/2).图7b为马达转角电反馈系数kf1取0.4 V·deg-1时对应的理论压力特性曲线.可以看出,电反馈刚度的提高,提升了RDDPV整阀刚度及稳定性,伺服阀输出的负载压力无抖动.

表1 RDDPV主要结构参数Tab.1 Main structural parameters of RDDPV

a马达转角电反馈系数kf1=0.2V·deg-1b马达转角电反馈系数kf1=0.4V·deg-1
(kf2=0.4 V·MPa-1,KP=1.2,KI=70)
图7RDDPV压力特性理论曲线
Fig.7TheoreticalcurveofRDDPVpressurecharacteristics
3.2 RDDPV试验结果及其分析
对所研究的RDDPV进行压力特性测试,所用的压力伺服阀试验台工作介质为15号航空液压油,供油压力8 MPa.试验中,通过改变相应放大器放大倍数的方法,调节马达转角电反馈系数kf1.
输入频率0.05 Hz,幅值7.5 mA的三角波信号,可得到如图8所示的RDDPV压力特性试验曲线.当马达转角电反馈系数kf1取0.2 V·deg-1时,试验过程中,RDDPV输出压力也存在抖动现象;且试验得到的压力抖动工作点与理论相对应.试验得到的负载压力波动频率和幅值小于理论值,是由于数学模型所选取的非线性摩擦力、阻尼系数等有利于阀芯稳定的软参量与实际情况有偏差而造成的.而当马达转角电反馈系数kf1取0.4 V·deg-1时,RDDPV整阀刚度提升,伺服阀可输出稳定的控制压力.

a马达转角电反馈系数kf1=0.2V·deg-1b马达转角电反馈系数kf1=0.4V·deg-1
(kf2=0.4 V·MPa-1,KP=1.2,KI=70)
图8RDDPV压力特性试验曲线
Fig.8TestcurveofRDDPVpressurecharacteristics
4 结论
本文建立了RDDPV数学模型,得到了线性化框图和RDDPV稳定性判据.所研究RDDPV取消了传统压力伺服阀的机械和液压反馈,采用马达转角和输出压力的电反馈伺服控制.当阀芯位于进回油口中间位置附近,稳态液动力表现为阀芯位移的正反馈作用,导致RDDPV的机械液压部分刚度为负,伺服阀稳定性差.为使RDDPV稳定工作,需要提供足够大的电反馈刚度.
数值模拟和试验结果表明,当电反馈刚度较小时,伺服阀失稳,控制压力抖动,而提高马达转角电反馈系数可增加伺服阀电反馈刚度,使伺服阀在所有工作点可输出稳定的控制压力.该结论也说明,内位置闭环对压力伺服阀的稳定工作有重要作用.
参考文献:
[1] VANDERLAAN R D, MEULENDYK J W. Direct drive valve-ball drive mechanism: US Patent 4,672,992[P]. 1987-6-16.
[2] 王海玲.某型旋转直接驱动式伺服阀的研制[J].机床与液压,2015,43(22):81.
WANG Hailing. Research on a direct-drive electro-hydraulic servo valve[J]. Machine Tool & Hydraulics, 2015, 43(22):81.
[3] CHARRIER J J, KULSHRESHTHA A. Electric actuation for flight & engine control system: evolution, current trends & future challenges[C]//45th AIAA Aerospace Sciences Meeting and Exhibit. Nevada: 2007:1391-1396.
[4] ALLE N, HIREMATH S S, MAKARAM S,etal. Review on electro hydrostatic actuator for flight control[J]. International Journal of Fluid Power, 2016, 17(2): 125.
[5] 訚耀保.极端环境下的电液伺服控制理论及应用技术[M].上海:上海科学技术出版社,2012.
YIN Yaobao.Electro-hydraulic servo control theory and application technology under extreme environment [M].Shanghai: Shanghai Science and Technology Press, 2012.
[6] WATTON J. The effect of drain orifice damping on the performance characteristics of a servo valve flapper/nozzle stage [J]. Journal of Dynamic Systems, Measurement, and Control, 1987, 109(1): 19.
[7] ALY K, ZIADA S. Review of flow-excited resonance of acoustic trapped modes in ducted shallow cavities[J]. Journal of Pressure Vessel Technology, 2016, 138(4): 040803.

[9] GHASEMI E, JAZAYERI S A, MOOSAVIAN S A A. Model improvement for a servovalve with force feedback and back pressure[C]//Robotics Automation and Mechatronics, 2008 IEEE Conference. Chengdu: IEEE, 2008: 895-900.
[10] HAN H, LI S, GUO L, ET AL. Numerical investigation on suppressing high frequency self-excited noises of armature assembly in a torque motor using ferrofluid[J]. Shock and Vibration, 2017,2017: 1.
[11] 陈元章.基于CFD的伺服阀衔铁组件啸叫分析[J].机床与液压,2013,41(5):70.
CHEN Yuanzhang. Analysis on whistling of the armature component of servo valve based on CFD[J]. Machine Tool & Hydraulics,2013, 41(5): 70.

[13] JELALI M, KROLL A. Hydraulic servo-systems: modelling, identification and control[M]. New York: Springer Science & Business Media, 2012.
[14] 訚耀保, 原佳阳, 傅俊勇. 先导阀前腔串加阻尼孔的新型双级溢流阀特性分析[J].吉林大学学报(工学版), 2017,47(1):129.
YIN Yaobao, YUAN Jiayang, FU Junyong. Characteristics of two-stage relief valve with a series damping orifice in pilot valve front chamber[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(1):129.
[15] BOLIN C, ENGEDA A. Analysis of flow-induced instability in a redesigned steam control valve[J]. Applied Thermal Engineering, 2015, 83: 40.

