右转圆曲线处避险车道流出角度与引道长度
宋灿灿, 郭忠印, 方 勇
(同济大学 道路与交通工程教育部重点实验室, 上海 201804)
紧急避险车道在我国应用广泛,但由于缺乏相应的标准规范,设置现状堪忧.加之紧急避险车道一般设置于地形条件恶劣的长大纵坡路段,难免将紧急避险车道设置于平面线形条件差的路段.尽管国内外学者均提出紧急避险车道的设置位置需考虑平曲线的影响,但并未形成定量的研究结论[1-3].邓亚娟等通过ADAMS/Car分析了紧急避险车道设置于直线、左转与右转圆曲线时流出角的计算方法,建议避险车道与平曲线相切,但并未给出平曲线半径的范围[4].牛建峰等通过车辆行驶的横向稳定性模型计算了紧急避险车道设置于右转圆曲线的流出角,圆曲线半径高于551 m时,流出角不高于5°[5].
通过对国内既有109条紧急避险车道的设置位置调研发现,设置于直线的比例仅为30%,设置于曲线的紧急避险车道中,左转与右转曲线的比例相当.设置于半径不超过1 000 m的避险车道比例为35%,半径不超过500 m的比例为19%.而引道长度、流出角度与圆曲线半径呈反比关系,与驾驶员客观行车规律相悖.仅2处避险车道的引道长度高于305 m,43%的引道长度满足3 s设计行程.流出角10°以内的比例为48.7%.
AASHTO提出引道长度不低于305 m,流出角度不超过5°[6],国内学者提出9 s[7]和3 s[8-9]设计行程长度为引道长度,流出角度5°为宜[10].纵观国内外现有研究,在提出引道与流出角度的设置阈值时,未考虑主线平面线形对设置值的影响,同时也未考虑引道与流出角度之间的相互影响.
综上,设置于平曲线的紧急避险车道客观存在且数量较大,但现有研究缺乏.同时,缺乏对流出角与引道长度相互影响的研究,因此,本文采用驾驶仿真技术,研究设置于右转圆曲线的紧急避险车道流出角与引道长度.
1 实验方案
1.1 实验变量
根据研究目的,实验变量有右转圆曲线半径、引道长度、流出角度、驶入速度.将公路工程技术标准(JTG B01-2014)[11]中设计速度80 km·h-1的高速公路一般最小圆曲线半径400m作为实验的最小值,将公路项目安全性评价规范(JTG B05-2015)[12]中直线与平曲线的分界标准1 000 m作为最大值,变化梯度为100 m.
既有紧急避险车道流出角的范围为[0°, 45°],通过前期实验,流出角高于40°时车辆成功驶入紧急避险车道的概率急剧下降[13],因此,流出角度的设置值为5°、10°、15°、20°、25°和30°.
本文通过失控车辆驾驶员在足够长的引道内调整车辆行驶方向需要的长度进行引道设置阈值的研究,引道长度取500 m.
AASHTO规定驶入避险车道的设计车速的最小值为129 km·h-1,推荐使用145 km·h-1[6];中国多起长下坡路段交通事故调查分析,事故车辆的运行速度介于95~120 km·h-1之间[14-15].《新理念公路设计指南》建议的驶入车速为100 km·h-1和110 km·h-1[16].综合以上分析,驶入速度取90 km·h-1、100 km·h-1、110 km·h-1和120 km·h-1.
1.2 实验模型
仿真实验路主线长4 km,平曲线半径的转角为30°,并设置对应的超高.圆曲线的曲中点距离起点的距离为3.2~3.5 km之间,紧急避险车道设置于曲中点处.仿真模型纵坡-2%.采用宽24.5 m的标准横断面,并设置2%的双向横坡.主线上标志标线按照路段上实际设置情况设计,紧急避险车道前2 km、1 km和500 m处设置警告标志.
紧急避险车道的制动床长250 m,制动床纵坡8%,制动床宽度为9 m,服务车道宽度3.2 m.渐变段与主线纵坡一致,引导段纵坡与制动床纵坡一致,竖曲线半径600 m,如图1所示.

图1 紧急避险车道平面设置图Fig.1 Horizontal layout of truck escape ramp
1.3 实验驾驶员
参与实验的人员均为拥有B驾照的男性驾驶员,累计参与实验人员16人,年龄范围为28~42岁(平均年龄34.0岁,标准差7.87岁),驾龄范围为5~16年(平均驾龄6.54年,标准差为4.32).
1.4 实验设备
采用日本Forum 8公司开发的UCWin Road Ver.9驾驶模拟平台,可对地形、道路构造、交通流与自然环境模拟,采集数据量大.
1.5 实验流程
驾驶员首先驾驶模拟器自带场景20 km后驾驶试验场景.试验车型为6轴半挂车,驾驶员启动车辆并加速至要求车速后匀速行驶,最后驶入紧急避险车道,并在车辆调整为驾驶员认为可顺利驶入制动床的方位或至制动床时停止方向调整.
2 基于拟合回归的单指标分析
紧急避险车道设置于右转圆曲线时,失控车辆从主线右侧驶出主线并右转驶入紧急避险车道.若紧急避险车道的流出角过大,必然导致车辆驶入紧急避险车道的转向过程存在横向行驶不稳定的风险、车辆碰撞护栏的形式风险、驾驶员心理负荷过高的风险.采用方向调整时间、最小转向半径、方向盘转角幅值、方向盘转角频率4个指标对失控车辆驶入紧急避险车道的风险进行分析.
2.1 方向调整时间
方向调整时间与驶入速度不相关,根据设置的实验变量,流出角度、平曲线半径可能对方向调整时间产生影响,其高程图如图2所示.

图2 不同半径与流出角度下方向调整时间Fig.2 Adjusting time under different horizontalradius and departure angle
方向调整时间呈倒钟型变化,除半径1 000 m、流出角5°的水平外,方向调整时间均大于6 s.流出角相同,方向调整时间随半径的增大呈先增大后减小的变化规律,转折点半径700 m.半径相同,方向调整时间随流出角增大而增大.
方向调整时间与流出角的线性拟合结果如图3和表1所示.

图3 方向调整时间与流出角的线性回归Fig.3 Regression relationship between adjustingtime and departure angle
方差分析的P值均小于0.05的显著性水平,说明流出角对方向调整时间存在显著影响.
同一半径,方向调整时间与流出角呈线性关系,相关指数接近1.回归直线的截距为流出角0°时对应的方向调整时间,定义为切线调整时间.该值随半径的增大呈梯形变化.半径400~800 m时,切线调整时间稳定为8.5 s.半径800~1 000 m时,半径每增大100 m,切线调整时间下降1.5 s.半径1 000 m与直线的切线调整时间的差值约1.2 s,差异明显.回归直线的斜率表示流出角每增大1°,方向盘调整时间的变化值.曲线与直线的斜率基本相同,在0.17~0.18范围内.
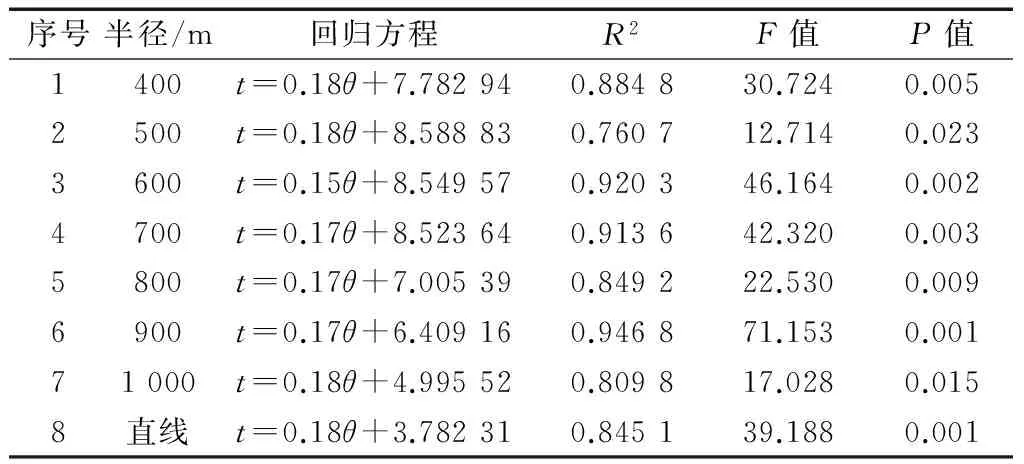
表1 方向调整时间与流出角线性回归结果Tab.1 Regression result between adjusting timeand departure time
由图3,圆曲线的方向调整时间均高于直线,不同主线线形条件下,回归直线基本平行.
综上,右转圆曲线影响切线调整时间,对方向调整时间随流出角的变化梯度不存在影响.
2.2 最小转向半径
采用不同设置水平下最小转向半径的95%置信区间下限建立图4所示高程图,其中,145.1 m、272.1 m分别为车辆重心高度1.6 m、3.0 m、驶入速度120 km·h-1时侧翻临界圆曲线半径.265.7 m、328.1 m、397.0、472.4 m分别为车辆驶入速度为90 km·h-1、100 km·h-1、110 km·h-1、120 km·h-1时的侧滑临界圆曲线半径.

图4 不同半径与流出角下最小转向半径Fig.4 The minimum turning radius for differenthorizontal radius and departure angle
最小转向半径呈扇形分布,车辆不发生侧翻行驶风险的比例低于30%,不发生侧滑行驶风险的比例仅占7%,集中于流出角5°以内、驶入速度100 km·h-1以内、主线平曲线半径600 m以上的区域.主线平曲线半径600 m以下,无论流出角大小,车辆均面临侧滑行驶风险.主线平曲线半径600 m以上,即使设置必要的超高,车辆仍然面临侧滑行驶风险.
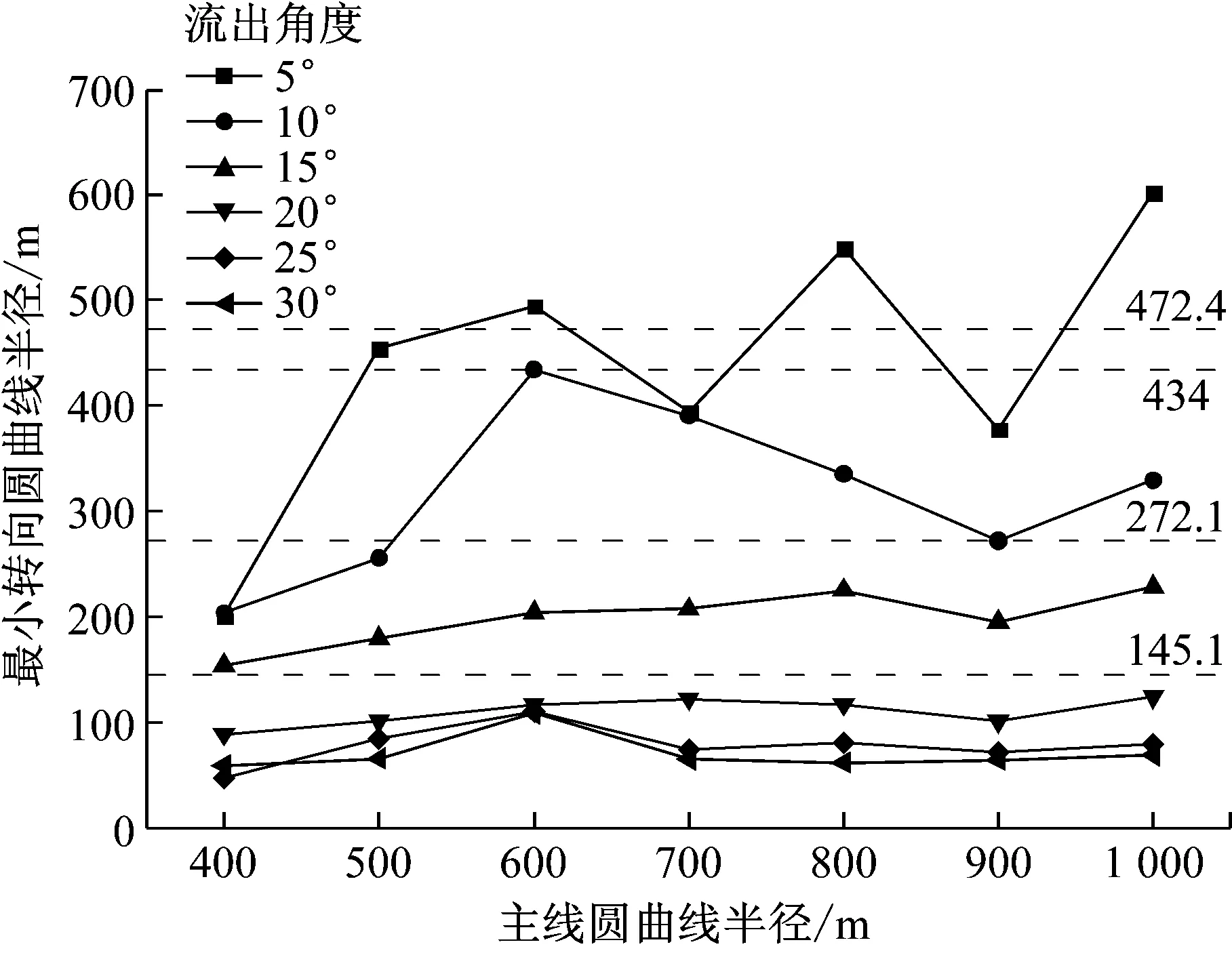
图5 最小转向半径随主线平曲线半径变化的折线图Fig.5 Line chart of the minimum turning radiusfor different horizontal curve
由图5,主线平曲线半径相同,车辆驶入紧急避险车道的最小转向半径随流出角增大而减小,且呈先急后缓的趋势.流出角相同,最小转向半径随主线半径的增大而增大,10°以内时变化幅度大,10°以上时基本稳定.
综上,避免车辆侧翻行驶风险时,半径宜大于600 m,流出角宜在10°内.
2.3 方向盘转角幅值
根据重复试验的方向盘转角幅值的平均值建立图6所示的高程图.幅值20°以内的比例低于20%.流出角低于20°时,不同半径、流出角对应的幅值基本相同,仅半径1 000 m的幅值略低.流出角在10°范围内时,方向盘转角幅值基本保持不变.流出角高于20°时,半径600 m对应的幅值明显低于其他半径的对应值,可能由实验误差引起.
由图7所示回归关系图可知,半径相同,方向盘转角幅值随流出角的增大而增大.除半径600m外,方向盘转角幅值的离散度随流出角增大并未出现明显的差异.流出角相同,方向盘转角幅值随半径的增大而增大.从车辆驶入紧急避险车道的难易程度来看,半径越大,流出角越小,驾驶员驶入紧急避险车道越容易.
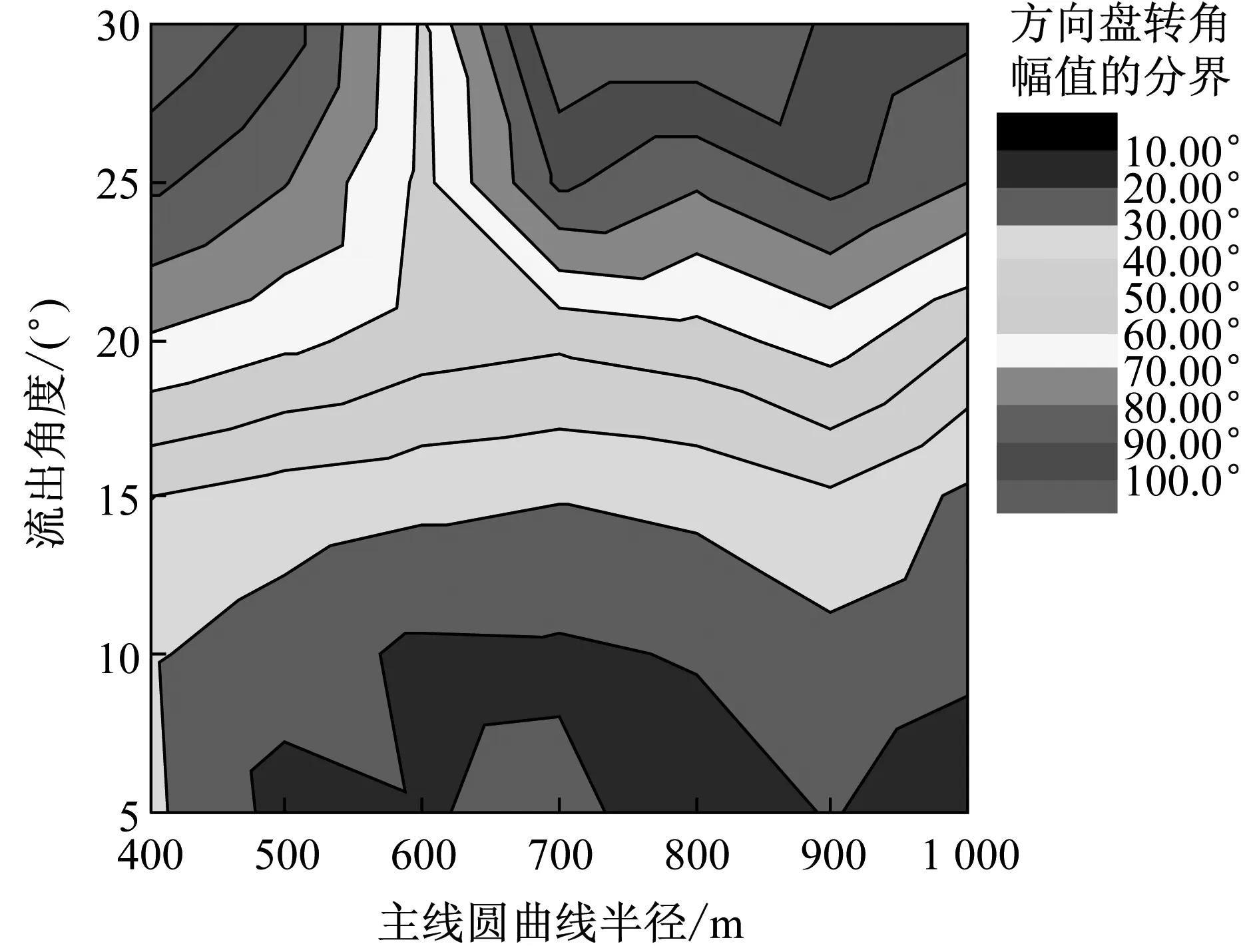
图6 不同半径与流出角下方向盘转角幅值Fig.6 Amplitude of steering wheel angle for differentradius and departure angle

图7 方向盘转角幅值与流出角的回归关系图Fig.7 Regression between amplitude of steering wheelangle and departure angle
方向盘转角幅值与流出角的函数回归关系如表2,方差分析的P值均小于0.05的显著性水平,说明不同流出角条件下,方向盘转角幅值存在显著差异.从拟合优度上看,半径600 m时,曲线的拟合优度较低.根据拟合公式,半径400~1 000 m分别对应1.2°、0°、0°、5.2°、1.8°、0°、0°的流出角时驾驶员的操作行负荷最低.根据计算结果,流出角在10°以内时,方向盘转角幅值基本相同,驾驶员驶入紧急避险车道的难易程度不存在明显差异.

表2 方向盘转角幅值与流出角度回归结果Tab.2 Regression results between steering wheel angle amplitude and departure angle
2.4 方向盘转角频率
根据重复试验的方向盘转角频率的均值做如图8所示高程图.方向盘转角频率在3°·s-1内的比例约为30%.半径600~700 m,流出角5°~10°时方向盘转角频率最低.半径900~1 000 m,流出角25°~30°时方向盘转角频率最高.流出角相同,方向盘转角频率随半径的增大呈先减小后增大的变化趋势,转折点半径600 m.半径相同,方向盘转角频率随流出角增大而增大.

图8 不同半径与流出角下方向盘转角频率Fig.8 Steering wheel angle frequency for differenthorizontal radius and departure angle
图9为流出角与方向盘转角频率的回归曲线图,流出角15°以内时,方向盘转角频率的离散度较小且基本相同,流出角高于15°时,方向盘转角频率的离散度明显增大,且随流出角度的增大而增大.流出角10°以内时,方向盘转角频率无明显增大,流出角度10°~15°时,方向盘转角频率小幅增大,流出角15°~20°时,方向盘转角频率陡增.流出角15°以内时,方向盘转角频率随半径的增大呈先减小后增大的变化规律,转折半径为700 m.

图9 方向盘转角频率与流出角度的回归关系Fig.9 Regression between Steering wheel anglefrequency and departure angle
表3为不同半径条件下方向盘转角频率与流出角度通过S型曲线进行拟合的统计表.方差检验结果的P值均小于0.05的显著性水平,说明流出角对方向盘转角频率存在显著影响.回归曲线对二者的拟合度非常好.通过卡方拟合优度检验,流出角与方向盘转角频率之间存在S型曲线关系.通过图9可知,流出角10°以内时,方向盘转角频率的拟合值接近于S型曲线的下限,而流出角达到15°时,方向盘转角变化频率开始显著增大.

表3 方向盘转角频率与流出角度回归关系结果Tab.3 Regression result between Steering wheel angle frequency and departure angle
3 基于二阶聚类的流出角度与引道长度设置阈值
通过二阶聚类,对不同半径与流出角度下的设置水平通过上述4项指标进行分类,结果如表4所示.分组2对应的方向调整时间小,最小转向圆曲线半径大,方向盘转角幅值与频率小,说明驾驶员在分组2的路段上驶入紧急避险车道的过程中,需要较短的引道长度,车辆面临的侧翻与侧滑风险小,驾驶员的操作负荷较低,心理紧张程度小.因此,分组2对应的水平更适合设置紧急避险车道.

表4 右转圆曲线二阶聚类结果统计表Tab.4 The second clustering results forright turn horizontal curves
通过单因素方差分析检验两组的统计量的差异显著性,如表5,检验结果的P值均小于0.001的显著性水平,表明聚类分析的两组结果的各指标存在明显的差异,聚类结果显著.
表6为聚类结果,半径600~700 m时,流出角宜设置在20°及其以内,半径为400~600 m、700~1 000 m时,流出角宜设置在15°及其以内.半径高于800 m时,半径对紧急避险车道的影响基本一致.

表5 分类结果方差检验表Tab.5 ANOVA test results

表6 右转圆曲线Ⅱ类水平结果Tab.6 The Ⅱ level result of right turn horizontal curve
在该分类的基础上,考虑车辆驶入紧急避险车道的横向行驶稳定性与引道的设置长度,对上述结果进一步分类见表7.其中,Ⅰ类风险为车辆在该水平下面临侧滑行驶风险,但若设置超高,即可避免该类行驶风险;Ⅱ类风险为车辆在该水平下驶入速度较高时会面临侧滑行驶风险;Ⅲ类风险为车辆重心较高时在该水平下会面临侧翻行驶风险;IV类为车辆面临侧翻行驶风险;N表示未出现上述风险.

表7 流出角与引道设置标准Tab.7 Specification for departure angle and approach length
综合考虑车辆的行驶风险与引道设置长度,主线为右转圆曲线时,紧急避险车道宜设置于圆曲线半径不小于1 000 m、流出角度不大于5°的条件.在条件困难时,可设置于主线圆曲线半径不小于600 m的圆曲线处,流出角度宜在10°范围内,且需设置较长的引道.
4 结语
本文采用驾驶模拟试验的方法,对设置于右转曲线的避险车道流出角度与引道长度进行研究,结果表明,右转圆曲线半径达到1 000 m时,失控车辆驶入紧急避险车道的驾驶行为与直线仍然存在差异,因此,对于紧急避险车道的设置,半径1 000 m不能作为将平曲线看作直线处理的分界点,后续试验需要扩大研究范围.建议将紧急避险车道设置于半径高于1 000 m的位置.条件困难时,可考虑设置于半径不低于600 m处.
引道与流出角度的设置受半径的影响.半径1 000 m及以上时,流出角度5°以内,引道为6 s设计行程.半径600 m~1 000 m,流出角5°以内,引道为9 s设计行程,流出角5°~10°,引道为12 s设计行程.
设置结论根据驾驶模拟试验结果得出,后期需通过实际运营数据对实验结果进行验证.
参考文献:
[1] TARSGIN A. The effect of length of grade on speed of motor vehicles[C]//Highway Research Board Proceedings, Oklahoma:[s.n.]: 1946:342-353.
[2] ABDELWAHAB W, MORRAL F J. Determining need for and location of truck escape ramps[J]. Journal of Transportation Engineering,1997, 123(5): 350.
[3] 张勇.山区高速公路长大下坡避险车道设置研究[D]. 北京:北京工业大学, 2008.
ZHANG Yong. Research on the truck escape ramp in the longitudinal steep slope of mountainous highway [D]. Beijing: Beijing University of Technology, 2008.
[4] 邓亚娟, 梁康, 张旭,等. 基于ADAMS/Car 的紧急避险车道入口安全研究[J]. 公路, 2016, 61(9): 201.
DENG Yajuan, LIANG Kang, ZHANG Xu,etal. Study of safety at entrance based on ADAMS/Car for the emergency escape ramp[J]. Highway, 2016, 61(9): 201.
[5] 牛建峰,王俊华,董宪元. 山区公路紧急避险车道驶入角研究[J]. 重庆交通大学学报(自然科学版), 2010, 29(4): 604.
NIU Jianfeng, WANG Junhua, DONG Xianyuan. Rasearch on the angle to truck escape ramps of mountain roads [J]. Journal of Chongqing Jiaotong University (Natural Science), 2010, 29(4): 604.
[6] AASHTO. A policy on geometric design of highways and streets (Green Book) [S]. [S.l.]:American Association of State Highway Transportation, 2001.
[7] 张翱东. 避险车道常见事故与设计缺陷的原因分析[J]. 甘肃科技纵横,2013,42(2):74.
ZHANG Aodong. Cause analysis of the common accidents occurred in the truck escape ramp and design defects [J]. Scientific & Technical Information of Gansu, 2013, 42(2): 74.
[8] 孙传夏. 避险车道设置的研究[J]. 公路交通科技(应用技术版), 2008,4(12): 179.
SUN Chuanxia. Research on emergency lane layout [J]. Journal of Highway and Transportation Research and Development (Technology), 2008, 4(12):179.
[9] 杨永占,马亮,荆坤. 山区高速公路长下坡避险车道线形参数设计[J]. 公路交通科技(应用技术版), 2015, 11(7):120.
YANG Yongzhan, MA Liang, JING Kun. Alignment design of the truck escape ramp in the longitudinal steep slope of mountainous highway [J]. Journal of Highway and Transportation Research and Development (Technology), 2015, 11(7): 120.
[10] 中交第一公路勘察设计研究院有限公司. 公路路线设计细则[S]. 北京:中交第一公路勘察设计研究院有限公司,2008.
China Communications Construction First Highway Consultants Co. Ltd. Design detailed regulations for highway alignment[S]. Beijing: China Communications Construction First Highway Consultants Co.Ltd., 2008.
[11] 中华人民共和国交通运输部.公路工程技术标准: JTG B01—2014[S]. 北京: 人民交通出版社股份有限公司, 2014.
Ministry of Transport of the People’s Republic of China. Technical standard of highway engineering: JTG B01—2014[S]. Beijing: China Communications Press Co. Ltd., 2014.
[12] 华杰工程咨询有限公司.公路项目安全性评价规范:JTG B05—2015[S]. 北京: 人民交通出版社, 2015.
Chelbi Engineering Consultants, Inc. Specifications for highway safety audit:JTG B05—2015[S]. Beijing: China Communications Press Co. Ltd., 2015.
[13] 宋灿灿,郭忠印,蔺琳. 紧急避险车道驶出角度及引道长度设置[J]. 同济大学学报(自然科学版),2016,44(4):587.
SONG Cancan, GUO Zhongyin, LIN Lin. Departure angle and approach length of truck escape ramp[J]. Journal of Tongji University (Natural Science), 2016,44(4):587.
[14] 张高强, 孙传夏, 程晓辉, 等. 基于颗粒流模拟的避险车道制动床长度确定方法[J]. 公路交通科技, 2011, 28(10): 118.
ZHANG Gaoqiang, SUN Chuanxia, CHENG Xiaohui,etal. Determining method of length of arrested bed of truck escape ramp based on particle flow simulation [J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 118.
[15] 陈渤. 山区高速公路长大下坡路段避险车道设计方法研究[D].成都: 西南交通大学,2007.
CHEN Bo. Research on truck escape ramp design in longitudinal steep slope of mountainous highway [D]. Chengdu: Southwest Jiaotong University, 2007.
[16] 中华人民共和国交通部公路司. 新理念公路设计指南[S]. 北京: 人民交通出版社, 2005.
Ministry of Communications of People’s Republic of China Highway design guidelines under flexibility[S]. Beijing: China Communications Press, 2005.

