直角梯形ETFE气枕塑性成形试验与数值分析
胡洪铭, 吴明儿, 刘以婷
(同济大学 土木工程学院,上海 200092)
乙烯-四氟乙烯共聚物(ETFE)薄膜材料具有透光性高、抗老化性好、自洁能力优秀、重量轻等特点,广泛运用于建筑领域.ETFE薄膜结构常以气枕形式作为建筑屋面或立面,应用于体育馆、展览馆、温室等.
ETFE薄膜材料力学性能的研究主要包含单轴拉伸和双轴拉伸试验.吴明儿通过对不同厚度的ETFE薄膜单轴拉伸试验得到了应力-应变曲线、抗拉强度及断裂延伸率,测定了ETFE薄膜的泊松比[1];Charbonneau通过单轴拉伸试验研究了徐变特性[2];吴明儿对ETFE薄膜进行了不同应力比的双轴拉伸试验,计算了ETFE薄膜的折算应力[3];崔家春用圆形气泡试验研究ETFE薄膜双向受力性能[4];Galliot完成了单轴拉伸试验、双轴十字形试验、气泡试验,对不同受力状态下材料性能实验数据进行了对比分析[5].
ETFE薄膜结构的研究一直是学者关注的重点.吴明儿对2个不同矢跨比的ETFE气枕模型进行了形状测试、加压以及铺砂加压试验,并用非线性有限元进行了数值分析[6].陈务军完成了ETFE气枕和气囊膜在不同荷载作用下的试验,并与数值结果进行了对比[7-8].许晶对ETFE气枕结构进行分析,得到了初始形态下膜面应力随气枕跨度、高度变化的规律以及受荷状态下气枕的位移、最大应力随初始内压变化的规律[9].顾磊对ETFE气枕模型进行了气枕形状测试、充气加压测试和气压一定的加载测试,把试验测试值与有限元分析结果进行比较,验证了数值方法的正确性[10].李鹏通过应力分析确定了 ETFE 气枕的破坏模式及失效准则,研究了尺寸、矢跨比及膜厚对气枕承载力的影响[11].吴明儿采用弹簧支撑代替 ETFE气枕中的压力系统,开发了弹簧支撑 ETFE枕式结构,并分析了其成形过程及受力特性[12].
目前ETFE气枕结构设计一般沿袭传统膜结构设计方法,包括找形分析,荷载分析及裁剪分析.裁剪分析将空间曲面近似展开为平面形状,裁剪完成的膜片通过焊接形成气枕.另一方面,利用ETFE薄膜材料优良的塑性变形能力,通过施加较高的内压使安装完成的平面ETFE薄膜产生较大的变形,然后将内压降到正常内压,利用ETFE薄膜材料自身产生的不可回复变形形成气枕结构曲面,这种方法称为平面裁剪的塑性成形法.Kawabata提出了利用加热以及加压使气枕成形的方法,并进行了试验以及理论分析[13].ZHAO基于平面裁切成形的方法,研究了ETFE气枕不同内压下结构的应力与应变特点[14].塑性成形方法得到的气枕形状与充气内压、充气时间、气枕边界形状、环境温度等都有关系,经历了塑性变形后的ETFE薄膜其材料特性也会出现变化.塑性成形可以大大简化裁剪和焊接工艺,提高材料的利用率,但塑性成形过程以及成形以后气枕的受力特性等的研究还很少.
本文针对平面裁剪塑性成形方法,设计制作了两个直角梯形ETFE气枕模型,进行了充气成形试验和循环充气加载试验.试验测量膜面高度和气压值并将测量结果与考虑ETFE薄膜弹塑性特性的有限元结果进行对比.
1 试验模型
试验模型为短边2.618 m、长边4.437 m、直角边3.15 m、斜边3.637 m的直角梯形,包含60°锐角和120°钝角,气枕根据设计尺寸进行平面裁剪.考虑ETFE薄膜的幅宽和气枕平面尺寸,上下膜面均由两片膜片经过高温热合焊接而成.上下层膜面的四边经高温热合焊接形成气枕结构,利用铝合金夹具固定在钢框架上,如图1所示.在气枕模型下膜面角部附近设置了两个孔,用来连接自动控制系统:一个用于充气和放气,另一个用于气压的测量与控制.ETFE薄膜采用日本旭硝子生产的材料,厚度为250 μm.


图1 ETFE气枕及其尺寸(单位:mm)Fig.1 ETFE cushion and its dimension (Unit: mm)
2 试验方法
2.1 试验准备
为了实现ETFE气枕充气和泄气、稳压的自动化,设计了一套简单实用的压力控制系统.该系统由空压机、三通管、压力开关、电磁阀、泄气阀、气压计以及无纸记录仪组成.压力开关可以在设定的气压下自动对电磁阀进行开闭,实现气枕的充气和泄气,从而控制气压.
试验在ETFE气枕下膜面设置了5个高精度激光位移计测量位移,测点布置如图2所示.
2.2 加载过程
将ETFE气枕试验分为两组,分别用气枕1和气枕2表示.从工程的角度,气枕1模拟了施工现在制作到使用的过程,气枕2模拟了工厂制作再到现场使用的过程.气枕1加载过程如下:首先,利用自动压力控制系统将气枕充气到内压2 kPa后立即泄气使内压降至0.5 kPa,接着使0.5 kPa内压维持70 min,此过程为充气成形阶段.充气成形阶段结束时可视为是气枕1的工作初始形态;最后,将内压升到3 kPa后立即降至0.5 kPa,共重复5次,此过程为循环充气加载阶段.内压加载过程如图3所示.

图2 激光位移布置图(单位:mm)Fig.2 Layout of laser displacement sensor (Unit: mm)
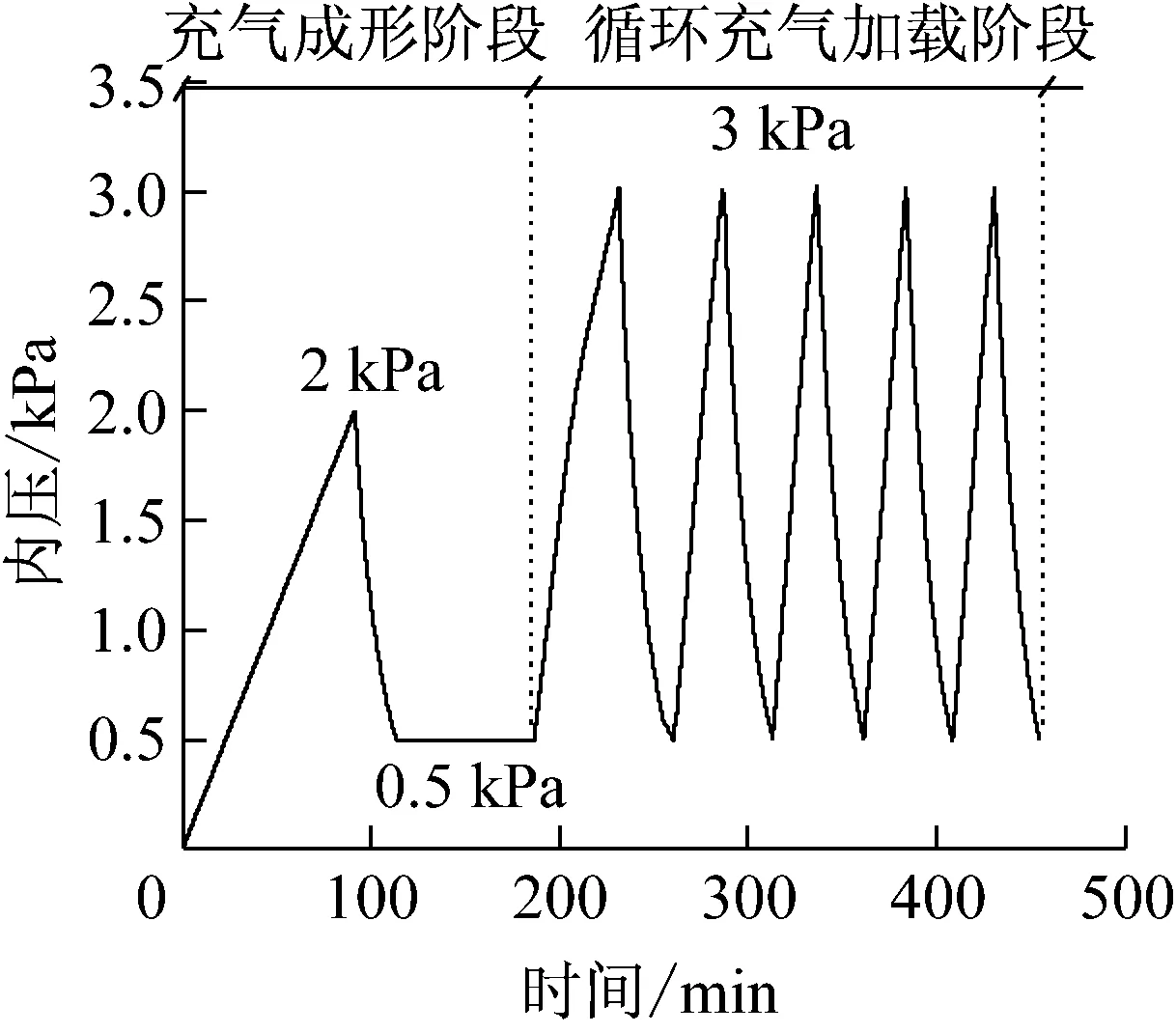
图3 气枕1内压加载过程Fig.3 Inflating and deflating process of Cushion 1
对于气枕2,内压控制过程如下:首先,将气枕内压升至2 kPa后立即将气枕内压降至0 kPa,维持该状态24 h,再将内压升到0.3 kPa而后立即降至0 kPa,共重复3次,再将内压充气到0.5 kPa立即降至0 kPa,共重复3次,此过程为充气成形阶段.接着将内压升至3 kPa后立即降至0.3 kPa,共重复3次,此过程为循环充气加载阶段.内压加载过程如图4所示.气枕2在成形阶段设置了2次0.3 kPa和0.5 kPa的循环加载,是为了测试成形得到的气枕在正常工作内压下形状的稳定性.

图4 气枕2内压加载过程Fig.4 Inflating and deflating process of Cushion 2
充气成形阶段目的在于使气枕从平面形状变为空间形状;循环充气阶段目的在于研究由塑性成形得到的气枕在风荷载等外载作用下的结构特性.
3 数值分析
采用ANSYS软件对ETFE气枕的充气以及泄气过程进行数值分析.为了简化,本文中ETFE薄膜材料采用多折线各向同性强化的弹塑性材料模型进行模拟,不考虑其粘性特性.对与试验中相同批次的ETFE薄膜材料进行了单轴拉伸试验,从应力应变曲线提取4个特征点,构成ETFE薄膜的折线材料模型,如图5所示.这4个点对应的应变与应力值分别为:点1(2.1%,14.0 MPa)、点2(12.2%,22.9 MPa)、点3(50.0%,37.1 MPa)和点4(100.0%,68.9 MPa).在点1之前ETFE薄膜处于弹性阶段,弹性模量为650 MPa,泊松比为0.42,应力超过点1以后进入弹塑性阶段.各点的应力应变值均采用真实应力与真实应变.
采用不考虑受压及受弯刚度的shell181单元划分气枕膜面,数值分析中忽略薄膜自重,考虑对称性仅计算一层膜面.
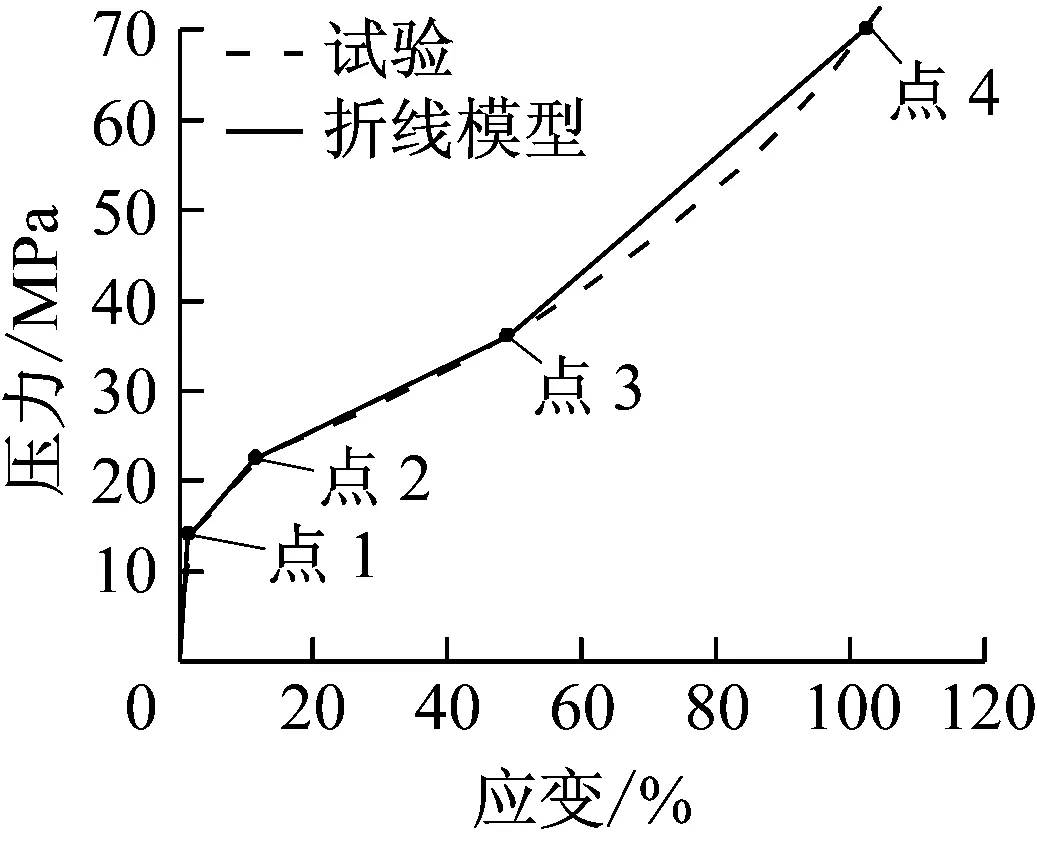
图5 ETFE薄膜各向同性强化弹塑性折线模型Fig.5 Multi-linear elastic-plastic model withisotropic hardening
4 试验与数值分析结果
各测点竖向位移与气枕内压的试验结果和数值分析结果,气枕1见图6所示,气枕2见图7所示.以下矢跨比计算中,将气枕跨度定义为梯形高度,即3 150 mm.
4.1 气枕成形阶段
气枕1经过2 kPa充气,泄气至0.5 kPa并保持70 min完成成形,在假定的0.5 kPa工作压力下气枕高度(即测点1位移)为335.1 mm,气枕矢跨比为1/9.4.在0.5 kPa内压保持70 min的时间内,气枕高度降低了2.2 mm,气枕形状变化不大.
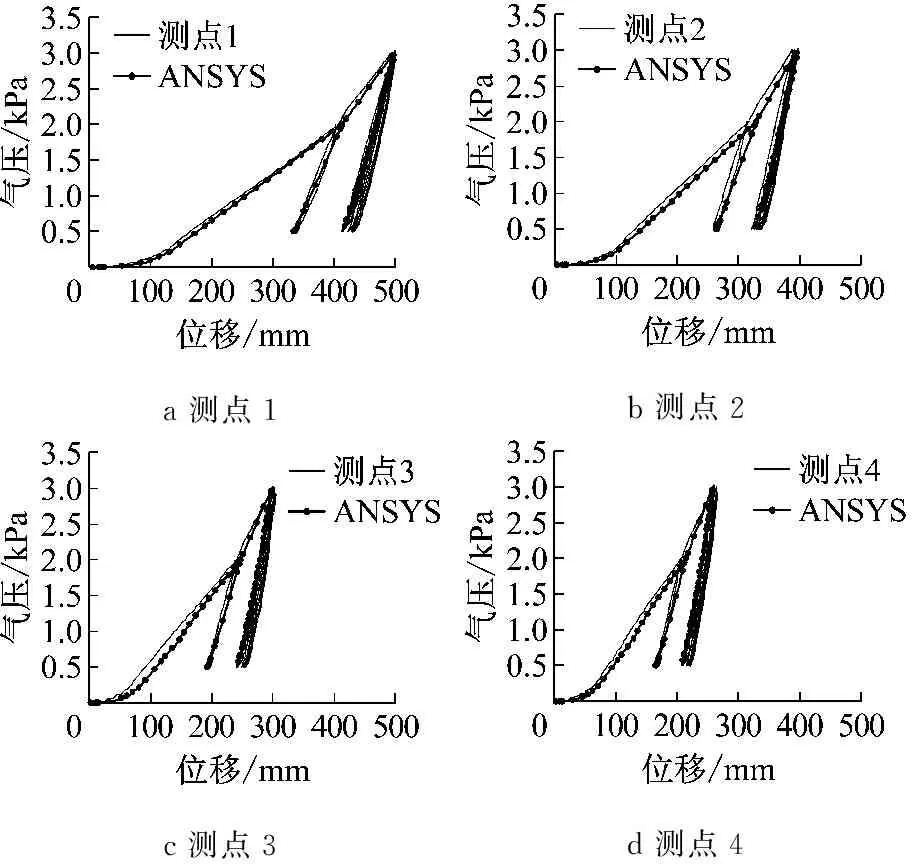
a测点1b测点2c测点3d测点4
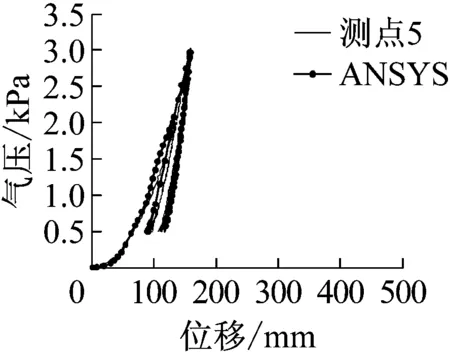
e 测点5图6 气枕1试验结果与数值结果Fig.6 Experimental and numerical results of Cushion 1

a测点1b测点2c测点3d测点4

e 测点5图7 气枕2试验结果与数值结果Fig.7 Experimental and numerical results of Cushion 2
气枕2经过2 kPa充气,泄气后静止24 h,0.3 kPa及0.5 kPa循环后,在假定的0.5 kPa工作压力下气枕高度为306.0 mm,气枕矢跨比为1/10.3.
比较充气至2 kPa后泄气至0.5 kPa时的气枕高度(357.1mm,矢跨比1/8.8),泄气后静止24 h使气枕形状产生较大的回缩.具体考察气枕2的回缩量.在泄气后内压0 kPa放置24 h过程中,气枕高度由318.3 mm降低到238.3 mm,表明气枕形状有较大的回缩(回缩量80 mm);通过0.3 kPa及0.5 kPa的循环加载,0 kPa时气枕高度为277.5 mm,表明有约50%的回缩量得到恢复.
进一步考察气枕膜面的应力,在2 kPa时膜面中央大部分区域进入塑性,最大Mises应力处于图5中点1和点2之间,气枕成形过程使膜面产生塑性变形.
数值分析较好地模拟了气枕1的成形过程.对于气枕2,数值分析无法模拟静止阶段的回缩现象.
4.2 循环加载阶段
对于循环加载,气枕1和气枕2表现出了相同的特性.
气枕从循环加载最初的0.5 kPa加载到2 kPa时,其形状与成形阶段加载到2 kPa时的形状基本重合.气枕1的气压位移几乎是直线,表明ETFE薄膜材料经过成形过程已经得到强化,ETFE气枕呈现弹性特性.气枕2在成形阶段产生的回缩基本得以消除.继续加载至3 kPa时,ETFE薄膜材料重新进入塑性,卸载至0.5 kPa时气枕产生残余变形.在3 kPa循环加载过程中,气枕表现较好的弹性特性,加载与卸载曲线几乎重合,继续产生的残余变形量很小.
循环加载结束时,气枕在0.5 kPa内压下的高度,气枕1为432.2 mm,气枕2为429.0 mm,两者矢跨比基本一致,约为1/7.3.
数值计算结果与试验结果基本一致,表明采用本论文的ETFE薄膜弹塑性模型可以进行循环加载的模拟.
5 结论
本文对两个直角梯形ETFE气枕进行了充气成形试验和循环充气加压试验,同时与考虑ETFE弹塑性特性的有限元结果进行了对比,得出以下结论:
(1) 通过最大压力为2 kPa的成形试验,两个试验模型得到的气枕的矢跨比分别为1/9.4和1/10.3;
(2) 气枕成形后经较长时间放置后,气枕形状有较大的回缩.气枕2在24h后的回缩使气枕的矢跨比从1/8.8变为1/10.3;
(3) 2 kPa的成形加载,使ETFE薄膜发生塑性变形,材料得到强化.由此方法成形得到的气枕,继续承载的压力不超过成形气压(2 kPa)时,气枕的变形近似为弹性变形;
(4) 超过成形气压的加载,使气枕产生新的塑性变形,但循环加载过程中气枕仍表现出较好的弹性特性;
(5) 考虑ETFE薄膜材料弹塑性特性的有限元分析,可以较好地模拟成形及循环加载过程,但是无法模拟气枕成形阶段的形状回缩.
参考文献:
[1] 吴明儿, 刘建明, 慕仝, 等. ETFE薄膜单向拉伸性能[J]. 建筑材料学报, 2008, 11(2): 241.
WU Minger, LIU Jianming, MU Tong,etal. Uniaxial tensile properties of ETFE foils [J]. Journal of Building Materials, 2008, 11(2): 241.
[2] CHARBONNEAU L, POLAK M A, PENLIDIS A. Mechanical properties of ETFE foils: testing and modelling [J]. Construction and Building Materials, 2014, 60: 63.
[3] 吴明儿, 赏莹莹, 李殷堂. 双轴拉伸下ETFE薄膜材料力学性能[J]. 建筑材料学报, 2014, 17(4):623.
WU Minger, SHANG Yingying, LI Yintang. Biaxial tensile mechanical properties of ETFE foil [J]. Journal of Building Materials, 2014, 17(4): 623.
[4] 崔家春, 吴明儿, 杨联萍. ETFE薄膜双向力学性能试验研究[J]. 建筑材料学报, 2016, 19(5):866.
CUI Jiachun, WU Minger, YANG Lianping. Experimental study on biaxial mechanical properties of ETFE film [J]. Journal of Building Materials, 2016, 19(5): 866.
[5] GALLIOT C, LUCHSINGER R H. Uniaxial and biaxial mechanical properties of ETFE foils [J]. Polymer Testing, 2011, 30(4): 356.
[6] 吴明儿, 刘建明, 张其林. ETFE 薄膜气枕模型试验研究[J]. 建筑结构学报, 2009, 29(6): 126.
WU Minger, LIU Jianming, ZHANG Qilin. Experimental study on ETFE foil cushion [J]. Journal of Building Structures, 2009, 29(6) : 126.
[7] 陈务军, 唐雅芳, 任小强, 等. ETFE 气囊膜结构设计分析方法与数值分析特征研究[J]. 空间结构, 2010, 16(4): 38.
CHEN Wujun, TANG Yafang, REN Xiaoqiang,etal. Analysis methods of structural design and characteristics of numerical algorithm for ETFE air inflated film structures [J]. Spatial Structures, 2010, 16(4): 38.
[8] 赵兵, 陈务军, 何艳丽,等. ETFE薄膜双层气枕结构试验研究[J]. 空间结构, 2013, 19(1): 65.
ZHAO Bing, CHEN Wujun, HE Yanli,etal. Experimental study on double-layer ETFE foil cushion [J]. Spatial Structures, 2013, 19(1): 65.
[9] 许晶. 气枕式ETFE膜结构的静力分析[D]. 北京:北京工业大学, 2005.
XU Jing. The static analyses for ETFE air cushion membrane structure [D]. Beijing: Beijing University of Technology, 2005.
[10] 顾磊, 王鹏, 陈世平, 等. ETFE气枕模型试验与有限元分析[J]. 建筑结构学报, 2012, 33(5): 46.
GU Lei, WANG Peng, CHEN Shiping,etal. Experimental study and FEA of ETFE cushion [J]. Journal of Building Structures, 2012, 33(5): 46.
[11] 李鹏, 杨庆山, 王晓峰. 基于共同作用模型的ETFE气枕力学性能研究[J]. 工程力学, 2014, 31(9): 203.
LI Peng, YANG Qingshan, WANG Xiaofeng. Study on mechanical properties of ETFE cushions based on interaction model [J]. Engineering Mechanics, 2014, 31(9): 203.
[12] 吴明儿, 毛元庆. 双弹簧支撑ETFE枕式膜结构性能研究[J]. 建筑结构学报, 2013, 34(11): 57.
WU Minger, MAO Yuanqing. Studies on structural behavior of ETFE foil spring cushion structure consisting of two spring units [J]. Journal of Building Structures, 2013, 34(11): 57.
[13] KAWABATA M, NISHIKAWA K, MORIYAMA F,etal. Study on heat and pressure shaping of ETFE film pneumatic panel, (part 1) behavior and material constant when heating ETFE film, (part 2) examination of behaviors on heat and pressure shaping[C]// Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan. [S.l]: Architectural Institute of Japan, 2005: 929-932.
[14] ZHAO B, CHEN W, HU J,etal. Mechanical properties of ETFE foils in form-developing of inflated cushion through flat-patterning [J]. Construction and Building Materials, 2016, 111: 580.

