水泥混凝土路面传力杆应力分析力学模型
姚 尧, 谈至明, 朱唐亮, 肖 建
(同济大学 道路与交通工程教育部重点实验室, 上海 201804)
在水泥混凝土路面接缝处设置传力杆,可有效地减小水泥混凝土路面接缝两侧挠度差,以及水泥混凝土路面板接缝边缘的荷载应力,提高路面的服务性能和使用寿命[1].对传力杆的受力状态以及传荷效应,目前的分析方法有基于弹性地基梁的近似解析法[2-4]和基于有限元的数值法[5-13]二种.弹性地基梁法是将传力杆视为一埋入均质弹性介质中的梁,即文克勒地基梁,这种将混凝土面层、基垫层和路基近似为均质弹性支撑的近似处理过于粗糙,无法通过室内模拟试验及现场测试结果反算得到稳定的传力杆的支撑模量;通过有限元方法,分析了传力杆和混凝土界面接触应力,认为混凝土的应力集中水平随着传力杆的直径和间距的增大显著降低,而长度对应力的影响不显著,三维有限元方法虽能够解析传力杆的受力状态和传荷效应,但其计算精度受单元特性、网格划分尺寸等影响,且规律难寻,无法给出具体计算式.因此,寻找简明实用、精度良好的力学模型,对于更好地把握路面传力杆系统的受力状况,改进其设计方法具有理论和实用意义.
1 传力杆受力状态的三维有限元解
1.1 三维有限元模型
不考虑路面板横向差异的二块路面板及传力杆系统的力学模型如图1所示,图中,I为主动梁,其挠曲由外荷载与传力杆共同作用引起的;II为被动梁,挠曲仅由传力杆作用引起的;L为路面板板长;h为路面板厚度;b为传力杆横向间距(即梁宽);δ为接缝缝隙宽度;d为传力杆直径;ls为传力杆填入混凝土长度;k为地基反应模量;路表面自由或路表面承载局部分布荷载;c为局部分布荷载宽度;q为分布荷载集度;梁两侧面为滑支边界,法向位移和剪应力为零,接缝缝隙的传力杆周边为自由边界.利用ANSYS有限元软件,构建了三维有限元模型,传力杆与混凝土均采用SOLID65号实体单元,传力杆与混凝土接触面采用TARGE170、CONTA173号接触单元模拟.单元网格在靠近接缝及钢筋四周密划,如图2所示.

图1 路面传力杆系统的力学模型Fig.1 Mechanical model of pavement dowel bar system

图2 单元网格划分Fig.2 Finite element meshing
1.2 传力杆与混凝土的接触状态
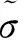

a 完全黏接

b 部分黏接

c 完全分离图3 不同接触模型下传力杆与混凝土界面应力状态Fig.3 Interfacial stress state between dowel barand concrete under different contact models

传力杆钢筋与水泥混凝土界面的黏结强度(化学胶着力)较小,远小于混凝土材料本身的抗拉、抗剪强度,因此,即便它们初始处于完全黏合状态,在重复荷载作用下也极易破坏脱开;当界面受拉脱开后,界面的剪应力快速上升,很快会超过其界面黏结强度而滑移,因此,在重复荷载作用下的传力杆钢筋与水泥混凝土之间工作状况应更趋近于界面仅传递受压应力状态,当传力杆涂沥青或加套保护筒,则初始即为完全分离状态.
1.3 梁挠曲效应和力学模型简化
尽管传力杆与混凝土界面接触状况对它们界面应力影响很大,但从混凝土梁挠曲变形来看,其影响很小可忽略,传力杆与混凝土界面三种接触状况下的被动梁的平均挠曲线几乎完全重合.
埋入混凝土的传力杆长度与直径比一般大于6,无论是从梁挠曲视角还是从传力杆与混凝土界面应力状态来看,传力杆均可视为与梁同长的.研究发现,当关注传力杆传荷机理和接缝端部的传力杆与混凝土界面应力时,路面板可视为半无限长.由此,结构的力学模型简化传力杆与路面板同长,且均趋于半无限长,钢筋传力杆与水泥混凝土界面完全分离状态,如图4所示,图中Qs和Ms分别为传力杆传递的剪力与弯矩,δ为接缝宽度.
图4 简化的力学模型Fig.4 Simplified mechanics model
2 双层弹性地基梁模型的拟合
2.1 双层弹性地基梁模型及解
将图4所示力学模型中传力杆移至混凝土梁上部,并按弯曲刚度相等原则将圆钢筋转化与混凝土等宽的薄钢梁,薄钢梁与混凝土梁之间有竖向弹簧相连,其反应模量记作kv,从而抽象得到弹性地基上的双层叠合梁模型[14].
当传力杆缝隙中点的剪力与弯矩分别为Qs和Ms时,薄钢梁与混凝土梁的挠度ws和wc解为
ws=e-αx(A1sinαx+A2cosαx)+
e-βx(A3sinβx+A4cosβx)
wc=r1e-αx(A1sinαx+A2cosαx)+
r2e-βx(A3sinβx+A4cosβx)
(1)
式中:Qs和Ms分别为传力杆传递的剪力与弯矩;Ds和Dc为上、下层梁的弯曲刚度,计算如下:
式中,Es和Ec分别为钢筋和混凝土的弹性模量.
2.2 混凝土梁的挠曲
文献[11]推荐的无夹层对上、下层梁间的竖向反应模量kv的计算式为
(2)
式中:vs和vc分别为钢筋与混凝土的泊松比;hs为上层梁的等效厚度,计算如下:
三维有限元模型和双层梁模型求得的传力杆端部作用剪力Qs时,双层梁模型的混凝土梁挠曲线(实线)和三维有限元解的混凝土梁平均挠曲线(虚线)如图5所示,图中纵坐标φ为任意位置挠度w与双层梁模型的混凝土梁端最大挠度wmax的比值,即φ=w/wmax,横坐标β为任意位置梁长x与混凝土梁刚度半径l的比值,即β=x/l,混凝土梁刚度半径l计算如下:

图5 梁体弯沉对比Fig.5 Comparison of beam deflection
从图5可以看到,两种模型求出的混凝土梁挠曲线几乎重合,这说明弹性地基上双层梁模型拟合混凝土梁的挠曲问题具有良好的精度.
2.3 层间竖向反应模量的修正
双层梁模型计算得到的上、下层梁之间的相对挠度(ws-wc)、相对转角(θs-θc)及上、下层梁界面压应力σc均为梁宽b上的平均值,而实际结构中此三者主要源于传力杆直径d范围内混凝土的局部量,其值上有差异.研究发现,层间竖向反应模量kv乘以一挠度修正系数ξw,即可消除双层梁模型的梁端部处上下层梁的相对挠度(ws-wc)与实际传力杆与混凝土梁间相对挠度的差异;层间竖向反应模量kv乘以一转角修正系数ξθ,即可使得双层梁模型的梁端部处上下层梁的相对转角(θs-θc)与实际传力杆与混凝土梁之间相对转角相同;当对层间竖向反应模量kv乘以一压应力修正系数ξσ,则可保证双层梁梁端部处层间反力合力与实际界面压应力合力Σσc相等.修正系数ξw、ξθ和ξσ与混凝土梁高h、梁宽b及传力杆直径d,以及传力杆与混凝土模量比Es/Ec有关.由于传力杆与混凝土模量比Es/Ec的影响较小且其值变化幅度较小,取常量7.0,忽略该因素变化,因此基于梁端面处相对挠度(ws-wc)、相对转角(θs-θc)及界面压应力合力Σσc等效的层间竖向反应模量修正系数ξi的回归式可表示如下:
ξi=(b-a1i)(Aid2+Bid+Ci)+
(3)
式中:b、d和h均取以m为单位对应的数值;i为w、θ或σ,对应的回归系数a1i、a2i、Ai、Bi、Ci和Di值见表1.

表1 回归式(3)的回归系数a1i、a2i、Ai、Bi、Ci和DiTab.1 Regression coefficients of Regression Equation (3): a1i, a2i, Ai, Bi, Ci and Di
3 传力杆的传荷系数
在仅关注混凝土梁挠曲时,传力杆传递的剪力Qs可假设为与两侧混凝土梁端弯沉差Δwc成正比,传递的弯矩Ms可假设与两侧混凝土梁端转角差Δθc成正比,即
Qs=kτΔwckl,Ms=kMΔθck
(4)
式中:kτ为剪力传递系数,即传荷效应的抗剪刚度;kM为弯矩传递系数,即传荷效应的抗弯刚度;Δwc和Δθc计算如下:
(5)
将传力杆传递的剪力与弯矩视为作用于I、II梁上大小相等方向相反的反对称荷载,则认为δwI≈δwII,δθI≈δθII.
3.1 抗剪刚度
当传力杆在缝隙中点处于纯剪状时,主动梁与被动梁在梁端面处传力杆与混凝土之间的相对挠度大小相等,其位移差由两部分组成:接缝两侧上下层梁的相对位移w01;传力杆在缝隙段的弯曲及剪切变形w02.计算式为
(6)
式中:Δs为传力杆与混凝土梁间的松动量;As为钢筋截面积;Gs为钢筋剪切模量,计算如下:
将w01视为混凝土与传力杆的相互作用变形,定义其模量为Sc;将后者视为传力杆的抗剪切变形,定义其模量为Sd为
当不考虑传力杆与混凝土间的松动,即Δs=0时,传力杆的抗剪刚度kτ计算如下:
(7)
式中,δ为接缝宽度.
3.2 抗弯刚度
当传力杆仅传递单位弯矩时,主动梁与被动梁在梁端面处传力杆与混凝土之间的相对转角大小相等,其转角差可分为两部分计算:上、下层梁之间的转角差θ01和钢筋受弯产生的转角差θ02.计算如下:
(8)
式中:Δθ为传力杆与混凝土梁间松动量导致的转角差;Ds为钢筋抗弯刚度.
将θ01视为钢筋与水泥混凝土梁相对作用变形,定义其模量为Cc;将θ02视为钢筋自身的抗弯转角变形,定义其模量为Cd,则有
当不考虑传力杆与混凝土间的松动,即Δθ=0时,传力杆的抗弯刚度kM计算如下:
(9)
当已知传力杆与混凝土间的松动宽度2Δ时,传力杆的抗剪刚度kτ和抗弯刚度kM仍可按式(7)和式(9)近似估计,只需将缝隙宽度δ替换为两侧传力杆与混凝土间松动宽度2Δ与缝隙宽度δ之和δ′=2Δ+δ即可.
取结构参数b=h=0.3 m,d=0.02 m,δ=0.01 m,Es=210 GPa,vs=0.30,Ec=30 GPa,vc=0.15,地基反应模量k=100 MN·m-3,当主动梁承受梁端集中荷载P=10 kN作用时,被动梁梁端位移与主动梁梁端挠度比值为0.931 6;若不考虑传力杆传递弯矩的能力,即kM=0,则被动梁与主动梁梁端挠度比值为0.931 3,在两种条件下传力杆传递的剪力与外荷载的比值均为0.482 2.当传力杆与混凝土间松动宽度Δ=0.04 m时,考虑传力杆传递弯矩与不传递弯矩时,被动梁与主动梁梁端挠度比值均为0.513 6,传力杆传递的剪力与外荷载的比值均为0.339 3.结果表明传力杆传递弯矩的能力对梁端挠度比及传力杆剪力传递量的影响很小,可忽略.
4 基层对接缝传荷效率的影响
当路面板下设置半刚性基层时,主动梁挠度减少,且由基层挠曲面的连带效应,被动梁有一定量的挠曲,因此相邻梁的挠度差减少明显,其传力杆的传荷量也相应减少.将设有半刚性基层的路面结构视为三段梁模型,如图6所示,左右两段(a、c段)视为弹性地基上的双层梁模型,裂缝处的基层(b段)视为弹性地基上的单梁.

图6 双层地基梁传荷Fig.6 Load transfer model of double - layerfoundation beam
取上层梁刚度D1=20 kPa·m4,地基反应模量k=100 MN·m-3,当梁端作用集中荷载P时,代入边界条件与连续条件可解得各段梁的挠度解,进而可求得传力杆传递的剪力Qs与弯矩Ms.以接缝处的荷载传递比λσ和挠度比λw作为表征接缝传荷效率的指标:荷载传递比λσ为传力杆传递的剪力Qs与作用荷载P的比值,挠度比λw为主动梁与被动梁梁端挠度比值.根据计算结果得到,在不同基层刚度D2时,挠度比λw、荷载传递比λσ与接缝抗剪刚度kτ间关系如图7和图8所示.

图7 λw-kτ关系曲线Fig.7 Relationship curves of λw-kτ

图8 λσ-kτ关系曲线Fig.8 Relationship curves of λσ-kτ
图7和图8表明,挠度比λw、荷载传递比λσ与接缝抗剪刚度kτ均呈S型关系曲线,随着基层刚度D2的逐渐增大,λw-kτ关系曲线逐渐向内移,而λσ-kτ关系曲线则逐渐外移.当kτ一定时,接缝的挠度比随基层刚度的增大而增大,而荷载传递比则随着基层刚度的增大而减小,且其减小幅度较挠度比的增大幅度更明显.本算例结果表明基层的存在可使接缝两侧挠度比增大,接缝传递的剪力减小.Ioannides等在文献[7]给出的λw-kτ关系图即为图7中D2/D1=0的曲线,它未考量基层刚度影响的结果,其适用范围很狭窄.
5 结论
(1) 利用三维有限元模型分析了水泥混凝土路面中传力杆与水泥混凝土的三种接触状况:完全黏合、受压黏合受拉脱开和完全分离条件的传力杆与混凝土的接触应力,指出了在正常工作时传力杆与水泥混凝土间大多呈完全分离状态.
(2) 水泥混凝土面层和传力杆系统可简化为双层梁结构,对于端部的传力杆与混凝土相对位移、相对转角及两者的挤压力,只需对双层梁层间竖向反应模量进行修正即可.对双层梁竖向反应模量的位移修正系数ξw、转角修正系数ξθ和挤压力修正系数ξσ的变化规律进行分析和归纳,给出它们的回归式.由于双层梁模型考虑了混凝土面层、基垫层和路基各自的材料参数与尺寸参数的影响,因此,当已知各层材料参数与尺寸参数时,可依据该模型快速精确计算出传力杆的受力状态.
(3) 关注混凝土梁挠曲变形时,传力杆系统的传荷作用可用接缝混凝土梁间的抗剪刚度kτ与抗弯刚度kM表征,给出了抗剪刚度kτ与抗弯刚度kM的计算式,并通过算例闸明了传力杆传递弯矩的作用很小,可忽略.确定传力杆的抗剪刚度kτ与抗弯刚度kM后,可建立相应的接缝传荷模型,进而计算得到荷载作用下单根传力杆传递的荷载量.
(4) 计算分析了梁端部作用集中荷载时,有基层的地基梁接缝传荷问题,给出了接缝挠度比λw、荷载传递比λσ与接缝抗剪刚度kτ的S型关系曲线,指出在接缝抗剪刚度相同条件下,基层存在可使接缝两侧挠度比增大,接缝传递的剪力减小.
参考文献:
[1] 锁利军, 王秉纲, 陈拴发,等. 接缝设传力杆水泥混凝土面层结构力学分析[J]. 长安大学学报(自然科学版), 2008, 28(3):30.
SUO Lijun, WANG Binggang, CHEN Shuanfa,etal. Numerical analysis of mechanics of concrete overlay in transverse joint with dowel bars[J]. Journal of Chang’an University (Natural and Science), 2008, 28(3):30.
[2] TIMOSHENKO S P. On the correction for shear of the differential equation for transverse vibrations of prismatic bars[J]. Domestic Animal Endocrinology, 1990, 7(2):239.
[3] BRADBURY R D. Load and deflection characteristics of dowels in transverse joints of concrete pavements [C]∥18th Highway Research Board. [S.l.]:National Research Council, 1938:156-157.
[4] BRADBURY R D. Reinforced concrete pavements[R].Washington D C: Wire Reinforcement Institute, 1938.
[5] HUANG Y H, DENG X J. Finite element analysis of jointed concrete pavements[J]. Journal of Transportation Engineering, 1983, 109(5):689.
[6] 姚祖康.水泥混凝土路面荷载应力的有限元分析[J]. 同济大学学报(自然科学版), 1979(6):48.
YAO Zukang. Finite element analysis of load stress on cement concrete pavement[J]. Journal of Tongji University (Natural and Science), 1979(6):48.
[7] IOANNIDES A M, Korovesis G T,etal. Analysis and design of doweled slab-on-grade pavement systems[J]. Journal of Transportation Engineering, 1992, 118(6):745.
[8] GUO H, SHERWOOD J A, SNYDER M B. Component dowel-bar model for load transfer systems in PCC pavements[J]. Journal of Transportation Engineering, 1995, 121(3):289.
[9] 蒋应军, 戴经梁. 传力杆与混凝土界面的接触应力[J]. 中国公路学报, 2007, 20(2):29.
JIANG Yingjun, DAI Jingliang. Contact stresses at interfaces between dowels and surrounding concrete[J]. China Journal of Highway & Transport, 2007, 20(2):29.
[10] 刘旭峰. 水泥混凝土路面接缝传荷衰变试验研究[D]. 西安: 长安大学, 2012.
LIU Xufeng. Study on the decay of load transfer on cement concrete pavement[D]. Xi’an: Chang’an University, 2012.
[11] 李洛克. 水泥混凝土路面传力杆的传荷失效机理研究[D]. 哈尔滨:哈尔滨工业大学, 2012.
LI Luoke. Research on the load transfer failure mechanism for dowel bar in concrete pavement[D]. Harbin: Harbin Institute of Technology, 2012.
[12] 罗勇,袁捷.三维有限元法对水泥混凝土道面接缝传荷作用的模拟方法研究[J]. 公路交通科技, 2013,30(3):32.
LUO Yong, YUAN Jie. Research on simulation method for load transfer of joints of cement concrete pavement by 3D finite element method[J]. Journal of Highway & Transportation Research & Development, 2013, 30(3):32.
[13] ZHOU Z. Stress concentration analysis in concrete round dowels for airport jointed rigid pavement system[C]//International Conference on Transportation Engineering. Chengdu: American Society of Civil Engineers, 2011: 1566-1571.
[14] 谈至明. 具有弹性夹层的文克勒地基上双层叠合梁的解[J]. 应用力学学报, 2000, 17(3):23.
TAN Zhiming. Solution to Bilayer beams with elastic interlayer on winkler foundation[J]. Chinese Journal of Applied Mechanics, 2000, 17(3):23.
[15] 张怀志. 普通水泥路面传力杆及拉杆研究[D]. 哈尔滨:哈尔滨工业大学, 2007.
ZHANG Huaizhi. Study on the dowel and tie bar in jointed plain concrete pavement[D]. Harbin: Harbin Institute of Technology, 2007.
[16] LI X, MA S, HOU X. The analysis of dowel and tie bars effects on curling up in concrete pavement slabs[C]//Ninth International Conference of Chinese Transportation Professionals. Harbin: American Society of Civil Engineers, 2009:1-6.

