考虑货车因素的高速公路短期交通流风险预测
张兰芳, 赵 焜
(同济大学 道路与交通工程教育部重点试验室, 上海 201804)
公安部交通管理局的统计数据显示,2016年全国发生货车责任道路交通事故5.04万起,造成2.5万人死亡、4.68万人受伤,分别占汽车责任事故总量的30.5%、48.23%和27.81%,远高于货车保有量占汽车总量的比例[1].货车交通事故多发,已成为严重的交通安全隐患.因此货车对道路安全的影响研究就显得尤为重要.鉴于货车事故的严重性,如果能够采用主动防控技术,在事故尚未发生、但有一定征兆时,采取措施来避免事故的发生,对于改善交通安全具有重要意义.
在货车对交通影响的研究中,Gazis等[2]首次提出了“移动瓶颈(moving bottleneck)”的概念,解释重型车辆对通行能力产生的影响.Middleton等[3]针对混行及小客车专用道的事故类型及比例进行调查分析,结果表明客车专用道的事故率明显低于混行车道事故率,且混行车道货车与客车发生碰撞的概率极高.Vadlamani等[4]发现主要类型的货车交通事故发生的概率与货车比例、交通量、以及天气交通状况等因素有关.Yang等[5]对小汽车和货车的混合交通流进行了研究,发现在不同的小汽车与货车组合中,小汽车跟随货车的组合对于交通流稳定性影响更大.在货车安全方面,货车事故严重程度的影响因素分析也是近年来的研究热点[6-8].
近年来交通智能化发展迅速,交通流实时数据的获取及存储更加高效.越来越多学者开始研究利用实时交通流数据进行风险评估.Oh等[9]研究发现5 min间隔的速度标准差是检测事故的最佳参数,并采用非参数贝叶斯(non-parametric Bayesian)分类模型分析事故风险.Abdel-Aty和Pande[10]首先将事故风险预测作为一种分类问题进行研究,利用基于贝叶斯判别法的概率神经网络法(Probabilistic Neutral Network),最终训练得到PNN 模型,可以识别70%的事故.Pande等[11-12]采用多层感知神经网络(Multi-layer Perceptron Neural Network)和正态径向基神经网络(Normalized Radial Basis Function),分别针对追尾事故、侧碰事故进行实时事故风险预测模型建模,达到了理想的分类精度.Yu等[13]利用支持向量机(Support Vector Machine)和贝叶斯逻辑回归(Bayesian Logistic Regression)对山区高速公路进行实时交通流风险预测,证明在数据集较小时,支持向量机具有更好的预测性.孙剑等[14]应用贝叶斯网络(BN)模型对快速路实时交通流参数与事故风险进行建模,事故预测准确率达到76.94%.
综上,在货车对于交通的影响的研究中,国内外学者从“移动瓶颈”理论出发,研究微观条件下,货车对交通流的扰动.在研究方法上,多利用仿真软件得到交通流模拟数据,而较少采用实时的交通流数据.在实时交通流风险评估的研究中,使用的模型从传统统计模型逐渐向人工智能模型方面发展.存在的问题是,由于国外货车比例较低,且货车性能与小汽车差别不明显,因此在研究中忽略了货车对交通流风险的影响.针对国内高速公路货车比例及货车事故比例较高的问题,对货车造成的交通流风险还需进行量化研究.通过在特征变量中加入货车因素,提高了高速公路短期交通流风险预测模型的预测精度,为国内货车交通安全研究在事故预测方面提供借鉴.
1 数据准备
1.1 交通流数据与事故数据
本文数据采集自沈海高速公路(G15)上海段,采集时间为2014年1月至2015年9月.交通流数据通过线圈检测器进行采集,可得到流量、速度、占有率等交通参数.G15上海段共布设检测器21套,平均间距为4.5km,检测器数据采集周期为20 s.交通流数据采集周期较短会产生数据噪声,因此本文按照5 min时间间隔对交通流数据进行集计[10].提取事故发生前20 min的数据,以5 min为单位时段,将数据分为事故发生前0~5 min,5~10 min,10~15 min和15~20 min 4个时间段.
共采集事故数1 220起,其中货车相关事故占总事故比例为61%,如图1a所示.统计得到事故发生时货车比例平均为34%,即本路段货车事故比例明显高于货车比例,表明货车对于本路段的通畅与安全造成了较大的影响.事故形态分布如图1b所示.考虑到追尾,碰擦等事故多由交通流拥挤或紊乱等造成,此类事适合使用交通流参数进行预测.并且从图1b中可以看出追尾和碰擦两类事故占总事故数的45%,比例较大,所以事故研究主要为追尾和碰擦事故.
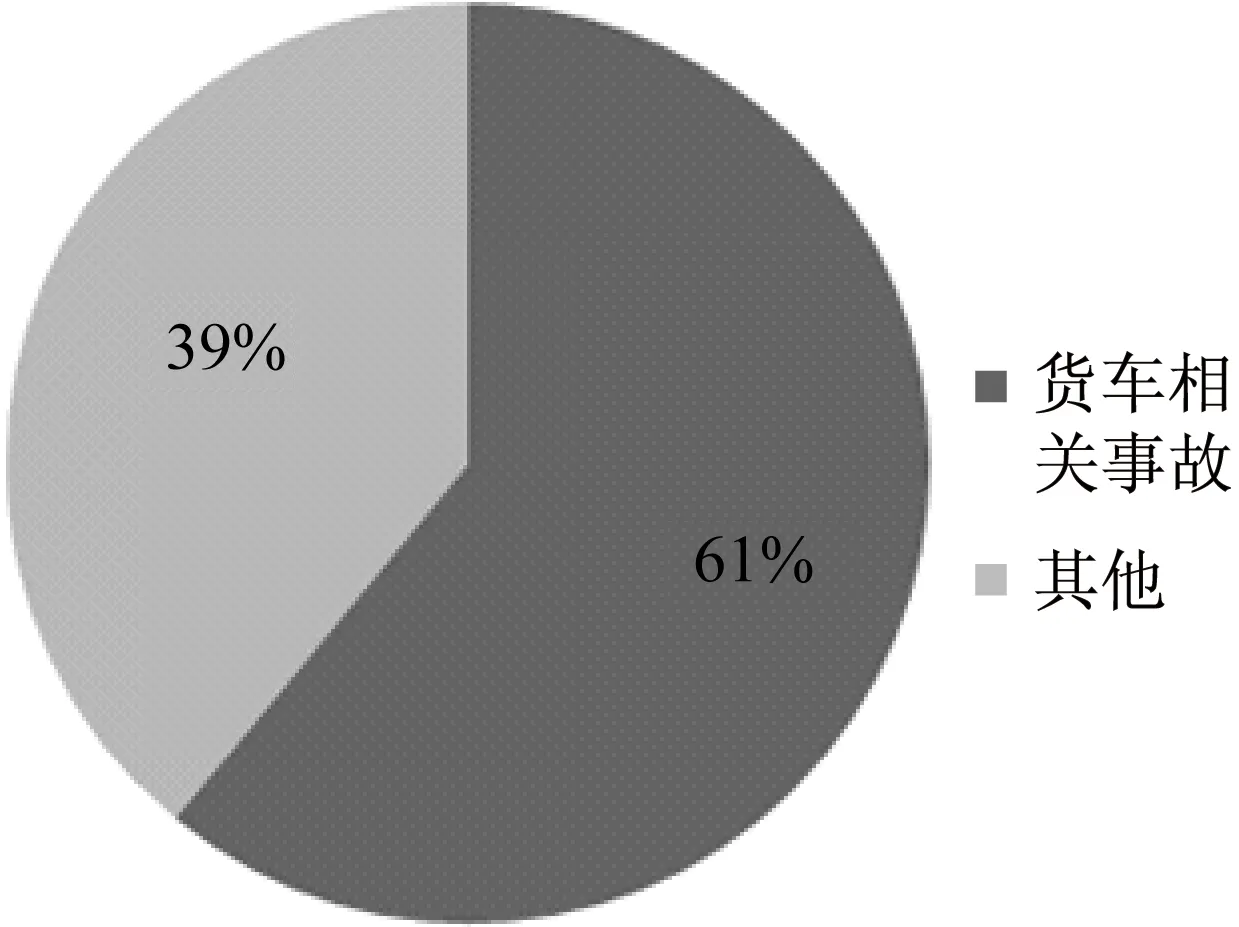
a
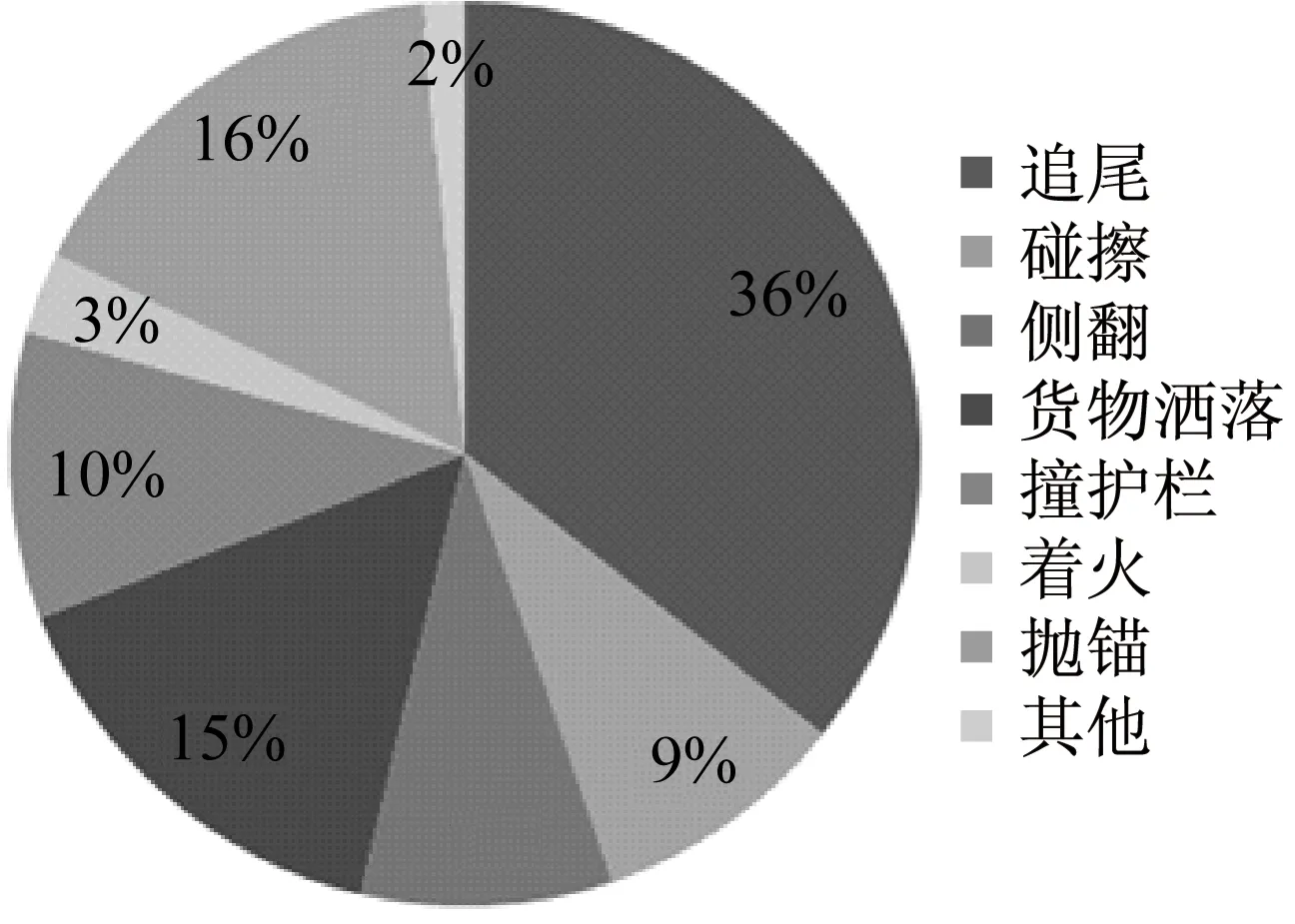
b图1 事故数据分类统计Fig.1 Classified statistics of crash data
对事故数据进行筛选.首先将事故发生前20 min交通流数据中有异常的事故数据进行剔除.其次由于G15布设的线圈检测器并不均匀,当线圈间隔较大时,交通流扰动很难检测到,间隔较小时,所筛选出事故数据样本量较小,预测模型不能得到有效训练,所以筛选上下游检测器间隔在4 km内的事故数据,可以保证交通流数据的有效性,且满足模型样本量要求,共筛选到86起追尾和碰擦事故.
1.2 事故对照数据
为了对比事故发生前和正常状态下的交通流动态特征,交通流数据需要按配对方式选取,采用病例-对照研究方法,其中病例组为交通事故发生前的交通流动态特征,对照组为没有发生事故条件下的交通流动态特征.在交通安全研究领域,病例和对照的比例选择了常用的1∶4[15-16].
非事故数据选取时,应注意与事故数据在相同地点、相同时间、相同季节、不同日期条件下采集得到,控制道路的几何条件、时段等对事故发生的影响.此外,在提取非事故数据时,要确保取样时段前后1 h内没有事故发生,以保证非事故数据能反应正常情况的交通条件.
例如,有一个事故发生在2014年4月9日17:35,将17:15~17:35之间距离事故发生地点最近的检测器数据提取出来,并根据规则,提取3月26日、4月2日和4月16日及4月23日相同时刻的交通流数据.17:30~17:35的数据为0~5 min组,17:25~17:30的数据为5~10 min组,17:20~17:25的数据为10~15 min组,17:15~17:20的数据为15~20 min组.
2 风险预测模型与变量选取
2.1 支持向量机
基于统计学习理论的结构风险最小化原则的SVM方法,将实际问题通过非线性变换转换到高维特征空间,在高维空间中构造线性判别函数来实现原空间中的非线性判别问题,其算法复杂度与样本维数无关[18].并且相比于神经网络,SVM不易陷入局部最优,更适合于小样本情况.基于交通风险预测问题的特点,本文选用支持向量机进行模型构建.
设有n个样本xk及其所属类别yk,表示为(xk,yk),k=1,2,3…N,xk∈RN,N表示输入空间的维度,yk∈{1,-1}.xk指的是第k个样本的交通流参数,yk是该样本所对应的交通状态:如果是导致事故发生的状态,则yk=1,如果是非事故发生状态,yk=-1.本文为非线性分类问题,支持向量机通过核函数,将数据映射到高维空间,使其变为线性可分问题,并在这个特征空间中构造最优分类超平面.最终寻优目标函数为式(1),相应的分类函数式为式(2).
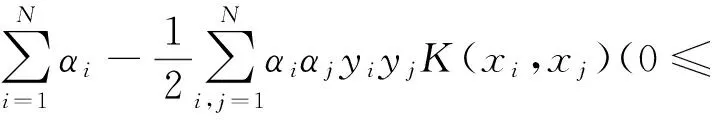
αi≤C)
(1)
(2)
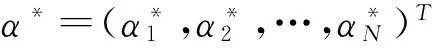
K(xi,xj)=exp(-g||xi-xj||2),g>0
(3)
模型预测精度评价指标一方面是检验SVM模型优良程度的标准,另一方面也是SVM模型参数交叉验证寻优过程的基本依据.模型分类精度采用的统计指标为总体预测精度、事故预测精度和误报率.总体预测精度是指预测正确的样本数占样本总数的比例,事故预测精度是指预测正确的事故样本数占事故样本总数的比例,误报率是指将非事故样本预测为事故样本的数目占非事故样本总数的比例.
2.2 特征变量选取
提取历史事故数据和交通流原始数据,对数据进行集计,以形成一些容易识别出高事故风险交通状态的特征变量.在短期交通流风险预测模型的研究中,国内外学者提出了很多特征变量,如速度标准差、速度变异系数、不同检测器不同时间间隔的速度、流量、占有率数据[15-17].为进一步研究货车比例在短期交通流风险预测中的作用,在特征变量选取中考虑了货车因素.为方便命名和编号,事故上游检测器采集到的参数在第一位用U标明,事故下游检测器采集到的参数在第一位用D标明,特征变量如表1所示.
将交通流运行风险分为可能发生事故和不会发生事故两种状态,因此可以将交通流风险预测问题看成一个二分类问题,样本数据中包含事故数据与非事故数据,每个数据包含A组、B组、C组不同维度的自变量,如果发生事故则将状态变量记为1,未发生事故则将状态变量记为-1.将样本数据分为训练样本样本和测试样本,模型基于训练样本数据对分类器进行训练并建立模型,利用建立的模型对测试数据集进行估计,以此验证模型的精度.
3 模型构建
由于事故样本与非事故样本不均衡,首先对样本进行过抽样,可得到4个时间段,3组特征变量的12个数据组.使用MATLAB平台Libsvm进行SVM建模,由于惩罚参数C和RBF核函数参数g对SVM模型分类会有很大影响,因此,本文采用网格搜索法和遗传算法相结合的方法对参数C和g进行寻优.得到12个SVM分类器模型,对分类器效果进行比较分析,可得到预测效果最佳的时间段及特征变量组.

表1 模型中所用特征变量Tab.1 Characteristic variables used in the model
注:C组综合变量由A组变量与B组变量合并形成
3.1 基于SMOTE算法的过抽样方法
在数据选取时,按照病例对照的方法,事故数据与非事故数据采集的比例为1:4,会出现样本不均衡的问题.为解决非平衡类数据集带来的误分类问题,本文采用SMOTE算法改变数据集的样本分布.SMOTE算法通过人工构造少数类样本来增加正类样本的数量,从而减少数据失衡程度,从而提高模型的预测精度[19].该算法的基本假设为同类别样本在模式空间中必定互相靠近,因此在一个少数类样本最近邻随机选择一个样本,在两者之间的连线上随机选一点作为新合成的少数类样本.若抽样率是m,对于每个少数类样本xi,找出它k个少数类近邻点.从中任选m个近邻点yij(j=1,2,…,m),具体插值方法如下:
Pj=xi+rand(0,1)(yij-xi)
(4)
选取整体交通流特征变量,提取事故前5~10 min交通流数据,通过SMOTE算法将少数类样本扩大不同的倍数,使用2组不同的惩罚因子C和核参数g,构建SVM模型并进行比较分析.为使用同一个分类器模型对不同倍数预测结果进行比较,选取参数时并未使用遗传算法优化参数.结果见表2.
通过表2可知,在未进行SMOTE过抽样时,事故预测精度均为0.经过SMOTE算法过抽样后,尽管模型参数选择不同,但事故预测精度均得到提升.对比将事故数据扩大2倍和4倍的结果,扩大4倍后,事故样本与非事故样本同样多,不存在数据不均衡性问题,误报率有所降低,但事故预测精度有较大提高.因此,最终选择将少数类样本扩大4倍,并对模型参数进行寻优.
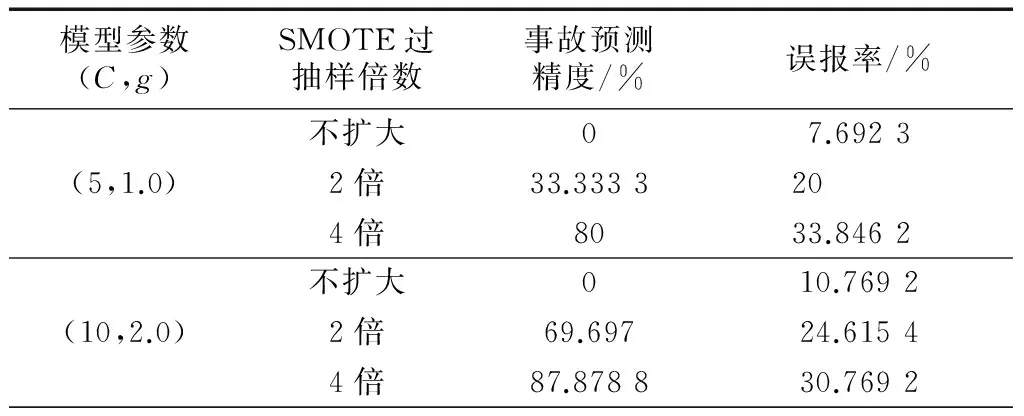
表2 不同扩大倍数的预测精度Tab.2 The prediction accuracy of different multiples
3.2 基于遗传算法的SVM参数寻优
采用的核函数是径向基核函数,主要的参数是惩罚因子C和核参数g.参数C表明了对误差的宽容度,C越大,容忍出错的程度越小;参数g是核函数半径,隐含地决定了数据映射到新的特征空间后的分布.提高SVM模型的分类精度就要选择合适的方法对模型参数进行选择.遗传算法属于启发式算法,鲁棒性较强,对函数要求不高,且不容易陷入局部最优[20],因此,采用遗传算法对SVM模型参数进行选择.在用遗传算法对参数进行寻优时,首先要对参数的寻优范围进行设置.采用网格搜索法对模型参数进行粗选,确定参数的大致范围,再用遗传算法对参数进行精选.以C组变量为例,首先将参数C、g设置为默认值,粗选结果如图2所示.

图2 参数C和g网格搜索法粗选结果Fig.2 Rough selecting results of parameters usinggrid search method
由图2可知,预测的分类精度最高为88%左右,综合考虑寻优的复杂度及参数寻优质量,得到参数的粗选结果为C∈[2-1,25],g∈[20,26].得到参数粗选结果后,采用遗传算法对参数进行精选.对参数进行二进制编码,并将种群初始化,为降低算法的复杂度,初始种群规模不宜太大,因此本文将种群中个体数目定为20个.采用k-折交叉验证(k-fold cross validation)的方法来评价SVM分类模型的性能.k-折交叉验证将原始样本分成k个互不相交的子集,即k-折.然后将每个子集数据分别做一次验证集,其余的k-1组子集数据作为训练集,最终,将会得到k个模型分类精度A1,A2,…,Ak.用这k个分类精度的平均数A作为k-折交叉验证下的性能指标,即
(5)
由于遗传算法是随机搜索算法,迭代终止条件并没有统一的方法.一般采用达到预先设定的代数作为遗传算法迭代终止条件,将迭代次数设为100,迭代终止后选择最优适应度值作为最后的解.在运算过程中,可能会有多组的C和g对应于最高的验证分类准确率,由于惩罚参数C取值过大时会造成“过学习”状态的发生,即训练集分类准确率很高而测试集分类准确率很低,使构建的SVM模型泛化能力降低.因此,在处理这种情况时,优先选择参数C最小的那组C和g作为最佳参数,如果参数C最小时对应多组参数g,则选取搜索到的第1组C和g作为最佳参数.
3.3 预测结果及分析
以5 min为时间间隔选择事故发生前20 min的特征变量,用遗传算法对模型参数进行寻优,共建立了12个SVM分类器,进行多次迭代,如图3所示,为C组变量迭代的一组实例.
将遗传算法迭代运算后求得的参数组合对训练数据集进行训练,可获得较高预测精度.将模型应用于测试集,可得到最终的分类预测结果如表3所示.
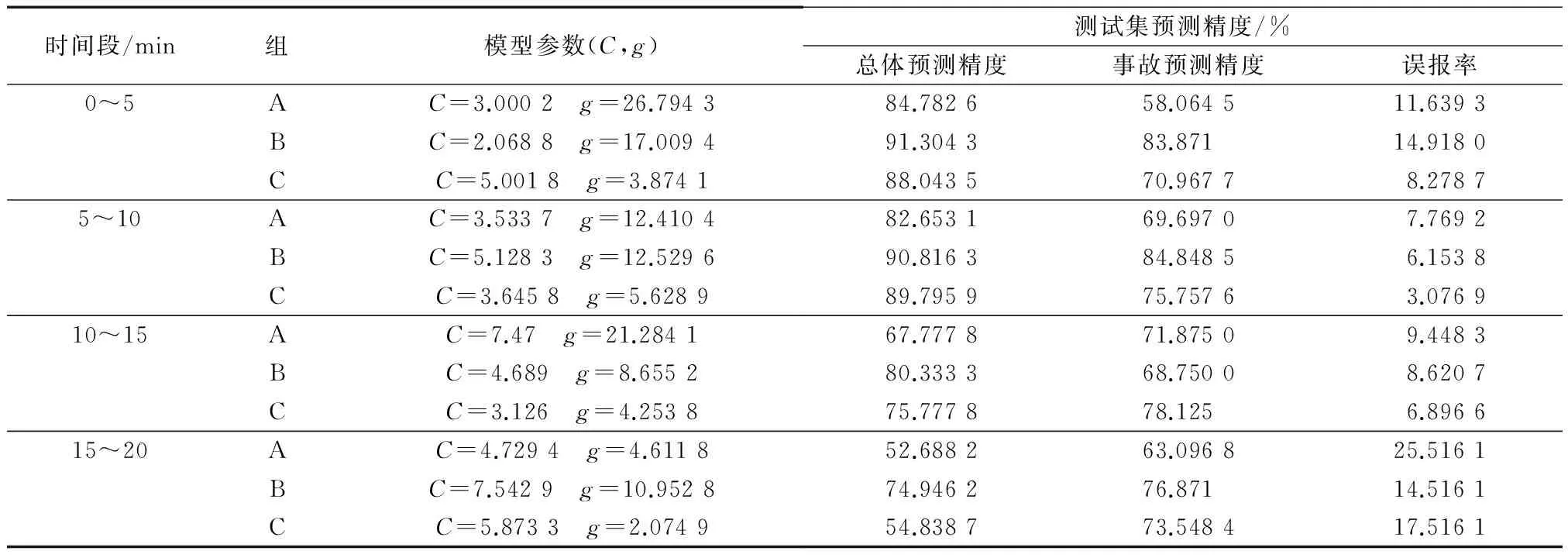
表3 各组模型参数及预测精度Tab.3 Parameters and prediction accuracy of models
首先比较不同时间段之间的预测精度.从表中看出,事故发生前15~20 min、10~15 min的总体预测精度、事故预测精度相比于0~5 min,5~10 min低,而误报率较高,表明距离事故发生时间较早的交通流数据提供的可用于预测事故的信息量较少,对于交通流风险预测的价值较低.而本文将事故接警时间等同于事故发生时间,实际事故发生时间要更早,尽管此处的0~5 min时段具有较好的总体预测精度,但此时段可能包含事故发生后的数据.另外考虑到在实际交通流风险预测的应用中,预测时间应保证一定的提前量,即应当给交通管理部门一定的反应时间来采取措施,因此0~5 min时段不作为预测时间段.综上,5~10 min时段的预测效果更好.
将3组特征变量事故发生前5~10 min的预测结果进行比较,结果发现:与A组变量相比,C组变量总体预测精度与事故预测精度均得到提高,且误差率降低至3.076 9%,说明加入货车相关变量,可提高交通流风险预测精度.B组变量即仅采用货车特征变量时,总体预测精度和事故预测精度相比于C组有所提高,但误报率有所升高.B组和C组变量均比A组变量有更好的预测效果,即本路段在进行交通流风险预测时,应当将货车变量作为风险特征变量.
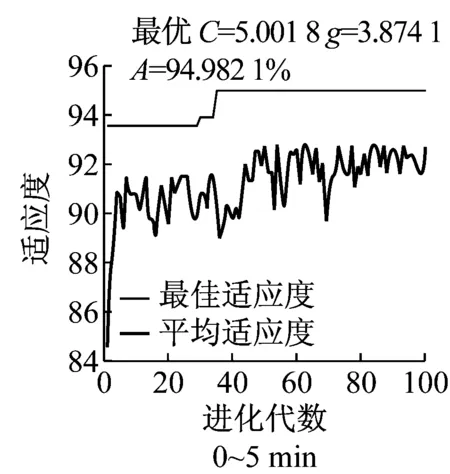
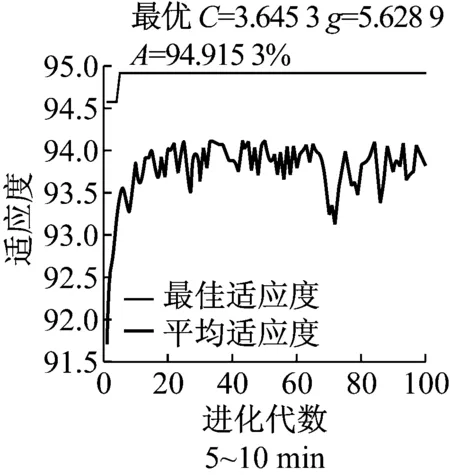
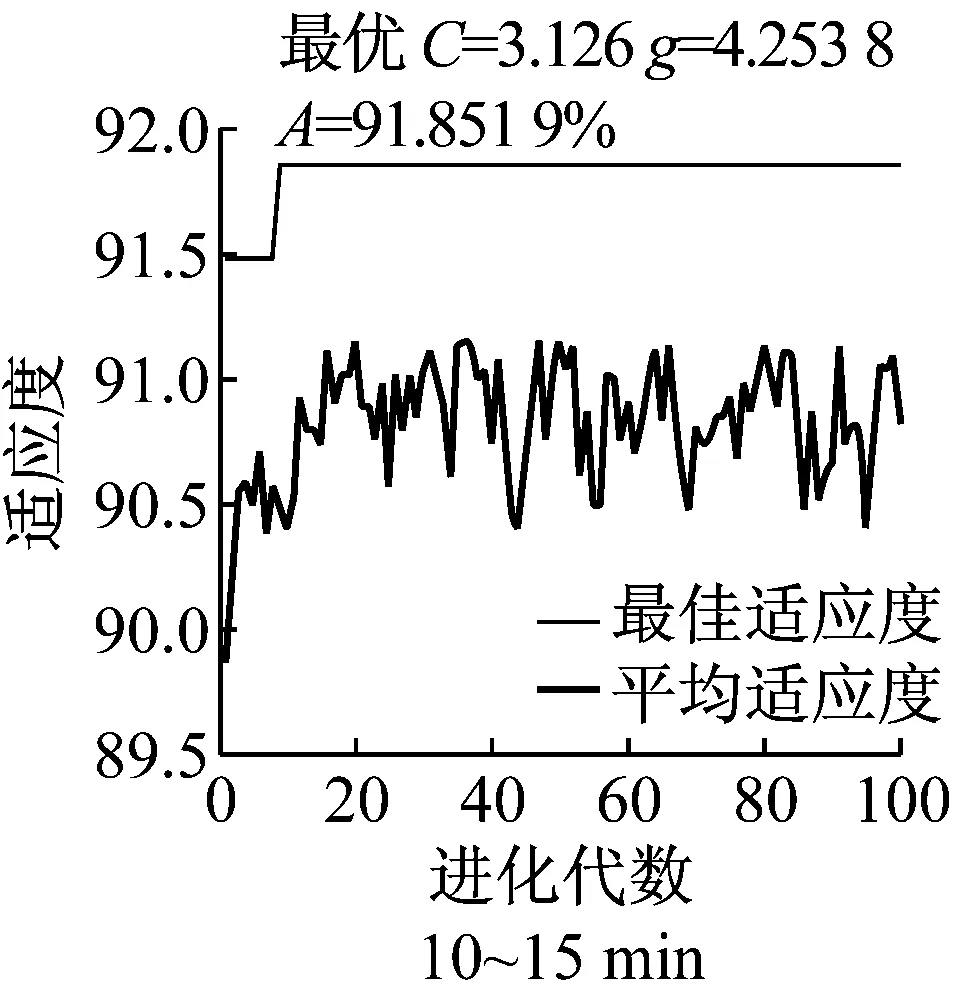
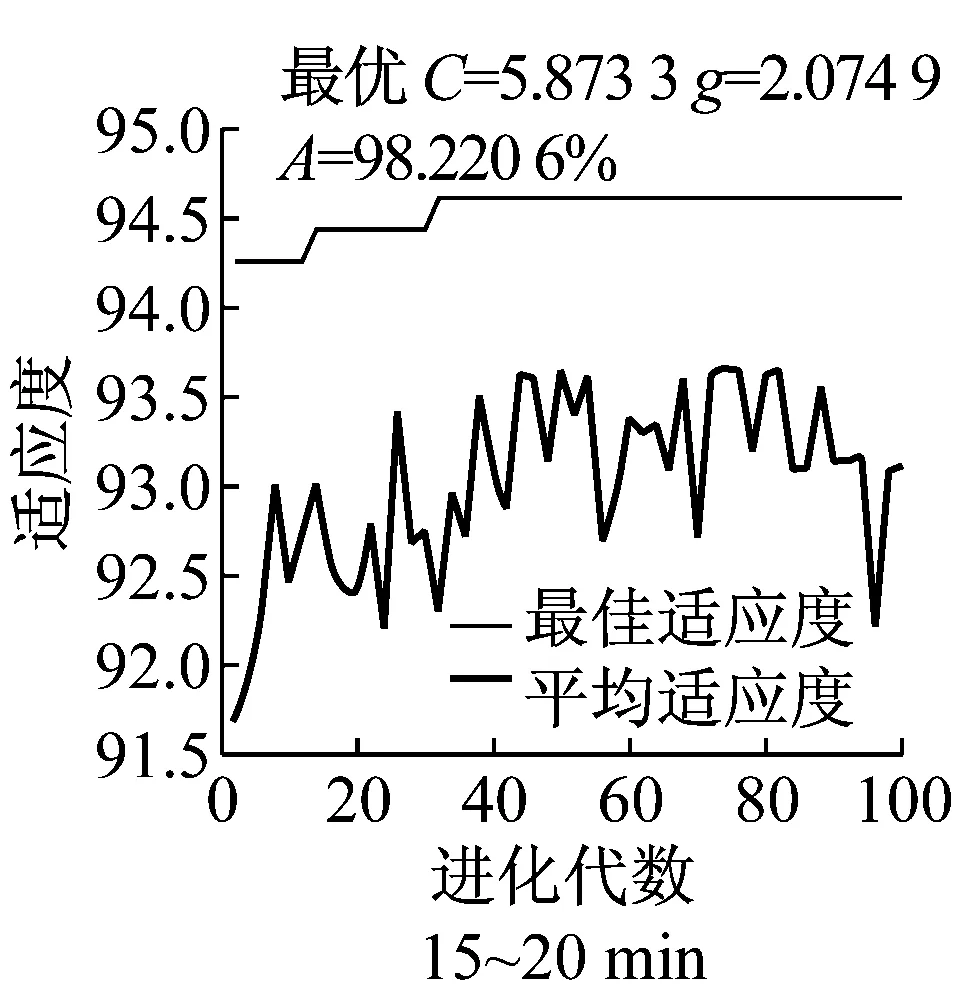
图3 SVM模型参数寻优图Fig.3 parameter optimization of SVM models
3.4 基于MIV值的敏感性分析
考虑到模型中风险特征变量较多,因此采用平均影响值法(MIV法)研究在C组变量中,货车因素对预测结果的影响程度,同时对特征变量进行分析和筛选.MIV方法在神经网络中是非常有效的一种变量筛选方法,在模型训练终止后,将训练样本中每一特征变量在其原值的基础上分别加减10%构成两个新的训练样本,再利用已建成的模型得到两个新的结果,新结果之间的差值即为变动该特征变量对预测结果产生的影响变化值.结合前文中对所建立的SVM预测模型的比较,选择事故发生前5~10 min的C组特征变量的预测模型,计算各特征变量的MIV值,取绝对值后进行排序,得到的结果如表4所示.
在30个特征变量的前10个主要影响变量中,下游占有率标准差对预测模型的影响最大,即当下游占有率发生变化时,由于交通流的传递性,上游交
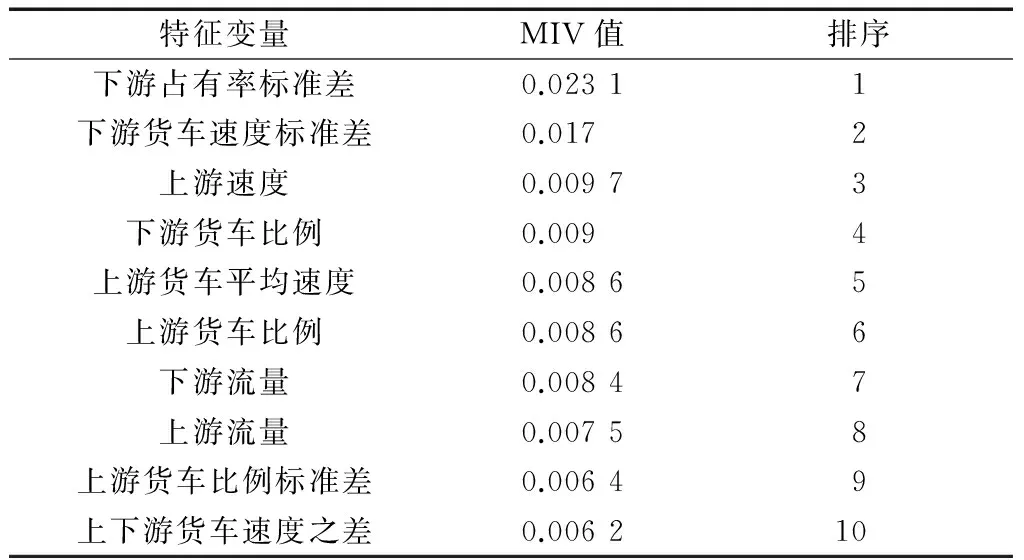
表4 C组变量模型的MIV值统计表Tab.4 Statistical table of MIV values of Group C model
通流受到干扰,从而增大事故发生的可能性.MIV值排序第2的变量为下游货车速度标准差,即下游货车速度变化值对交通流有较大影响,此结论与Oh等学者[9]研究结论一致,只是其研究中并未对客货车进行区分.可以看到,在前10个主要特征变量中,有6个为货车相关变量,而且上、下游货车比例均在其中,表明在模型中考虑货车相关变量可以提高预测准确率.在货车比例及货车事故率较高路段进行主动安全管理时,应当加强对货车速度以及货车比例的等因素实时监控,从而提高预测的可靠性.
4 结语
将交通流风险预测问题看成一个二分类问题,基于支持向量机,建立了高速公路交通流风险预测模型.分别选取断面整体交通流参数、货车交通流参数和综合参数作为风险特征变量,以5 min为间隔选择事故发生前20 min的特征变量,用遗传算法对模型参数进行寻优.结果表明事故发生前5~10 min的模型预测精度最高,加入货车因素的预测模型比仅考虑交通流参数的模型精度更高,因此可用货车交通流参数作为预测模型的特征变量.在综合变量预测模型中,采用平均影响值法进行分析,结果表明货车因素对于预测模型有较大影响.该模型可用来开发交通安全预警系统,为高速公路安全运营管理提供依据.但由于仅为G15上海段建立了模型,接下来研究应在搜集不同道路条件以及不同货车比例的基础上进行模型优化,提高模型适用性.
参考文献:
[1] 中华人民共和国公安部交通管理局.部分货车车型违规生产问题突出,货车运输安全隐患严重[EB/OL]. [2017-05-03]. http://www.mps.gov.cn/n2255040/n2255043/c5609936/content.html.
Traffic Management Bureau of the Public Security Ministry of the People’s Republic of China. Some trucks have severe problems of illegal production, and the security problem of trucking is serious[EB/OL]. [2017-05-03]. http://www.mps.gov.cn/n2255040/n2255043/c5609936/content.html.
[2] GAZIS D C,HERMAN R. The moving and “phantom” bottleneck [J]. Transportation Science,1992,26(3):223.
[3] MIDDLETON D,VENGLAR S,QUIROGA C,etal. Strategies for separating trucks from passenger vehicles:final report [R]. Texas:Texas Transportation Institute, 2006.
[4] VADLAMANI S,CHEN E,AHN S,etal. Identifying large truck hot spots using crash counts and PDOEs[J]. Journal of Transportation Engineering, 2011, 137 (1) :11.
[5] YANG D,JIN P,PU Y,etal. Stability analysis of the mixed traffic flow of cars and trucks using heterogeneous optimal velocity car-following model [J]. Physica A:Statistical Mechanics and Its Applications, 2014,395(4):371.
[6] ZOU W,WANG X,ZHANG D. Truck crash severity in New York city: an investigation of the spatial and the time of day effects[J]. Accident Analysis & Prevention, 2017,99:249.
[7] NAIK B,TUNG L W,ZHAO S. Weather impacts on single-vehicle truck crash injury severity[J]. Journal of Safety Research,2016,58:57.
[8] OSMAN M,PALETI R,MISHRA S,etal. Analysis of injury severity of large truck crashes in work zones[J]. Accident Analysis & Prevention,2016,97:261.
[9] OH C,OH J S,RITCHIE S G,etal. Real-time estimation of freeway accident likelihood [C/CD]//80th Annual Meeting of the Transportation Research Board. Washington D C: Transportation Research Board, 2001.
[10] ABDEL-ATY M,PANDE A. Classification of real-time traffic speed patterns to predict crashes on freeways[C/CD]//83rd Annual Meeting of the Transportation Research Board. Washington D C:Transportation Research Board, 2004.
[11] PANDE A,ABDEL-ATY M. Comprehensive analysis of relationship between real-time traffic surveillance data and rear-end crashes on freeways [J]. Transportation Research Record:Journal of the Transportation Research Board, 2006, 1953(1):31.
[12] PANDE A,ABDEL-ATY M. Assessment of freeway traffic parameters leading to lane-change related collisions [J]. Accident Analysis & Prevention, 2006, 38(5): 936.
[13] YU R,ABDEL-ATY M. Utilizing support vector machine in real-time crash risk evaluation[J]. Accident Analysis & Prevention,2013,51(2):252.
[14] 孙剑,孙杰. 城市快速路实时交通流运行安全主动风险评估[J].同济大学学报(自然科学版),2014,42(6):873.
SUN Jian,SUN Jie. Proactive assessment of real-time traffic flow accident risk on urban expressway[J]. Journal of Tongji University: Natural Science,2014, 42(6):873.
[15] ABDEL-ATY M, UDDIN N, PANDE A,etal. Predicting freeway crashes based on loop detector data using matched case-control logistic regression [J]. Transportation Research Record: Journal of the Transportation Research Board, 2004, 1897(1): 88.
[16] ABDEL-ATY M, UDDIN N, PANDE A. Split models for predicting multivehicle crashes during high-speed and low-speed operating conditions on freeways[J]. Transportation Research Record: Journal of the Transportation Research Board, 2005,1908(1): 51.
[17] 徐铖铖,刘攀,王炜,等. 恶劣天气下高速公路实时事故风险预测模型[J].吉林大学学报(工学版),2013,43(1):68.
XU Chengcheng,LIU Pan,WANG Wei,etal. Real time crash risk prediction model on freeways under nasty weather conditions[J]. Journal of Jilin University(Engineering and Technology Edition), 2013,43(1):68.
[18] VAPNIK V N. 统计学习理论[M]. 许建华,张学工,译.北京:电子工业出版社,2004.
VAPNIK V N. Statistical learning theory [M]. Translated by XU Jianhua, ZHANG Xuegong. Beijing: Publishing House of Electronics Industry,2004.
[19] CHAWLA N V,BOWYER K W,HALL L O,etal. Smote:synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2011,16(1): 321.
[20] 付阳,李昆仑. 支持向量机模型参数选择方法综述[J]. 电脑知识与技术,2010,6(28):8080.
FU Yang,LI Kunlun. A survey of model parameters selection method for support vector machines [J]. Computer Knowledge and Technology,2010,6(28):8080.

